SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC

Andr´e Lourenc¸o

1,2

and Ana Fred

Instituto Superior de Engenharia de Lisboa, Lisboa, Portugal

Instituto de Telecomunicac¸˜oes, Instituto Superior T´ecnico, Lisboa, Portugal

Keywords:

Cluster analysis, Evidence accumulation clustering (EAC), Multiple-criteria evidence accumulation clustering

(Multi-EAC).

Abstract:

The Multiple-Criteria Evidence Accumulation Clustering (Multi-EAC) method, is a clustering ensemble ap-

proach with an integrated cluster stability criterion used to selectively learn the similarity from a collection

of different clustering algorithms. In this work we analyze the original Multi-EAC criterion in the context of

the classical relative validation criteria, and propose alternative cluster validation indices for the selection of

clusters based on pairwise similarities. Taking several clustering ensemble construction strategies as context,

we compare the adequacy of each criterion and provide guidelines for its application. Experimental results on

benchmark data sets show the proposed concepts.

1 INTRODUCTION

A recent trend in clustering, that constitutes the state-

of-the art in the area, are clustering combination

techniques (also called clustering ensemble methods)

(Fred, 2001; Fred and Jain, 2005; Strehl and Ghosh,

2002; Fern and Brodley, 2004; Topchy et al., 2005;

Ayad and Kamel, 2008). These methods attempt to

ﬁnd better and more robust partitioning of the data by

combining the information of a set of N different par-

titions, the clustering ensemble - P.

In (Fred and Jain, 2006) the authors proposed

the Multi-Criteria Evidence Accumulation Cluster-

ing (Multi-EAC) method as an extension to the EAC

framework (Fred, 2001; Fred and Jain, 2005), ﬁlter-

ing the cluster combination process using a cluster

stability criterion. Instead of using the information

of the different partitions, it is assumed that, since

algorithms can have different levels of performance

in different regions of the space, only certain clusters

should be considered. This algorithm selectively de-

cides on the expertise level of each algorithm over the

several regions of the space, highest local expertise

overriding less conﬁdent decisions, and low exper-

tise decisions being totally ignored in the combination

process.

In this paper we focus on the shift of paradigm -

from partition to cluster level validation. We propose

to further explore the stability criteria proposed in the

framework of the Multi-EAC, contextualizing it on

the classical relative validation criteria.

Using this motivation we propose some cluster

validation criteria, which validate each of the clusters

in a data partition. With the proposed criteria we go

beyond the classical problem of partition validation,

focusing our goal in evaluating the quality of individ-

ual clusters. Furthermore we adapt these criteria to

pairwise similarities, evaluating them in the context

of the Multi-EAC algorithm.

The remainder of this document is organized as

follows. In the next section we review the classi-

cal clustering validity criteria used to assess the qual-

ity of partitions relative to each other, contextualizing

the present work on previous works. In section 3 we

brieﬂy review the clustering combination techniques

and the Multi-EAC paradigm. We propose new cri-

teria for cluster validation, in section 4, shifting the

paradigm from partition to individual cluster analy-

sis. The proposed formulation is based on pairwise

similarities instead of feature-based object represen-

tations. In section 5 we apply the proposed indices

in the context of Multi-EAC method. In section 6 we

present the experimental setup and results over bench-

mark and real data-sets. Finally in section 7 we draw

some conclusions and present future work.

491

Lourenço A. and Fred A..

SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC.

DOI: 10.5220/0003099904910499

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 491-499

ISBN: 978-989-8425-28-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

The problem of evaluation/comparison of clustering

results as well as deciding the number of clusters bet-

ter ﬁtting the data is fundamental in cluster analysis

and it has been subject of many research studies (Jain

and Dubes, 1988; Dubes and Jain, 1979; Levine and

Domany, 2000; Halkidi et al., 2002a; Halkidi et al.,

2002b; Verma and Meila, 2003).

In the literature there are various methods for

quantitative evaluation of clustering results known

under the name of clustering validation or evaluation

techniques. Measures or indices of cluster validity are

classically divided into three types: A) External; B)

Internal; C) Relative. For more details consult (Jain

and Dubes, 1988; Sergios Theodoridis, 1999; Halkidi

et al., 2002a).

In this paper we evaluate the clustering structure,

focusing on Relative criteria and cross-validation.

The basic idea of Relative criteria is the evalu-

ation of the clustering structure by comparing it to

other clustering schemes, resulting from the same

algorithm but with different parameter values, or

from other algorithms. Many different indices have

been proposed in the literature, such as the Silhou-

ette (Rousseeuw, 1987), Dunn’s Index, Davies and

Bouldin (Jain and Dubes, 1988) (Halkidi et al., 2001).

Most of them are geometrical motivated and estimate

how compact and well separated the clusters are.

Our approach builds over this indices but instead

of validating all the partition, we consider each cluster

independently.

Other approaches to clustering validation include

variants of cross-validation (Jain and Moreau, 1987;

Levineand Domany, 2000; Ben-Hur et al., 2002; Roth

et al., 2002), where, unlike classical cross-validation

(used in supervised classiﬁcation), no class informa-

tion is required. Several related procedures have also

been proposed for inferring the number of clusters

(Lange et al., 2002). These techniques focus on an-

alyzing the stability of the solution and can be cat-

egorized in the internal validity criteria for clustering

validation, not requiring any kind of a priori informa-

tion. Methods adopting this approach use different re-

sampling schemes to simulate perturbations over the

original data-set, so as to assess the stability of the

clustering results with respect to sampling variability.

Partitioning results that are more robust (i.e., with mi-

nor cluster assignment changes) with respect to the

data perturbation are chosen as the most consistent

and better solutions.

The Multi-EAC uses this last class of techniques,

using sub-sampling to assess the stability of pairwise

co-associations.

3 CLUSTERING ENSEMBLE

METHODS AND MULTI-EAC

Clustering ensemble methods can be decomposed

into a cluster generation mechanism and a partition

integration process, both inﬂuencing the quality of

the combination results. Different approaches have

been followed for the production of the clustering en-

semble, involving different proximity measures, al-

gorithms, initializations, and features spaces. For

the combination process there are also diverse ap-

proaches, from graph-based (Strehl and Ghosh, 2002;

Fern and Brodley, 2004), voting or statistical perspec-

tives (Fred, 2001; Fred and Jain, 2005; Topchy et al.,

2005; Ayad and Kamel, 2008). Overall, the several

methods equally weight clusters belonging to an in-

dividual partition, as schematically plotted in ﬁgure

Figure 1: Schematic description of a clustering ensemble

method.

Fred and Jain (Fred and Jain, 2005; Fred, 2001)

proposed a statistical method of combination, the Ev-

idence Accumulation Clustering (EAC), based on co-

occurrences of pairs of objects in the same clusters,

which can be interpreted as pairwise votes, over the N

different partitions of the clustering ensemble. This is

a robust combination method that additionally to the

combined partition, P

∗

, produces as intermediate re-

sult a learned pairwise similarity, summarizing max-

imum likelihood estimates of pairwise co-occurence

probabilities, as assessed from the clustering ensem-

ble (see ﬁgure 2).

In (Fred and Jain, 2006) the authors proposed

Multi-Criteria Evidence Accumulation Clustering

(Multi-EAC) method as an extension of the EAC

framework, ﬁltering the cluster combination process

(see ﬁgure 3) using a cluster stability criterion. In-

stead of using all the pairwise co-associations, it is

assumed that, since algorithms can have different lev-

els of performance in different regions of the space,

only certain pairwise co-associations should be con-

sidered. Its selection is assessed through a stability

criterion based on subsampling.

The method relies on two stages: the ﬁrst stage

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

492

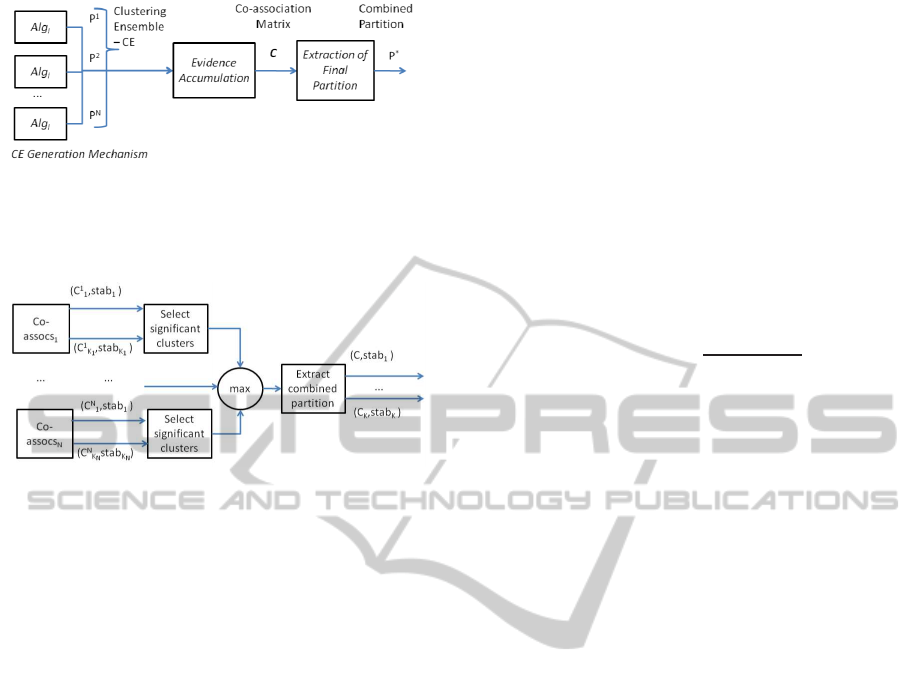
Figure 2: The main phases in the EAC method. The

data partitions of the Clustering Ensemble (CE) are com-

bined accumulating the pairwise co-associations over the

co-association matrix, C .

Figure 3: Evidence Accumulation under the Multi-EAC

framework: ﬁltering the cluster combination process.

aims at learning, for each algorithm, what are the re-

gions where it performs well, that is, it selective learns

clusters based on a sub-sampling and ensemble com-

bination approach; the second stage integrates this in-

formation, combining the selected clusters.

Lets us deﬁne clustering algorithm instantiation

the tuple formed by a clustering algorithm and a par-

ticular instantiation of the corresponding algorithmic

parameters. Hereafter, for simplicity, we refer by al-

gorithm l, denoted by Alg

, one such clustering algo-

rithm instantiation.

The identiﬁcation of the regions where a partic-

ular algorithm, Alg

, performs well is based on sta-

bility analysis over combination results obtained by

applying the EAC method (Fred and Jain, 2005) on

perturbed versions of the data-set, obtained through

sub-sampling.

Let X = {x

,...,x

} represent a data-set with

observations, and X

sub

be a sub-sampling version

of the data set, by randomly selecting (without repo-

sition) b samples from X, (b < n

). In total, there are





different sub-sampling versions of the data-set.

Each X

sub

is clustered using Alg

, yielding the

partition P

. Given N such perturbed versions of the

data set, through algorithm Alg

we obtain a cluster-

ing ensemble CE

. These partitions are combined us-

ing the EAC method, accumulating the pairwise evi-

dence over the co-association matrix, C

, whose en-

tries are deﬁned by:

(i, j) = n

, (1)

where n

is the number of co-associations of the pair

(i, j), and m

the number of subsampling experiments

where this pair is present. Note that the subscript l

indicates that this matrix was obtained according to

algorithm Alg

. For extracting clusters obtained by

this algorithm, any clustering algorithm that accepts

a similarity matrix (the co-association matrix) as in-

put can be applied. Typically the Single Link or Av-

erage Link agglomerative hierarchical methods (Jain

and Dubes, 1988) are used.

In order to identify the different levels of local per-

formance of the algorithm, the stability of each of the

extracted cluster is computed using the co-association

values of that cluster (denoted by C

), according to:

stab

∑

i, j∈C

, j6=i

C (i, j)

)(n

− 1)

, (2)

where n

is the number of objects in C

, correspond-

ing to average pairwise stability of cluster C

Only clusters having stability values higher than a

speciﬁed threshold, th, are selected; thus the method

selectively learns pairwise similarities, over each en-

semble, that is over each Alg

In the second stage of the algorithm, the selected

clusters are further combined into a global similarity

matrix using a max rule. Each selected cluster, repre-

sented in a n

× n

co-association matrix, is combined

with the other clusters selecting the sub-matrices with

more stable values (max rule), thus joining all the in-

dividual contributions.

4 THE PROPOSED

FRAMEWORK:

CLUSTER VS PARTITION

VALIDITY CRITERIA

While classical validity indexes are designed to mea-

sure the overall quality of data partitions, our goal is

to deﬁne indices that measure the quality of individual

clusters within a partition, and amongst distinct par-

titions. Herein we propose several indices to address

this problem reviewing ﬁrst the classical ones.

Most of the relative indices use geometrical con-

siderations, and are based on a dissimilarity matrix

computed over the original feature space, such as the

Euclidean distance. Let d(i, j) represent the dissimi-

larity between objects i and j.

The Silhouette index(Rousseeuw, 1987) judges

the quality of a clustering solution by quantifying the

compactness/separability of clusters. For each object

in a cluster, the ”Silhouette value”, measures the de-

gree to which a sample belongs to its current cluster

SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC

493

relative to the other K-1 clusters. For each, x

∈ C

, let

a(i) denote the average distance between the object

and all other objects in C

, and b(i) denote the aver-

age distance between x

and all objects in the nearest

competing cluster C

a(i) =

| − 1

∑

j∈C

,i6= j

d(i, j) (3)

b(i) = min

b6=i

(

∑

j∈C

d(i, j)

)

(4)

The silhouette width for each x

is computed us-

ing:

s(i) =

b(i) − a(i)

max{a(i),b(i)}

(5)

A global silhouette width can be computed taking

the mean of the silhouette width for all samples in the

data-set:

S =

∑

i=1

s(i) (6)

To measure the compactness of a cluster, C

, we

propose to measure the average dissimilarity of the

pairs of samples within that cluster:

)(n

− 1)

∑

i, j∈C

, j>i

d(i, j) (7)

To measure the separability between C

and its

nearest cluster C

, we compute the average dissimi-

larity between pairs of objects in C

and the objects in

the competing cluster C

= min

1≤l≤K , l6=k

)(n

)

∑

i∈C

∑

j∈C

d(i, j) (8)

We deﬁne the Cluster Silhouette (Bolshakova

and Azuaje, 2003), as:

− A

max{A

}

(9)

This produces a score in the range [−1,1], indicat-

ing how good an individual cluster is within its par-

tition. A value close to 1 indicates that the cluster is

compact and separated from the other clusters; a value

closer to 0 suggest that the cluster is not so compact or

separated from the nearest clusters, while a negative

value suggest that is likely that the clusters has been

incorrectly assigned.

Dunn’s index (Dunn, 1974) (Bezdek and Pal,

1995) quantiﬁes how compact and well separated

clusters are, being deﬁned as:

D = min

1≤q≤K



min

q+1≤r≤K



dist(C

)

max

1≤p≤K

diam(C

)



(10)

where dist(C

) represents the distance between

the q-th and the r-th cluster, and diam(C

) is the p-

th cluster diameter, as deﬁned by:

dist(C

) = min

i∈C

, j∈C

d(i, j), (11)

diam(C

) = max

i, j∈C

d(i, j), (12)

In order to compare different clusters we propose

to compute the Dunn’s cluster index, for cluster C

which can be deﬁned as:

min

1≤r≤K,r6=k

dist(C

)

diam(C

)

(13)

This validation index can be used to compare dif-

ferent clusters and if D

> 1 this is indicative that the

cluster C

is compact and separated from the other

clusters.

5 CLUSTER SELECTION

CRITERIA IN MULTI-EAC

The Multi-EAC algorithm relies on the identiﬁcation

of clusters selected from the extracted solutions of

the ensembles produced by the different algorithms,

based on co-association values, C . In (Fred and Jain,

2006) the selection of clusters was performed accord-

ing to equation 2. The idea behind this test is to mea-

sure the mean evidence of co-association of pairs of

samples over the subsampling experiments performed

over the data-set, using one particular algorithm. If

pairs of samples have been co-associated by the clus-

tering algorithm over these subsampling versions of

the data-set, then these samples should be selected as

stable associations. This value can be interpreted as

an intra-cluster stability criteria, since only samples

belonging to the same cluster are used. We will refor-

mulate the previous index in the context of the cluster

validity criteria.

In previous section, indexes are deﬁned based on

dissimilarities, the following are adaptations using the

similarities represented in the co-association matrix

C .

To measure the compactness of a cluster C

, the

term (equation 7) can be reformulated, using the

intra-cluster similarity, as:

)(n

− 1)

∑

i, j∈C

, j>i

C (i, j) (14)

To quantify the separability between clusters, the

term (equation 8), can be reformulated with the

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

494

inter-cluster similarity, measured by the maximum

similarity between clusters:

= max

1≤l≤K , l6=k

)(n

)

∑

i∈C

∑

j∈C

C (i, j) (15)

Notice that, when using sub-sampling for produc-

ing clustering ensembles, the co-association matrix,

C , represents both pairwise similarity and pairwise

stability, due to the perturbation on the data set. In

this later situation, the intra-cluster similarity given by

equation 14 corresponds to the previously proposed

cluster stability validity index, stab

, as in equation

Both A

and B

vary in the range [0,1] (since

C (i, j) is in the interval [0, 1]) indicating for the up-

per limit of the interval, high intra-cluster similarity,

and high inter-cluster similarity.

To integrate both the intra-cluster and the inter-

cluster information, we reformulate the Cluster Sil-

houette (in equation 9) as:

− B

max{A

}

(16)

Notice that in this case we would like to have a

intra-cluster value (A

) larger than the inter-cluster

similarity (B

), and therefore the numerator is rede-

ﬁned in reverse order. S

takes values the same in-

terval [-1,1], following the indications of the previous

deﬁned S

: values close to 1 indicate that cluster C

compact and well separated.

The second proposed index is a reformulation of

the Dunn’s cluster index (equation 13) using similar-

ities:

diam(C

)

max

1≤r≤K,r6=k

sim(C

)

(17)

where sim(C

) represents the similarity between

the k-th and the r-th cluster, and diam(C

) is the k-th

cluster diameter, deﬁned in terms of pairwise similar-

ities by:

sim(C

) = max

i∈C

, j∈C

C (i, j) (18)

diam(C

) = min

i, j∈C

C (i, j) (19)

Both diam(C

) and sim(C

) vary in the range

[0,1] (since C (i, j) is in the interval [0, 1]) indicating

for the upper limit of the interval, high intra-cluster

similarity, and high inter-cluster similarity.

Notice in the deﬁnition of D

, the numerator and

the denominator are exchanged (compared with equa-

tion 13), allowing that when D

> 1 is also an indica-

tion of compact and well separated cluster.

We propose to evaluate the efﬁciency of the pre-

vious measures for the selection of the clusters in the

Multi-EAC Algorithm. We compare the selection of

clusters using the intra-cluster and the inter-cluster

pairwise similarity in order to determine whichcluster

should be selected. Clusters with high value of intra-

cluster similarity should be considered; clusters with

inter-cluster similarity lower than a given threshold

th can also be considered well separated. Moreover,

we study the integration of both concepts (intra and

inter-cluster similarities), using the Cluster Silhouette

and the Dunn’s cluster index, trying to improve the

robustness of the selection.

In the rest of the paper consider the following no-

tation:

intrasum: The original selection index used as base-

line quality measure - uses the intra-cluster aver-

age similarity (equation 14). Cluster selection cri-

terion: intrasum > th

intrasum

;

intersum: Uses the inter-cluster average similarity

(equation 15). Selection criterion: intersum < th

⇔ (1− intersum) > th

intersum

;

silh: Global silhouette of a cluster (equation 16). Se-

lection criterion: silh > th

silh

;

intramin: Computes the minimum intra-cluster sim-

ilarity, related to cluster diameter, according to 19.

Selection criterion: intramin > th

intramin

;

intermax: Computes the maximum inter-cluster

similarity, according to 18. Selection criterion:

intermax < th ⇔ (1 − intermax) > th

intermax

;

Dunn: Dunn’s cluster index, according to 17. Selec-

tion criterion: Dunn > th

Dunn

The selection of clusters depends on the com-

parison with pre-determined thresholds. To select

compact and well separated clusters, in the case of

intrasum

, th

intersum

, th

intramin

and th

intermin

the thresh-

old should be close to 1; in the case of the th

Dunn

the

threshold should be higher that 1.

The estimation of the most adequate threshold is

out of the scope of the present paper. In this paper we

ﬁxed th

Dunn

= 10 and the remaining thresholds were

set to th = 0.9.

6 EXPERIMENTAL ANALYSIS

We base our evaluation of the proposed criteria on

several synthetic and real-world benchmark data-sets

from the UCI repository (Asuncion and Newman,

2007).

To produce the ensembles we use different algo-

rithms, enabling the selection of clusters based on

different clustering criteria: three agglomerative hi-

erarchical clustering methods (Jain and Dubes, 1988)-

SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC

495

Single Link, Complete Link, Average Link (either ﬁx-

ing the number of clusters or using the life-time cri-

teria (Fred and Jain, 2005)); one partitional cluster-

ing method - K-means (Jain and Dubes, 1988); and a

Spectral Graph Partioning Algorithm - NJW Spectral

Clustering (Ng et al., 2002).

In table 1 we present the data-set characteristics

and the parameter values used with different cluster-

ing algorithms. For the NJW Spectral Clustering, the

scaling parameter σ in the Gaussian afﬁnity matrix,

representing the similarity matrix, was taken in the

intervals σ

= [0.08,0.1 : 0.05 : 0.95,1 : .5 : 10], σ

[0.08, 0.1 : 0.1 : 0.9,1 : 1 : 10] and σ

= [1 : 0.5 : 10],

where [σ

min

: inc : σ

max

], represents the set of all σ

values beginning with σ

min

, terminating with σ

max

with increments of inc.

Table 1: Benchmark data-sets characteristics and parameter

values used with different clustering algorithms.

Data-Sets K n

Ensemble

Ks σ

spiral 2 200 2-8 σ

cigar 4 250 2-8 σ

rings 3 450 2-6 σ

breast-cancer 2 683 2-10,15,20 σ

iris 3 150 3-10,15,20 σ

image-1-Martin 7 1000 7-15,20,30, 37 σ

We applied each clustering algorithm instantia-

tion, Alg

(characterized by a set of parameter values),

to N different subsampled versions, X

sub

, of the data-

set, ﬁxing N=100. The obtained clustering ensemble

is combined over the co-association matrix C

For extracting the combined partitions, we used the

Single Link and the Average Link agglomerativehier-

archical methods, ﬁxing the number of clusters equal

to the real number of clusters, and using the life-time

criteria (Fred and Jain, 2005).

We applied each of the stability criteria to the ex-

tracted solutions. We selected a cluster when its sta-

bility was higher than a given threshold. The applied

thresholds were th = 0.9 for intrasum, silh, intramin,

1-intramax, 1-intersum. For the Dunn we selected

th = 10.

The accuracy of the results is evaluated using the

Consistency Index - CI (Fred, 2001), obtained by

matching the clusters in the obtained partition with

the ground truth class labels. If a cluster groups two

natural classes, CI matches cluster with the class with

higher number of objects. When the clustering parti-

tions have the same number of clusters as the ground

truth, CI corresponds to the percentage of correct la-

beling, that is (1 − P

), where P

is the error prob-

ability. In this work, when extracting the ﬁnal parti-

tion, we ﬁx the number of clusters equal to the ground

truth, so the CI gives the percentage of correct label-

ing.

To obtain more information about the selection

criteria, we analyzed if the selected clusters represent

”good” or ”bad” clusters. This categorization is based

on the following: a ”good” cluster represents a group-

ing of objects belonging to only one natural cluster;

on the other hand a ”bad” cluster represents a cluster

that joins objects belonging to two (or more) different

natural clusters, that is we prefer clusters that cannot

include the overlapping between natural clusters.

0 1 2

−4

−3

−2

−1

(a) Ground truth.

0 1 2

−4

−3

−2

−1

0.60

0.88

0.90

(b) K-Means ensemble.

0 1 2

−4

−3

−2

−1

0.36

0.27

0.99

semble.

Figure 4: Examples of obtained partitions when clustering

algorithm instantiation is inadequate.

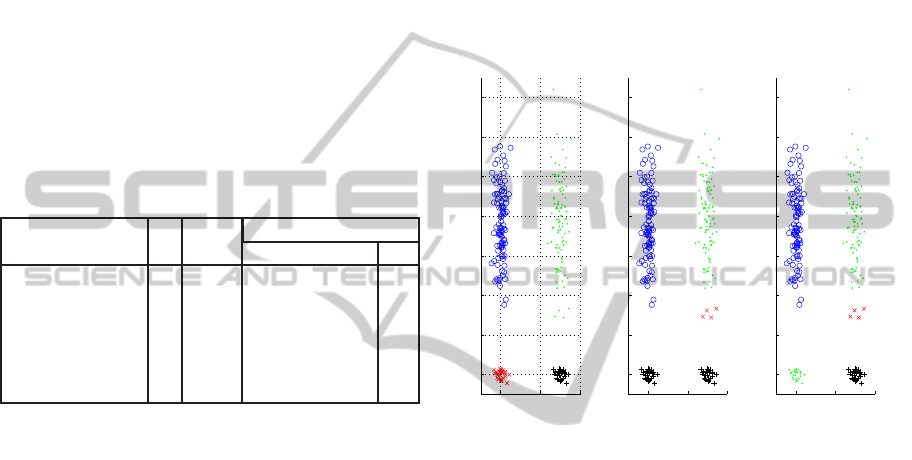
We illustrate the problem of bad clusters with

the synthetic 2D cigar data set presented in ﬁgure 4.

The data-set is composed of four distinct gaussians

(ground truth illustrated in ﬁgure 4(a)). Figures 4(b)

and 4(c) are two examples of a partitions obtained us-

ing SL as extraction method (ﬁxing the number of

clusters to K = 4) over the ensembles produced for

two different clustering algorithm instantiations: the

ﬁrst using K-Means with K = 4 and the second using

Spectral Clustering with K = 10 and σ = 0.1. The

numbers adjacent to each cluster represent the origi-

nal intrasum stability index and the letters are used

to identify each of the clusters.

In both examples we have wrong partitionings of

the data set (when compared with the ground truth

4(a)). In example 4(b) we see that the black colored

clusters (named ’D’ and marked with ’+’) have been

wrongly joined; in example 4(c) the green painted

clusters (with ’.’ marker) have also been wrongly

joined.

In the ﬁrst case the stability obtained with the in-

trasum selection index is high (0.9), but on the latter

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

496

Table 2: Selection criteria values for example of ﬁgure 4.

C ns

Match intrasum 1-intersum silh intramin 1-intermax Dunn

A 100 100 0.60 0.87 0.78 0.01 0.36 0.02

B 96 96 0.60 0.87 0.78 0.02 0.36 0.04

C 4 4 0.88 0.46 0.40 0.81 0.21 1.02

D 50 0 0.90 0.46 0.41 0.77 0.21 0.97

Table 3: Clustering results, in terms of Consistency Index, CI, using the Single Link (SL) and the Average Link hierarchical

(AL) methods. The ensembles result from combining the selected clusters from all the clustering algorithm instantiations.

Data-Sets

(SL) (AL)

intrasum intersum silh intramin intermax Dunn intrasum intersum silh intramin intermax Dunn

cigar 0.80 0.80 0.80 0.80 1.00 1.00 0.99 0.99 0.99 0.99 1.00 1.00

spiral 0.51 0.51 0.51 0.51 1.00 1.00 0.59 0.61 0.62 0.51 1.00 1.00

iris 0.67 0.67 0.67 0.67 0.34 0.34 0.90 0.90 0.90 0.67 0.34 0.34

rings 0.45 0.56 1.00 0.45 1.00 1.00 1.00 1.00 1.00 1.00 1.00 1.00

breast 0.65 0.65 0.65 0.65 0.65 0.65 0.96 0.96 0.96 0.96 0.65 0.65

image 0.68 0.68 0.68 0.33 1.00 1.00 0.98 0.98 1.00 0.33 1.00 1.00

is lower (0.279), allowing the selection of a wrong

cluster in one of the situations. Table 2 presents for

this example the values of the other proposed cluster

selection criteria. Each row represents each of the ob-

tained clusters (labelled from ’A’ to ’D’) and columns

represent: ns

-the number of samples of each cluster;

Match - the number of samples that matches the ob-

jects in the natural clusters of ﬁgure 4(a) considering

the deﬁnition of ”good” clusters; intrasum to Dunn

the selection criterion.

Considering the global selection threshold 0.9 for

intrasum

, th

intersum

, th

intramin

and th

intermin

, and 10 for

Dunn

, the cluster ’D’ (last row of the table) would

only be selected by the intrasum criteria. That is, the

other proposed cluster validity indexes are more se-

lective than the previous criterion.

To better understand the differences, consider the

co-association matrix of ﬁgure 5 which corresponds

to the example in ﬁgure 4(b). The different stability

indexes use differently the co-association values:

• The intrasum uses only the intra cluster similari-

ties. The obtained value is an average of the sim-

ilarities of the objects within the cluster in analy-

sis;

• When using the intramin instead of the average

between the similarities, the minimum similarity

is the value that is extracted (thus being more re-

strictive);

• When considering to use the inter-cluster infor-

mation, the intersum criteria averages the simi-

larities of the objects of the analysed cluster with

the ones on the closer cluster, and the intermax

uses the maximum value, being more restrictive.

In ﬁgure 5 , the color scheme ranges from blue

(C (i, j) = 0) to red (C (i, j) = 1), corresponding to

the magnitude of similarity, and the axis represent

the samples of the data-set organized such that sam-

ples belonging to the same cluster are displayed con-

tiguously. The two lower block diagonal matrices

represent the wrongly joined clusters (named ’D’).

Their intracluster similarity is very high, but when

analysing the minimum value of intracluster similar-

ity it is possible to see that this cluster is not so sta-

ble as it ﬁrst looks (0.77 similarity - compared with

an average similarity of 0.90). If we consider the in-

tercluster similarity, the corresponding stability value

will signiﬁcantly decrease. It can be noticed that there

are vertical and horizontal lines on the matrix repre-

senting higher similarity values. The inclusion of the

other sources of information avoids the inclusion of

this bad cluster (merging two ”natural” clusters) in the

ﬁnal combination process.

50 100 150 200 250

100

150

200

250

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Figure 5: K-Means ensemble (K = 4) - Example of associ-

ated co-association matrix.

SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC

497

The new proposed criteria seem more restrictive

than the intrasum (used before), selecting fewer clus-

ters from the co-association matrixes obtained from

each algorithm instantiation. Nevertheless the inte-

gration of all the algorithm instantiations, for almost

all of the benchmark data-sets, resulted in the inclu-

sion of clusters that covered all the data-set.

To summarize the results for the benchmark data-

sets, we present in table 3 the CI index using the SL

and the AL hierarchical methods as extraction meth-

ods, marking for each data-set the maximal CI value.

The right half of the table presents more marked

cells, showing that the AL extraction method con-

ducted to better results. Comparison of the results

shows that the Silhouete (silh), the intermax, and the

Dunn index systematically leads to better results than

the original intrasum selection criterium. The re-

maining do not show an evident superiority, and in-

tramin is the index presenting the worst performance.

The intermax and Dunn criteria were the best in

almost every data-set. The cases in which they did not

obtain the best results correspond to situations where

only a subset of samples was selected, since these cri-

teria selected only a small part of the evaluated clus-

ters. This fact caused that some objects were not part

of any of the selected clusters, penalizing the over-

all result, since some natural clusters didn’t have any

match.

The criterion Silhouete gave also results compa-

rable with Dunn and intermax criteria in almost all

data-sets, allowing the coverage of all objects in ev-

ery data-set.

7 CONCLUSIONS

Adopting the Multiple-Criteria Evidence Accumula-

tion Clustering method (Multi-EAC) as baseline clus-

ter combination method, we addressed the issue of

selection of meaningful clusters from the multiple

data partitions. In previous work, the authors pro-

posed a cluster validity criterion based on cluster sta-

bility, assessed from intermediate co-association ma-

trices, obtained from clustering ensembles produced

by a single clustering algorithm by perturbing the

data set using sub-sampling. In this paper we pro-

posed new cluster validity criteria for the selection of

clusters from the same intermediate co-associations

matrices but using it on a different perspective. In-

stead of considering only the intra-cluster similarity,

we propose indexes based on inter-cluster similarity

and combination of intra-cluster and inter-cluster sim-

ilarities. Comparison of the several criteria was based

on the performance of the combined data partitions,

obtained by accounting only on clusters that are se-

lected according to the corresponding criteria.

Experimental results have shown that four out of

the the ﬁve proposed criteria lead in general to better

combination results than by using the cluster stabil-

ity criterion. In particular, the criterion Silhouete and

Dunn focusing both the intra and the inter-cluster sep-

arability, and the intermax focusing on intra-cluster

separability, gave the overall best results.

Furthermore, the new methods can also be ap-

plied to clustering ensembles that do not make use of

data sub-sampling, being of more general applicabil-

ity. Additional experiments on larger data sets and on

more real data sets are underway.

REFERENCES

Asuncion, A. and Newman, D. (2007). UCI ML repository.

Ayad, H. G. and Kamel, M. S. (2008). Cumulative voting

consensus method for partitions with variable number

of clusters. IEEE Trans. Pattern Anal. Mach. Intell.,

30(1):160–173.

Ben-Hur, A., Elisseeff, A., and Guyon, I. (2002). A stabil-

ity based method for discovering structure in clustered

data. In Paciﬁc Symposium on Biocomputing.

Bezdek, J. C. and Pal, N. R. (1995). Cluster validation

with generalized dunn’s indices. In ANNES ’95: Pro-

ceedings of the 2nd New Zealand Two-Stream Interna-

tional Conference on Artiﬁcial Neural Networks and

Expert Systems, page 190, Washington, DC, USA.

IEEE Computer Society.

Bolshakova, N. and Azuaje, F. (2003). Cluster validation

techniques for genome expression data. Signal Pro-

cess., 83(4):825–833.

Dubes, R. and Jain, A. (1979). Validity studies in clustering

methodologies. Pattern Recognition, 11:235–254.

Dunn, J. C. (1974). A fuzzy relative of the isodata process

and its use in detecting compact, well separated clus-

ters. Cybernetics and Systems, 3(3):32–57.

Fern, X. Z. and Brodley, C. E. (2004). Solving cluster en-

semble problems by bipartite graph partitioning. In

ICML ’04: Proceedings of the twenty-ﬁrst interna-

tional conference on Machine learning, page 36, New

York, NY, USA. ACM.

Fred, A. (2001). Finding consistent clusters in data parti-

tions. In Kittler, J. and Roli, F., editors, Multiple Clas-

siﬁer Systems, volume 2096, pages 309–318. Springer.

Fred, A. and Jain, A. (2005). Combining multiple cluster-

ing using evidence accumulation. IEEE Trans Pattern

Analysis and Machine Intelligence, 27(6):835–850.

Fred, A. and Jain, A. (2006). Learning pairwise similarity

for data clustering. In Proc. of the 18th Int’l Confer-

ence on Pattern Recognition (ICPR), volume 1, pages

925–928, Hong Kong.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

498

Halkidi, M., Batistakis, Y., and Vazirgiannis, M. (2001). On

clustering validation techniques. Intelligent Informa-

tion Systems Journal, 17(2-3):107–145.

Halkidi, M., Batistakis, Y., and Vazirgiannis, M. (2002a).

Cluster validity methods: Part i. SIGMOD Record.

Halkidi, M., Batistakis, Y., and Vazirgiannis, M. (2002b).

Cluster validity methods: Part ii. SIGMOD Record.

Jain, A. and Dubes, R. (1988). Algorithms for Clustering

Data. Prentice Hall.

Jain, A. K. and Moreau, J. V. (1987). Bootstrap technique

in cluster analysis. Pattern Recognition, 20:547 – 568.

Lange, T., Braun, M., Roth, V., and Buhmann, J. (2002).

Stability-based model selection. In NIPS, pages 617–

624.

Levine, E. and Domany, E. (2000). Resampling method for

unsupervised estimation of cluster validity. Aaa.

Ng, A. Y., Jordan, M. I., and Weiss, Y. (2002). On spectral

clustering: Analysis and an algorithm. In T. G. Di-

etterich, S. B. and Ghahramani, Z., editors, Advances

in Neural Information Processing Systems 14, Cam-

bridge, MA.

Roth, V., Lange, T., Braun, M., and Buhmann, J. (2002). A

resampling approach to cluster validation. In Compu-

tational Statistics-COMPSTAT.

Rousseeuw, P. (1987). Silhouettes: a graphical aid to the in-

terpretation and validation of cluster analysis. Journal

of Computational and Applied Mathematics, 20:53–

65.

Sergios Theodoridis, K. K. (1999). Pattern Recogniton.

Academic Press.

Strehl, A. and Ghosh, J. (2002). Cluster ensembles - a

knowledge reuse framework for combining multiple

partitions. J. of Machine Learning Research 3.

Topchy, A., Jain, A. K., and Punch, W. (2005). Clustering

ensembles: Models of consensus and weak partitions.

IEEE Trans. Pattern Anal. Mach. Intell., 27(12):1866–

1881.

Verma, D. and Meila, M. (2003). A comparision of spec-

tral clustering algorithms. Technical report, UW CSE

Technical report.

SELECTIVELY LEARNING CLUSTERS IN MULTI-EAC

499