CrossSense

Sensemaking in a Folksonomy with Cross-modal Clustering over Content

and User Activities

Hans-Henning Gabriel, Myra Spiliopoulou

Faculty of Computer Science, Otto-von-Guericke-University Magdeburg, Magdeburg, Germany

Alexandros Nanopoulos

Institute of Informatics, Hildesheim University, Hildesheim, Germany

Keywords:

Sensemaking, Folksonomy, Social tagging, Folksonomies, Clustering, Tensor clustering.

Abstract:

Today folksonomies are of increasing importance, many different platforms emerged and millions of people

use them. We consider the case of a user who enters such a social platform and wants to get an overview of

a particular domain. The folksonomy provides abundant information for that task in the form of documents,

tags on them and users who contribute documents and tags.

We propose a process that identiﬁes a small number of thematically ”interesting objects” with respect to subject

domains. Our novel algorithm CrossSense builds clusters composed of objects of different types upon a data

tensor. It then selects pivot objects that are characteristic of one cluster and are associated with many objects

of different types from the clusters. Then, CrossSense collects all the folksonomy content that is associated

with a pivot object, i.e. the object’s world: We rank pivot objects and present the top ones to the user.

We have experimented with Bibsonomy data against a baseline that selects the most popular users, documents

and tags, accompanied by the objects most frequently co-occurring with them. Our experiments show that our

pivot objects exhibit more homogeneity and constitute a smaller set of entities to be inspected by the user.

1 INTRODUCTION

Folksonomies enjoy an increasing popularity. Plat-

forms with different functionalities have emerged and

millions of people use them. In its most basic form,

a folksonomy is a social platform where users con-

tribute resources and annotate them with tags. As

Golder and Huberman point out, tagging is ”an act of

organizing through labeling, a way of making sense of

many discrete, varied items according to their mean-

ing” (Golder and Huberman, 2006). However, how

can newcomers to a social platform make sense of the

whole platform and get a fast overview of the seman-

tics associated with it? Should they study the activi-

ties of the most active users? Perform a categorization

of the resources stored in it? Or inspect the most pop-

ular tags? In this study, we propose CrossSense that

helps a user get a better overview of a folksonomy by

identifying a limited number of representative objects

and their ”worlds”, composed of users, resources and

tags strongly associated to these representatives.

Intuitively, a site can be perceived as a set of

resources (we concentrate on documents hereafter).

Hence, a straightforward way of getting an overview

of a site’s content would be by invoking an unsuper-

vised learning method over the site’s content. For ex-

ample, one could invoke Probabilistic Latent Seman-

tic Analysis (Hofmann, 2001) to learn the hidden top-

ics in the site, or text clustering to group the docu-

ments on similarity and cluster labeling to identify the

representative words in each cluster, see e.g. (Aggar-

wal and Yu, 2006). However, such methods focus on

the content only, without considering the way users

perceive this content.

Essentially, a newcomer should be helped to per-

ceive the site in the same way as its users perceive

it. This perception is encapsulated in the users’ ac-

tivities, i.e. contributing resources and tagging them.

The interplay among users, resources and tags in a

social platform is intensively investigated, mostly in

the context of recommendation engines. Marco de

Gemmis et al. consider tags next to content to infer

100

Gabriel H., Spiliopoulou M. and Nanopoulos A..

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities.

DOI: 10.5220/0003101101000111

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 100-111

ISBN: 978-989-8425-28-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

user interests and thus enhance the content-based rec-

ommender of a folksonomy site (de Gemmis et al.,

2008). Begelman et al. capture tags, users and an-

notated resources on a tensor (Begeman et al., 2006).

Tensor-based clustering for recommendations has in-

deed gained momentum in the last years; Symeonidis

et al. show that considering all relationships involving

users, tags and resources leads to superior recommen-

dation performance (Symeonidis et al., 2010). How-

ever, the objective of such studies is to ﬁnd the most

relevant objects to a user rather than describe a whole

site with a limited number of representatives.

Our method CrossSense models the different types

of objects (users, documents, tags) of a social plat-

form as a tensor. We use tensor decomposition and

clustering to organize the platform’s objects in groups

that reﬂect the associations among them. We consider

different perspectives, i.e. different combinations of

tensor modes, for clustering, and choose the represen-

tatives of the site, which we term pivot objects, among

the objects that are present in clusters of multiple per-

spectives. Keeping in mind that little may be known

for a pivot object beyond its name (that is uninforma-

tive for users and for many tags), we build for each

pivot object its world, comprised of the objects most

likely to co-occur with it. Then, the overview of a so-

cial platform is mapped to the inspection of a small

set of pivot objects and their worlds, whereupon we

rank these objects on two properties: interestingness

and world stability.

We illustrate the main idea of CrossSense in Fig-

ure 1. The objects in the ﬁgure (circles, triangles and

stars) correspond to different types of objects in a so-

cial platform’s site, i.e.documents (as circles), users

(as stars) and tags (as triangles), and thus to the cor-

responding modes of the tensor. A perspective en-

compasses objects of at least two different modi; Per-

spectives 2 and 3 in the Figure cover objects of two

modes (documents and users, resp. documents and

tags), Perspective 3 of three modes. Within each per-

spective, we see the objects grouped in three clusters.

To provide an overview of the social platform, one

could deliver these 9 clusters or their representative

objects. However, the three perspectives are different

views over the same data, i.e. they partially overlap.

A pivot object is a representative of multiple clus-

ters that belong to different perspectives but overlap

in content. In Figure 1, the object marked with a p

is a pivot object that stands for three clusters, one in

each perspective.

The pivot p in Figure 1 belongs to the mode

of documents (circles). Hence to describe ”its” clus-

ter in Perspective 1 we also need user objects (stars),

and similarly for the other two perspectives. The

Figure 1: Three perspectives over a site, Pivot object and

associated objects from different perspectives.

objects associated frequently with the pivot consti-

tute its world, comprised of the green-shaded objects

in Figure 1: the green-shaded user/star and docu-

ments/circles in Perspective 1 also appear together

with the pivot in Perspective 3, indicating that part of

the pivot’s world persists from one perspective to the

other. Instead of delivering three clusters as part of

the site’s description, CrossSense would deliver their

pivot object and the 4 distinct objects constituting its

world across the three perspectives.

The paper is organized as follows. In the next

section we start with the problem deﬁnition, then

introduce pivot objects and their worlds and deﬁne

the properties that make a pivot object interesting,

namely interestingness and stability. We then present

CrossSense, i.e. the steps of tensor-based modeling

of the folksonomy, clustering upon the tensor, extrac-

tion and ranking of pivot candidates and their worlds,

and ﬁltering of uninteresting candidates. In section 4

we introduce a baseline method and evaluate our ap-

proach against it. Related work is presented in section

5. The last section concludes our study.

2 FINDING THE PIVOT OBJECTS

OF A SOCIAL PLATFORM

Objective of our investigation is to assist a newcomer

to a social platform by delivering a small number of

objects for inspection: these objects must be so cho-

sen as to provide an insight on the topics of impor-

tance in this platform. Which objects to choose and

of which type? A social platform is populated by

users who contribute resources (we concentrate on

documents) and tags. In terms of content, it might

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

101

look reasonable to supply the newcomer with infor-

mation about the documents in the collection, but this

overlooks the social aspects of the platform, includ-

ing the role of users in it and the way they perceive

documents by tagging them. On the other hand, the

only information typically available for a user is some

identiﬁer, while some tags have at least an informative

name but others have not (contrast a tag ”good” with

a tag ”machine learning”).

Hence, our objective translates into ﬁnding a dis-

ciplined selection of objects from the platform, allow-

ing for all types of objects but providing some way

of ranking among individual objects. Our method

CrossSense starts with modeling documents, users

and tags in a tensor, so as to highlight the relation-

ships among them. We perform tensor decomposition

and clustering on these data and derive cross-modal

clusters that contain objects of two or all three types

(all types in the general case). We introduce a mea-

sure of interestingness to rank cluster members and

select the top-k ones as candidate pivot objects, i.e. as

representatives of the platform’s content. For each of

these top-k candidates we identify closely associated

objects; they constitute the candidate’s world. We

then select as pivot objects those that have the highest

interestingness and the most stable worlds.

We ﬁrst present our tensor model, specify per-

spectives over the data and explain how cross-modal

clustering is done on them. We then introduce pivot

objects and their worlds and deﬁne interestingness

and stability on them. Finally, we describe the

CrossSense algorithm that extracts, ranks and selects

the pivot objects to be presented to the user. Our no-

tation is captured in Table 1 and explained in sequel.

Table 1: All variables used in this work.

Notation Description

M Set of all modi

X ∈ R

×...×N

|M|

Tensor with |M| modi

P Subset of modi that constitute

a perspective

Cross-modal clustering with

modi from P

x Candidate object

Subset of clusters in which x

appears

C Set of all clusterings

τ Threshold for minimum

number of co-occurences

World of x w.r.t. threshold τ

2.1 Perspectives over Multi-modal Data

To identify pivot objects, i.e. objects that are rep-

resentative of the subdomains in the folksonomy,

we must ﬁrst form the subdomains as object clus-

ters, exploiting the relationships among them, namely

that a user contributes resources, a user contributes

tags, a tag annotates resources. These types of ob-

jects constitute the set of modi M of a tensor X ∈

×...×N

|M|

, where N

is the cardinality of the i

mode. For a typical folksonomy we consider M =

{users,tags,resources}; a digital library may have

modi like articles, conferences, authors, editors etc.

Deﬁnition 1. Given is a tensor X ∈ R

×...×N

|M|

and

M the set of modi in this tensor. A ”perspective” P

is a combination of at least two distinct modi, i.e. an

element of Powerset P(M) \{m ∈ M ∪

0}.

We use perspectives instead of single modi since

we would like to discover objects of different types

that thematically belong together and describe the

pivot objects. As pivot objects we consider only ob-

jects that appear in clusters of at least one perspective.

This means that an object is a candidate pivot only if

it is strongly associated with other objects, whereby

the notion of ”strong association” will be captured

through the eigenvalues of the eigenvectors of the core

tensor, as we will see below.

For tensor-based clustering we use the method

proposed in (Sun et al., 2006): Singular Value De-

composition (SVD) is performed upon the original

feature space and a core tensor is derived with Tucker

decomposition. Similar to Sun et al., we build a clus-

ter by considering only the positions with the top-n

eigenvalues (absolute values, for some parameter n).

A high value in the core tensor implies that the objects

in the corresponding eigenvector are strongly associ-

ated. The value in the core tensor points to a particu-

lar eigenvector from each mode. By our deﬁnition of

perspective, we perform clustering only upon combi-

nations of at least two modi; such a cluster contains

objects of different types, so we term it a cross-modal

cluster. A pivot candidate is then an object from

eigenvectors a high value in the core tensor points to,

and that have high energy in the eigenvectors. High

energy means that the SVD has associated the object

with a high absolute value in the eigenvector. But

pivot objects must satisfy further constraints, as we

explain in the next subsection.

2.2 Pivot Objects and their

Interestingness

A pivot object is a representative of a cross-modal

cluster. It must have following properties:

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

102

• It contributes to at least one cluster in many per-

spectives,

• is associated with the same objects in several per-

spectives and

• does not contribute to many clusters of the same

perspective.

The ﬁrst property states that a pivot object must be

characteristic of some cluster; in tensor-based cluster-

ing we, quite naturally, use energy as criterion. The

third property excludes objects that are characteris-

tic of many clusters within the same perspective, be-

cause they are not informative. For example, consider

a tag associated with many objects: the two proper-

ties together say that if these objects form one coher-

ent group, then the tag is a pivot candidate, but if they

form many groups it is not. The second property says

that a pivot object must cover multiple perspectives,

but it must be associated with the same objects. For

example, consider a tag associated with documents

on machine learning in the ”tag-resource” perspective

(two object types) and take the ”tag-resource-user”

perspective (three object types): if the tag contributes

to a cluster on machine learning documents, then it is

a good pivot object that associates the hidden subject

”machine learning” with both documents and users.

If the tag rather contributes to a cluster with machine

learning documents in the ﬁrst (two-modi) perspec-

tive and to a cluster with image processing documents

in the second (three-modi) perspective, then it is a less

good candidate.

Since in the ﬁrst place all objects from the origi-

nal data set are candidates to be pivot objects, we need

some criteria on which we base the decision whether a

candidate becomes a pivot object or not. The ﬁrst cri-

terion to be fulﬁlled is that we require a candidate to

be under the top-m interesting objects. We motivate

interestingness of a candidate as follows: Though a

candidate object may be representative of a domain

that describes part of the folksonomy and this domain

can be viewed from different perspectives, still within

a single perspective the candidate object may occur in

different clusters (and thus causes the clusters to over-

lap) which is not desired w.r.t. the third property for

pivot objects. This results in two antagonistic ways

a candidate object inﬂuences its interestingness: the

more often it occurs in the same perspective but in

different clusters the less informative it is; the more

often it occurs in different perspectives, the more in-

formative it is. Thus, we deﬁne interestingness as fol-

lows:

Deﬁnition 2. Let C =

P∈P(M)\{m∈M∪

{ξ

} be the

set of all clusterings, where ξ

is the clustering for

perspective i. Let x be a pivot candidate. We deﬁne

the interestingness of x over all perspectives in C as

the number of clusterings where x appears , divided

by the maximum number of times x appears within a

single clustering.

In particular, let B

x,i

= {A ∈ ξ

|x ∈ A} be the sub-

set of clusters in ξ

for perspective i, in which x ap-

pears. Then:

interestingness(x,C) =

| ∪

i=1...|P|,B

x,i

max

|P|

i=1

x,i

(1)

The range of the interestingness function is

[0,+∞], higher values are better. Candidates with an

interestingness of less than 1, i.e. objects that ap-

pear in only one perspective, are pruned right away

(see Algorithm CrossSense in subsection 3). The de-

sirable properties of a pivot candidate, i.e. appear-

ing in many perspectives and appearing in only few

(preferably only one) cluster in each perspective, are

reﬂected in the nominator, resp. denominator of the

interestingness function.

2.3 The World of a Pivot Object

The second criterion to be fulﬁlled is that we require a

candidate to be associated with one of the top-q stable

worlds. Thus, before we motivate stability, we have

to deﬁne what the world of a candidate object is. We

say that the world of a candidate object are all objects

frequently co-occurring with it:

Deﬁnition 3. Let x be a pivot candidate, let C be the

set of all clusterings over the perspectives of tensor X

as in Def. 2. For each perspective i, let ξ

∈ C be the

corresponding clustering and let B

x,i

= {A ∈ ξ

|x ∈

A} ⊆ ξ

be the set of clusters in ξ

which contain x.

The ”world” of x under threshold τ, W

, is the set

of objects co-occurring with x at least τ times in the

clustering of some perspective i.

In particular, let y 6= x be an object such as there is

an A ∈ B

with y ∈ A. The number of co-occurrences

of y with x is cooccur

(y) =

∑

i=1



∑

A∈B

x,i

|A ∩ {y}|



i.e. the number of clusters over all perspectives where

both x and y appear. Then the world of x under τ is

deﬁned as:

= {y|cooccur

(y) ≥ τ} (2)

In the trivial case of τ = 1, the world of a pivot

candidate x would consist of all objects that ever ap-

peared together with x in a cluster of some perspec-

tive. By increasing τ, objects with few co-occurrences

with x can be excluded. However, the fact that x ap-

pears in different perspectives should also be consid-

ered. For example, assume that x is a document that

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

103

co-occurs with some tags t,t

,.. . and some docu-

ments d,d

,.. . under the perspective i of documents

and tags. When we consider the perspective j of doc-

uments and users, it is intuitive to expect that some

of d, d

,.. . also appear in the same cluster as x in that

perspective. If this is the case, then the association

of x with these documents is more stable than if x

were associated with completely different documents.

From this consideration we derive the notion of world

stability: the world of pivot candidate x is the more

stable, the more often its elements co-occur with x.

Deﬁnition 4. Let x be a pivot candidate and let W

be its world under threshold τ. The stability of this

world is deﬁned as:

stability(W

) =

∑

y∈W

cooccur

(y)

τ × |W

(3)

The range of world stability is [1,+∞), where

higher values are better. The lowermost value cor-

responds to the case where each element of the world

appears no more than τ times (i.e. the lower bound-

ary) together with x.

We use the concepts of interestingness and world

stability to select a set of pivot candidates and their

corresponding worlds. In particular, we can choose all

pivot candidates whose worlds are not empty, given

τ. However, we can constraint the output further

by ranking the pivot candidates on interestingness,

choose the top-m ones for some m, compute their

worlds, rank them on stability and choose the top-

q ones. Hence, the output to the newcomer is a

set of the q most interesting pivot objects and their

worlds. In the next subsection we show the algo-

rithm CrossSense that computes this set of pivot ob-

jects given threshold values τ,m,q.

3 ALGORITHM CrossSense

Our algorithm CrossSense takes as input a tensor X

with a set of M modes and derives m pivot candidates,

ranked on interestingness, and at most q ≤ m worlds,

ranked on stability. It outputs the best pivot objects

with respect to interestingness and stability of their

worlds; if q = m, then m pivot objects are returned,

otherwise only the top-q ones are output.

CrossSense builds cross-modal clusters using ten-

sor analysis techniques, and thus requires the num-

ber of clusters y per perspective as input. From each

cross-modal cluster we select n initial pivot candi-

dates per mode, i.e. n × |M| candidates. Of these,

the top-m candidates will be chosen in the algorithm’s

second loop, as explained below.

Algorithm 1. CrossSense.

1: Input:

2: Tensor X ∈ R

×···×N

|M|

3: y: number of clusters to be build

4: n: number of objects from each eigenvector

5: τ: frequency threshold for object co-occurrence

within the world of a pivot candidate

6: m: top-m interesting pivot candidates

7: q: top-q stable worlds (q ≤ m)

8: Output:

9: Set T = ∪

i=1

{(W

)} of pivot objects and their

worlds

10: Algorithm:

11: C ←

0; // init set of all clusterings

12: for all P in P(M) \ {m ∈ M ∪

0} do

13: derive X

from X with modes in P

14: derive clustering ξ

of y clusters from X

, each

including n objects per object type

15: C ← C

;

16: end for

17: T ←

0; // init set of all pairs (W

,x)

18: X ←

0; // init set of quadruples for all candidates

19: for all ξ

in C do

20: for all x in ξ

21: if |B

x,P

| < y/2 then update(X, x, B

x,P

)

22: end for

23: end for

24: compute interestingness and stability for all

quadruples in X

25: if x ∈ X among top-m and W

among top-q then

T ← T

,x)

Table 2: Left: Three-mode tensor with eight entries. Right:

Tensor reduced to two-modi.

1,2,1 : 1 1,2 : 3

1,2,3 : 1 3,3 : 2

1,2,7 : 1 4,5 : 1

3,3,1 : 1 7,1 : 2

3,3,8 : 1

4,5,2 : 1

7,1,7 : 1

7,1,9 : 1

The ﬁrst loop of CrossSense derives a clustering for

each perspective P (lines 12-16). First step in the ﬁrst

loop is to reduce the modality of original tensor X

from |M| to |P| (line 13). This is done iteratively -

one mode less at a time. Reducing modality is done

by ﬁxing the modes that are to be remained and sum-

ming up the values in the tensor from the mode that is

to be reduced. Consider for example the sparse rep-

resentation of a tensor in left column of Table 2. This

is a three-mode tensor having eight entries equal to

one, comma separated are the indices (one per mode)

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

104

pointing to the entries. In the right column the three-

mode tensor is reduced to a two-mode tensor by ﬁxing

mode one and two and summing up the values for all

occurrences in mode three.

In a next step (line 14) from the reduced tensor

we derive the clustering ξ

using a generalization

of PCA: We derive a number of eigenvectors for each

mode and we derive the core tensor (Sun et al., 2006).

Entries in the core tensor point to eigenvectors that are

to be combined. From the combined eigenvectors we

choose those objects with highest energy (highest ab-

solute value) that form our cross modal clusters. Pa-

rameters in this generalized PCA are y for the number

of cross modal clusters to be build (y values of high-

est energy from core tensor) and n for the number of

objects to choose from each eigenvector (again values

of highest energy). All clusterings derived this way

are collected into set C (line 15).

Although we have as many perspectives as are the

combinations of at least two modes, we must keep in

mind that (a) the number of modes in a social plat-

form is not large, and (b) the number of object types

that should be delivered to a newcomer for inspection

should be kept low anyway, to avoid confusion.

The second loop of CrossSense computes the pivot

objects and their worlds by iteratively updating a set

of quadruples, where each quadruple contains infor-

mation required to decide whether a candidate object

will become a pivot object. These information are the

object itself (x), the number of clusterings where x ap-

pears (|∪

i=1...P,B

x,i

|) (cf. Deﬁnition 2), the maxi-

mum number of times x appears within the same clus-

tering (max

i=1

x,i

|) and the world W

of x. Note that

we store the world of x as a set of pairs (co-occurring

object, number of co-occurrences), which is all infor-

mation needed to compute stability of the world.

Initially, for each perspective P, all n × |P| objects

in ξ

are candidates (line 20). But only if x belongs

to less than y/2 clusters in ξ

, it is considered for fur-

ther investigation, otherwise x is pruned away (line

21): although it is desirable that x appears in several

perspectives, it is not desirable that it appears in many

clusters of the same perspective, as this indicates am-

biguous semantics (e.g. a tag that appears in both

a cluster with documents on machine learning and a

cluster with documents on robotics). If x fulﬁlls this

condition it is passed to the update function (line 21),

which is shown in Algorithm 2.

Input to the update function is the set X of all

quadruples, the current candidate object o and all

clusters B from current clustering ξ

, where o ap-

pears. In a ﬁrst step we extract from B all objects

that are co-occurring with o and store them as pairs

together with their frequency (number of clusters in B

Algorithm 2. Update.

1: Input:

2: X: Set of all quadruples (x: candidate, a: num-

ber of clusterings where x appears, b: maximum

number of times x appears within single cluster-

ing, W

: world of x )

3: o: Candidate object

4: B: All clusters containing o

5: Algorithm:

6: extract W

from B as set of pairs (co-occurring

object, number of co-occurrences);

7: if X does not contain quadruple with o then

8: X ← X

(o,1,|B|,W

);

9: else

10: t is quadruple from X, where t

= o;

11: update t

= t

+ 1;

12: update t

= max (t

,|B|);

13: update t

= t

∪W

; // sum up co-occurrences

where such an object co-occurs with o) in W

(line 6).

If there is not yet a quadruple for candidate object o,

we create one and add it to the set of all quadruples

X (line 8). Otherwise the existing quadruple in X is

updated: the number of clusterings where o appears

is incremented (line 11) and the maximum number of

appearances within a single clustering is updated by

simply taking the maximum as in line 12. And the

world is updated by summing up the frequencies of

objects that are already in the world and in B, and

adding those objects (and frequencies) from B to the

world that have not yet been in it.

In Algorithm 1 we can then compute interesting-

ness and stability for each quadruple in X (line 24)

since all information needed is stored in a quadru-

ple (cf. Deﬁnition 2 and Deﬁnition 4). Finally in

Algorithm 1 we decide whether a candidate and its

world from X will become a pivot object or not. To do

so, we ﬁrst rank the candidates by interestingness and

choose the top-m from them. We then check whether

its world is one of the top-q worlds ranked by stabil-

ity. Finally, we can return T that contains the pivot

objects and their worlds.

4 EVALUATION

Objective of the evaluation is to check whether

our mechanism delivers more intuitive semantics for

sensemaking than a baseline that returns the top-k

tags, documents and users associated with a given

pivot object.

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

105

4.1 Dataset

To see how our method helps a user in sensemaking

in a folksonomy we use the Bibsonomy dataset. The

data is from the year 2007 and originally comprises

335.789 transactions. A transaction is of the form

(userId, tagId, documentId). This means that the user

with the userId has the tagged the document with the

given documentId with the tag of the given tagId. We

prepared this dataset with a number of steps listed be-

low:

• We removed all transactions with documents that

occur in less than four transactions.

• We removed all transactions with tags that occur

in less than four transactions.

• We removed all transactions with tags that occur

more than 100 times.

The basic idea behind these preparation steps is to re-

move the long tail and to remove very frequent items

that do not contain useful information. After these

preparation steps, from 335.789 transactions 41.729

have remained. Furthermore we split up the data into

four subsets - one subset per quarter of the year. Table

Table 3: Number of transactions and distinct objects for

each quarter of the year 2007.

Quarter Number of Users Tags Docs

Transactions

1 4.696 69 1226 643

2 15.833 81 2330 2024

3 15.143 83 2132 1783

4 6.057 97 1432 791

3 shows for each quarter how many transactions it

contains. Also this table shows how many distinct

objects of each object type there are in each quarter.

4.2 Setup

4.2.1 Homogeneity

To be able to compare quality of Clusters we intro-

duce special homogeneity measures for the Bibson-

omy dataset. To measure homogeneity of a cross-

modal cluster Y

| P = {user,tag,document}, we uti-

lize co-occurence counts from objects of different

type in that cluster. We count the number d

of doc-

uments in Y

that were annotated by the users in that

cluster. We count the number d

of documents in Y

that were annotated with tags from that cluster. Ho-

mogeneity w.r.t. documents is then measured as

+ d

2 ∗ numDocs

(4)

where numDocs is the number of documents in the

cluster. Similarily we deﬁne homogeneity w.r.t. the

other two object types tag and user:

2 ∗ numTags

(5)

+ u

2 ∗ numDocs

(6)

In the above equations, t

is the number of tags in

that were used by any of the users in that cluster,

is the number of tags that were used with any of

the documents in that cluster. Respectively, u

is the

number of users that have annotated any of the docu-

ments in the cluster and u

is the number of users that

have used any of the tags in the cluster.

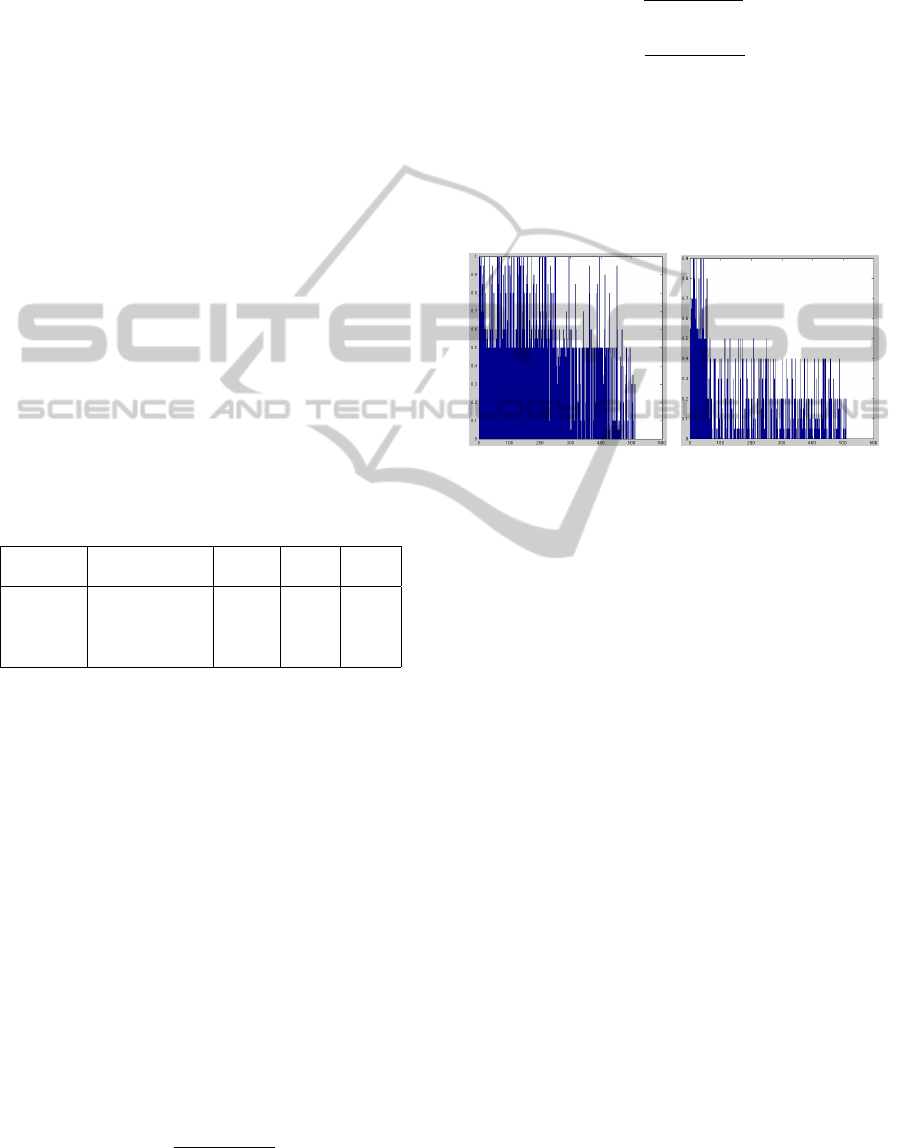
(a) (b)

Figure 2: Homogeneity (left) and corresponding baselines

(right).

4.2.2 Baseline

In order to get a baseline for a particular cluster we

use an approach of two steps:

• First, for each object type in Y

we choose a ran-

dom object from the cluster.

• Then we try to ﬁnd the top-n most similar objects

of the same type from the database, for each ob-

ject type.

This gives us a baseline cluster with top-n times |P|

objects. As similarity measure in the second step, we

use a straight forward approach by adapting a tech-

nique proposed in (Markines et al., 2009a): We ﬂatten

the 3-mode data to 2-dimensional space and measure

similarity as the euclidian distance between objects

in that space. For the process of ﬂattening, we use

the same procedure as in algorithm 1. For example,

to ﬁnd the most similar tags to a given tag, we ﬁrst

create a 2-dimensional matrix where rows are docu-

ments, columns are tags and where an entry is the fre-

quency the document was annotated with the tag by

any user. This gives a frequency vector for each tag

and distances between these vectors can be computed

by applying standard measures like cosine similarity.

Analogous we do this to ﬁnd most similar users and

documents for a given user or document.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

106

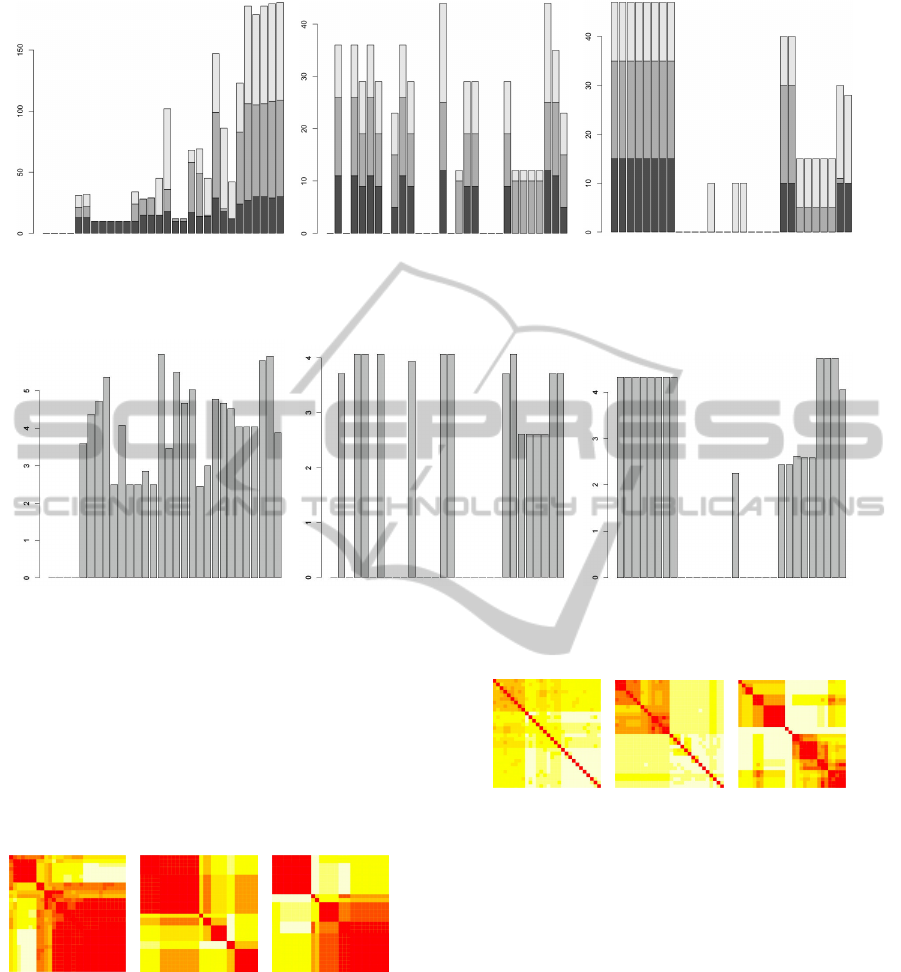
(a) (b) (c)

Figure 3: Homogeneity h

(left), h

(middle) and h

(right) for ﬁrst 20 clusters derived from core-tensor, compared to base-

lines. Left bar: derived cluster; Right bar: baseline.

Table 4: First three cross-modal clusters derived from dataset of ﬁrst two quarters.

Cluster Tags Documents

1 semantics, taggingsemantic, Trend Detection in Folksonomies. Emergent Semantics in BibSonomy.

semantictagging, tagging, FolkRank: A Ranking Algorithm for Folksonomies. TRIAS - An Algorithm for

library Mining Iceberg Tri-Lattices. Proceedings of the First Workshop on Semantic

Network Analysis.

2 poetry, poebeat, poems, Dream Haibun. Implacable Time and the Long, Slow Pull of the Irresistible

poets, poetics Sun. Across the Table. Going on About Haibun. Divorce Ceremony.

3 magnetic, resonance, Diffusion tensor imaging in multiple sclerosis: a tool for monitoring changes

brain, humans, image in normal-appearing white matter. Applications of diffusion tensor MR imaging

in multiple sclerosis. Diffusion tensor imaging of cerebral white matter: a

pictorial review of physics, ﬁber tract anatomy, and tumor imaging patterns.

Diffusion tensor imaging of early relapsing-remitting multiple sclerosis with

histogram analysis using automated segmentation and brain volume correction.

The pathogenesis of lesions and normal-appearing white matter changes in

multiple sclerosis: a serial diffusion MRI study.

4.3 Results

In a ﬁrst experiment we investigate how homogene-

ity of cross-modal clusters develops, compared to the

baseline, when clusters are sorted by energy values

provided by the core-tensor. As described in Section

2.1, the core tensor can be used to decide which eigen-

vectors to choose to form a cross-modal cluster. The

greater an entry in the core-tensor, the greater the cor-

relation between corresponding eigenvectors. We uti-

lize this property to show how homogeneity of these

clusters develops w.r.t. correlation-strength between

the different eigenvectors. To do so, we ﬁrst order the

entries of the core-tensor by size (descending) and we

then create all the corresponding cross-modal clus-

ters. We measure homogeneity h

of these clusters

and their corresponding baselines as described above.

As dataset we use ﬁrst two quarters from all transac-

tions. Results are shown in Figure 2.

A ﬁrst observation is that as correlation decreases,

the homogeneity decreases as well (in both plots).

Also it can be seen that clusters from the baseline

are often of less homogeneity than their correspond-

ing clusters from our method.

To see things in greater detail, in Figure 3 we show

only the ﬁrst 20 clusters, directly compared to their

baselines for all three homogeneity measures.

For each cluster there are two bars: left bar is ho-

mogeneity of the cluster, right bar is homogeneity of

its baseline. In all three plots, the great majority of

clusters derived by our method is of equal or greater

homogeneity than the baseline. Only in few cases (six

for h

, ﬁve for h

and six for h

) the homogeneity of

baseline clusters is greater. Also an interesting obser-

vation is that homogeneity measures based on docu-

ments (h

) is on average greater than the values mea-

sured based on tags (h

) which on average are greater

than the values measured based on users (h

). The

worse result for h

may stem from the fact that there

are only few distinct users in the dataset (cf. Table 3),

but much more distinct tags and documents.

To give a better impression what the actual clus-

ters look like, in Table 4 we show the contents of ﬁrst

three cross modal clusters, derived from data of ﬁrst

two quarters. We show the top-5 objects of each type,

for documents we show the title of the document. For

anonymization reasons we do not show the names of

the users in the clusters. The table shows that the

top three cross modal clusters are of the different top-

ics semantic tagging, poetry and magnetic resonance

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

107

(a)

(b)

Figure 4: Interestingness for all unique objects from all per-

spectives. Top: based on data from q1; Bottom: data from

q1 and q2.

imaging. It can also be seen that within one cluster

documents and tags are from the same topic.

In a second experiment we investigate how inter-

estingness is distributed among all users, tags and

documents. Therefor we ﬁrst derive all unique ob-

jects of a certain type (e.g. all unique users) from all

clusterings across all perspectives. Then we compute

interestingness values for each of these objects and

plot them in descending order. We show the result in

Figure 4.

One observation is that different object types have

completely different levels of interestingness. For ex-

ample in the ﬁrst plot, interestingness of top users is

always less than interestingness of top tags or top doc-

uments. Also we can see that the number of distinct

objects strongly varies between different object types.

There are much less distinct users than distinct tags or

documents. On the other hand, the results do not dif-

fer very much if we use twice as much data (two quar-

ters in plot b). Also it can be seen that interestingness

decreases fast, there are relatively few objects of each

type, that have very high interestingness values.

For the next experiment we apply a slightly ad-

justed version of our algorithm. We do not derive

top-m pivot objects and their worlds from all objects

across all object types. Rather we investigate each ob-

ject type and derive top-m=30 objects from each type

together with the worlds. We do so to get better in-

sight how results are inﬂuenced by choice of object

type, when objects are sorted decreasing on interest-

ingness. Thus, we derive the top-m users, top-m tags

and top-m documents (m=30), ordered on interesting-

ness, and derive their worlds. We show the size of

these worlds in Figure 5. Each bar shows the size of

the world of the corresponding object. The bars are

of up to three parts: bright is the fraction of users,

grey is the fraction of tags and dark is the fraction

of documents. From the ﬁgure we see that depend-

ing on object type the size of worlds can vary heavily.

Note that a world can be empty, which is the case if

the number of co-occurrences of an object with the

candidate object is always less than τ. For top user

worlds the size increases with decreasing interesting-

ness. Another observation is that the fraction of doc-

uments is decreasing. The sizes of top tag worlds

are independent from interestingness values. In docu-

ment worlds, with decreasing interestingness, the size

of the world decreases as well.

In Figure 6 we show for each of the worlds corre-

sponding stability values. For the case that a world is

empty, its stability is equal to zero. We can observe

that stability of worlds is independent from size of the

worlds. There can be small worlds that are more sta-

ble that big worlds and vice versa. Also stability is not

inﬂuenced by interestingness. There can be worlds of

less interesting candidate objects that are still stable.

In a ﬁnal experiment we measure diversity be-

tween the worlds we derived with CrossSense and

compare it with diversity of worlds derived as a base-

line, based on co-occurrences of original data objects.

For the newcomer who wants to get an overview of

the folksonomy it is desired that the worlds presented

to her are diverse from each other. Otherwise there

would not be much information from the objects and

their relation in the folksonomy. In particular the

baseline worlds are derived in two steps: First we de-

rive top-m most frequent objects of each type, which

are the candidate objects. Baseline worlds are then

composed of top-n=10 most frequently co-occurring

objects from the other two types and top-n most sim-

ilar objects of the same type as the candidate object

(Similarity is computed the same way as for the base-

line in Section 4.2.2.). Diversity between two worlds

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

108

(a) (b) (c)

Figure 5: Size of worlds for top-m=30 candidate objects, for each object type. Left: worlds for user-candidate objects; Middle:

for tags; Right: for documents.

(a) (b) (c)

Figure 6: Corresponding stabilities for all worlds.

is then computed by subtracting the intersection from

the union of the two worlds and taking the cardinal-

ity from this set, which is equal to the number of ob-

jects that occur in one world but not in the other. Di-

versities between worlds derived with CrossSense are

shown in Figure 7. Diversity between baseline worlds

is shown in Figure 8.

(a) (b) (c)

Figure 7: Diversity between top worlds derived with

CrossSense. Left: user worlds, Middle: tag worlds, Right:

document worlds.

The worlds used in Figure 7 are the same as the

worlds in Figure 5 and Figure 6. The left heatmap

shows diversity of each user world compared with all

other user worlds. When diversity of a world com-

pared with itself is computed, the value is equal to

zero, since union-intersection is the empty set in this

case. Thus, on diagonal color is dark which means

(a) (b) (c)

Figure 8: Diversity between corresponding top baseline

worlds.

that value of diversity is low (bright color means that

diversity between the two worlds is high). In the

left heatmap we can observe that there are two main

blocks of dark color. This can be interpreted as there

are two main types of user worlds that are really di-

verse from each other. From tag worlds we can ﬁnd

at most six worlds that differ much from each other.

From document worlds there are two big groups of

worlds and two single worlds that differ a lot from

each other. The left heatmap of Figure 8 gives the

impression that all worlds are very diverse from each

other since color is bright everywhere (except on di-

agonal). But when looking at the actual values of

diversity (also baseline user and tag worlds) it be-

comes clear that all the worlds are actually very sim-

ilar to each other (differing only slightly) and on di-

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

109

agonal they are identical (differing not at all). Still

the heatmap distributes the values on the entire range

from dark to bright. Note that this is not the case for

heatmaps in Figure 7! To summarize observations of

diversity - our method ﬁnds groups of worlds that are

diverse from each other while the baseline worlds are

very similar to each other. Also diversity of worlds

is dependent of object type that is chosen for the can-

didate object. For example our method derives two

diverse groups of user worlds but six diverse groups

of tag worlds.

5 RELATED WORK

Objective of CrossSense is to provide a user with an

overview of a folksonomy, not just a summary of its

contents. This corresponds to sensemaking, as the

term is used by Golder and Huberman (Golder and

Huberman, 2006), except that we do not refer to the

set of resources tagged by a user but to all resources,

as tagged by all users. This implies capturing and ex-

ploiting the relationship among users, resources (doc-

uments) and tags, as is typically done in tensor-based

analysis of social platforms (see e.g. (Symeonidis

et al., 2010).

Tensors are attracting increasing usage in data

mining applications, especially for clustering com-

plex data. (Banerjee et al., 2007) propose a principled

multi-way clustering framework for relational data,

wherein different types of entities are simultaneously

clustered based not only on their intrinsic attribute

values, but also on the multiple relations between the

entities. Abdu and Salane present a novel spectral-

based algorithm for clustering categorical data that

combines attribute relationship and dimension reduc-

tion techniques found in Principal Component Anal-

ysis and Latent Semantic Indexing (Abdu and Salane,

2009). The web clustering method of (Zhou et al.,

2009) aggregates web objects into various categories

according to underlying relationships among them;

it uses tensor decomposition to co-cluster web ob-

jects based on the analysis of user navigational tasks.

These methods successfully derive groups of asso-

ciated objects from a tensor, but do not address the

problem of presenting a small, yet representative sub-

set of these objects to the user.

Content summarization has been investigated in

the context of deriving a summary from one or

more documents and in the context of providing an

overview of an archive’s content. The second context

is relevant here and includes methods that study sum-

maries of text databases, like (Ipeirotis et al., 2005),

text clustering and cluster labeling, like (Aggarwal

and Yu, 2006), and topic modeling like Probabilis-

tic Latent Semantic Indexing (Hofmann, 2001). Such

methods can be transferred into tensor-based clus-

tering. For example, the aforementioned method of

Abdu and Salane uses data summaries that consist

of attribute occurrence and co-occurrence frequencies

to create a set of vectors, called ”candidate cluster

representatives”, each of which represents a cluster

(Abdu and Salane, 2009). Although such represen-

tatives are human-readable, they are not intended to

serve as a description of a social platform, and they

can be argued to be less intuitive than a list of repre-

sentative documents, users and tags, as delivered by

CrossSense.

The importance of comprehensible cluster labels

is stressed in (Osinski, 2006), where different matrix

factorizations are used to organize document sum-

maries into human-interpretable thematic categories.

Albeit summarization refers to summaries of single

documents (ﬁrst type of context summarization men-

tioned above), the main emphasis is on what the au-

thor calls ”description-comes-ﬁrst clustering” of these

summaries. The method is conﬁned to text clusters

though and has not been designed to deal with other

types of features.

Remotely related to our work are studies on as-

sessing the semantics of tags: Heymann and Garcia-

Molina use a hierarchical clustering algorithm to

build a semantic hierarchy of tags; the algorithm

operates upon a tag similarity graph, and takes tag

centrality of this graph and co-occurrence of tags

on documents into account (Heymann and Garcia-

Molina, 2006). The concept of semantic grounding

is discussed in (Cattuto et al., 2008; Markines et al.,

2009b): it refers to ﬁnding the meaning of a tag by

consulting WordNet or similar resources. Such works

are orthogonal to ours, since their aim is to extract

and present the semantics of the tags in the platform,

rather than an overview of the platform itself.

6 CONCLUSIONS

We addressed the problem of sensemaking in a folk-

sonomy. We wanted to present the user a minimal set

of objects that describe the folksonomy from different

perspectives and helps the user to get an overview of a

particular domain she is interested in. We developed

our new algorithm CrossSense that selects themati-

cally interesting objects (that we call pivot objects)

and associates other objects of the folksonomy with

them (that we call the pivot objects world). These

pivot objects and their worlds are presented to the user

to help her in sensemaking in the folksonomy.

KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval

110

We developed an interestingness measure for pivot

objects to be able to decide which objects are more

relevant in sensemaking. In our experiments (on a

Bibsonomy dataset) we showed that, compared to a

baseline, groups of objects associated with the pivot

objects are of greater homogeneity than groups de-

rived from a baseline. Also we showed that with

decreasing interestingness, homogeneity decreases as

well. In another experiment we showed that depend-

ing on type of pivot objects (which may be user, tag

or document), structure of worlds can be completely

different. This shows that it makes a great difference

from which object type a newcomer would like to dis-

cover the folksonomy. Furthermore we could show

that worlds derived by our method differ from each

other, while baseline worlds are similar to each other.

This is desired since the newcomer expects different

worlds describing the folksonomy from different per-

spectives to be different in the objects these worlds

consist of.

REFERENCES

Abdu, E. and Salane, D. (2009). A spectral-based clustering

algorithm for categorical data using data summaries.

In KDD Workshop on Data Mining using Matrices

and Tensors.

Aggarwal, C. C. and Yu, P. S. (2006). A Framework

for Clustering Massive Text and Categorical Data

Streams. In Proceedings of the SIAM conference on

Data Mining 2006.

Banerjee, A., Basu, S., and Merugu, S. (2007). Multi-way

clustering on relation graphs. In SDM.

Begeman, G., Keller, P., and Smadja, F. (2006). Automated

tag clustering: Improving search and exploration in

the tag space. In Proceedings of the WWW’2006

Workshop on Collaborative Web Tagging.

Cattuto, C., Benz, D., Hotho, A., and Stumme, G. (2008).

Semantic grounding of tag relatedness in social book-

marking systems. In ISWC ’08: Proceedings of the

7th International Conference on The Semantic Web,

pages 615–631, Berlin, Heidelberg. Springer-Verlag.

de Gemmis, M., Lops, P., Semeraro, G., and Basile, P.

(2008). Integrating tags in a semantic content-based

recommender. In RecSys ’08: Proceedings of the

second ACM Conference on Recommender Systems,

pages 163–170, Lausanne, Switzerland. ACM.

Golder, S. and Huberman, B. (2006). Usage patterns of

collaborative tagging systems. Journal of Information

Science, 32(2):198–208.

Heymann, P. and Garcia-Molina, H. (2006). Collaborative

creation of communal hierarchical taxonomies in so-

cial tagging systems. Technical report, InfoLab, Com-

puter Science Department, Stanford University.

Hofmann, T. (2001). Unsupervised learning by proba-

bilistic latent semantic analysis. Machine Learning,

42(1):177–196.

Ipeirotis, P., Ntoulas, A., Cho, J., and Gravano, L. (2005).

Modeling and managing content changes in text

databases. In Proceedings of the IEEE Int. Conf. on

Data Engineering (ICDE’05).

Markines, B., Cattuto, C., Menczer, F., Benz, D., Hotho,

A., and Stumme, G. (2009a). Evaluating similarity

measures for emergent semantics of social tagging.

In WWW ’09: Proceedings of the 18th international

conference on World wide web, pages 641–650, New

York, NY, USA. ACM.

Markines, B., Cattuto, C., Menczer, F., Benz, D., Hotho,

A., and Stumme, G. (2009b). Evaluating similarity

measures for emergent semantics of social tagging. In

WWW’09, pages 641–650, Madrid, Spain.

Osinski, S. (2006). Improving quality of search results clus-

tering with approximate matrix factorisations. In Pro-

ceedings of the European Conf. on Information Re-

trieval (ECIR’06), LNCS 3936, pages 167–178.

Sun, J., Tao, D., and Faloutsos, C. (2006). Beyond streams

and graphs: dynamic tensor analysis. In KDD ’06:

Proceedings of the 12th ACM SIGKDD international

conference on Knowledge discovery and data mining,

pages 374–383, New York, NY, USA. ACM.

Symeonidis, P., Nanopoulos, A., and Manolopoulos, Y.

(2010). A uniﬁed framework for providing recom-

mendations in social tagging systems based on ternary

semantic analysis. IEEE Transactions on Knowledge

and Data Engineering, 22(2):179–192.

Zhou, Q., Xu, G., and Zong, Y. (2009). Web co-clustering

of usage network using tensor decomposition. In WI-

IAT ’09: Proceedings of the 2009 IEEE/WIC/ACM In-

ternational Joint Conference on Web Intelligence and

Intelligent Agent Technology, pages 311–314, Wash-

ington, DC, USA. IEEE Computer Society.

CrossSense - Sensemaking in a Folksonomy with Cross-modal Clustering over Content and User Activities

111