
ON THE USE OF CORRESPONDENCE ANALYSIS
TO LEARN SEED ONTOLOGIES FROM TEXT
Davide Eynard, Fabio Marfia and Matteo Matteucci
Dept. of Electronics and Information, Politecnico di Milano, Via Ponzio 34/5, I-20133, Milan, Italy
Keywords:
Ontology learning from text, Knowledge extraction, Correspondence analysis, Machine learning.
Abstract:
In the present work we show our approach to generate hierarchies of concepts in the form of ontologies
starting from free text. This approach relies on the statistical model of Correspondence Analysis to analyze
term occurrences in text, identify the main concepts it refers to, and retrieve semantic relationships between
them. We present a tool which is able to apply different methods for the generation of ontologies from text,
namely hierarchy generation from hierarchical clustering representation, search for Hearst Patterns on the
Web, and bootstrapping. Our evaluation shows that the precision in the generation of hierarchies of the tool
is attested to be around 60% for the best automatic approach and around 90% for the best human-assisted
approach.
1 INTRODUCTION
In the last years there has been a considerable in-
crease in research on knowledge-based systems, es-
pecially in the context of the Semantic Web. How-
ever these systems, as long as they number between
their objectives something more than supplying trivial
functionalities, suffer in their development process of
the so-called knowledge acquisition bottleneck: cre-
ating large, usable, expandable and valid representa-
tions of semantics about a specific domain of interest
represents the most time-consuming task of the whole
project. The cause of this stands in the fact that, be-
ing these structures supposed to represent a collection
of semantics previously unknown to machines, they
need to be manually annotated by domain experts.
Actually, there is already plenty of information
available on the Internet which could be used to
teach a machine about virtually any domain of knowl-
edge: this information is stored in the form of col-
lections of Web pages, large corpora of documents,
databases, and so on. These repositories, however,
cannot be directly consumed by a machine as they
contain unstructured information according to any
standard model for knowledge representation.
One of the main issues in ontology building is
that two different kinds of expertise are required: the
knowledge of the domain that has to be described,
and the ability to encode the ontology in a machine-
interpretable format. Easing this task means either
making semantic technologies more accessible to
domain experts or providing structured information
about a domain to ontology experts. Focusing mainly
on the second part of this problem, our work pro-
vides an alternative to the manual generation of on-
tologies from scratch: automatically extract candidate
concepts and relations from text and suggest a seed
ontology as a first, approximate representation of the
domain knowledge. This ontology can then be mod-
ified (possibly correcting wrong information) and ex-
panded, reducing considerably the time required for
the formalization of the domain knowledge.
The main challenge we face in our tool is the
so called Ontology Learning from Text: free text is
a repository of unstructured knowledge, and this re-
quires researchers to adopt original heuristics in order
to extract structured semantics. These heuristics often
return inaccurate results, and have to be modified and
validated by experts of the domain. Our work aims at
increasing the accuracy of these methods, relying on
different techniques during the main stages of ontol-
ogy learning from text:
• the extraction of the most relevant concepts is per-
formed according to their Information Gain with
respect to a reference corpus of documents;
• subsumption relationships between the identified
concepts are built using three different algorithms
(hierarchy generation from hierarchical clustering
representation, search for Hearst Patterns on the
430
Eynard D., Marfia F. and Matteucci M..
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT.
DOI: 10.5220/0003102204300439
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 430-439
ISBN: 978-989-8425-29-4
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

Web, and bootstrapping);
• the Correspondence Analysis framework has been
employed for the computation of distributional
similarity between terms, which is then used as
a basis to extract different types of relationships.
In Section 2 we present the main approaches to the
problem of the extraction of concept hierarchies that
have been investigated in the context of our project.
In Section 3 we explain in detail the steps of our so-
lution for the extraction of concept hierarchies from
free text. In Section 4 we present a summary of the
results for the tests we performed on the different plu-
gins of our tool. In Section 5 we draw our conclusions
and summarize directions of our future work.
2 ONTOLOGIES FROM TEXT
The extraction of ontologies from text can be super-
vised by a human expert or use any sort of structured
data as an additional source. In the former case, we
are speaking of assisted or semi-automatic learning;
in the latter, we refer to oracle guided learning; if the
algorithm makes no use of structured sources or hu-
man help, it is considered an automatic learner. As an
orthogonal definition, when the objective of the algo-
rithm is the expansion of a pre-constructed ontology
we talk about bootstrapping instead of learning.
A large number of methods for the ontology learn-
ing from text are based on the same conceptual ap-
proach defined Distributional Similarity. It is based
on Harris’ Distributional Hypothesis (Harris, 1968):
“Words are similar to the extent that they
share similar context”.
The idea is to analyze the co-occurrence of words
in the same sentence, paragraph, document, or other
types of context to infer context similarity. The more
two words are similar in their distribution over the
contexts, the more they are expected to be semanti-
cally similar, and the more a potential directed rela-
tion is expected to stand between them.
In Distributional Similarity approaches, concepts
are extracted and organized using some representation
according to their distributional similarity. Then, dif-
ferent methods can be used to identify relationships
between neighbors. ASIUM (Faure D., 1998), for ex-
ample, is a software for the generation of concept hi-
erarchies that uses as context the verb of the sentence
where a concept appears and the syntactical function
(i.e., subject, object, or other complements) of the
concept itself. This tool presents semantically simi-
lar words to the user that can then suggest trough an
interface their hierarchical organization, thus leaving
relations discovery to the user.
Caraballo (Caraballo, 1999) presents an approach
to build a hierarchy of concepts extracted from a cor-
pus of articles from the Wall Street Journal, with the
parser described in (Caraballo and Charniak, 1998).
That model uses as context the paragraph in which
the terms appear, while for the generation of the hi-
erarchy it looks in the text for the so-called Hearst
Patterns (Hearst, 1992). An example for such a pat-
tern is “t
1
s, such as t
2
. . . ”, whose occurrence sug-
gests that term t
2
is a hyponym
1
of term t
1
. A further
different approach is the Learning by Googling one:
Hearst patterns can not only be found within docu-
ment corpora, but they can also be searched on the
Web. PANKOW (Cimiano P., 2004), for instance, is a
software that looks for these patterns on Google and
decides, according to the number of results returned
by the engine, whether a subsumption relation can be
confirmed or denied.
Another model is presented by Fionn Murtagh
in (Murtagh, 2005) and (Murtagh, 2007). This is a
Distributional Similarity approach that relies on Cor-
respondende Analysis (a multivariate statistical tech-
nique developed by J.-P. Benzcri in the ’60s (Benzcri,
1976)) to calculate the semantic similarity between
concepts. The generation of the hierarchy starts from
the assumption that terms appearing in more docu-
ments are more general than others, and the solution
of Murtagh places them in a higher position in the hi-
erarchy.
A strongly different approach from Distributional
Similarity is Formal Concept Analysis, as described
by Philipp Cimiano (Cimiano, 2006). It is based on
different assumptions and largely relies on Natural
Language Processing (NLP) algorithms. The idea in
FCA is to identify the actions that a concept can do
or undergo. Words are organized in groups according
to the actions they share; then groups are ordered in a
hierarchy always according to these actions (i.e. the
group of entities that can run and eat and group of
entities that can fly and eat are put together under the
more general group of entities that can eat). Finally
the user is asked to label every node of the formed
hierarchy (or other automatic methods can be used to
perform this operation), and the final hierarchy is ob-
tained. The paper also describes an algorithm which
generates hierarchies from text by using, as a sort
of prompter, a pre-constructed ontology. What the
model obtains is not an extension of the pre-existent
ontology (as for bootstrapping methods), but a new
1
When a is-a relationship in an ontology starts from
term t
1
and arrives at term t
2
, t
1
is defined as a hyponym
of t
2
, while t
2
is defined as a hypernym of t
1
.
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT
431

and independent one, not necessarily containing all
the entities and relationships of the starting model.
For what concerns bootstrapping approaches,
many methods have been developed which are
based on distributional similarity ((Hearst M.,
1993), (Schutze, 1993), (Alfonseca E., 2002)
and (Maedche A., 2003)). Their common approach
is to evaluate from a corpus of documents the similar-
ity between a word to be added in the ontology and
other words already present in it. Then the algorithms
put the new concept as a son of the concept in the on-
tology that has the more similar children, according
to the similarity information that has been computed.
3 THE EXTRACTION TOOL
For our work, we decided to be based on the concep-
tual model presented by Fionn Murtagh in (Murtagh,
2005) and (Murtagh, 2007). The main steps of our
approach are depicted in Figure 1.
3.1 Data Indexing
To reduce the complexity of the problem, we start by
selecting a set of terms that can be considered as the
more relevant for the document corpus. To do this
we start from two corpora of documents: the training
corpus, which is used as a referential corpus by the
procedure of identification of the relevant terms, and
the test corpus, that is the main corpus from which the
terms are to be extracted and the ontology has to be
learned.
To allow our application to rapidly handle the doc-
uments and the terms contained within them, our first
task is to index the two document corpora. To perform
this operation we used Lucene
2
, which takes care of
tokenization, indexing, and stopwords filtering. The
indexing process is usually very time-consuming, so
users are allowed to save the indexes generated and
reuse them across different executions.
3.2 Data Filtering
Moreover, during the indexing phase, filters can be
applied in order to select terms according to specific
needs: two different filters (one based on Wordnet
and the other on NLP algorithms) can be used to dis-
card everything but the nouns, while another one au-
tomatically discards terms composed by less than n
letters (usually, very short terms rarely represent rele-
vant concepts, even if there are some exceptions such
as with acronyms).
2
http://lucene.apache.org
3.3 Identification of Relevant Terms in
the Test Corpus
For every term appearing in the test corpus the score
of Information Gain is computed. Information Gain
measure is based on the concept of entropy. In our
case, we want to calculate how the total entropy
changes for the two training and test corpora by know-
ing that a specific term is more or less common within
these sets. We can identify the P(i) function as the
probability for a document to appear in a corpus i,
computed as the number of the documents in i divided
by the total number of documents:
p(i) =
documentsIn(i)
totalDocuments
(1)
Where i can be training or test. Our entropy measure
for a group of documents D
g
distributed in the two
corpora is measured as:
H
D
g
= −
∑
i
p(i) · log(p(i)) (2)
We identify three different groups of documents:
• the group of all documents, D
total
;
• documents presenting the term of interest t in
them, D
t
;
• documents not presenting the term of interest t in
them, D
¬t
.
Information Gain score of term t is then calculated as:
IG(t) = H
D
total
−
|D
t
|
|D
total
|
H
D
t
−
|D
¬t
|
|D
total
|
H
D
¬t
(3)
Information Gain returns low values for terms that
are very common in both training and test corpora.
Terms that, instead, are very common in just one of
the two corpora make Information Gain return high
results. In this context, the training corpus has the role
of a reference for the test corpus: terms that are fre-
quent in test corpus can both be characterizing terms
of the corpus, or very useless terms as conjunction,
common adverbs, common verbs. If a term t is very
frequent also in the training corpus, which refers to a
topic different from the test corpus, t is supposed to
be a useless term, and, in fact, it will receive a lower
IG value. Vice versa, if t is very frequent in test cor-
pus, but not in training corpus it is supposed to be a
characterizing term of the test corpus, and in fact, it
will receive a higher IG value.
At the end, a set of n (with n specified by the user)
relevant terms is collected, as the top n terms of the
IG rank.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
432

INPUT:
Training and test
Document corpora
Data
filtering
Similarity
computation
through CA
Indexing
Identification
of relevant terms
in test corpus
Creation
of the
hierarchy
OUTPUT:
final hierarchy
in
at
kingdom
troop
Murtagh Algorithm
HP on Web
Bootstrapping
HP+Bootstrapping
Figure 1: Main steps of our approach for ontology learning from text.
Figure 2: An example of Correspondence Analysis 2-dimensional projection, from a corpus of documents about the Roman
Empire.
3.4 Similarity Computation through
Correspondence Analysis
The approach of Correspondence Analysis (Murtagh,
2005) is used to project the relevant terms in
a k-dimensional Euclidean space
3
according to
3
k can be chosen at will by the user: the more the di-
mensions, the higher the precision of the distances in the
representation.
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT
433
their distributional behavior over the documents.
Correspondence Analysis starts from a (test
documents)×(relevant terms) matrix, where the
cell n
i, j
holds the number of occurrences of the jth
term in the ith document, as, for example:
caligula city group
D1 60 12 60
D2 20 54 5
D3 32 3 2
D4 1 2 5
In order to create the Euclidean space, Corre-
spondence Analysis operates over the matrix differ-
ent transformations. The first step is to calculate the
grand total of the individual observations and divide
each number in the cells for this grand total. This is
done in order to have a matrix M
prob
expressing in the
n
i, j
cell the probability of co-occurrence of the two
(i, j) modalities (i.e., documents and terms). In this
simple example, the grand total is 376, and the prob-
ability matrix results:
M
prob
caligula city group
D1 0.159 0.031 0.159
D2 0.053 0.143 0.013
D3 0.085 0.007 0.005
D4 0.002 0.005 0.332
Then the sums of the values of each row and each
column are computed; we call the sum of the values
of the ith row F
i
and the sum of the values of the jth
column F
j
. These are the marginal distributions of the
two modalities:
M
prob
eat city group F
i
D1 0.159 0.031 0.159 35%
D2 0.053 0.143 0.013 21%
D3 0.085 0.007 0.005 10%
D4 0.002 0.005 0.332 34%
F
j
30% 19% 51%
Being
∑
i
n=0
F
i
= 1 and
∑
j
n=0
F
j
= 1, we prefer to re-
port F
i
and F
j
as percentages, every percentage repre-
sents the contribution of the ith or jth modality to the
total of the occurrences. Now we proceed by gener-
ating the so-called matrix of column profiles. Let us
consider the columns of our M
prob
matrix; the algo-
rithm divides every n
i, j
probability by the F
j
value.
What we obtain is the matrix whose columns are
called column profiles:
M
col pro f
caligula city group F
i
D1 53% 17% 31% 35%
D2 18% 76% 3% 21%
D3 28% 4% 1% 10%
D4 1% 3% 65% 34%
Column profiles are a very important element of
Correspondence Analysis because they represent the
pure distributional behavior of column modalities (the
terms, in our case), independently from the original
amount of occurrences we were dealing with.
The last F
i
column represents the average behavior
of the different column profiles. The divergences of
the single column profiles from this average profile
can be measured with the χ
2
test of independence, and
the χ
2
distance between the l column profile and k
column profile can be computed as:
χ
2
(l, k) =
s
∑
j
(n
l, j
− n
k, j
)
2
F
j
. (4)
The sum of all the χ
2
tests applied to all column
profiles in respect to the average profile represents the
total inertia of the matrix in respect to his columns.
Inertia represents the total amount of divergence of
the column profiles from the assumption of indepen-
dence. The higher is this number, the higher is the
probability of an interdependence between rows and
columns. There is also something more to say about
the χ
2
distance between two different column profiles:
the obtained value represents how much two differ-
ent rows diverge in their distributional behavior; the
more similar this behavior is, the more there should
be a similarity between the entities represented by the
two columns (in our case these entities are the terms
appearing in documents).
What Correspondence Analysis does, starting
from the column profiles matrix, is to provide a sum-
mary representation of the similarities between the
column modalities. In order to do so we project them
into an Euclidean space of k dimensions, where:
k = min(i − 1, j − 1) (5)
This space has the following properties:
• the Euclidean distance between the column
modalities in this space of representation is ex-
actly equal to the χ
2
distance between their col-
umn profiles; calling the αth dimension of the jth
column F
α
( j) we can state:
χ
2
(l, k) =
s
∑
i
(n
i,l
− n
i,k
)
2
F
i
=
r
∑
α
(F
α
(l) − F
α
(k))
2
(6)
• the origin of the axis is placed in the barycenter of
the different column profiles in respect to the χ
2
distance measure, that is, as we said, the average
column profile
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
434
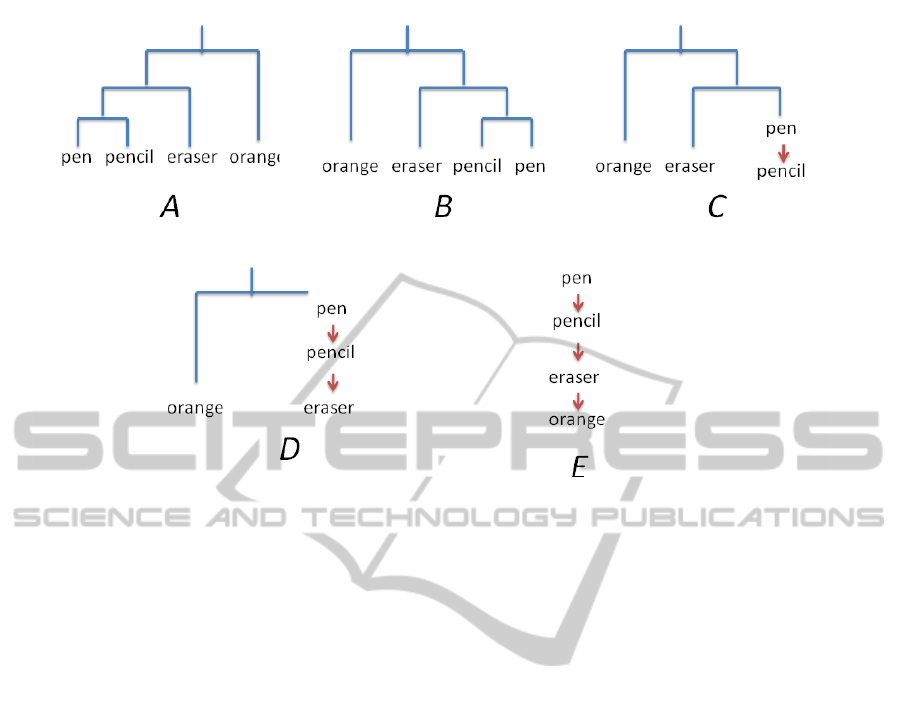
Figure 3: Simple example of Hierarchy generation, according to Fionn Murtagh’s approach.
• axes are selected to have along them, in decreas-
ing order from the first to the kth, the maximum
possible variance of the projected elements
The creation of the space is done with the appli-
cation of different operations over the column profiles
matrix, the most important between them is a eigen-
value decomposition applied to translate the cloud of
modalities into a different referential system where
the axes are organized along the directions of maxi-
mum distribution of the points.
Knowing that the axes are ordered according to
the variance of the elements, if we want to reduce the
complexity of the representation, we can just discard
as many dimensions as we want, starting from the last
one. In this way, we know that we keep always the
dimensions with the highest distribution, so, the di-
mensions carrying the higher amount of distributional
information. Plot in Figure 2 was obtained just keep-
ing the 2 most important axes in the k-dimensional
space created.
3.5 Creation of the Hierarchy
At this step the user of our Extraction tool can choose
among different algorithms to be applied for the cre-
ation of the hierarchy. The options are four:
• Murtagh’s Algorithm.
• Hearst Patterns on Web.
• Maedche and Staab’s Bootstrapping.
• An original combination of the last two.
3.5.1 Murtagh’s Algorithm
This approach applies the technique presented by
Fionn Murtagh in (Murtagh, 2007) for the generation
of a hierarchy of concepts from a hierarchical clus-
tering representation. Having used the Correspon-
dence Analysis technique, adopted in many works by
Fionn Murtagh, it was natural for us to experiment
with his solution for the generation of hierarchies of
concepts, although better results can be obtained with
other techniques.
A Hierarchical Clustering tree is created defining
the terms proximities in the tree according to their
proximity in the Euclidean space. The algorithm
starts from this representation to build the concept hi-
erarchy (see Figure 3, A), ordering clusters from right
to left according to their proximity to the origin in the
k-dimensional representation. This is done because
terms appearing closer to the origin are expected to
be more general terms, being their occurrences dis-
tributed over the maximum number of documents. In
our case, the representation is exactly specular to what
we had (Figure 3, B).
Starting from the first created cluster, the right sib-
ling is always considered as a hyponym of the left one.
Thus, in our example, pen would be considered as a
hypernym of pencil (Figure 3, C). Again, the right
siblings, pen and pencil, are hypernyms of the left
one, eraser (Figure 3, D). Finally, pen, pencil and
eraser are hypernyms of orange (Figure 3, E). This
final representation is returned as the searched hierar-
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT
435

Figure 4: Example of Hierarchical Clustering of terms ex-
tracted from the 2-dimentional projection of the corpus
about the Roman Empire of Figure 2.
chy. An example of a Hierarchical Clustering tree
extracted from Correspondence Analysis depicted in
Figure 2 is shown in Figure 4.
3.5.2 Hearst Patterns on Web
The Hearst Patterns on Web approach can be applied
both for the creation of a hierarchy from scratch or
to expand an existing one. We created this solution
taking inspiration from the application PANKOW and
the general principles of Learning by Googling.
The algorithm starts with a hierarchy to be ex-
panded (bootstrapping), or with a empty hierarchy if
we want to create a new one. In the latter case, the
first term t
1
to be added is simply put under the root
element. Then, for every new term t
n
to be added, its
lokelihood to be an hyponym of any term t
i
already in
the hierarchy is checked as follows:
1. five different pre-defined strings based on Hearst
patterns are built:
• hp
1
: pluralize(t
i
) such as t
n
• hp
2
: pluralize(t
i
) including t
n
• hp
3
: pluralize(t
i
) especially t
n
• hp
4
: pluralize(t
i
) like t
n
• hp
5
: t
n
is a/an t
i
2. six Google queries are executed (the five Hearst
patterns plus the single term t
n
), obtaining the
number of Google hits for each query
3. the score of every string is defined as the ratio be-
tween the number of its Google hits and the num-
ber of Google hits of the hyponym searched alone
score
hp
i
=
googleHits(hp
i
)
googleHits(t
n
)
(7)
4. the total score is obtained as a sum of the different
five scores
Once the hypernymy scores have been calculated
for every t
i
in the hierarchy, t
n
is placed as hy-
ponym of the t
i
with the highest score between all the
scores, provided that it exceeds a pre-defined thresh-
old level
4
.
If no t
n
hypernyms exceed the threshold level, the
user can possibly suggest a hypernym manually. She
can also select to discard the term or to add it in the
hierarchy as a hyponym of the root element. The al-
gorithm can also be executed in its automatic mode,
in this case it directly puts the t
n
term as a hyponym
of the root element.
After t
n
is placed, all its siblings are checked in the
same manner for an hyponymy relation with t
n
; if the
relation surpasses the threshold, the sibling element is
put as a hyponym of t
n
.
3.5.3 Maedche and Staab’s Bootstrapping
Maedche and Staab’s Bootstrapping Process is an in-
stantiation of the model defined by A. Maedche and S.
Staab in (Maedche A., 2003). In this model, a concept
hierarchy is expanded adding a new t
n
term accord-
ing to the hypernyms of its m nearest neighbors in the
k-dimensional space, where m is a parameter of the
algorithm. The score for every f candidate hypernym
is calculated as follows.
The Least Common Superconcept between two
concepts a and b in a hierarchy is defined as:
lcs(a, b) = argmin
c
δ(a, c) + δ(b, c) + δ(root, c), (8)
where δ(a, b) is the distance between a and b in terms
of the number of edges which need to be traversed.
Then the taxonomic similarity σ between two con-
cepts in a hierarchy can be defined:
σ(a, b) =
δ(root, c) + 1
δ(root, c) + δ(a, c) + δ(b, c) + 1
, (9)
where c = lcs(a, b). The W ( f ) score for a certain can-
didate hypernym f is finally computed as:
W ( f ) =
∑
h∈H( f )
sim(t
n
, h) · σ(n, h), (10)
where t
n
is the term to be classified and H( f ) is the set
of hyponyms of candidate hypernym f that are also
nearest neighbors of t
n
in the k-dimensional space.
4
The threshold level was empirically identified after few
experiments.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
436

The sim function is the similarity between two con-
cepts as obtained from the k-dimensional space.
If no t
n
hypernyms are found, the user can possi-
bly suggest a hypernym manually. She can also select
to discard the term or to add it in the hierarchy as a hy-
ponym of the root element. The algorithm can also be
executed in its automatic mode: in this case, it directly
puts the t
n
term as a hyponym of the root element.
3.5.4 Combination of Hearst Patterns on Web
and Bootstrapping Algorithms
This approach works by combining the two previous
algorithms we described for expanding a hierarchy.
The pre-existing hierarchy could be huge, and a new
t
n
term to be added with the Hearst patterns algorithm
would generate a huge amount of connections to the
Google servers. Depending on the Internet connec-
tion speed, the execution of a very large number of
HTTP requests could be very time consuming.
In this case, we look for the n nearest neighbors in
the k-dimensional space of t
n
in the pre-existing hier-
archy, and collect all their ancestors. These ancestors
are considered the candidate hypernyms of t
n
and they
are checked according to the Hearst Patterns on Web
algorithm.
If no hypernyms are found, the user can possibly
suggest a hypernym manually. She can also select to
discard the term or to add it in the hierarchy as a hy-
ponym of the root element. The algorithm can also be
executed in its automatic mode, in this case it directly
puts the t
n
term as a hyponym of the root element.
4 TESTS AND RESULTS
We evaluated the precision of the ontologies gen-
erated by some of the automatic and assisted algo-
rithms, defined as the ratio between the right relation-
ships (as evaluated by a human judge) and the totality
of the relationships found:
precision =
right relationships
total relationships in ontology
(11)
Three different corpora of documents were se-
lected as test corpora:
• a set of 847 Wikipedia articles about Artificial In-
telligence and related arguments;
• a set of 1464 Wikipedia articles about Roman
Empire and related historical articles;
• a set of 1364 Wikipedia articles about Biology.
As a referential Training corpus we always use
the same collection of 1414 Wikipedia articles about
Wikipedia itself. This choice was made according
to what we stated about the Information Gain mea-
sure for term relevance: we expected from the com-
parison between any of the three test corpora and this
Wikipedia training corpus that less importance would
have been given to terms typical of every Wikipedia
article. This, in fact, proved to be correct and terms
as “Wikipedia”, “Wikimedia”, or “article”, that have
a high frequency in all the four corpora of documents,
received a lower Information Gain value with respect
to other characterizing terms of each test corpus.
We then applied the Correspondence Analysis al-
gorithm in order to generate a 2-dimensional repre-
sentation of distributional similarity of the relevant
terms, starting from this representation to execute the
different ontology learning algorithms described in
this paper. In Table 1 the average precision measures
of the ontologies obtained from the application of the
algorithms are summarized.
While Murtagh’s algorithm does not seem to per-
form well, the research for Hearst patterns via Web
seems to be a good option for the generation of con-
cept hierarchies. Its semi-automatic version provides
nearly ready-to-go ontologies, producing hierarchies
such as the one depicted in Figure 5.
Maedche and Staab’s Bootstrapping algorithm
and its combination with Hearst Patterns on Web al-
gorithm were designed to expand large concept hi-
erarchies, and, as we did not have one available, no
valid attempts have been done to test them. Early
tests with small ontologies, anyway, showed that the
combination of Maedche and Staab’s algorithm with
Hearst Patterns on Web improves the precision of
Maedche and Staab’s algorithm alone of about 10%,
but these should be considered as preliminary results
so are not reported in this paper.
5 CONCLUSIONS
In this paper we presented Extraction, a tool for the
generation of seed ontologies from text. Addressing
the problem of ontology extraction from text, we de-
veloped a modular system whose main advantage, in
our opinion, is the original co-presence of the follow-
ing three features:
• a pre-process of identification of relevant terms,
which relies on the calculation of information gain
to reduce the complexity of the following elabo-
ration steps;
• the strong framework of correspondence analysis
for the computation of distributional similarity be-
tween terms;
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT
437

Table 1: Precision measures obtained from the evaluation of the different ontology learning algorithms.
Algorithm AI Rome Biology Average
Murtagh 6.6% 5.22% 1.87% 4.56%
Hearst Patterns on Web 60.00% 75.00% 37.50% 57.50%
Hearst Patterns on Web (assisted) 90.00% 94.52% 85.07% 89.86%
Figure 5: A hierarchy created by the Hearst Patterns on Web algorithm in its semi-automatic procedure, from 100 terms of a
corpus about the Roman Empire.
• the possibility to use different algorithms for the
generation of ontologies.
The results of our evaluation are promising. The
tool surely represents an evolution and an improve-
ment in performance with respect to Murtagh’s ap-
proach, that uses an algorithm for the generation of
hierarchies which strongly depends on an inherent
characteristic of texts called ultrametricity (Murtagh,
2007), condition which does not appear to be met in
the documents that we have analyzed. The assisted
Hearst patterns method, despite of having the disad-
vantage of requiring user interaction, provides high-
quality hierarchies which are almost ready to use. Fi-
nally, the tool allowed us to combine different algo-
rithms and provide qualitatively better results, such
as in the case of Maedche and Staab’s plus Hearst pat-
terns.
As a negative note, while making the tool more
powerful by adding functionalities based on NLP we
also made it more dependent on a specific language.
This is a limitation if we compare our approach to
Murtagh’s, as pure correspondence analysis is lan-
guage independent. However, this limit is some-
how counterbalanced by the advantages that NLP pro-
vides, such as the possibility of filtering extracted
concepts by keeping only names without the need to
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
438

rely on a limited vocabulary like Wordnet. Similarly,
the extraction of concepts with information gain de-
pends on the set of documents that is chosen as a
training corpus: while this obviously looks like a lim-
itation, it also has useful drawbacks like in our eval-
uation, when we were able to use a set of general
Wikipedia documents to automatically filter all the
Wikipedia-related text from the articles we wanted to
study.
For what concerns possible future improvements
to our project, we would like to continue our work in
two main directions: on the one hand, improving our
evaluations by testing our tool with large ontologies
(especially while using the bootstrapping algorithm)
and comparing its results with the ones obtained by
using other algorithms; on the other hand, improving
the application itself by adding new functionalities
and a better user interface to easily configure them.
REFERENCES
Alfonseca E., M. S. (2002). Extending a lexical ontology by
a combination of distributional semantics signatures.
In Proceedings of the 13th International Conference
on Knowledge Engineering and Knowledge Manage-
ment.
Benzcri, J.-P. (1976). L’Analyse des Donnes. Dounod.
Caraballo and Charniak (1998). New figures of merit for
best-first probabilistic chart parsing. In Computa-
tional Linguistics.
Caraballo, S. (1999). Automatic construction of a
hypernym-labeled noun hierarchy from text. In Pro-
ceedings of the 37th Annual Meeting of the Associa-
tion for Computational Linguistics.
Cimiano, P. (2006). Ontology Learning and Population
from Text. Springer.
Cimiano P., Handschuh S., S. S. (2004). Towards the self-
annotating web. In Proceedings of the 13th World
Wide Web Conference.
Faure D., N. C. (1998). A corpus-based conceptual cluster-
ing method for verb frames and ontology. In Proceed-
ings of the LREC Workshop on Adapting lexical and
corpus resources to sublanguages and applications.
Harris, Z. (1968). Mathematical Structures of Language.
Wiley.
Hearst, M. (1992). Automatic acquisition of hyponyms
from a large text corpora. In Proceedings of the 14th
International Conference of Computational Linguis-
tics.
Hearst M., S. H. (1993). Customizing a lexicon to better
suit a computational task. In Proceedings of the ACL
SIGLEX Workshop on Acquisition of Lexical Knowl-
edge from Text.
Maedche A., Pekar V., S. S. (2003). On discovering taxo-
nomic relations from the web. Technical report, Insti-
tute AIFB - University of Karlsruhe, Germany.
Murtagh, F. (2005). Correspondence Analysis and Data
Coding with Java and R. Chapman & Hall.
Murtagh, F. (2007). Ontology from hierarchical structure in
text. Technical report, University of London Egham.
Schutze, H. (1993). Word space. In Advances in Neural
Information Processing Systems 5.
ON THE USE OF CORRESPONDENCE ANALYSIS TO LEARN SEED ONTOLOGIES FROM TEXT
439
