AN MOEA-BASED METHOD TO TUNE EA PARAMETERS

ON MULTIPLE OBJECTIVE FUNCTIONS

S. K. Smit, A. E. Eiben and Z. Szl´avik

Department of Computer Science, VU University Amsterdam, de Boelelaan 1081, Amsterdam, The Netherlands

Keywords:

Parameters, Evolutionary algorithms, Multi-function tuning, Parameter tuning.

Abstract:

In this paper, we demonstrate the beneﬁts of using a multi-objective approach when tuning the parameters of

an Evolutionary Algorithm. To overcome the speciﬁc challenges that arise when using a meta-algorithm for

parameter tuning on multiple functions, we introduce a new algorithm called the Multi-Function Evolutionary

Tuning Algorithm (M-FETA) that is able to approximate the parameter Pareto front effectively. The results of

the experiments illustrate how the approximated Parameter Pareto front can be used to gain insights, identify

‘generalists’, and study the robustness of the algorithm to be tuned.

1 INTRODUCTION

In recent years there has been a growing interest

in automated parameter tuning methods in Evolu-

tionary Computing (EC). New tuning algorithms,

such as SPO (Bartz-Beielstein et al., 2005; Bartz-

Beielstein and Markon, 2004; Bartz-Beielstein et al.,

2004), REVAC (Nannen and Eiben, 2006; Smit and

Eiben, 2009), and Meta-ES (Yuan and Gallagher,

2007), have been developed and shown their success.

Their ability of ﬁne-graining the search in the most

promising areas of the parameter space makes them

suited for users only in need for good parameter val-

ues. Traditional methods, as Design of Experiments

(DoE), often require huge computational efforts, te-

dious manual testing or a combination of both, and

are therefore less suited for such ‘lazy’ users. This

paper is concerned with a generalization of these kind

of tuning algorithms from tuning an Evolutionary Al-

gorithm (EA) on a single objective function, to tuning

an EA on a set of objective functions. In standard EC

terms, we are interested in robust parameter values

that make the EA that uses them a ‘generalist’, rather

than a ‘specialist’.

Identifying robust parameter values for a given

test suite is a non-trivial problem. A straightforward

approach is to deﬁne a preference vector containing

a weight for each function in the test suite and apply

a tuning algorithm to maximize the weighted average

of performances. In other words, a linear combina-

tion of the performances is maximized as a single-

objective optimization problem. However, as shown

in (Smit and Eiben, 2010), this approach runs into cer-

tain problems if the test suite contains ﬁtness func-

tions with different levels of difﬁculty (and most test

suites do). In particular, the tuner will favor parameter

values driven by performance on the hard test func-

tions, thus introducing a bias that is not intuitive for

a common user. Alternatives to this simple approach

can be sought by looking at the multi-function tun-

ing problem as a multi-objective optimization prob-

lem. This view is quite natural: each ﬁtness function

in the test suite corresponds to one objective. To be

precise, the EA performance on a test function is an

objective function to be maximized, hence a test suite

of M ﬁtness functions induces a multi-objective opti-

mization problem with M objectives.

Making the step to the ﬁeld of multi-objective op-

timization implies that we can beneﬁt from the whole

body of knowledge of this ﬁeld (Deb, 2001). In

particular, instead of reinventing the wheel, we can

adopt the common techniques from multi-objective

optimization algorithms, adjust it to the speciﬁc cir-

cumstances of tuning EA parameters and investigate

whether and to what extent it can be used as a multi-

function tuner. Notice, that this question about ap-

plicability is not as trivial as it may seem, because

tuning brings forward speciﬁc challenges. Firstly, the

stochastic nature of EAs to be tuned causes inherently

noisy measurements on the objectives. Secondly, the

large amount of tests required for a good result im-

plies impractical computational efforts.

When selecting a multi-objective optimization al-

gorithm we have two preferences. First, we have a

261

K. Smit S., E. Eiben A. and Szlávik Z..

AN MOEA-BASED METHOD TO TUNE EA PARAMETERS ON MULTIPLE OBJECTIVE FUNCTIONS.

DOI: 10.5220/0003106202610268

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 261-268

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

preference for an evolutionary method, based on the

large number of successful multi-objective evolution-

ary algorithms in the literature (Deb et al., 2002; Zit-

zler et al., 2001). Second, we want to have an algo-

rithm that produces the Pareto front of non-dominated

points in the search space (here: the space of parame-

ter vectors of the EA to be tuned). This preference is

motivated by the advantages this approach offers, e.g.,

it allows us to investigate interactions between ﬁtness

functions, parameter values, and the evolutionary al-

gorithm. Furthermore, it allows us to identify various

‘generalists’ rather than a single one, as well as to an-

alyze the robustness of an EA.

The main contributions of this paper can be listed

as follows.

• We introduce a multi-function tuning algorithm

called M-FETA based on a Multi-Objective Evo-

lutionary Algorithm (MOEA) approach that is

able to cope the two principal challenges men-

tioned above.

• We demonstrate the beneﬁts of using an approxi-

mated Pareto front by tuning an EA on the Sphere

and Rastrigin functions.

Namely, the parameter

Pareto front allows us to investigate interactions

between ﬁtness functions, parameter values, and

the evolutionary algorithm. Furthermore, it allows

to identify different kinds of ‘generalists’ rather

than a single one, as well as to analyze the robust-

ness of an EA.

2 PARAMETERS, TUNERS, AND

UTILITY LANDSCAPES

In general, one can distinguish three layers in param-

eter tuning: the application layer, the algorithm layer,

and the design or tuning layer. The whole scheme can

be divided into two optimization problems. The lower

part of this three-tier hierarchy consists of a problem

on the application layer (e.g., the traveling salesman

problem) and an EA (e.g., a genetic algorithm) on the

algorithm layer trying to ﬁnd an optimal solution for

this problem. Simply put, the EA is iteratively gen-

erating candidate solutions (e.g., permutations of city

names) seeking one with maximal quality. The upper

part of the hierarchy contains a tuning method that

is trying to ﬁnd optimal parameter values for the EA

on the algorithm layer. Similarly to the lower part,

A test suite of 2 functions is certainly not large

(enough), but here we are mainly interested in a proof-of-

concept and demonstrating the new technology, rather than

real tuning on an ‘interesting’ test suite.

the tuning method is iteratively generating parame-

ter vectors seeking one with maximal quality, where

the quality of a given parameter vector ¯p is based on

the performance of the EA using the values of it. To

avoid confusion we use distinct terms to designate the

quality function of these two optimization problems.

Conform the usual EC terminology we use the term

ﬁtness for the quality of candidate solutions on the

lower level, and the term utility to denote the quality

of EA parameter vectors.

In simplest case, the utility of a parameter vec-

tor ¯p is the performance of the EA using the values

of ¯p on a given test function F. Tuning an EA (by

whichever performance metric) on one single func-

tion F delivers a specialist, that is, an EA that is very

good in solving F with no claims or indications re-

garding its performance on other problems. This can

be a satisfactory result if one is only interested in solv-

ing that given problem. However, algorithm design-

ers in general, and evolutionary computing experts in

particular, are often interested in so called ‘robust pa-

rameter values’, that is, in parameter values that make

an EA using them work well on many problems. To

this end, test suites consisting of many test functions

are used to evaluate algorithms and to support claims

that a given algorithm is good on a ‘wide range of

problems’. This approach raises serious methodol-

ogy issues as discussed in (Eiben and Jelasity, 2002),

and may also be in conﬂict with theoretical results, cf.

(Wolpert and Macready, 1997), all depending on how

the claims are formulated. In this paper we do not

elaborate on these issues, but take a pragmatic stance

instead: We are after a method that is able to ﬁnd pa-

rameter vectors that work well on a given set of test

functions.

3 MULTI-FUNCTION

EVOLUTIONARY TUNING

ALGORITHM

The Multi-Function Evolutionary Tuning Algorithm

(M-FETA) is, in essence, a Multi-Objective Evolu-

tionary Algorithm with a particular technique of as-

sessing the quality of candidate solutions. This tech-

nique is designed for being used within a parameter

tuner for EAs. In such applications candidate solu-

tions are EA parameter vectors whose quality is de-

ﬁned by the performance of the EA on a collection

of functions F = { f

, . . . , f

}. By the stochastic na-

ture of EAs, this performance is a noisy observable.

In tuning terms, this means that the utility of a pa-

rameter vector ¯x can only be estimated. The usual

ICEC 2010 - International Conference on Evolutionary Computation

262

way of improving these estimates is to repeat the mea-

surements(Hughes, 2001; University and Fieldsend,

2005; Eskandari and Geiger, 2009; Deb and Gupta,

2005), that is, to do more EA runs using ¯x, but this is

clearly an expensive way of gaining more conﬁdence.

The main idea behind our technique is to do just one

run with each parameter vector ¯x and to improve the

conﬁdence by looking at the utilities of similar param-

eter vectors in our archive, assessed before.

To this end, we use the concept of neighborhoods,

as proposed in (Branke, 1998). The neighborhood N

¯x

of the parameter vector ¯x is deﬁned as the k individu-

als from the archive with the smallest Euclidean dis-

tance to ¯x. These neighbors are used to ‘conﬁrm’ the

utility of ¯x. In contrast to (Branke, 1998), we apply a

t-test with a conﬁdence level of (1−M · α) in to com-

pare two parameter vectors ¯x and ¯y. In order to evalu-

ate their dominance, the 2· k data points showing the

EA performance of these parameter vectors in N

¯x

and

¯y

, respectively, are tested for a signiﬁcant difference

in performance on each of the functions. To be pre-

cise, we say that certain parameter vector ¯x dominates

parameter vector ¯y if, and only if:

1. ∃ f ∈ F such that the performance of the EA on f

based on the data belonging to N

¯x

is signiﬁcantly

better than the performance based on the data

belonging to N

¯y

and

2. ∀g ∈ F(g 6= f) the performance of the EA on g

for vectors in N

¯y

is not signiﬁcantly better than

the performance for vectors in N

¯x

Based on dominance, we can rank parameter vec-

tors in many ways. Here we have choose for the com-

putationally least extensive measure, namely the rank

¯x

of ¯x is deﬁned as the number of vectors that dom-

inate ¯x divided by 2 · k and then rounded down. This

measure ensures that vectors with a similar number of

dominating points receive the same rank.

Now we use ranking to compare and order param-

eter vectors. We consider a certain parameter vector ¯x

better than a parameter vector ¯y if, and only if:

1. ¯x has a lower rank than ¯y, or

2. ¯x and ¯y have the same rank, but ¯x is more isolated

than ¯y

In fact, we rely on a form of the strong causality prin-

ciple, stating that small changes to a parameter vector cause

only small changes in its utility.

This deﬁnition is less strict than in (Eskandari and

Geiger, 2009)

where ¯x is more isolated than ¯y iff, it is farther away

from its neighbors than ¯y:

∑

¯z∈N

¯x

d(¯x, ¯z) >

∑

¯z∈N

¯y

d(¯y, ¯z)

There are two important properties of this system

from the perspective of sampling new parameter vec-

tors for being tested. The ﬁrst property is an inher-

ent bias towards preferring isolated vectors as par-

ents in M-FETA. This bias comes from the fact that

if the neighbors of a certain vector are too far, then

the standard-deviation of EA performance results in

¯x

is large. Large standard-deviations cause a t-test to

indicate ‘no signiﬁcant difference’, which then lowers

the number of dominating vectors, and therefore de-

creases the rank. This, in turn, increases probability

of being selected for reproduction.

The second property is true (or at least assumed)

in the majority of reproductive systems and can be

popularized as “the apple does not fall far from its

tree”. In technical terms, this means that child vec-

tors of ¯x are likely to be close to ¯x. In the end,

this decreases the distances in its neighborhood, and

therefore sharpens the estimate of its utility. On the

other hand, if a certain vector with a high standard-

deviation already performs signiﬁcantly worse than

other vectors, then no effort is invested into re-

evaluating it, an effect similar to racing (Maron and

Moore, 1997). This makes that the algorithm only

spends time on reﬁning estimates and investigating

new points in promising areas, thus limiting the com-

putational efforts.

4 PARAMETER PARETO

FRONTS

The parameter Pareto set is formed by all parameter

vectors that are non-dominated, i.e., for which there is

no other parameter vector that performs signiﬁcantly

better on one of the test functions, and at least as good

on the other functions. Each vector in the Pareto set

can therefore be seen as ‘robust’, but they all repre-

sent a different trade-off regarding the performance

on different test functions. Which is the most prefer-

able point on this front, is subject to particular user

preferences, for example:

1. The one with a maximum performance if all ob-

jectives have equal weights.

2. The one with the best performance on problem F

while maintaining a given level of minimum per-

formance on F

AN MOEA-BASED METHOD TO TUNE EA PARAMETERS ON MULTIPLE OBJECTIVE FUNCTIONS

263

0 0.25 0.5 0.75 1

0.25

0.5

0.75

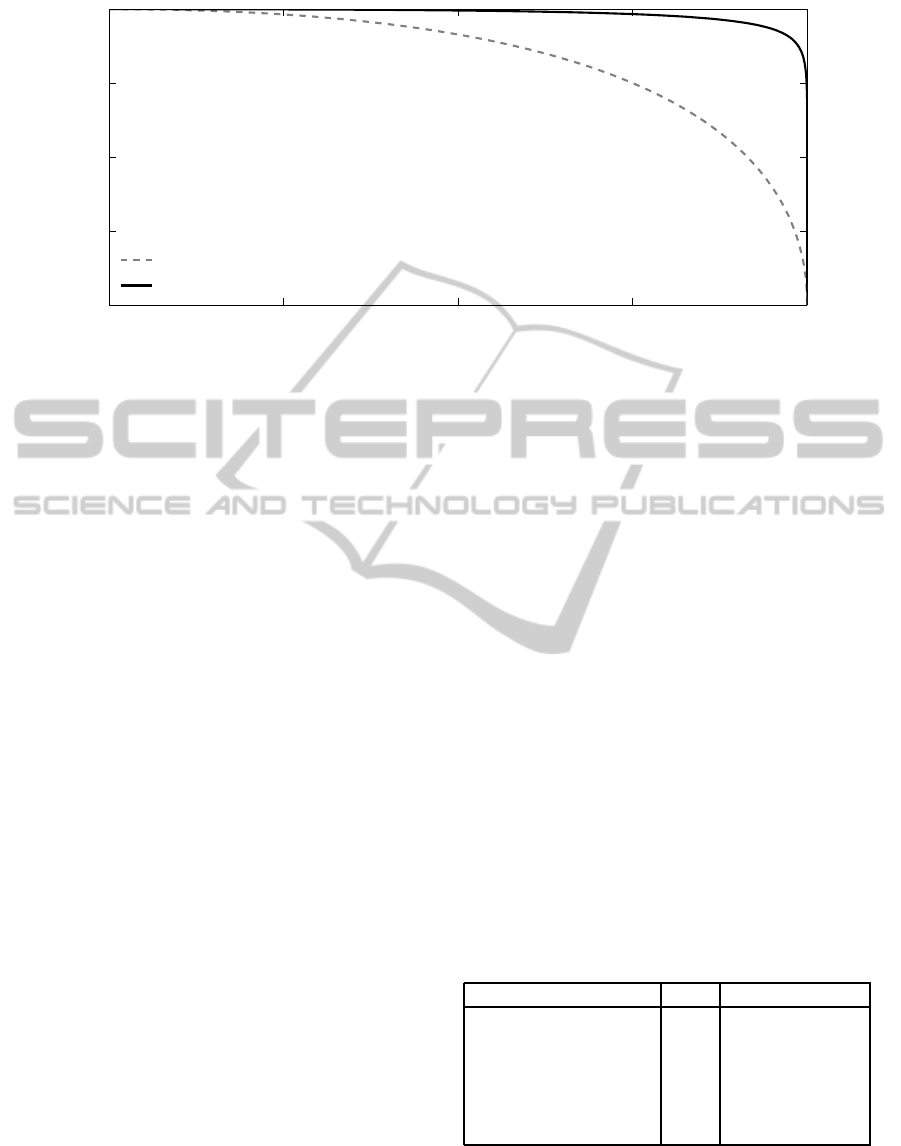
Figure 1: The parameter Pareto fronts of a robust and a not robust algorithm.

In principle, single-function tuning could be used

(with some tweaks) to solve both of these example

cases. However, a multi-function approach using a

parameter Pareto front has additional advantages be-

cause of the various non-dominated options it offers.

For instance, in the ﬁrst case one could discover that

by just a slight shift in preferences one can reach a

much better performance on F

without losing too

much performance on F

. Similarly for the second

case, an inspection of the Pareto front can disclose

that slight decrease in the performance threshold for

can yield a great increase in performance on F

Furthermore, parameter Pareto fronts can also be

used for the evaluation of algorithms. To this end, one

needs to consider the whole Pareto front that exhibits

information on the algorithm itself. (While one point

on the Pareto front only says something about the pa-

rameter vector it belongs to.) Figure 1 illustrates this

matter by showing the imaginary Pareto fronts of two

algorithms A and B. The x and y axes correspond to

test functions F

and F

, respectively, and we assume

that EA performance on both test functions is to be

maximized. Each dot in the graph belongs to a pa-

rameter vector ¯p with the obvious convention: the po-

sition hx

¯p

, y

¯p

i shows the performance of the given al-

gorithm (A or B) using ¯p on F

and F

. The graphs

in Figure 1 show very different Pareto fronts. While

both reach an equal performance level on both func-

tions, for algorithm A, increasing performance on F

is only possible at the cost of decreasing performance

on F

and vice versa. For B this is not the case, or

at least to a much lesser extent. For B it is possi-

ble to choose a single parameter vector (on the ‘knee’

point) that yields near optimal performance on both

test functions, while for algorithm A this is not pos-

sible. Therefore, one could say that algorithm B is

more robust than algorithm A.

5 EXPERIMENTAL SETUP

As described earlier, the experimental setup consist

of a three layer architecture. On the application layer,

we have chosen two widely used 10 dimensional test-

functions to be solved, namely: Sphere and Rastri-

gin. For the Rastrigin function, the Evolutionary Al-

gorithm is allowed for 8.000 evaluations, and on the

Sphere function 4.000.

On the algorithm layer, we have chosen a simple

genetic algorithm using N-point crossover, bitﬂip mu-

tation, k-tournament parent selection, and determinis-

tic survivor selection. This GA requires 6 parameters

to be deﬁned as described in Table 1. The allowed

values for most of the parameters are deﬁned by ei-

ther the population size or genome length (150). Be-

cause the test-functions require 10 dimensional real-

valued strings as input, a 15-bit Gray coding is used to

transform the binary string of length 150, into a real-

valued string of length 10. For population size, we

have chosen a maximum value of 200, which we be-

lieve is large enough for this genome size and allowed

number of evaluations.

Table 1: Parameters to be tuned, and their ranges.

Parameter Min Max

Population size 2 200

Generation Gap 1 Population Size

Mutation probability 0 1

# crossover points 1 149

Crossover probability 0 1

Tournament size 1 Population Size

On the design layer, M-FETA is used for tuning

the parameters of the Evolutionary Algorithm. The

M-FETA-parameter values used in these experiments

can be found in Table 2.

ICEC 2010 - International Conference on Evolutionary Computation

264

Table 2: M-FETA Parameters.

Population Size 500

Neighborhood Size 30

Signiﬁcance level (α) 0.05

Crossover Probability 1.0

Mutation Probability 0.2

Mutation Size 0.01· (Parameter-Max - Parameter-Min)

Tournament Size 100

Elitism 490

Maximum number of vectors tested 15.000

6 RESULTS

In this section we present and discuss the results of

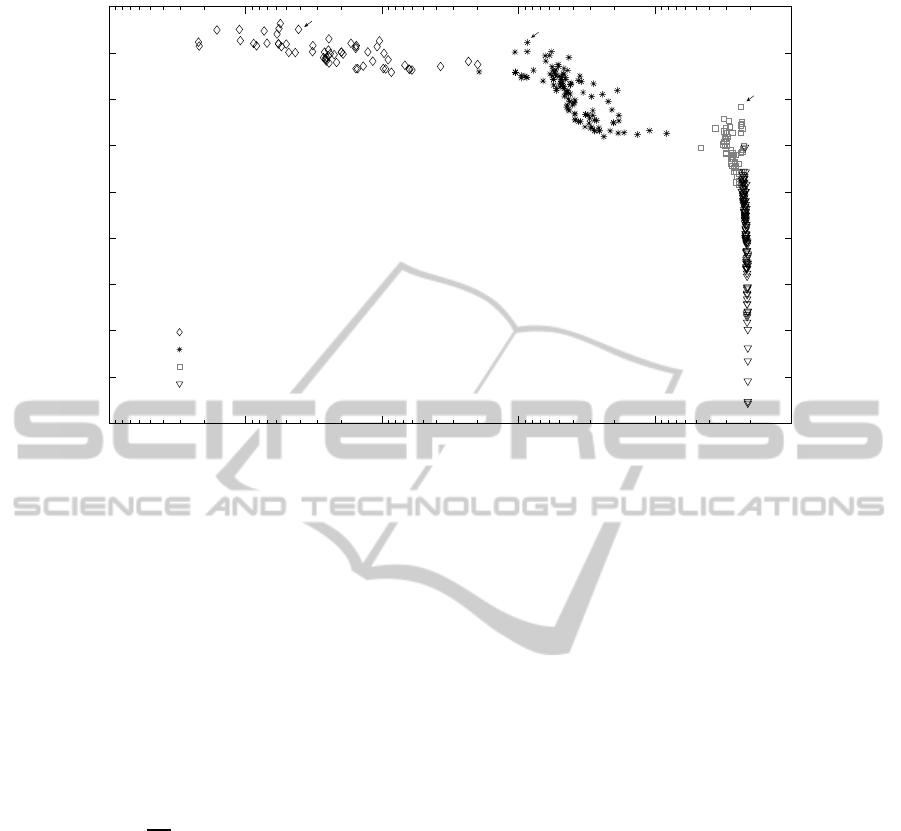
our experiment. Figure 2 shows the Pareto set based

on saved utility valuesof the two used functions as de-

termined by M-FETA (the values have been recorded

when M-FETA was terminated). The utility values

shown in Figure 2 were clustered into four clusters

using the expectation maximization (EM) algorithm

(Dempster et al., 1977) based on their utility values.

Points in the top left and bottom right corners,

clusters D and A, show the specialists, i.e. the pa-

rameter vectors that perform very well on one of the

functions, but much worse on the other. We can ob-

serve, for example, in the bottom right corner (Cluster

A), that, in order to gain even a little on the Sphere

function, one will concede signiﬁcantly on the utility

value of the Rastrigin function. A similar trend can

be observed in the top left corner of Figure 2 (Cluster

D), which shows that to gain on the Rastrigin function

the utility values for the Sphere function will likely to

decrease greatly.

The approximated Pareto front also allows to for a

visual identiﬁcation of a ‘generalist’. However, from

Figure 2 we can see that there is not a single ‘gener-

alist’ parameter vector for the two functions consid-

ered. If there was only a single best generalist, the

shape of the line determined by the points in Figure 2

would resemble a concave line. However, we may

notice that there are two ‘knee-points’ in the line (no-

tice them in Clusters B and C), which indicate two

‘pseudo-generalists’.

In Figure 2, we also show the performance of two

vectors G

that are indicated as ‘generalist’ by

two different single-objective approaches. G

is de-

termined by optimizing on the equally weighted aver-

age performance (MBF) over the two functions used.

However, we can intuitively conclude that G

is not

a true generalist, as it is in the cluster that contains

specialists on the Rastrigin function.

As the ranges of the two optimized functions’ util-

ity values can differ signiﬁcantly, taking the average

of the MBF values can introduce a bias towards one of

the functions. To overcome this problem, a weighted

average of the MBF values is used for optimization.

The weights are determined as follows. By tuning on

the two functions separately, we can record the cor-

responding best parameter vectors and utility values.

These utility values will determine the upper bounds

for the corresponding functions. Then, the best pa-

rameter vector on function F

is used to obtain the

utility on F

, and this utility will serve as the lower

bound for F

. The upper and lower bounds determine

a range for each of our functions, and these ranges are

used as weights in the single-objective function. The

performance of the vector obtained by this method is

shown in Figure 2 as G

In addition to G

and G

in the approximated

Pareto front, by observation, we can identify G

(at

the second knee-point) as well, thus ﬁnding a new

‘pseudo-generalist’. By plotting the Pareto front, we

are also better able to choose ‘where we want to be’,

i.e. it is possible to justify a weight choice by visu-

ally conﬁrming a parameter vector’s usefulness, and

to place a utility value pair in context of other points.

In Section 4 we stated that the parameter Pareto

front can be used to compare the robustness of algo-

rithms as well. Although these experiments are exe-

cuted using only a single algorithm, and our test suite

is quite small, there are some indications we can de-

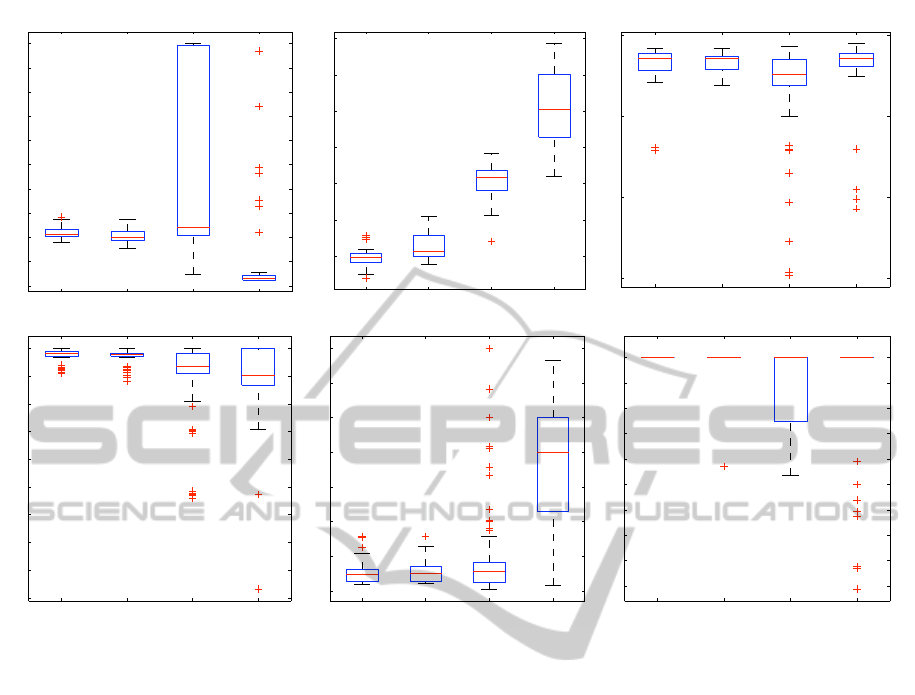
duce for the robustness of the algorithm. Figure 3

shows box plots of parameter vector values corre-

sponding to the clusters identiﬁed above. An indi-

cation of the robustness of the simple GA, can be ob-

tained as follows. For all parameters except the mu-

tation rate, a single parameter value can be found that

is part of all four clusters. This is either because the

values need to be in the same range (such as for tour-

nament size), or because this parameter is not relevant

for reaching a good performance (such as the genera-

tion gap on the Rastrigin function). This indicates that

we can deﬁne a value for these parameters that are op-

timal for both of the functions, except for the mutation

rate, which does not have such a value that works on

AN MOEA-BASED METHOD TO TUNE EA PARAMETERS ON MULTIPLE OBJECTIVE FUNCTIONS

265

!!"

!!%

!!$

!!#

!!!

!!"

+,-./-0123,45246784/249:;,-,4!48

+,-./-0123,45246784/24<1=>-5?524!48

@AB=>,-4C

@AB=>,-4@

@AB=>,-47

@AB=>,-4D

Figure 2: The Parameter Pareto Front of a Simple GA on Sphere and Rastrigin.

both. In the end, we can conclude that the Simple GA

is quite robust, because only the mutation rate needs

to be changed when applied to different preferences

or functions.

With respect to the parameter values themselves,

some interesting conclusions can be drawn. It ap-

pears that the population size always needs to be quite

small, namely around 40. The variation and selec-

tion operators also show unconventional values. The

crossover rate need to be almost equal to 1 as usual,

but the number of crossover points is very high. The

same holds for mutation rate, as the commonly used

convention leads to

150

= 0.0067. To compensate for

these rough variation operators, a very high selection

pressure is applied, as can be seen by the small gen-

eration gap, and an almost deterministic parent selec-

tion.

To summarize, the multi-objective approach al-

lows for identifying specialist, and various ‘pseudo’

or ‘global’ generalists, rather than a single vector.

Furthermore, such an approach gives insight into the

interactions between the performances on the func-

tions of a certain test-suite and can give indications

about the robustness of the tuned algorithm that could

not have been gained using a single-objective ap-

proach.

7 CONCLUSIONS

In this paper we have introduced an algorithm called

M-FETA designed for multi-function tuning. This al-

gorithm is applicable for any number of test-functions

and can cope with noisy measurements of utility,

without requiring a large amount of tests to approx-

imate the parameter Pareto front.

By approximating the parameter Pareto front us-

ing M-FETA, we have been able to investigate inter-

actions between ﬁtness functions, parameter values,

and the evolutionary algorithm. By inspecting the

Pareto front, the trade-off between good performance

on either of the test functions was clearly visible. This

enables EA practitioners to ﬁnd a balanced EA setup

reﬂecting their actual preferences.

We have also been able to identify different ‘gen-

eralists’. The shape of the Pareto front exhibited mul-

tiple knee-points that indicated ‘pseudo-generalists’.

This delivered valuable information, as only one of

them would be discovered by using a simple multi-

function tuning by averaging approach.

Last, but not least, we obtained insights into the

robustness of an EA as well. To be speciﬁc, cluster-

ing the parameter vectors in the Pareto front and ana-

lyzing value distribution for each parameter (the box

plots in Figure 3) we could draw conclusions on the

robustness of the EA parameters.

Although the experiments in this paper are limited

with respect to the number of test-functions, it proofs

the concept that multi-function tuning is not only pos-

ICEC 2010 - International Conference on Evolutionary Computation

266

A B C D

100

120

140

160

180

200

Population size

A B C D

0.01

0.015

0.02

0.025

0.03

0.035

0.04

Mutation rate

A B C D

100

150

Number of crossover points

A B C D

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Crossover rate

A B C D

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Generation gap (norm.)

A B C D

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Tournament size (norm.)

Figure 3: Parameters Value Ranges in each of the clusters.

sible, but also provides unique insights that could not

have been gained by means of single-objective tuning

algorithms. More importantly, it can be used for ac-

quiring ‘generalist’ parameter values that work well

on a given test-suite and also ﬁt the preferences of the

user. In the near future, we will apply M-FETA to

larger test-suites, and more advanced algorithms, to

obtain robust EA’s and gain insights into interactions

between parameters, EA’s and test-functions.

REFERENCES

(2005). Proceedings of the 2005 IEEE Congress on Evolu-

tionary Computation, Edinburgh, UK. IEEE Press.

Bartz-Beielstein, T., Lasarczyk, C., and Preuss, M. (2005).

Sequential parameter optimization. In (CEC, 2005),

pages 773–780 Vol.1.

Bartz-Beielstein, T. and Markon, S. (2004). Tuning search

algorithms for real-world applications: A regression

tree based approach. Technical Report of the Col-

laborative Research Centre 531 Computational Intel-

ligence CI-172/04, University of Dortmund.

Bartz-Beielstein, T., Parsopoulos, K., and Vrahatis, M.

(2004). Analysis of Particle Swarm Optimization Us-

ing Computational Statistics. In Chalkis, editor, Pro-

ceedings of the International Conference of Numerical

Analysis and Applied Mathematics (ICNAAM 2004),

pages 34–37.

Branke, J. (1998). Creating robust solutions by means of

evolutionary algorithms. In PPSN V: Proceedings of

the 5th International Conference on Parallel Problem

Solving from Nature, pages 119–128, London, UK.

Springer-Verlag.

Deb, K. (2001). Multi-Objective Optimization using Evolu-

tionary Algorithms. Wiley-Interscience Series in Sys-

tems and Optimization. John Wiley & Sons, Chich-

ester.

Deb, K. and Gupta, H. (2005). Searching for robust pareto-

optimal solutions in multi-objective optimization. In

EMO, pages 150–164.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm :

Nsga-ii. Evolutionary Computation, IEEE Transac-

tions on, 6(2):182–197.

Dempster, A., Laird, N., and Rubin, D. (1977). Maxi-

mum likelihood from incomplete data via the EM al-

gorithm. Royal Statistical Society B, 39:1–38.

Eiben, A. and Jelasity, M. (2002). A Critical Note on Exper-

imental Research Methodology in EC. In Proceedings

of the 2002 IEEE Congress on Evolutionary Compu-

tation (CEC 2002), pages 582–587. IEEE Press.

AN MOEA-BASED METHOD TO TUNE EA PARAMETERS ON MULTIPLE OBJECTIVE FUNCTIONS

267

Eskandari, H. and Geiger, C. D. (2009). Evolutionary

multiobjective optimization in noisy problem environ-

ments. Journal of Heuristics, 15(6):559–595.

Hughes, E. (2001). Evolutionary multi-objective ranking

with uncertainty and noise. In EMO ’01: Proceed-

ings of the First International Conference on Evolu-

tionary Multi-Criterion Optimization, pages 329–343,

London, UK. Springer-Verlag.

Maron, O. and Moore, A. (1997). The racing algorithm:

Model selection for lazy learners. In Artiﬁcial Intelli-

gence Review, volume 11, pages 193–225.

Nannen, V. and Eiben, A. (2006). A method for parame-

ter calibration and relevance estimation in evolution-

ary algorithms. In Keijzer, M., editor, Proceedings

of the Genetic and Evolutionary Computation Confer-

ence (GECCO-2006), pages 183–190. Morgan Kauf-

mann, San Francisco.

Smit, S. and Eiben, A. (2009). Comparing parameter tuning

methods for evolutionary algorithms. In Proceedings

of the 2009 IEEE Congress on Evolutionary Compu-

tation, pages 399–406, Trondheim. IEEE Press.

Smit, S. and Eiben, A. (2010). Parameter tuning of

evolutionary algorithms: Generalist vs. specialist.

In EvoApplications 2010, Part I, pages 542–551.

Springer.

University, J. F. and Fieldsend, J. E. (2005). Multi-objective

optimisation in the presence of uncertainty. In (CEC,

2005), pages 476–483.

Wolpert, D. H. and Macready, W. G. (1997). No free lunch

theorems for optimization. IEEE Transaction on Evo-

lutionary Computation, 1(1):67–82.

Yuan, B. and Gallagher, M. (2007). Combining Meta-EAs

and Racing for Difﬁcult EA Parameter Tuning Tasks.

In Lobo, F., Lima, C., and Michalewicz, Z., editors,

Parameter Setting in Evolutionary Algorithms, pages

121–142. Springer.

Zitzler, E., Laumanns, M., and Thiele, L. (2001). Spea2:

Improving the strength pareto evolutionary algorithm.

Technical Report 103, Gloriastrasse 35, CH-8092

Zurich, Switzerland.

ICEC 2010 - International Conference on Evolutionary Computation

268