
PARISIAN APPROACH
Reducing Computational Effort to Improve SMT Performance
by setting Resizable Caches
Josefa D´ıaz, Francisco Fern´andez de Vega
University of Extremadura, M´erida, Spain
J. Ignacio Hidalgo, Oscar Garnica
Universidad Complutense de Madrid, Madrid, Spain
Keywords:
Genetic algorithms, Simultaneous multithreading, Optimization, Parisian approach.
Abstract:
Evolutionay Algorithm are techniques widely used in the resolution of complex problems. On the other hand,
Simultaneous Multithreading improves the throughput of the processor core taking advantage of Instruction
Level Parallelism and Thread Level Parallelism. In this environment adaptation the cache configuration, at
runtime according to workloads settings will be improved the processor performance. This improvement is
achieved by using resizable caches. In a previous work, we proposed a Genetic Algorithm to find the better
cache configurations according to the needs and characteristics of the workloads. However the computational
cost needed for the evaluation process is very high. In this paper we propose the use of the Parisian Evolution
Approach to improve dynamically reconfigurable cache designs, and reduce the computational cost associated.
We study the behavior of a set of benchmarks, taking into account their needs over cache memory hierarchy in
each phase of execution, in order to adapt the cache configuration and to increase the number of instructions per
cycle. Experimental results show a large saving in computing time and some improvement on the instructions
per cycle achieved in previous approaches.
1 INTRODUCTION
Simultaneous Multithreading (SMT) (Tullsen et al.,
1996) is a hardware technique which allows multi-
ple threads to issue instructions in the same clock cy-
cle. In an environment where hardware resources are
shared between multiple threads, optimal control of
resources is one of the main objectives to improve the
performance. SMT has the ability to provide hard-
ware resources to a thread, when the current thread
is not using them, due to long latency operations as
memory access, control and data dependencies, etc.,
hiding latencies produced due to these operations.
However, the impact produced by long latency ope-
rations, over some workloads and under certain cir-
cumstances, can lead to threads starvation. One of
the techniques proposed to prevent this problem was
the design of (L´opez et al., 2007) by using a Globally
Asynchronous, Locally Synchronous (GALS) SMT
design, where hardware resources are distributed in
several independent clock domains. These domains
can change its clock frequency and structures sizes
(specifically, cache size) according to the needs of the
running workloads and different phases of the work-
load. Therefore, selecting the appropriate cache sizes
for the running workloads is an important factor that
will allow to increase the thoughput of the system. In
that work, an on-line control algorithm evaluates the
behavior of the cache memory in the previous interval
and changes the cache size for the next interval if it is
needed.
In a preliminary study (D´ıaz et al., 2009), we pro-
posed Evolutionay Algorithms to find how the cache
size should change with time in order to improve
overall performance of the SMT processor. We used
Instructions per Cycle (IPC) as the metric to decide
when to select a new cache size and we do not pre-
dict but do explore the space of possible cache sizes
we are working with. However, exploring all possi-
ble cache sizes, for a workload given, suppose a high
computacional cost and newapproaches are necessary
to reduce it.
275
Díaz J., Fernández de Vega F., Ignacio Hidalgo J. and Garnica O..
PARISIAN APPROACH - Reducing Computational Effort to Improve SMT Performance by setting Resizable Caches.
DOI: 10.5220/0003113702750280
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 275-280
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

In this work, we study Parisian Evolution (PA)
paradigm (Collet et al., 2000) to explore the set of
configurations that optimizes cache memory perfor-
mance for a given workload according to their needs
in each phase of the execution, and improve the pro-
cessor throughput by increasing the IPC. Experimen-
tal results show a small improvement in the IPC ob-
tained, but the main contribution is the reduction of
computation time.
The rest of the paper is organized as follows. Sec-
tion 2 is devoted to present the background of our
work: the adaptive SMT microarchitecture and resi-
zable caches. Section 3 presents the evolutionary al-
gorithm techniques implemented and the simulation
environment used. Section 4 describes our results and
finally in Section 5 we present some conclusions and
future work.
2 SMT MICROARCHITECTURE
2.1 Multiple Clock Domain (MCD) -
GALS Design
As we have mentioned, in this paper we use the
SMT-MCD architecture proposed in (L´opez et al.,
2007). This design has five independent clock do-
mains where each domain can work at a different fre-
quency and is able to adapt the key hardware struc-
tures in order to improve the processor performance.
In this work we focus on the load/store domain and
within it in the Level 1 Data Cache (L1 DCache) and
shared Level 2 Cache (L2 Cache). Only load/store
domain changes its frequency, the rest of domains
work at a fixed frequency. L1 DCache and L2
Cache are implemented using reconfigurable caches
and are changed together with the clock frequency of
load/store domain.
2.2 Resizable Caches
The memory access latency is closely related to its
size: the larger the memory the higher the access
latency and, the smaller the memory the lower the
latency. Moreover the need of a larger capacity or
higher access speed depends on the current workloads
in the system and their execution phase. Achieving a
trade-off between memory size and access speed is a
key factor to improve the throughput of a SMT pro-
cessor.
L1 DCache and L2 Cache placed in the load/store
domain are implemented as dynamically resizable
caches using the Accounting Cache (Dropsho et al.,
2002). The Accounting Cache is a n-way associa-
tive memory divided in two different partitions: the
primary, A, and the secondary, B. The configuration
of the Accounting Cache is defined by the number
of ways assigned to the primary A partition. First,
k ways are assigned to the primary A partition, the re-
mainder n − k ways are assigned to the secondary B
partition. We configure L1 Dcache and L2 Cache as
8-ways associative Accounting Caches and we eva-
luate four configurations in order to reduce the size
of the exploration space. Hence, the configurations
are D0(1/7), D1(2/6), D2(4/4) and D3(8/0) as shown
in Figure 1, and both caches are modified in tandem
with the frequency of the load/store domain.
Figure 1: Ways assigned to partitions A and B, by each
configuration. Yellow, partition A. Green partition B.
The algorithm used in (L´opez et al., 2007) ana-
lyzed the cache misses and hits during the last 15K
instructions in order to decide the cache configuration
for the next interval. In this way they used the cost of
a set of cache references as an indirect indicator of the
processor performance. In a preliminary work (D´ıaz
et al., 2009), we apply GAs to find good configu-
rations for resizable L1 Dcache and L2 Cache of a
SMT processor and we used the IPC as an indicator
the processor performance. However, the higher the
instruction window size of an application, the higher
the computational effort needed.
In this work, we propose to apply the PA Para-
digm (Collet et al., 2000) to explore the better set of
configurationsfor L1 DCache and L2 Cache of a SMT
processor with a higher instruction window size and
we use the IPC as an indicator the goodness of a set
configurations (a problem solution). In the next sec-
tion we explain the methodology used.
ICEC 2010 - International Conference on Evolutionary Computation
276

3 Methodology
3.1 GAs Background
Genetic algorithms (GA) (Holland, 1975) are widely
used to solve search and optimization problems. Se-
veral researchers have already considered the conve-
nience of applying GAs to face problems in the Com-
puter Architecture field. In (D´ıaz et al., 2009), we
used a simple GA whose outline can be seen in Fig-
ure 2 and where each candidate solution was com-
posed by a set of configurations to be applied at spe-
cific intervals when a given benchmarck is running.
The fitness function includes the execution of the
SMT simulator with all customized configurations to
be applied in each interval and returns the result of the
simulation process: IPC. Although, results were not
conclusive, we were optimistic with the methodology
used. However, we need to test with a higher instruc-
! "#
$ %&'
Figure 2: Previous approach used in (D´ıaz et al., 2009). GA
is fed with a set of initial solutions and the returned solution
is an individual with n = 100 genes, each gene describing
the configuration applied in each interval during the simu-
lation of the processor.
tion window size, but the simulation time for each
individual is quite large and the computational cost
grows too. The overall simulation time of a candidate
solution may range from several minutes to several
hours depending on the benchmark. In summary, the
computational cost for a small population size of 30
individuals with 500 ∗ 106 insts. to execute is thus
very high.
In this work, we present the application of PA
Paradigm that could help us to reduce this computa-
tional cost, thus allowing a wider exploration of the
space of posible solutions, in order to find good con-
figurations for L1 DCache and L2 Cache placed in de
load/store domain on a SMT processor. We use this
technique to try to improve the IPC results obtained
with previous approaches. In the next section, we ex-
plain this methodology in more details.
3.2 Parisian Evolution
As it is well known in the Evolutionary Computation
Community, the evaluation process of the candidate
solutions (individuals) is usually the most time con-
suming task of an EA. A good idea is to divide a pos-
sible solution in an appropriate number of subcompo-
nents that depending on the problem can be indepen-
dent or highly dependent on each other.
Classic evolutionary techniques consider an indi-
vidual as a complete solution to solve a given pro-
blem. In contrast PA paradigm (Collet et al., 2000)
defines an individual as a part of solution, similar to
Michigan approach for Classifier Systems (Holland,
1975) which obtained a base rule from a subset of in-
dividual rules evolved. Thus, a complete solution is
obtained by aggregation of multiple individuals. This
approach reduces computational effort at both, indi-
vidual and population levels (Olague et al., 2008).
In order to apply PA we need to meet two key con-
ditions: (i) the problem at hand can be set apart into
separate components by PA; (ii) the local fitness of a
single subcomponent can be calculated. Our problem
satisfies both conditions, as we will see below. There-
fore, the main decisions within PA are:
1. Partial Encoding: number of suitable subcompo-
nents, the individuals aggregation process to cre-
ate a complete solution and the individuals’s con-
tribution.
2. Environment: Designing the environment where
partial solutions interact to achieve better aggre-
gate solutions.
3. Local and Global Fitness: Defining the fitness
function to partial solution.
4. Population Diversity Preservation: Diversity
preservation techniques need to be implemented
in order to promote the diversity.
Therefore, a complete solution (population) is di-
vided into subcomponents of the same size (indivi-
duals). The partial fitness of an individual, will be the
IPC obtained in the interval of execution. The global
fitness is calculated based on the contribution of each
and every one of the individuals. This feature is the
main difference of our approach with the original PA
implementation, since in our problem the different
PARISIAN APPROACH - Reducing Computational Effort to Improve SMT Performance by setting Resizable Caches
277
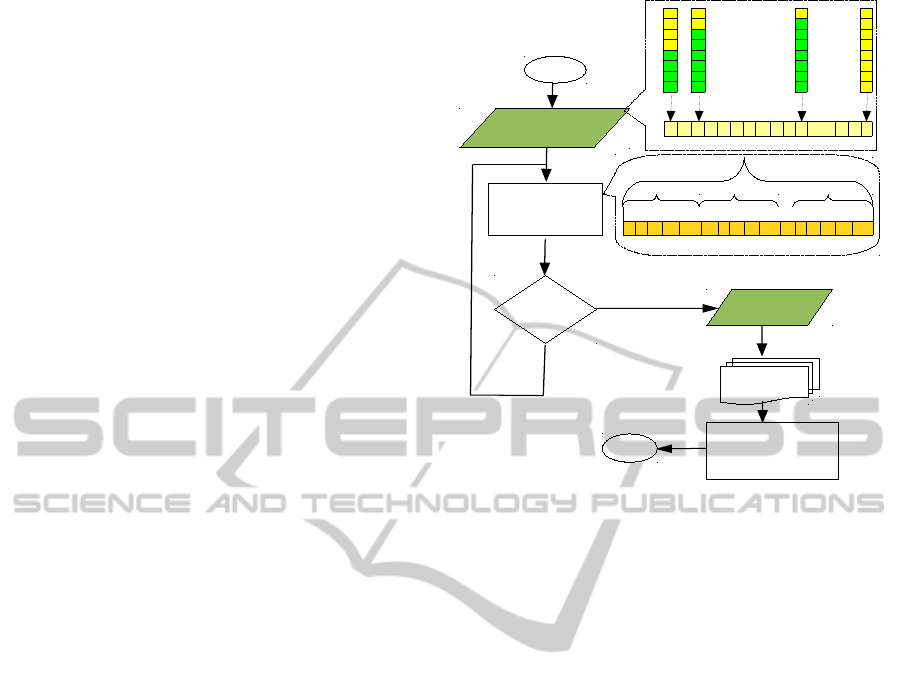
subcomponents are highly dependent on each other
and, one change in an individual affects individuals’
results subsequently evaluated. The execution of a set
of instructions leaves the memory cache in a given
state, this state has a direct influence on the results to
the execution of following instructions. This interde-
pendence is what leads us to propose that all indivi-
duals contribute equally to global fitness of the com-
plete solution. Parameters used in the PA paradigm
are specified below and Figure 3 illustrates the algo-
rithm used in our PA:
• Instruction window size 105∗ 106 instructions.
• Population is a complete solution composed by
a series of configurations between four available
configurations (D0, D1, D2 and D3) and codified
by the alphabet Ω = {0,1,2,3}.
• A configuration is applied every 15K insts. ex-
ecuted and every subcomponents defines an in-
dividual that will execute 1, 5∗ 106 instructions.
The number of genes for an individual is 100 and
we have a population size of 70 individuals.
• The fitness function includes the execution of the
simulator with all customized configurations and
returns the individuals’ IPC, based of them the
IPC of complete solution (global fitness), which
tries to be maximized, it is calculated.
• Tournament selection method is employed with
2 individuals per tournament and standard one-
point random crossover is employed, with a pro-
bability of 0.8.
• A random one point mutation, with a probability
0.01, is applied for changing a specific configura-
tion for a time interval within the chromosome.
3.3 Fitness Function Evaluation
A simulator for SMT architectures is needed to eva-
luate candidate solutions. We use a simulation en-
vironment based on the SimpleScalar toolset with
MCD processor extensions and extended to support a
SMT core (L´opez et al., 2007) and ICOUNT2.8 from
(Tullsen et al., 1996) as fetch policy.
In (D´ıaz et al., 2009) the simulator load the config-
urations from files and applies them sequentially for
intervals of 15K insts. Every simulation finishes when
all the configuration lines have been applied. In this
work, the simulator has been modified to calculate the
fitness value of an individual and return it during the
parisian evolutionary process.
Similarly as in previous work, we have performed
some experiments to evaluate the methodology and in
order to speed up the algorithm we work with two key
!"#$
%
&'()*
+*
,('*
-,
.),
/
0/12
'3/#,45
6.7
Figure 3: Workflow of our approach. PA is fed with a com-
plete solution and the returned solution is other complete
solution composed by a set of individuals where each one
has n = 100 genes, each gene describing the configuration
applied in each interval.
ideas: (1) we run the algorithm on a parallel computer,
so that several individuals or several benchmarks ex-
periments are evaluated simultaneously and (2) we
use a complete solution composed by good configu-
rations obtained in previous methodologies to be in-
jected in the initial population. Therefore the algo-
rithm begin the search with a good value as the start-
ing point for the search process.
3.4 Experiments
In this work, we have performed two experiments
using PA, where we use all individuals with their lo-
cal fitness to calculate global fitness: (i) Normal evo-
lution (PA-1) with selection, crossover and mutation
operations and (ii) creating a new generation based
on the lastest generation and modifying some indivi-
duals by a “local search” between using the best indi-
viduals until that generation (PA-2). This second ap-
proach arises because we keep the ten best complete
solutions (the global fitnes and the local fitness of all
individuals). Therefore, a good solution could come
from those solutions that have been considered as the
best solutions. So every 15 generations, we create a
new generation of individuals, originally composed
of the previous generation and change 20% of indivi-
duals that are replaced by the best individual, between
ICEC 2010 - International Conference on Evolutionary Computation
278

those which occupy the same position in the ten best
solutions saved until that time. The new generation is
evaluated and if the global fitness is better than pre-
vious generation, we continue with it, otherwise we
recover the previous generation.
4 EXPERIMENTAL RESULTS
In this work, we use master/worker as parallel pro-
gramming paradigm, and our approach has been im-
plemented following this model. Hence, all the ex-
periments were run on a cluster with 22 nodes, with
the main process (running on the front-end processor)
in charge of the whole PA algorithm –keeps the po-
pulation, performs selection, crossover and mutation
operations–, and worker processes (running in worker
processors) are in charge of computing fitness func-
tions (by far the most computing intensive task). In
this approach, each benchmark simulated only need a
worker processor to evaluate all individuals (a com-
plete solution), therefore all bechmarks are simulated
simultaneously using a master/worker model. In this
work, our workload is composed of twelve programs
from the SPEC2000 suite.
In the cases we have seen in section 3.4 we left to
run the algorithm during 150 generations and we clas-
sify the results based on two points of view: (i) Qual-
ity and (ii) Performance. We show results obtained in
the next subsections and we compared it with those
obtained in (L´opez et al., 2007).
4.1 Quality Results
We firstly analyzed quality of result where the objec-
tive is to maximize the IPC, comparing the IPC ob-
tained in (L´opez et al., 2007) with our results: Ta-
ble 1 compared results obtained for integer bechmarks
and Table 2 shows results obtained for floating point
benchmarks with both approaches.
Table 1: Comparison integer benchmarks IPC in both two
PA versus (L´opez et al., 2007b).
Benchmark Prev. Approach PA(1) PA(2)
gzip 2.0480 2.0713 2.0693
vpr 1.8621 1.9475 1.9448
cc1 1.2273 1.2314 1.2286
mcf 3.5278 3.5319 3.5302
crafty 2.0196 2.0218 2.0176
twolf 3.8961 3.8993 3.8958
These results were obtained after running 3 exe-
cutions during 150 generations and the improvement
Table 2: Comparison Floating-Point Benchmarks in both
two PA approach implemented versus [L´opez et al., 2007b].
Benchmark Prev. Approach PA (1) PA(2)
swim 3.4854 3.4855 3.4855
applu 1.8941 1.9240 1.9238
galgel 3.7409 3.7510 3.7480
art 0.8634 0.9024 0.9073
hline equake 3.4105 3.4130 3.4101
lucas 3.1293 3.1293 3.1294
achieved are not conclusive. The overall average im-
provement to the first approach is 0,8237% and for
the second is 0,7229%. The most important improve-
ment is seen in vpr with 4,5862% for the first approx-
imation and 4,4412% for the second, and gzip with
1,1377% and 1,0400% respectively. The rest of bech-
marks did not improve or the improvement achieved
is not relevant.
Table 2 shows the results of floating-point bench-
marks for both implementations compared with pre-
vious approach in (L´opez et al., 2007). For the
same number of execution (3) and during 150 gen-
erations, the improvement achieved is not conclu-
sive and their behaviors are similar to integer bench-
marks. The overall average improvement is 0,4938%
and 0,4872% and only applu and art achieve the most
important improvement with 1,5786% - 1,5680% and
4,5170% - 5,0845% for each approach implemented
respectively. As integer benchmarks, the rest did not
achieve a conclusive improvement or this improve-
ment is not relevant.
However, the second approach obtains worse per-
formance than the first, in most of the benchmarks.
Vpr is the only one that improves over the previous
approach. In our PA implementation we are actually
using only one global individual. It is possible that
the Local Search process stops the normal evolution
of the algorithm, since when a local search solution
is generated we could be climbing to a far point of
the search space. Hence, we should improve in future
works the generation of local search solutions by (i)
assuring that we are studying real neighbor solutions
and (ii) increasing the number of global solutions.
4.2 Performance Results
In this subsection performance’s results are shown.
We must bear in mind that the only difference with
the previous approach (D´ıaz et al., 2009) is the PA
paradigm employed. Both the master/worker ap-
proach and the blade system were also used before
in the same conditions. We can see how the reduction
of time is very important using PA paradigm and the
IPC obtained with this approach is similar or greater
PARISIAN APPROACH - Reducing Computational Effort to Improve SMT Performance by setting Resizable Caches
279
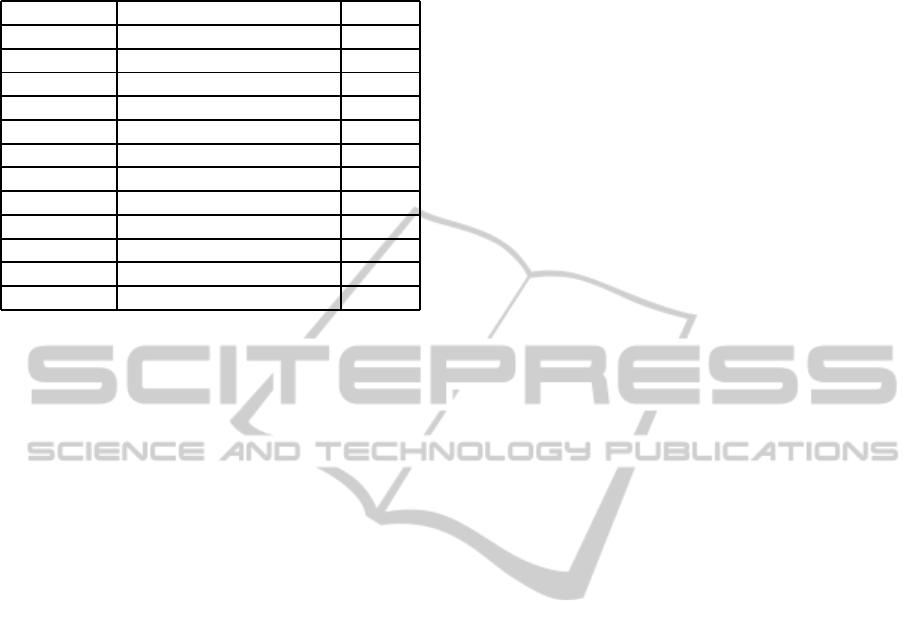
Table 3: Comparison computacional effort (in hours) with
PA paradigm and the previous approach (GA).
Benchmark Previous Approach (GA) PA
gzip 4025,00 115.75
vpr 7875,00 115.61
cc1 3500,00 140.35
mcf 3675,00 94,42
crafty 1225,00 110.25
twolf 2975,00 94.19
swim 2450,00 98.08
applu 5250,00 131.59
galgel 3500,00 109.84
art 10150,00 196.68
equake 3675,00 93.25
lucas 5600,00 115.26
than whose obtained with previous approaches.
The time specified to the previous approach with
GA is an estimation based on the evaluation time of a
complete solution as individual and if we had to eva-
luate a population size of 70 individuals for 150 gen-
erations
5 CONCLUSIONS
In this paper, the Parisian Evolution paradigm has
been used to improve the performance of a SMT pro-
cessor by selecting the optimal configuration of re-
sizable cache memories, while reducing associated
computational cost. In previous works, Resizable
cache memories have demonstrated their efficiency to
improve processor performance by adapting, at run-
time, their configurations according to workload re-
quirements. Some authors have used an indirect ap-
proach to both estimate processor performance at run
time and select the best cache configuration. In a pre-
vious work, we use GA with a small instruction win-
dow size, to select the set of cache configurations that
optimizes processor performance for a given work-
load, however when we increase the instruction win-
dow size the computational effort necesary is very
high.
Parisian Evolution paradigm allow us to work
with greater instruction window size by dividing a
complete solution into subcomponents of the same
size, each one of them is an individual with a local
fitness. Through the cooperative collaboration bet-
ween them gives the global fitness value associated
with the complete solution. However, the improve-
ment obtained is not conclusive, since a few bench-
marks improveand this improvement is small, perfor-
mance’s results obtained allow us to be veyoptimistic.
We think this way can lead us to obtain good results
by searching techniques that allow us to optimize the
workloads’ performance. As future work we will im-
provelocal search techniques and do new experiments
to complete the study. We cannot forget, the final goal
is to find a set of rules that dynamically determines the
best cache configuration for a workload features.
ACKNOWLEDGEMENTS
This work has been partially supported by projects:
CICYT TIN 2008-00508, MEC Consolider Ingenio
2010 2007/2011; Spanish Ministry of Education and
Science under Project TIN2008-06681-C06-01 and
regional government Junta de Extremadura under
projects PDT-08A09, GRU-09105 and FEDER
REFERENCES
Collet, P., Lutton, E., Raynal, F., and Schoenauer, M.
(2000). Polar ifs + parisian genetic programming = ef-
ficient ifs inverse problem solving. Genetic Program-
ming and Evolvable Machines, pages 339–361.
D´ıaz, J., Hidalgo, J. I., Fern´andez, F., Garnica, O., and
L´opez, S. (2009). Improving smt performance: an ap-
plication of genetic algorithms to configure resizable
caches. Proc. of the 11th Annual Conf. Companion on
Genetic and Evolutionary Computation Conf.: Late
Breaking Papers, pages 2029–2034.
Dropsho, S., Buyuktosunoglu, A., Balasubramonian, R.,
Albonesi, D., Dwarkadas, S., Semeraro, G., Magklis,
G., and Scott, M. (2002). Integrating adaptive on-chip
storage structures for reduced dynamic power. In In
proc. 11th Int’l. Conf. on Parallel Architectures and
Compilation techniques, pages 141–152.
Holland, J. (1975). Adaptation in Natural and Artificial Sys-
tems. University of Michigan Press.
L´opez, S., Dropsho, S., Albonesi, D., Garnica, O., and Lan-
chares, J. (2007). Rate-driven control of resizable
caches for highly threaded smt processors. In 16th
Int’l. Conf. on Parallel Architecture and Compilation
Techniques(PACT 2007), page 416.
Olague, G., Dunn, E., and Lutton, E. (2008). Individual
Evolution as an Adaptive Strategy for Photogrammet-
ric Network Design.
Tullsen, D. M., Eggers, S. J., Levy, H. M., Emer, J. S., Lo,
J. L., and Stamm, R. L. (1996). Exploiting choice: In-
struction fetch and issue on an implementable simul-
taneous multithreading processor. In Proc. 23rd Int’l
Sump. on Computer Architecture, pages 191–202.
ICEC 2010 - International Conference on Evolutionary Computation
280
