SIMPLE GENETIC ALGORITHM WITH α-SELECTION

Intrinsic System Model, Fixed Points and the Fixed Point Graph

Andr´e Neubauer

Information Processing Systems Lab, M¨unster University of Applied Sciences

Stegerwaldstraße 39, D-48565 Steinfurt, Germany

Keywords:

Simple genetic algorithm, α-selection, Random heuristic search, Dynamical system model, Inﬁnite population

model, Fixed point graph.

Abstract:

Genetic algorithms (GA) are instances of random heuristic search (RHS) which mimic biological evolution

and molecular genetics in simpliﬁed form. These random search algorithms can be theoretically described

with the help of a deterministic dynamical system model by which the stochastic trajectory of a population

can be characterized using a deterministic heuristic function and its ﬁxed points. For practical problem sizes

the determination of the ﬁxed points is unfeasible even for the simple genetic algorithm (SGA). The recently

introduced simple genetic algorithm with α-selection allows the analytical calculation of the unique ﬁxed

points of the dynamical system model. In this paper, an overview of the theoretical results for the simple ge-

netic algorithm with α-selection and its corresponding intrinsic system model is given. Further, the connection

to the ﬁxed point graph is illustrated which describes the asymptotic behavior of the simple genetic algorithm.

In addition to the theoretical analysis experimental results for the simple genetic algorithm with α-selection,

uniform crossover and bitwise mutation are presented.

1 INTRODUCTION

As speciﬁc instances of random heuristic search

(RHS), genetic algorithms mimic biological evolu-

tion and molecular genetics in simpliﬁed form (Vose,

1999b). Genetic algorithms (GA) process popula-

tions of individuals which evolve according to selec-

tion and genetic operators like crossover and muta-

tion (Holland, 1992). The algorithm’s stochastic dy-

namics can be described with the help of a dynamical

system model introduced by VOSE et al. (Reeves and

Rowe, 2003; Vose, 1999b; Vose, 1999a). The pop-

ulation trajectory is attracted by the ﬁxed points of

an underlying deterministic heuristic function which

also yields the expected next population. However,

even for moderate problem sizes the calculation of the

ﬁxed points is difﬁcult.

The simple genetic algorithm (SGA) with α-

selection recently introduced in (Neubauer, 2009;

Neubauer, 2008a; Neubauer, 2008c; Neubauer,

2008b) allows to explicitly derive the ﬁxed points of

the heuristic function. In this selection scheme, the

best or α-individual is mated with individuals ran-

domly chosen from the current population with uni-

form probability. For the simple genetic algorithm

with α-selection it is further possible to formulate an

intrinsic system model which is compatible with the

equivalence relation imposed by schemata. The in-

trinsic system model provides a means to analyze the

genetic algorithm’s exploitation and exploration of

the search space due to the mixing operation caused

by crossover and mutation irrespective of the ﬁtness

function.

This paper gives an overview of the theoretical re-

sults for the simple genetic algorithm with α-selection

and its intrinsic system model. It further outlines the

connection to the ﬁxed point graph which describes

the asymptotic behavior of the simple genetic algo-

rithm. In addition to the theoretical analysis experi-

mental results are presented. The paper is organized

as follows. The simple genetic algorithm with α-

selection is described as a speciﬁc instance of random

heuristic search in Sect. 2 based on the notion of the

best individual randomly mating with other individ-

uals in the current population. In Sect. 3 the corre-

sponding dynamical system model is derived based

on which the intrinsic system model of the simple ge-

netic algorithm with α-selection is formulated in Sect.

4. Simulation results for the simple genetic algorithm

with α-selection, uniform crossover and bitwise mu-

281

Neubauer A..

SIMPLE GENETIC ALGORITHM WITH a-SELECTION - Intrinsic System Model, Fixed Points and the Fixed Point Graph.

DOI: 10.5220/0003113802810288

In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 281-288

ISBN: 978-989-8425-31-7

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

tation are presented showing a close agreement be-

tween theory and experiment. The ﬁxed point graph

of the simple genetic algorithm with α-selection is il-

lustrated in Sect. 5. A brief conclusion and an outline

of future research is given in Sect. 6.

2 SIMPLE GENETIC

ALGORITHM WITH

α-SELECTION

In this section, the simple genetic algorithm with α-

selection, uniform crossover and bitwise mutation is

described following the notation and deﬁnition of the

simple genetic algorithm (SGA) in (Vose, 1999b). It

is assumed that the genetic algorithm is used for the

maximization of a ﬁtness function f : Ω → R which is

deﬁned over the search space Ω = Z

ℓ

= {0, 1}

ℓ

con-

sisting of binary ℓ-tuples (a

,.. .,a

ℓ−1

Each binary ℓ-tuple (a

,..., a

ℓ−1

) =

...a

ℓ−1

will be identiﬁed with the integer

a = a

· 2

ℓ−1

+ a

· 2

ℓ−2

+ . .. + a

ℓ−1

· 2

leading

to the search space Ω = {0,1, ...,n − 1} with

cardinality |Ω| = n = 2

ℓ

. The ﬁtness values are

given by f(a) = f

. Based on the binary number

representation the bitwise modulo-2 addition a ⊕ b,

bitwise modulo-2 multiplication a ⊗ b and bitwise

binary complement a are deﬁned. Vice versa,

the integer a ∈ Ω is viewed as a column vector

,... ,a

ℓ−1

)

. The all-one ℓ-tuple 1 corresponds

to the integer n − 1 = 2

ℓ

− 1. The indicator function

is deﬁned by [i = j] = 1 if i = j and 0 if i 6= j.

2.1 Algorithm

The simple genetic algorithm with α-selection works

over populations P(t) deﬁned as multisets of r indi-

vidual binary ℓ-tuples a(t) ∈ Ω. For the creation of

offspring individuals in each generation t genetic op-

erators like crossover χ

Ω

and mutation µ

Ω

are applied

to parental individuals (see Fig. 1).

2.2 α-Selection

For the α-selection scheme let

b(t) = argmax{ f

: i ∈ P(t)} (1)

be the best individual or α-individual in the current

population P(t). In the simple genetic algorithm with

α-selection the α-individual b(t) is mated with indi-

viduals randomly chosen from the current population

P(t) with uniform probability r

−1

t := 0;

initialize population P(0);

while end of adaptation 6= true do

select α-individual b(t) as ﬁrst parent;

for the creation of r offspring do

select second parent c(t) randomly;

apply crossover χ

Ω

and mutation µ

Ω

a(t + 1) := µ

Ω

(χ

Ω

(b(t), c(t)));

end

increment t := t + 1;

end

Figure 1: Simple genetic algorithm with α-selection

(Neubauer, 2009; Neubauer, 2008a; Neubauer, 2008c;

Neubauer, 2008b).

2.3 Mixing

The crossover operator χ

Ω

: Ω × Ω → Ω randomly

generates an offspring ℓ-tuple a = (a

,... ,a

ℓ−1

)

according to a = χ

Ω

(b,c) with crossover probabil-

ity χ from two ℓ-tuples b = (b

,... ,b

ℓ−1

) and

c = (c

,... ,c

ℓ−1

). With the crossover mask m ∈ Ω

the ℓ-tuples

a = b⊗ m⊕ m⊗ c (2)

a = b⊗ m⊕ m⊗ c (3)

are generated one of which is chosen as offspring a

with equal probability 2

−1

. For uniform crossover

the crossover mask m is randomly chosen from Ω

according to the probability distribution vector χ =

(χ

,χ

,... ,χ

n−1

)

with (Vose, 1999b)



1− χ+ χ · 2

−ℓ

, m = 0

χ· 2

−ℓ

, m > 0

. (4)

The bitwise mutation operator µ

Ω

: Ω → Ω,

which randomly ﬂips each bit of the ℓ-tuple a =

,... ,a

ℓ−1

) with mutation probability µ, is de-

ﬁned with the help of the mutation mask m ∈ Ω ac-

cording to µ

Ω

(a) = a ⊕ m. The mutation mask m is

randomly chosen from Ω according to the probability

distribution vector µ = (µ

,µ

,... ,µ

n−1

)

with (Vose,

1999b)

= µ

· (1− µ)

ℓ−1

. (5)

A typical value of the mutation probability is µ ∼

ℓ

3 DYNAMICAL SYSTEM MODEL

In the dynamical system model (Vose, 1999b) the

dynamics of the simple genetic algorithm is com-

pactly formulated by deﬁning the population vector

ICEC 2010 - International Conference on Evolutionary Computation

282

p = (p

, p

,... , p

n−1

)

. Each component

∑

j∈P

[ j = i] (6)

gives the proportion of the element i∈ Ω in the current

population P. The population vector p is an element

of the simplex

Λ =

(

p ∈ R

: p

≥ 0∧

∑

i∈Ω

= 1

)

. (7)

For a population of size r the number of possible pop-

ulation vectors is given by



n+r−1



. In the limit of in-

ﬁnite populations with r → ∞ the population vectors

are dense in the simplex Λ. For simplicity we will take

the simplex Λ as the deﬁning region of the population

vector p which is strictly valid only for large popula-

tions with r ≫ 1 in the sense of an inﬁnite population

model.

The simple genetic algorithm is now described as

an instance of RHS τ : Λ → Λ according to p(t + 1) =

τ(p(t)) with τ depending on the random selection and

genetic operators. As outlined in (Vose, 1999b) τ

can be equivalently represented by a suitable heuristic

function G : Λ → Λ which for a given population vec-

tor p yields the probability distribution G (p). This

probability distribution

G (p)

= Pr{individual i is sampled from Ω} (8)

is used to generate the next population p(t+1) in gen-

eration t + 1 from the population p(t) in generation t

as illustrated in Fig. 2. The transition probabilities of

the RHS τ are given by the formula (Vose, 1999b)

Pr{τ(p) = q} = r!

∏

i∈Ω

G (p)

(rq

. (9)

p(t)

p(t + 1)

G (p(t))

sample in Ω

Figure 2: Simple genetic algorithm as RHS τ with heuristic

function G .

The trajectory p, τ(p), τ

(p), ... approximately

follows the trajectory p, G (p), G

(p), ... of the de-

terministic dynamical system deﬁned by the heuristic

function G with

E{τ(p)} = G (p) . (10)

Because of the corresponding mean quadratic devia-

tion

E{kτ(p) − G (p)k

} =



1− kG (p)k



(11)

the RHS τ behaves like the deterministic dynamical

system model in the limit of inﬁnite populations with

r → ∞. As illustrated by experimental evidence the

RHS τ shows punctuated equilibria, i.e. phases of rel-

ative stability nearby a ﬁxed point ω = G (ω) of the

heuristic function G disrupted by sudden transitions

to another dynamical equilibrium near another ﬁxed

point. We call this the ﬁxed point hypothesis of ge-

netic algorithms.

3.1 Heuristic

In the simple genetic algorithm with α-selection the

α-individual

b = argmax{ f

: i ∈ Ω∧ p

> 0} (12)

is selected as the ﬁrst parent for creation of a new off-

spring, whereas the second parent is chosen uniformly

at random from the current population according to

the probability distribution p

over Ω with j ∈ Ω. The

heuristic function G (p) follows to

G (p)

∑

j∈Ω

· Pr{µ

Ω

(χ

Ω

(b, j)) = i} . (13)

The probability distributions for crossover χ

Ω

and

mutation µ

Ω

lead to

Pr{µ

Ω

(χ

Ω

(b, j)) = i} = (14)

∑

u,v∈Ω

+ χ

· [b⊗ u⊕ u⊗ j = i⊕ v] .

By deﬁning the n× n mixing matrix (Vose, 1999b)

i, j

∑

u,v∈Ω

+ χ

· [i⊗ u⊕ u⊗ j = v] (15)

this yields Pr{µ

Ω

(χ

Ω

(b, j)) = i} = M

i⊕b,i⊕ j

and ﬁ-

nally

G (p)

∑

j∈Ω

· M

i⊕b,i⊕ j

. (16)

With the permutation matrix (σ

)

i, j

= [i⊕ j = b] and

the twist (M

∗

)

i, j

= M

i⊕ j,i

of the symmetric mixing

matrix M = M

the new population vector is given

q = G (p) = σ

· M

∗

· σ

· p . (17)

This dynamical system model is illustrated in Fig. 3.

SIMPLE GENETIC ALGORITHM WITH a-SELECTION - Intrinsic System Model, Fixed Points and the Fixed Point

Graph

283

∗

Figure 3: Dynamical system model of the simple genetic

algorithm with α-selection (Neubauer, 2008a).

3.2 Mixing Matrix

The calculation of the mixing matrix M can be carried

out efﬁciently with the help of the WALSH transform

(Vose and Wright, 1998). For a matrix M the WALSH

transform is

M = W · M · W with the n × n WALSH

matrix W

i, j

= n

−1/2

· (−1)

. The WALSH matrix W

is symmetric and orthogonal, i.e. W

−1

= W

= W.

The WALSH transform of a vector v yields

v = W · v.

In Fig. 4 the WALSH matrix W is illustrated for n =

= 64.

Figure 4: Illustration of the WALSH matrix W for n = 2

64.

For crossover and bitwise mutation the WALSH

transform of the mixing matrix M is given by (Vose,

1999b)

i, j

= [i⊗ j = 0]· (18)

(1− 2µ)

(i⊕ j)

∑

k∈Ω

i⊗ j



k⊕i

+ χ

k⊕ j



with

Ω

= {i ∈ Ω : i⊗ k = 0} . (19)

Due to the factor [i⊗ j = 0] the components

i, j

are

nonzero only if i⊗ j = 0 or j ∈ Ω

, respectively. The

WALSH transform of the twist of the mixing matrix

can be calculated from



∗∧



i, j

i⊕ j, j

. (20)

4 INTRINSIC SYSTEM MODEL

The matrix σ

·M

∗

·σ

of the dynamical system model

of the simple genetic algorithm with α-selection in

Eq. (17) depends on the mixing matrix M and the

α-individual b. Because of σ

−1

= σ

this yields the

equivalent formulation

q = M

∗

· σ

p . (21)

The permuted population vector σ

p develops ac-

cording to the matrix M

∗

which is independent of

the α-individual b. The matrix M

∗

deﬁnes the in-

trinsic system model of the genetic algorithm with α-

selection (Neubauer, 2008a).

4.1 Fixed Point

The ﬁxed points of the intrinsic system model are

obtained from the eigenvectors of M

∗

to eigenvalue

λ = 1, i.e.

ω = M

∗

· ω . (22)

The ﬁxed points of the heuristic function G of the dy-

namical system model follow from the permutation

ω for a given α-individual b. For the ﬁxed point

analysis of the dynamical system model it therefore

sufﬁces to analyze the intrinsic system model shown

in Fig. 5.

∗

Figure 5: Intrinsic system model of the genetic algorithm

with α-selection (Neubauer, 2008a).

To this end, the WALSH transform of both sides of

the equation q = M

∗

· p is taken yielding

q = W · q = W · M

∗

·W ·W · p = M

∗∧

p . (23)

For an eigenvector v with eigenvalue λ it follows

∗

· v = λ · v and equivalently M

∗∧

v = λ ·

v, i.e. the

matrix M

∗

and its WALSH transform M

∗∧

have the

same eigenvalues with eigenvectors which are also re-

lated by the WALSH transform.

For crossover and mutation the WALSH transform

of the mixing matrix fulﬁlls

i, j

∝ [i⊗ j = 0], i.e.

M is

separative. M

∗∧

= M

∧∗∗

is a lower triangular matrix

the spectrum of which is given by the ﬁrst column of

M (Vose, 1999b). Since the spectrum of M

∗

and its

WALSH transform M

∗∧

are the same this yields the

eigenvalues



∗∧



i,i

0,i

. (24)

ICEC 2010 - International Conference on Evolutionary Computation

284

For crossover and bitwise mutation the eigenvalues

are given by

(1− 2µ)

∑

k∈Ω

(χ

+ χ

k⊕i

) . (25)

Because of λ

= 1 and

0 ≤ λ

≤

− µ <

(26)

for 1 ≤ i ≤ n − 1 there exists a single eigenvector ω

which is a unique ﬁxed point of the intrinsic system

model. For uniform crossover the eigenvalues are ob-

tained from

= (1− 2µ)



χ· 2

−1

1− χ



(27)

for 1 ≤ i ≤ n − 1. The ﬁxed points of the heuristic

function G of the simple genetic algorithm with α-

selection are obtained from the permutation σ

ω for a

given α-individual b. According to the ﬁxed point hy-

pothesis the population will stay near this ﬁxed point

ω and converge to a new ﬁxed point if a better α-

individual is found.

The unique ﬁxed point ω of the intrinsic system

model can be determined explicitly with the help of

the WALSH transform. Due to the relation

ω = M

∗∧

ω and the lower triangular matrix M

∗∧

the WALSH

transform of the ﬁxed point can be recursively calcu-

lated according to

1−

0,i

i−1

∑

j=0

i⊕ j, j

(28)

for 1 ≤ i ≤ n− 1 starting with

= n

−1/2

(29)

which ensures

∑

i∈Ω

= 1. The unique ﬁxed point

ω is then obtained via the inverse WALSH transform

ω = W ·

ω.

The transition in one generation t from popula-

tion vector p(t) to population vector p(t + 1) of the

random heuristic search τ in Fig. 2 can be detailed

for the simple genetic algorithm with α-selection as

shown in Fig. 6. Under the assumption of the ﬁxed

point hypothesis for the intrinsic system model the

permuted population vector σ

b(t)

p(t) will stay near

the unique ﬁxed point ω. The population in gener-

ation t + 1 is therefore approximately sampled from

the search space Ω according to the probability dis-

tribution σ

b(t)

ω with time-independent ﬁxed point ω

and α-individual b(t) as illustrated in Fig. 7.

p(t)

p(t + 1)

b(t)

∗

b(t)

p(t)

b(t)

∗

sample in Ω

Figure 6: Simple genetic algorithm with α-selection as RHS

τ with intrinsic system model M

∗

p(t) p(t + 1)

b(t)

sample in Ω

Figure 7: Simple genetic algorithm with α-selection as RHS

τ with unique ﬁxed point ω.

4.2 Convergence

The matrix M

∗

deﬁning the intrinsic system model of

the simple genetic algorithm with α-selection has the

real eigenvalues λ

= 1 and 0 ≤ λ

≤

− µ <

for

1 ≤ i ≤ n− 1. The corresponding JORDAN canonical

form of M

∗

is given by

J = S

−1

∗

S . (30)

This matrix J consists of simple JORDAN sub-

matrices J

(λ

) along the main diagonal and zeros

elsewhere, i.e.

J = diag



(λ

),J

(λ

),...,J

κ−1

(λ

κ−1

)



(31)

with the κ distinct eigenvalues λ

each of algebraic

multiplicity ν

. The n columns s

of the JORDAN

canonical form J form a basis, i.e. the permuted pop-

ulation vector can be formulated as follows

b(t)

p(t) =

n−1

∑

j=0

(t) · s

. (32)

SIMPLE GENETIC ALGORITHM WITH a-SELECTION - Intrinsic System Model, Fixed Points and the Fixed Point

Graph

285

The trajectory of the permutated population vec-

tor σ

b(t)

p(t) can be obtained from the intrinsic sys-

tem model of the genetic algorithm with α-selection

according to

b(t)

p(t) = (M

∗

)

· σ

b(0)

p(0) . (33)

Using the expansion of this vector in the basis formed

by the columns of the JORDAN canonical form J this

leads to (Vose, 1999b)

b(t)

p(t) = (34)

κ−1

∑

i=0

i+1

−1

∑

j=υ

min{t, j−υ

}

∑

k=0





· λ

t−k

· c

j−k

(0)

with

i−1

∑

j=0

. (35)

The convergence of the permuted population vec-

tor σ

b(t)

p(t) to the unique stable ﬁxed point ω of the

intrinsic system model of the simple genetic algo-

rithm with α-selection is determined by the eigenval-

ues λ

. Because of the single eigenvalue λ

= 1 with

algebraic multiplicity ν

= 1 and therefore υ

= 0,

= 1 it follows

b(t)

p(t) = s

· c

(0)+ (36)

κ−1

∑

i=1

i+1

−1

∑

j=υ

min{t, j−υ

}

∑

k=0





· λ

t−k

· c

j−k

(0)

for t ≥ 1. With the remaining eigenvalues λ

for

1 ≤ i ≤ n− 1 the convergence properties of the sim-

ple genetic algorithm with α-selection can be charac-

terized by introducing the time constants τ

according

= e

−t/τ

(37)

leading to

= −

ln(λ

)

≤

1+ 2µ

< 2 (38)

by taking into account 0 ≤ λ

≤

−µ <

. Due to this

upper bound on the time constants τ

for 1 ≤ i ≤ n− 1

the permuted population vector σ

b(t)

p(t) rapidly con-

verges to the unique stable ﬁxed point ω of the intrin-

sic system model of the simple genetic algorithm with

α-selection.

4.3 Experimental Results

In this section, the ONEMAX problem with ﬁtness

function

= 1

i (39)

is considered, i.e. f

denotes the number of 1’s in the

binary representation of i ∈ Ω. A simple genetic algo-

rithm with α-selection using uniform crossover, bit-

wise mutation and random initial population is used

with the strategy parameters ℓ = 10, n = 2

ℓ

= 1024,

χ = 0.75, µ = ℓ

−1

and r = 100. The unique ﬁxed point

ω of the intrinsic system model is shown in Fig. 8.

0 100 200 300 400 500 600 700 800 900 1000

0.05

0.1

0.15

0.2

0.25

Figure 8: Fixed point of the intrinsic system model of the

simple genetic algorithm with α-selection.

The EUCLIDean distance of the simulated and per-

muted population vector σ

b(t)

p(t) in generation t to

the ﬁxed point ω is given by



b(t)

p(t) − ω



∑

i∈Ω





b(t)

p(t)



− ω



(40)

In Fig. 9 this EUCLIDean distance is shown for one

simulation run. The permuted population vector

b(t)

p(t) rapidly converges to the unique ﬁxed point

ω of the intrinsic system model of the simple ge-

netic algorithm with α-selection and stays close to

this ﬁxed point.

5 FIXED POINT GRAPH

The stable ﬁxed points of the simple genetic algorithm

with α-selection are given by

= σ

ω (41)

with the unique ﬁxed point ω of the intrinsic system

model and b ∈ Ω. As shown in Sect. 4.3 the trajectory

of the simple genetic algorithm with α-selection stays

near the ﬁxed points σ

ω according to the ﬁxed point

hypothesis.

We will now formulate the connection of the dy-

namical system model and its ﬁxed points to the ﬁxed

ICEC 2010 - International Conference on Evolutionary Computation

286

0 10 20 30 40 50 60 70 80 90 100

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

kσ

b(t)

p(t) − ωk

Figure 9: EUCLIDean distance kσ

b(t)

p(t) − ωk over gener-

ation t for the simple genetic algorithm with α-selection.

point graph which describes the asymptotic behavior

of the simple genetic algorithm (Vose, 1999b). Due

to the nature of this paper as a position paper, the fol-

lowing is more speculative than the preceding results.

To this end, let F be the set of ﬁxed points ω

= σ

with b ∈ Ω, i.e.

F = {ω

,ω

,..., ω

n−1

} (42)

= {σ

ω,σ

ω,... ,σ

n−1

ω} .

According to (Vose, 1996; Vose, 1999b) the RHS

τ can be modeled by a meta level MARKOV chain C

over the ﬁxed points ω

= σ

ω. Let ρ = p

,... ,p

be a path of length l of population vectors in the sim-

plex Λ. The corresponding cost of this path is deﬁned

|ρ| =

∑

k=1

k−1

(43)

with

p,q

∑

k∈Ω

· ln



(G (p))



. (44)

,ω

Figure 10: Fixed point graph of the simple genetic algo-

rithm with α-selection as RHS τ.

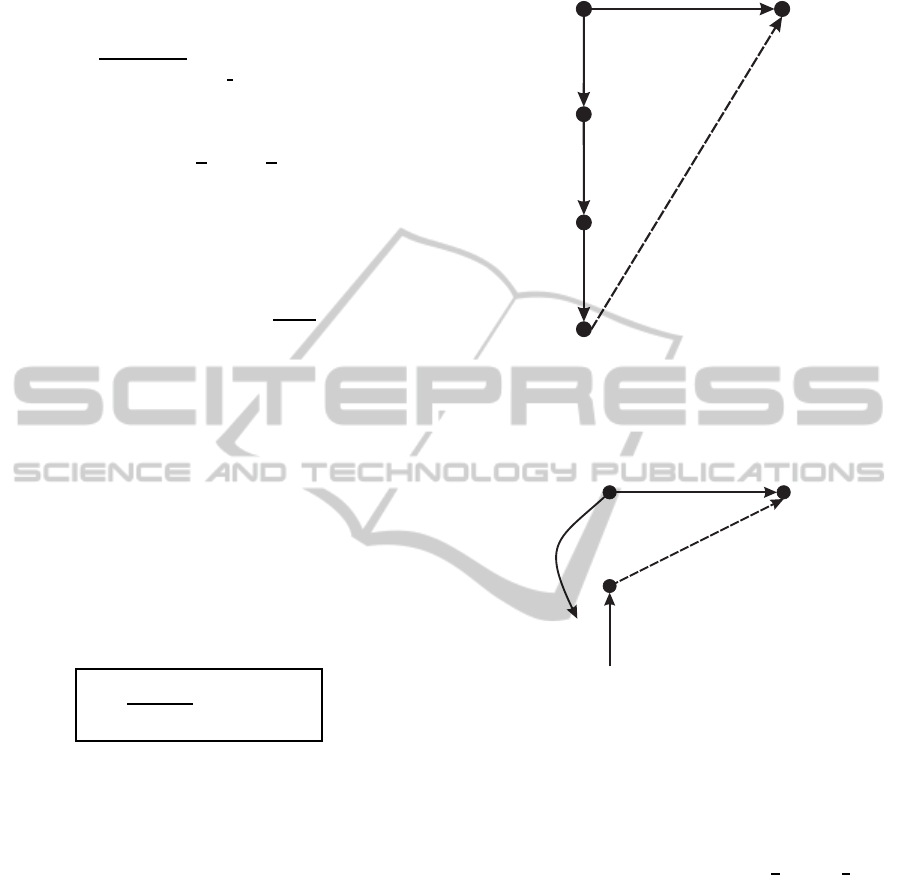
The ﬁxed point graph shown in Fig. 10 is deﬁned

as the complete directed graph on the set of stable

ﬁxed points F with weights

,ω

= inf



|ρ| : ρ is a path from ω

to ω



. (45)

For inﬁnite population size r → ∞ the steady state

distribution of the simple genetic algorithm as RHS

τ converges to the steady state distribution of the

Markov chain C over F . For the determination of

this steady state distribution we consider the so-called

tributary. The tributary T

is deﬁned as the tree con-

taining every vertex of F with all its edges pointing

towards the root ω

. The cost of the tributary T

given by the sum of its edge weights ρ

,ω

. As shown

by VOSE in (Vose, 1996; Vose, 1999b) for an inﬁnite

population size r → ∞ the steady state distribution of

the simple genetic algorithm is given by the root ω

the minimum cost tributary T

(provided it exists).

Due to the simple structure of the dynamical sys-

tem model of the simple genetic algorithm with α-

selection and its stable ﬁxed points ω

= σ

ω future

research will focus on the derivation of this steady

state distribution for the simple genetic algorithm

with α-selection. In view of the rapid convergence of

the simple genetic algorithm with α-selection, paths

ρ = ω

,p,ω

of length l = 2 from ﬁxed point ω

= σ

to ﬁxed point ω

= σ

ω with interior point p ∈ Λ are

considered. The corresponding cost of this path is

given by

|ρ| = α

+ α

p,ω

or equivalently

|ρ| =

∑

k∈Ω

· ln



(G (ω

))



(46)

∑

k∈Ω

(ω

)

· ln



(ω

)

(G (p))



By taking into account

G (ω

)

= (ω

)

= ω

i⊕k

(47)

and

(ω

)

= ω

j⊕k

(48)

if follows

|ρ| =

∑

k∈Ω

·ln



i⊕k



∑

k∈Ω

j⊕k

·ln



j⊕k

(G (p))



(49)

Under the simplifying assumption of paths ρ =

,p,ω

of length 2 the weights of the ﬁxed point

graph are then approximately given by

,ω

= inf

(

∑

k∈Ω

· ln



i⊕k



+ (50)

∑

k∈Ω

j⊕k

· ln



j⊕k

(G (p))



: p ∈ Λ

)

SIMPLE GENETIC ALGORITHM WITH a-SELECTION - Intrinsic System Model, Fixed Points and the Fixed Point

Graph

287

with

G (p)

∑

j∈Ω

· M

b⊕k, j⊕k

(51)

and

b = argmax{ f

: i ∈ Ω∧ p

> 0} . (52)

Future research will focus on the analytical derivation

of these weights ρ

,ω

and the determination of the

minimum cost tributary T

leading to the steady state

distribution ω

of the simple genetic algorithm with

α-selection.

6 CONCLUSIONS

The intrinsic system model for the simple genetic al-

gorithm with α-selection simpliﬁes the analysis of the

dynamical system model of genetic algorithms. It

is deﬁned by the mixing matrix M and enables the

derivation of the unique ﬁxed point ω. The simpli-

ﬁcations are gained because the ﬁtness function f is

hidden from the mathematical formulation by making

use of the α-individual b. Since b enters the dynam-

ical system model via a permutation σ

according to

· M

∗

· σ

the intrinsic system model can be formu-

lated with the help of the matrix M

∗

The intrinsic system model provides a means to

analyze the genetic algorithm’s exploitation and ex-

ploration of the search space Ω irrespective of the

ﬁtness function f. This model is compatible with

the equivalence relation imposed by schemata as

shown in (Neubauer, 2008a) by explicitly deriving

the coarse-grained system model for a given schemata

family. Experimental results for the simple genetic

algorithm with α-selection, uniform crossover and

bitwise mutation presented in this paper show close

agreement to the theoretical predictions with respect

to the rapid convergence of the permuted population

vector σ

p to the unique ﬁxed point ω obtained from

the intrinsic system model.

It is further conjectured that the structure of the

dynamical system model of the simple genetic algo-

rithm with α-selection and its intrinsic system model

simplify the determination of the steady state distri-

bution ω

based on the ﬁxed point graph and the min-

imum cost tributary T

. The analysis of the ﬁxed

point graph and the analytical derivation of its weights

,ω

will be the focus of future research.

REFERENCES

Holland, J. H. (1992). Adaptation in Natural and Artiﬁcial

Systems – An Introductory Analysis with Applications

to Biology, Control, and Artiﬁcial Intelligence. First

MIT Press Edition, Cambridge.

Neubauer, A. (2008a). Intrinsic system model of the genetic

algorithm with α-selection. In Parallel Problem Solv-

ing from Nature PPSN X, Lecture Notes in Computer

Science, pages 940–949. Springer.

Neubauer, A. (2008b). Theory of genetic algorithms with α-

selection. In Proceedings of the 1st IAPR Workshop on

Cognitive Information Processing – CIP 2008, pages

137–141.

Neubauer, A. (2008c). Theory of the simple genetic algo-

rithm with α-selection. In Proceedings of the 10th

Annual Genetic and Evolutionary Computation Con-

ference – GECCO 2008, pages 1009–1016.

Neubauer, A. (2009). Simple genetic algorithm with gen-

eralised α

⋆

-selection. In Proceedings of the Inter-

national Joint Conference on Computational Intelli-

gence – IJCCI I2009, pages 204–209.

Reeves, C. R. and Rowe, J. E. (2003). Genetic Algorithms

– Principles and Perspectives, A Guide to GA Theory.

Kluwer Academic Publishers, Boston.

Vose, M. D. (1996). Modeling simple genetic algorithms.

Evolutionary Computation, 3(4):453–472.

Vose, M. D. (1999a). Random heuristic search. Theoretical

Computer Science, 229(1-2):103–142.

Vose, M. D. (1999b). The Simple Genetic Algorithm – Foun-

dations and Theory. MIT Press, Cambridge.

Vose, M. D. and Wright, A. H. (1998). The simple ge-

netic algorithm and the walsh transform – part i, the-

ory – part ii, the inverse. Evolutionary Computation,

6(3):253–273, 275–289.

ICEC 2010 - International Conference on Evolutionary Computation

288