
THE
TYPHOON TRACK CLASSIFICATION USING TRI-PLOTS
AND MARKOV CHAIN
∗
John Chien-Han Tseng, Hsing-Kuo Pao
Research and Development Center, Central Weather Bureau, Taipei, Taiwan
Dept. of Computer Science & Information Engineering, National Taiwan University of Science & Technology, Taipei, Taiwan
Christos Faloutsos
Department of Computer Science, Carnegie Mellon University, Pittsburgh, PA, U.S.A.
Keywords:
Typhoon tracks, Trajectory data, ENSO, La Ni
˜
na, Tri-plots, Markov chain, Dissimilarity measure, Isomap,
SSVM.
Abstract:
We aim at understanding typhoon tracks by classifying them into the ENSO and La Ni
˜
na types. Two meth-
ods, namely, tri-plots and Markov chain combined with a novel dissimilarity measure for trajectory data are
proposed in this work. The calculation of the tri-plots can help us to separate ENSO from La Ni
˜
na year ty-
phoon tracks with the training error about 0.023 to 0.268 and the test error about 0.271 to 0.334. The Markov
chain based dissimilarity measure, combined with the SSVM classifier can help us to classify tracks with the
training error around 0.031 to 0.173 and the test error around 0.181 to 0.287. Moreover, for the purpose of
visualization, the tri-plots or Markov chain-based method maps the typhoon track data into low dimensional
space. In the space, the typhoon tracks of small dissimilarity should be regarded as one group. The map can
be very helpful for catching the hidden pattern of ENSO and La Ni
˜
na atmospheric circulation for establishing
typhoon databases. In general, we believe that tri-plots and Markov chain-based method are useful tools for
the typhoon track classification problem and should merit further investigation in related research community.
1 INTRODUCTION
It is an important and meaningful work of the typhoon
track classification which can be used to diagnose
the atmospheric circulations and establish typhoon
databases. Some researches (Camargo et al., 2007a;
Camargo et al., 2007b; Lee et al., 2007) focused on
the different shapes or the clusters of the typhoon tra-
jectories. It means that they divide the typhoon tra-
jectories into several groups; for example, the east-
westward movement typhoons, or the recurved move-
ment having more north-southward component move-
ment typhoons, or maybe the typhoons close to the
continent, or the typhoons trapped in some areas,
etc. In general, they describe typhoon tracks mostly
based on their intuition without too much theoreti-
cal support. The method of Lee et al. (Lee et al.,
∗
Research
partially supported by Taiwan National Sci-
ence Council Grant # 98-2221-E-011-105.
2007) sliced the typhoon tracks into different seg-
ments by different moving directions, and used the
minimum description length (MDL) to cluster the ty-
phoon tracks. The method of Camago et al. (Ca-
margo et al., 2007a; Camargo et al., 2007b) followed
Gaffney and Smyth (Gaffney and Smyth., 1999) tra-
jectory clustering with mixtures regression models,
and arranged the typhoon tracks into seven clusters.
The common point of these researches regards every
single typhoon track as one sequence. In this work,
we consider typhoon tracks by collecting the typhoon
cases for a period of time to find a global understand-
ing of the typhoon data. We examine the different
spatio-temporal structures of typhoon tracks for the
classification.
In atmosphere, the most significant annual circulation
variation events are ENSO (El Ni
˜
no southern oscilla-
tion) and La Ni
˜
na, the anti-ENSO. When the El Ni
˜
no
or ENSO event happens, the anomaly of equatorial
364
Chien-Han Tseng J., Pao H. and Faloutsos C..
THE TYPHOON TRACK CLASSIFICATION USING TRI-PLOTS AND MARKOV CHAIN.
DOI: 10.5220/0003114303640369
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 364-369
ISBN: 978-989-8425-28-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

sea surface temperature area will move to the central
Pacific Ocean and that definitely causes the typhoon
generation area eastward and changes the shapes of
typhoon tracks. The purpose of this study is to clas-
sify the typhoon trajectories in a period of time into
either El Ni
˜
no or La Ni
˜
na event.
The method of tri-plots (Traina et al., 2001) is one
popular data mining tool to find the patterns and re-
lationship between two large-scale, multidimensional
datasets. The tri-plots are composed of two self-
plots and one cross-plot. In the comparison of two
datasets through tri-plots, the two self-plots find the
patterns of two individual datasets and the cross-plot
finds the relationship between the two datasets. Tak-
ing each El Ni
˜
no and La Ni
˜
na event data in turn, we
can depict the distribution of each data cloud by self-
plots and measure the distance of two data clouds by
cross-plots. We then use the distances from cross-
plots as the input for Isomap (Isometric feature map-
ping) (Tenebaum et al., 2000) to find low-dimensional
embedding of the typhoon data. After that, in the low-
dimensional space, the smooth support vector ma-
chine (SSVM) with gaussian kernel (Lee and Man-
gasarian., 2001) is used to classify the typhoon data
into El Ni
˜
no or La Ni
˜
na event.
On the other hand, we propose a second method
for typhoon track classification. We use Markov
chain (Bishop, 2006; Lin, 2009) to extract the hid-
den patterns of typhoon trajectories. We model a se-
quence, a period of time typhoon tracks, by a Markov
chain model. The consecutive time steps of the ty-
phoon coordinates can be described by conditional
probabilities in the Markov model. Risi (Risi, 2004)
also use Markov chain to analyze hurricane tracks,
but we focus on the classification of typhoon tracks.
Moreover, we propose a novel dissimilarity measure
for a pair of sequences for typhoon track classifica-
tion. Given two sequences, the dissimilarity measure
computes how well a sequence is described by the
model for another sequence and vice versa. Similarly,
the dissimilarity distance that we computed can be the
distances of the Isomap and the SSVM with gaussian
kernel is used for the classification problem.
The remainder of this paper is organized as follows.
In Section 2, we introduce our typhoon dataset. Sec-
tion 3 and Section 4 in turn discuss the tri-plots and
the Markov chain-based dissimilarity measure for ty-
phoon track classification, followed by their exper-
iment results. Then, in Section 5, we further dis-
cuss the proposed methods and summarize our con-
clusions.
2 DATA
The typhoon trajectory data that we discuss are
from Japan Meteorological Agency (JMA). The data
recorded the western Pacific ocean which covers the
west of the longitude 180E to the east of the 100E ty-
phoon center movements (positions) and other obser-
vation variables, e.g., pressure, wind speed, etc. The
data features in this study include:
1. longitude,
2. latitude,
3. minimum pressure,
4. average high level (300 hPa) wind speed of the
typhoon center, and
5. topographical information.
We obtain the first four features from the JMA
database; while the last topographical information is
calculated to show how close the typhoon center is
from the continent. The point is: when typhoon
touches the land, the intensity will decrease dramat-
ically or even disappear. Typhoon cannot hold longer
on the land, so it will not penetrate into the land so far.
In brief, if the typhoon center is at land, we define the
distance is equal to 0. In contrast, the typhoon center
is at sea, the distances between the center and the land
are calculated. Currently, the JMA data recorded the
typhoon trajectories from 1951 to 2009. The time res-
olution is about three to six hours. Furthermore, the
high level Meteorological data are from National Cen-
ter for Environment Prediction (NCEP) reanalysis-2
data. We use higher level (300 hPa) wind data in this
study, because the higher level wind steer the typhoon
movement (Chan and Gray., 1982; Emanuel, 2005).
The ENSO years and the La Ni
˜
na years are based on
NOAAs (National Oceanic and Atmospheric Admin-
istration) definition by Ni
˜
no 3.4 index. In order to
use the NCEP reanalysis-2 data, we only focus on the
time events after 1980. There are seven ENSO years
corresponding to seven ENSO events and the labels
are set to be 1 and there are five La Ni
˜
na years as five
events and the labels are set to be −1 . We also have
ten neutral events which do not belong to either ENSO
or La Ni
˜
na group. The number of labelled dataset
is relatively small. In some occasions, we chop the
events into sub-events so that we can obtain the result
with more statistical meaning.
THE TYPHOON TRACK CLASSIFICATION USING TRI-PLOTS AND MARKOV CHAIN
365

3 CLASSIFICATION BASED ON
TRI-PLOTS
Traina et al. (Traina et al., 2001) proposed the tri-plots
based on fractal dimension to calculate the difference
between two datasets. Given two datasets A and B, the
tri-plots can help us to judge whether the two datasets,
in this case, the ENSO and La Ni
˜
na typhoon trajec-
tories, are from the same distribution. The tri-plots
include three kinds of plot tools:
1. self-plot ( for dataset A ),
2. self-plot ( for dataset B ), and
3. cross-plot ( for two datasets ).
For two datasets A and B, and the cross-plot function
is defined by
Cross
A,B
(r) = log
Ã
∑
i
C
A,i
C
B,i
!
, (1)
where C
A,i
( C
B,i
) is the number of points from set
A( B ) in the i-th cell, and r is the distance for the pair
of points. Hence, the cross-plot function is propor-
tional to the count of A-B pairs within distance r, and
the cross-plot is the plot of the cross-plot function ver-
sus log(r). Moreover, the self-plot function is defined
by
Sel f
A
(r) = log
µ
∑
i
C
A,i
·(C
A,i
−1)
2
¶
, (2)
and the self-plot is the plot of the self-plot function
versus log(r). If A is self similar, the self-plot of A
is close to a straight line and the slope is the intrin-
sic dimension of the set which is correlated with the
fractal dimension of the set (Belussi and Faloutsos.,
1995). In most situations, the cross-plot and self-plot
with log(r) are not linear, and we can use regression
method to determine the regression lines. We use
the line slopes to discuss the information between the
datasets A and B instead of the original data points.
The Study of Self-plots. As mentioned, the fea-
tures that we used in this study are longitude, lati-
tude, minimum pressure, u (300 hPa), v (300 hPa),
and the topography information. The slope and in-
tercept based on self-plot function is regarded as the
point coordinates in a space. Then, we plot all the
annual ENSO and La Ni
˜
na events in 2-D, as shown
in Figure 1. Basically, the ENSO points (red points)
and the La Ni
˜
na points (blue points in the middle) are
roughly separated into two groups. It is interesting to
take a close look of the point set in the intercept verse
slope space. In Figure 1, we find that the 8688 on the
top right and 9596 on the bottom left are two extreme
2.7 2.8 2.9 3 3.1 3.2 3.3 3.4 3.5
8.5
9
9.5
10
10.5
11
9596
0708
8485
9800
8889
0405
0203
9798
9495
9192
8688
8283
The distribution of (m,b) by 6−D (lon,lat,minp,u300,v300,Gauss_geo_dist) data points
slope
intercept
Figure 1: The slope and intercept of the tri-plots of typhoon
data. The longitude, latitude, minimum pressure, u (300
hPa), v (300 hPa) and topography effect are used in the ex-
periment. We can roughly observe that the ENSO points
(red points) and the La Ni
˜
na points (blue points in the mid-
dle) are separated into two groups.
events. The 8688 event locates around the large slope
and intercept area; on the contrary, the 9596 event are
found around the small slope and intercept area. Af-
ter checking with the original typhoon trajectories, we
find that the number of typhoon cases in 9596 is very
few and the number of cases is about 12 during this
period of time in contrast to other events. Meanwhile,
the number of typhoon cases in 8688 event is in nor-
mal situation, but it belongs to ENSO event and the
typhoons seem to travel longer distances than others.
When we use the distance to calculate the tri-plots,
the longer distances we get, the larger slope we have.
This explains why the 8688 event has large slope and
intercept and the 9596 event has small slope and in-
tercept.
We can check the Figure 1 following the vertical line
with the same slope; for example, along the lines
slope = 2.85 and slope = 3.1. There are two events,
9798 and 0203, located around the 2.85 slope; sim-
ilarly, there are two events, 8889 and 9800 located
around the 3.1 slope. When we check the typhoon
trajectories, it is easy to find that the 8889 and 9800
events are very similar, and the 9798 and 0203 events
are very similar, too. As we know, the slope repre-
sents the fractal dimension, and the same fractal di-
mension of two data clouds implies that they are self-
similar. The different intercept but the same slope de-
picts that there are still differences in real geometrical
shapes; for example, a line and a circle (or a ring, i.e.,
without the inside part) have the same fractal dimen-
sion but different shapes. Based on this, the self-plot
distribution can afford a tool for atmospheric scien-
tists to do cluster studies.
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
366

The Study of Cross-plot. We would like to use
cross-plot to separate two types of data, the ENSO
and the La Ni
˜
na typhoon trajectories. Based on
the same set of features, the output from the cross-
plot functions is regarded as the distances for the
Isomap. In Isomap (Tenebaum et al., 2000), we 1)
construct a neighborhood graph by linking each pair
of events/points that qualify as neighbors; 2) find the
length of the shortest path between each pair of points
and take it as the approximation of their geodesic dis-
tance; and 3) take the pairwise (geodesic) distances
as the input and apply Multidimensional Scaling (or
MDS) to find the global Euclidean coordinates of
the points. Because there are only 12 labeled events
(seven ENSO, five La Ni
˜
na) in our study, it is not
so meaningful to operate the Isomap or the classifi-
cation task based on such a small dataset. We split
the dataset from 12 events to 60 events by chopping
each of the original event into five smaller sub-events.
In here, we carefully chop the event so that one ty-
phoon case is still kept in the same event. We set
the intrinsic dimensionality (Tenebaum et al., 2000)
equal to five for Isomap, then classify the events by
SSVM in the embedded space produced by Isomap.
As shown in Table 1, the classification results are:
training error around 0.023-0.268 and the test error
about 0.271-0.334, for different k’s for the nearest
neighbor choice.
Table 1: Error rates of the SSVM combined with cross-plots
and Isomap, for k equal to 5 to 10 which specifies the num-
ber of closest neighbors used in the Isomap.
P
P
P
P
P
P
P
SSVM
k
5 6 7 8 9 10
training err. 0.27 0.03 0.12 0.03 0.02 0.03
test err. 0.33 0.27 0.36 0.29 0.32 0.33
4 CLASSIFICATION BASED ON
MARKOV CHAIN AND A
DISSIMILARITY MEASURE
We assume the typhoon trajectories can be repre-
sented as a sequence s = (x
1
,x
2
,...,x
t
,...,x
T
), where
x
t
is the coordinate value of typhoon center composed
of longitude and latitude at time t; the subscripts 1, 2,
. . . , T mean the different time stamps of the typhoon
positions. Then, we define the pace vector x
t+1
−x
t
,
and the Euclidean pace size λ
t
= kx
t+1
−x
t
k. So the
pace change is given by 4λ
t
= λ
t+1
−λ
t
. The angle
θ
t
is defined by the angle between vector x
t+1
−x
t
and the x-axis; and the angle change is given by
4θ
t
= θ
t+1
−θ
t
. Let m(σ
λ
,σ
θ
) denote the model
of trajectory sequence, and the transition parameters
are σ
λ
, σ
θ
which represent the standard deviation
of pace changes and angle changes. According to
Markov chain theory, the probability density func-
tion of 4λ
t
and 4θ
t
or the probability of having x
t+2
given x
t+1
,x
t
can be described by
p(4λ
t
) ∼ N(4λ
mean
,σ
2
λ
)
=
1
√
2πσ
λ
exp
µ
−
(4λ
t
−4λ
mean
)
2
2σ
2
λ
¶
,
(3)
p(4θ
t
) ∼ N(4θ
mean
,σ
2
θ
)
=
1
√
2πσ
θ
exp
µ
−
(4θ
t
−4θ
mean
)
2
2σ
2
θ
¶
.
(4)
The log-likelihood `(s ; m) associated with trajectory
s and model m is written as
`(s; m) = log L(s ; m)
=log
µ
p(x
1
)p(x
2
|x
1
)
∏
t=1
P(x
t+2
|x
t
,x
t+1
)
¶
=log p(x
1
) + log p(x
2
|x
1
) +
∑
t=1
log(P(x
t+2
|x
t
,x
t+1
)).
(5)
We compute the (Shannon) code length of the trajec-
tory s as the negative log-likelihood as
c(s|m) = −`(s ; m) = −logL(s ; m). (6)
Finally, the dissimilarity value d is given by
d(s
1
,s
2
) =
1
2
µ
c(s
1
|m
2
)
c(s
2
|m
2
)
+
c(s
2
|m
1
)
c(s
1
|m
1
)
¶
. (7)
In this equation, it estimates how effective if we want
to describe one trajectory by the model for other tra-
jectory. The dissimilarity matrix D can be given af-
ter calculating all the trajectory pairs d(s
i
,s
j
). In this
study, in order to have representative typhoon trajec-
tories and save computing time, we combine several
typhoon tracks to be one trajectory. Because of com-
bining a period time typhoon trajectories as one se-
quence, the pace size between the ending point of one
trajectory and the beginning point of another trajec-
tory is larger than the regular pace sizes of consecu-
tive time stamps. We can choose the threshold with
4λ = 10 and ignore all the pace sizes of 4λ > 10.
We can compute two dissimilarity matrices D
4λ
and
D
4θ
based on two separated information about pace
size and angle and combine them into one target dis-
similarity as follows
D
target
= αD
4λ
+ (1 −α)D
4θ
, 0 ≤ α ≤1 (8)
In the formula, we can choose a larger α to respect
more of the importance of pace size information. In
THE TYPHOON TRACK CLASSIFICATION USING TRI-PLOTS AND MARKOV CHAIN
367
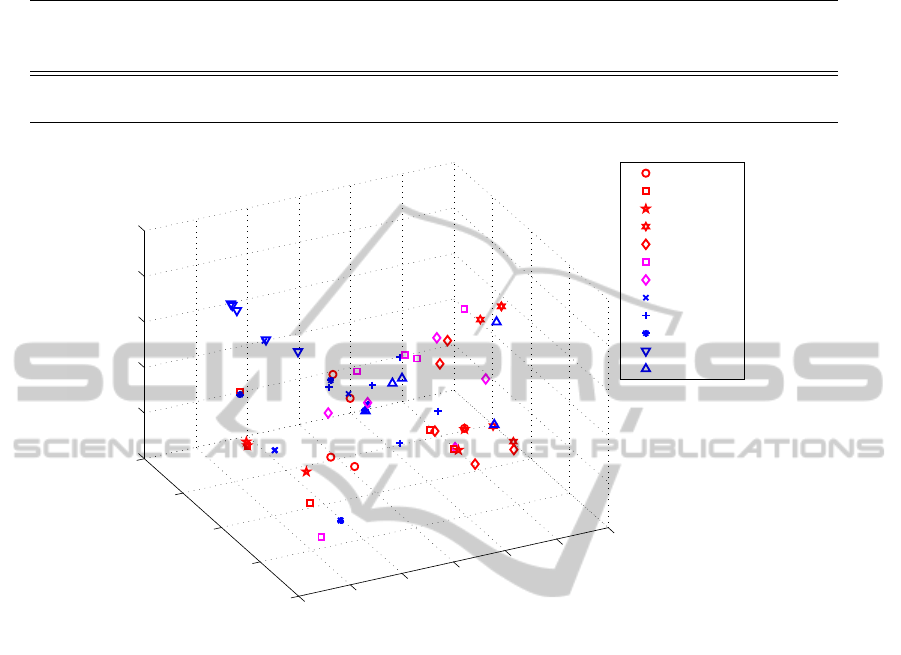
Table 2: The error rates of the SSVM based on Markov chain combined with the dissimilarity measure, with threshold
4λ ≤ 10 and k = 4 for the Isomap.
P
P
P
P
P
P
P
SSVM
α
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
training err. 0.17 0.05 0.14 0.06 0.16 0.17 0.15 0.04 0.03 0.04 0.05
test err. 0.28 0.25 0.25 0.22 0.29 0.29 0.28 0.20 0.18 0.20 0.25
−6
−4
−2
0
2
4
6
−4
−2
0
2
4
−2
−1
0
1
2
3
enso0203
enso0405
enso8283
enso8688
enso9192
enso9495
enso9798
lanina0708
lanina8485
lanina8889
lanina9596
lanina9800
Figure 2: The 3-D structure from Isomap with k=4 based on the threshold 4λ ≤ 10 for the Markov Chain-based experiments,
with α = 0.8 in the dissimilarity matrix calculation.
Table 2, we can find how different α’s can affect the
result. Again, we use SSVM following the Isomap for
the evaluation.
We want to compare the classification result based on
tri-plots and the result combining the Markov chain
and the proposed dissimilarity measure. We separate
the original 12 events into 60 events using the same
data splitting method as the previous section. The
dissimilarity matrix D forms these 60 trajectories can
the input for the Isomap. Again, executing the SSVM
with the intrinsic dimensionality chosen to be five for
Isomap. The result is shown in Figure 2 and Table 2.
In Figure 2, we show the 3-D structure from Isomap.
The La Ni
˜
na 9596 event located around left corner
with blue inverse triangle is the most different case
from the ENSO 8688 or ENSO 8283, and this result
is consistent with the tri-plots (Figure 1). Moreover,
the blue mark points on top left corner in Figure 2 are
from parts of La Ni
˜
na cases like 8485, 8889, 9800
and 0708 which somehow show the trajectories close
to Asian continent. Based on 10-fold cross validation,
the training error is 0.031-0.173 and the test error is
around 0.181-0.287.
5 CONCLUSIONS AND FUTURE
WORKS
In this study, we proposed the quantitative and objec-
tive tools, tri-plots and Markov chain-based method,
to distinguish the differences between the different
yearly typhoon track events. Based on the evaluation,
we have about 70% accuracy on classifying the ty-
phoon tracks belonged to El Ni
˜
no or La Ni
˜
na events.
In tri-plots, we afford a global view to see different
annual events by the self-plot distribution, and the re-
sult is consistent with the report of World Meteoro-
logical Organization (World Meteorological Organi-
zation, 2009), that is, no two El Ni
˜
no events are iden-
tical. Moreover, the self-plot distribution affords the
information for future clustering studies of El Ni
˜
no
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
368

and La Ni
˜
na events. Besides, the tri-plots experiments
tell us what kind of features we probably should have
them included for the classification or for typhoon
databases. Until now, the world typhoon databases
just store the low level features of typhoons. We be-
lieve that adding the high level winds or the consid-
eration of topographical effect should be included in
typhoon databases. On the other hand, the Markov
chain-based model gives us better performance than
the tri-plots. However, the different probability dis-
tributions should be considered in the future, that is,
Markov chain-based model still has more potential to
do the following classification researches. Finally, ei-
ther tri-plots or different Markov chain models, can
be extended to other traditional Meteorological data
analysis. Because the quantity of the Meteorologi-
cal is very large; for example, the space resolution
of NCEP reanalysis data is about 144×73 in hori-
zontal; the 17 layers in vertical for one specific fea-
ture and the time resolution is about 4 times in one
day. So, when we extend our methods to analyze the
annual events, we need to modify our current algo-
rithm. First, we need an alternative method to solve
the eigenproblem in Isomap (solving large and sparse
matrix), and we need more efficiency box-counting
data structure in tri-plots.
REFERENCES
Belussi, A. and Faloutsos., C. (1995). Estimating the se-
lectivity of spatial queries using the correlation fractal
dimension. pages 299–310. In the 21-th conference of
Very Large Data Bases.
Bishop, C. M. (2006). Pattern recognition and machine
learning. Springer press.
Camargo, S, J., Robertson, A. W., Gaffney, S. J., and Smyth,
P. (2007a). Cluster analysis of typhoon tracks. Part
I: general properties. Journal of Climate, 20:3635–
3653.
Camargo, S, J., Robertson, A. W., Gaffney, S. J., and Smyth,
P. (2007b). Cluster analysis of typhoon tracks. Part
II: large circulation and ENSO. Journal of Climate,
20:3654–3676.
Chan, J. C. L. and Gray., W. M. (1982). Tropical cy-
clone movement and surrounding flow relationships.
Monthly Weather Review, 100:1354–1374.
Emanuel, K. (2005). Divine wind: the history and science
of hurricanes. Oxford university press.
Gaffney, S. and Smyth., P. (1999). Trajectory clustering
with mixtures of regression models. pages 63–72. In
the International Conference on Knowledge Discov-
ery and Data Mining.
Harr, P. A. and Elsberry, R. L. (1991). Tropical cy-
clone track characteristics as a function of large-
scale circulation anomalies. Monthly Weather Review,
119:1448–1468.
Hsieh, W. (2009). Machine learning methods in the envi-
ronmental sciences. Cambridge university press.
Jordan, M. I. An introduction to probabilistic graphic mod-
els. In preparation.
Lee, J.-G., Han, J., and Whang., K.-Y. (2007). Trajectory
clustering: A partition-and-group framework. pages
593–640. International Conference on Management of
Data.
Lee, Y.-J. and Mangasarian., O. L. (2001). SSVM:
A smooth support vector machine for classification.
Comput. Optim. Appl., 20(1):5–22.
Lin, H. (2009). Trajectory based on behavior analysis for
verification and recognition. Master’s thesis, National
Taiwan University of Science and Technology, master
thesis, Taipei.
Miller, J., Weichman, P. B., and Cross, M. C. (1992). Statis-
tical mechanics, eulers equation, and jupiters red spot.
Physics Review, A45:2328–2359.
Risi, C. (2004). Statistical synthesis of tropical cyclone
tracks in a risk evaluation perspective. Technical re-
port, Massachusetts Institute of Technology, intern-
ship report, Cambridge.
Strogatz, S. H. (2001). Nonlinear dynamics and chaos: with
applications to Physics, Biology, Chemistry, and engi-
neering. Westview press.
Tenebaum, J. B., d. Silva, V., and Langford., J. C. (2000). A
global geometric framework for nonlinear dimension-
ality reduction. Science, 290:2319–2323.
Traina, A., Traina, C., Papadimitriou, S., and Faloutsos, C.
(2001). Tri-plots: Scalable tools for multi dimensional
data. pages 184–193. In the International Conference
on Knowledge Discovery and Data Mining.
Vlachos, M., Gunopulos, D., and Kollios, G. (2002). Dis-
covering similar multidimensional trajectories. pages
673–684. In the International Conference on Data En-
gineering.
Wang, B., Rui, H., and Chan, J. C. L. (2002). How strong
ENSO events affect tropical activity over the western
north pacific. Journal of Climate, 15:1643–1658.
Webster, P. J., Holland, G. J., Curry, J. A., and Chang., H.-
R. (2005). Changes in tropical cyclone number, dura-
tion, and intensity in a warming environment. Science,
309:1844–1846.
World Meteorological Organization (2009). El Ni
˜
no/La
Ni
˜
na update. Technical report, World Meteorological
Organization.
THE TYPHOON TRACK CLASSIFICATION USING TRI-PLOTS AND MARKOV CHAIN
369
