
TOWARDS LEARNING WITH OBJECTS
IN A HIERARCHICAL REPRESENTATION
Nicolas Cebron
Multimedia Computing Lab, University of Augsburg, Universitaetsstr. 6a, 86159 Augsburg, Germany
Keywords:
Supervised learning, Active learning, Object hierarchy.
Abstract:
In most supervised learning tasks, objects are perceived as a collection of fixed attribute values. In this work,
we try to extend this notion to a hierarchy of attribute sets with different levels of quality. When we are given
the objects in this representation, we might consider to learn from most examples at the lowest quality level
and only to enhance a few examples for the classification algorithm. We propose an approach for selecting
those interesting objects and demonstrate its superior performance to random selection.
1 INTRODUCTION
Mapping input examples to a desired continuous or
categorical output variable is the goal of supervised
learning.To achieve this, the learner has to general-
ize from the presented examples to yet unseen exam-
ples. We have seen numerous algorithms in the field
of machine learning that deal with this issue. They
share the property that the objects of interest are de-
scribed by a given number of attribute values (the so-
called feature vectors). This representation may be a
good choice to describe most of the objects that we
encounter in real-world classification tasks. However,
we have seen that in some circumstances a different
object representation may be useful, e.g. in the do-
main of graph mining or structure mining.
In this work, we want to enhance the representa-
tion of objects in such a way that we use only as much
information from each object as is needed for the clas-
sification task at hand. To make this possible, we sug-
gest to represent objects in a hierarchy that is com-
posed of different levels of quality. The underlying
idea of this approach is that we do not need to com-
pute the best representation for all objects. We argue
that it is sufficient to learn a classifier on the lower
quality level and use a selection strategy to enhance
”useful” objects. This setting is very useful whenever
we have limited resources to compute a full feature
representation of an object, especially in real-time ap-
plications (e.g. robotics). We argue that many objects
from different domains (classification of images, mu-
sic or 3D objects) can be described on different levels
of quality.
Our idea is very related to the concept of Active
Learning (Cohn et al., 1994). However, in this work,
we do not try to select objects that will be labeled
by a human expert. Instead, we try to select objects
that will be enhanced for the classification algorithm.
There are two related approaches (Zheng and Pad-
manabhan, 2002) (Saar-Tsechansky et al., 2009) that
deal with obtaining more feature values for a subset
of objects. Although they follow a similar idea, the
key difference to our work lies in the representation
of objects. We propose a hierarchical representation
over several levels. To the best of our knowledge, this
is a completely new approach in the supervised ma-
chine learning setting.
2 LEARNING WITH SVM
In this section, we introduce the underlying Support
Vector Machine (SVM) classification algorithm be-
fore turning to the selection strategy. Given a set of la-
beled training data D = {(~x
1
,y
1
),(~x
2
,y
2
),...,(~x
m
,y
m
)
where ~x
i
∈ R
N
and y
i
∈ {−1,+1}, a linear
SVM (Sch
¨
olkopf et al., 1999) is defined in terms of
its hyperplane
w ·~x + b = 0 (1)
and its corresponding decision function
f (~x) = sgn(w ·~x + b) (2)
for w ∈ R
N
and b ∈ R. Among all possible hyper-
planes that separate the positive from the negative ex-
amples, the unique optimal hyperplane is the one for
326
Cebron N..
TOWARDS LEARNING WITH OBJECTS IN A HIERARCHICAL REPRESENTATION.
DOI: 10.5220/0003114403260329
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2010), pages 326-329
ISBN: 978-989-8425-28-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

which the margin is maximized:
max
w,b
{min
~x
i
{||~x −~x
i
|| :~x ∈ R
N
,w ·~x + b = 0}} (3)
As the training data is not always separable, a soft
margin classifier uses a misclassification cost C that
is assigned to each misclassified example. Equation 3
is optimized by introducing Lagrange multipliers α
i
and recasting the problem in terms of its Wolfe dual:
maximize: L
D
=
∑
i
α
i
−
1
2
∑
i, j
α
i
α
j
y
i
y
j
~x
i
~x
j
subject to: 0 ≤ α
i
≤ C, and
∑
i
α
i
y
i
= 0
(4)
All ~x
i
for which the corresponding α
i
is non-zero are
the support vectors.
The support vectors limit the position of the opti-
mal hyperplane. The objects ~x
i
for which α
i
= C are
the bound examples, which are incorrectly classified
or are within the margin of the hyperplane.
3 OBJECT SELECTION
In this work, we assume that we have j views of de-
scending quality V
u
,u = 1,..., j. The best level is de-
noted by V
1
and the worst by V
j
. We describe the ob-
ject~x in view j as V
j
(~x). Note that all~x
i
in the training
set are still in R
N
(the number of attributes does not
change).The training set at any point in time t consists
of the objects - each object at a different view level:
D = {(V
1
(~x
1
),y
1
),(V
2
(~x
2
),y
2
),. .. , (V
m
(~x
m
),y
m
). At
t = 0, all objects are only given in the worst view V
j
.
At any time point t we want to enhance some ob-
jects in order to have more detailed information for
the classification algorithm. We consider this as an
iterative setting, where we train a classifier, enhance
some objects, and then train the classifier on the new
training set.
Enhancing an object means we get a better esti-
mate of where this object lies in the current feature
space. Intuitively, if we have trained a classifica-
tion algorithm on a dataset, enhancing objects that are
classified with high confidence will not provide much
information for the classifier.
Instead, we propose to select objects that are close
to the decision boundary of the current classifier.
These are the objects that are classified with low con-
fidence. We expect that a more detailed information
about the exact position of this object in this feature
space provides the most information for the classifier.
This idea is very related to the concept of uncertainty
sampling in Active Learning (e.g. in the works of
(Schohn and Cohn, 2000), (Campbell et al., 2000) and
(Tong and Koller, 2001)). In the future, it might be in-
teresting to look at other selection strategies from this
domain, e.g. version space reduction.
The preceding works have used a Support Vec-
tor Machine (SVM) classifier and ranked objects ~x
by their distance to the dividing hyperplane, which
is given by the normal vector w and offset b:
min
~x
|w ·~x + b| (5)
The goal is to maximally narrow the existing margin
with an object.
Our proposed algorithm works as follows: all ob-
jects are given at the lowest view level in the begin-
ning. We train a SVM classifier and use Equation 5 to
rank objects. We can then select the top n objects for
enhancement and add the improved examples to the
current training set. This continues until we are sat-
isfied with the results or we do not have more budget
left to enhance further examples.
4 EXPERIMENTS
4.1 Artificial Data
To demonstrate the principle of operation and the po-
tential benefit of the proposed algorithm, we have
chosen a dataset that is easy to visualize. We have
generated a two-dimensional dataset with two classes
with a banana shaped distribution. The data is uni-
formly distributed along the bananas and is super-
imposed with a normal distribution with a standard
deviation s in all directions. The class priors are
P(1) = P(2) = 0.5.
Two views have been created: a good view V
1
(see
Figure 1(a)) by using a small standard deviation and a
bad view V
2
(Figure 1(b)) with a large standard devia-
tion. As can be seen, V
2
is very noisy, but the underly-
ing concept of two opposed banana shapes is still the
same. We have used a SVM with a RBF kernel; the γ
parameter has been set to 2.0. The SVM classifier is
plotted as a solid black line. The classification in view
V
1
reflects our ground truth and is therefore plotted as
a dotted black line in the other views in Figure 1.
Due to the high standard deviation, the classifica-
tion in view V
2
is far from optimal. In this experi-
ment, we have improved 30 examples. We plot the
improved dataset and the corresponding classifier that
is learned in this new data space. Figure 1(c) shows
the new dataset and classifier with our Active Algo-
rithm and Figure 1(d) shows the new dataset and clas-
sifier with randomly improved examples.
We can observe that the strategy of choosing ex-
amples close to the decision boundary results in a bet-
TOWARDS LEARNING WITH OBJECTS IN A HIERARCHICAL REPRESENTATION
327
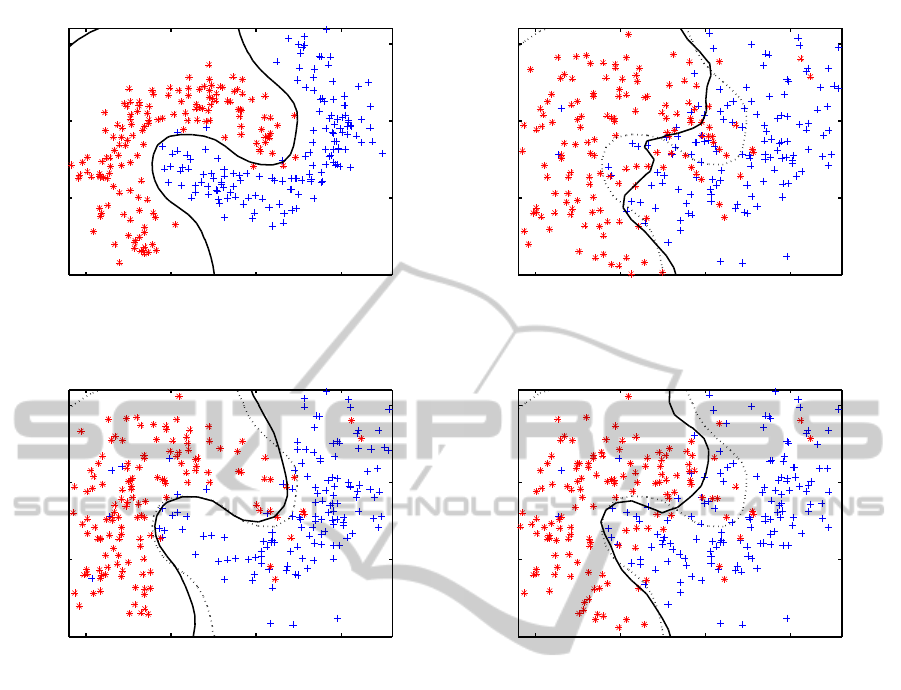
−10 −5 0 5
−10
−5
0
5
Feature 1
Feature 2
Banana Dataset View 1
(a) Banana Dataset View 1 (s = 1).
−10 −5 0 5
−10
−5
0
5
Feature 1
Feature 2
Banana Dataset View 2
(b) Banana Dataset View 2 (s = 2.5).
−10 −5 0 5
−10
−5
0
5
Feature 1
Feature 2
AAA Improvement
(c) Improved Dataset with our Active Algorithm.
−10 −5 0 5
−10
−5
0
5
Feature 1
Feature 2
Random Improvement
(d) Improved Dataset with Random Adaption.
Figure 1: Banana Dataset in two views of different quality (top). The black line represents the classifier in each view. The
classifier of View 1 is plotted as a dotted black line in the other views.
ter classification accuracy than random improve-
ment. Random improvement will eventually reach the
same performance but needs more examples to do so.
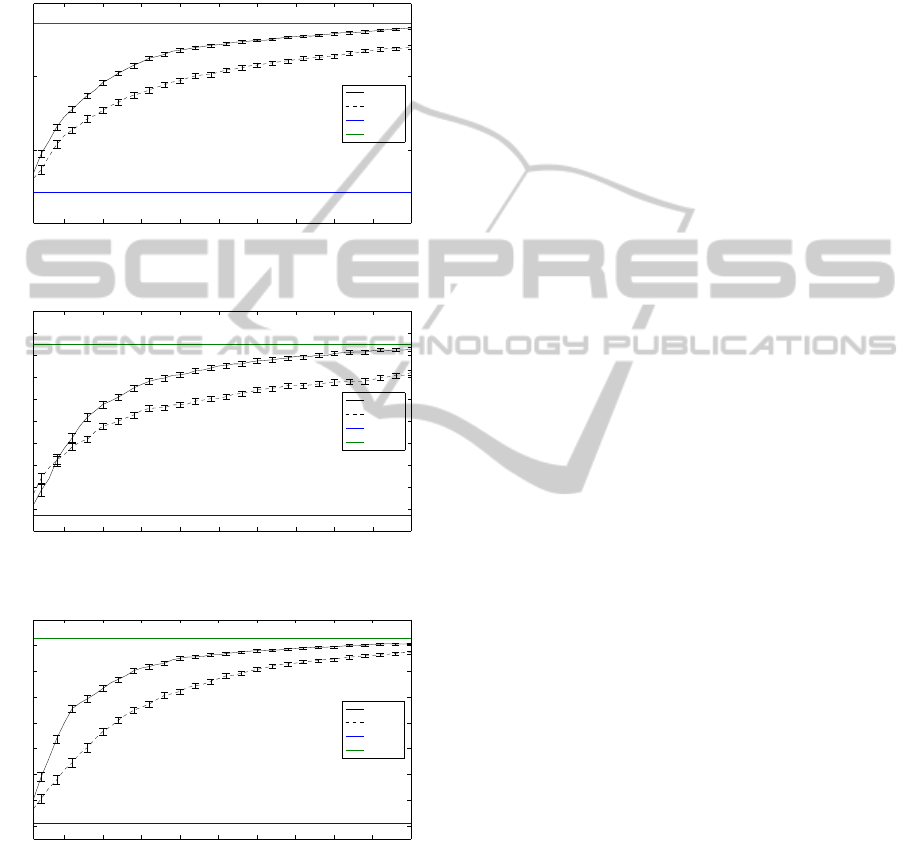
4.2 Numbers Dataset
The multiple features dataset from the UCI Machine
Learning Repository (Asuncion and Newman, 2007)
consists of features of handwritten numerals (’0’-
’9’). extracted from a collection of Dutch utility
maps.We have computed two views on these objects:
the Zernike Moments based on the original image of
size 16x16 (Level 2, green line) and of a subsampled
image of size 8x8 (Level 1, red line). We compare our
Adaptive refinement strategy against Random refine-
ment, a strategy that improves a randomly chosen set
of examples in each training iteration (dotted line).
Each experiment has been repeated 100 times. In
each iteration, we split up the dataset randomly and
use 40% for training and 60% for testing.
All training instances are first assumed to have the
lowest quality V
1
. A batch of examples is selected
in each iteration (plotted on the x-axis) and the mean
classification accuracy (given the ground truth in the
testing data on the highest view level V
j
) is plotted
on the y-axis. We also plot the mean accuracy of a
classifier on each view level.
We have chosen three binary classification tasks:
’1’ vs ’5’ in Figure 2, ’3’ vs ’8’ in Figure 3 and ’5’ vs
’7’ in Figure 4. As can be seen, the Adaptive strategy
clearly outperforms Random improvement of exam-
ples.
5 CONCLUSIONS
In this work, we have proposed a new learning setting,
where the objects of interest can be obtained at differ-
ing quality levels. We have proposed a new scheme
that improves a few selected examples with a SVM as
KDIR 2010 - International Conference on Knowledge Discovery and Information Retrieval
328
hspace-0.39cmthe underlying classifier. Objects
are ranked by their distance to the separating hyper-
plane to select a subset that is enhanced in each it-
eration. Experiments on an artificial dataset and a
dataset from the UCI repository of machine learning
have shown that this is a promising approach. Future
5 10 15 20 25 30 35 40 45 50
0.85
0.9
0.95
1
Iterations
Accuracy
Adaptive
Random
Level 1
Level 2
Figure 2: Test accuracy ’1’ vs. ’5’.
5 10 15 20 25 30 35 40 45 50
0.9
0.91
0.92
0.93
0.94
0.95
0.96
0.97
0.98
0.99
1
Iterations
Accuracy
Adaptive
Random
Level 1
Level 2
Figure 3: Test accuracy ’3’ vs. ’8’.
5 10 15 20 25 30 35 40 45 50
0.84
0.86
0.88
0.9
0.92
0.94
0.96
0.98
1
Iterations
Accuracy
Adaptive
Random
Level 1
Level 2
Figure 4: Test accuracy ’5’ vs. ’7’.
work needs to be done in the following areas: it would
be interesting to have a cost model and a fixed budget
to describe the costs that are involved in the enhance-
ment of objects. More experiments need to be carried
out on different data sets. It would be interesting to
take the current view level into account when objects
are ranked. At last, more strategies from the domain
of Active Learning need to be tested in this setting.
As can be seen, this new notion of objects in a hierar-
chy raises several interesting research questions and
is worth to be further explored.
ACKNOWLEDGEMENTS
This work was developed at the International Com-
puter Science Institute in Berkeley and supported by a
fellowship within the Postdoc-Programme of the Ger-
man Academic Exchange Service (DAAD).
REFERENCES
Asuncion, A. and Newman, D. (2007). UCI machine learn-
ing repository.
Campbell, C., Cristianini, N., and Smola, A. J. (2000).
Query learning with large margin classifiers. In ICML
’00: Proc. of the Seventeenth International Confer-
ence on Machine Learning, pages 111–118, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Cohn, D. A., Atlas, L., and Ladner, R. E. (1994). Improving
generalization with active learning. Machine Learn-
ing, 15(2):201–221.
Saar-Tsechansky, M., Melville, P., and Provost, F. (2009).
Active feature-value acquisition. Management Sci-
ence, 55(4):664–684.
Schohn, G. and Cohn, D. (2000). Less is more: Active
learning with support vector machines. In Langley, P.,
editor, ICML, pages 839–846. Morgan Kaufmann.
Sch
¨
olkopf, B., Burges, C. J. C., and Smola, A. J., editors
(1999). Advances in kernel methods: support vector
learning. MIT Press, Cambridge, MA, USA.
Tong, S. and Koller, D. (2001). Support vector machine
active learning with applications to text classification.
Journal of Machine Learning Research, 2:45–66.
Zheng, Z. and Padmanabhan, B. (2002). On active learning
for data acquisition. In ICDM ’02: Proceedings of the
2002 IEEE International Conference on Data Mining,
page 562, Washington, DC, USA. IEEE Computer So-
ciety.
TOWARDS LEARNING WITH OBJECTS IN A HIERARCHICAL REPRESENTATION
329
