MULTIPLE KERNEL LEARNING FOR ONTOLOGY INSTANCE
MATCHING
Diego Ardila, Jos
´
e Abasolo and Fernando Lozano
Universidad de los Andes, Bogot
´
a, Colombia
Keywords:
Ontology instance matching, Similarity measure combination, Multiple kernel learning, Indefinite kernels.
Abstract:
This paper proposes to apply Multiple Kernel Learning and Indefinite Kernels (IK) to combine and tune
Similarity Measures within the context of Ontology Instance Matching. We explain why MKL can be used in
parameter selection and similarity measure combination; argue that IK theory is required in order to use MKL
within this context; propose a configuration that makes use of both concepts; and present, using the IIMB
bechmark, results of a prototype to show the feasibility of this idea in comparison with other matching tools.
1 INTRODUCTION
Ontology matching is the problem of determining cor-
respondences between concepts, properties, and in-
dividuals of two or more different formal ontologies
(Euzenat and Shvaiko, 2007). The aforementioned
plays a key role in many different applications such
as data integration, data warehousing, data transfor-
mation, open government, peer-to-peer data manage-
ment, semantic web, and semantic query processing.
Currently, one of its main challenges is the selec-
tion and combination of similarity measures during
the matching process (Shvaiko and Euzenat, 2008).
Although it is broadly accepted that multiple similar-
ity measures can help in finding better alignments and
the general opinion supports the idea that there is not a
similarity measure that is able to deal with all existing
matching problems, we still require to find ways to or-
chestrate the available similarity measures in order to
find the appropriate set of these for the matching task
at hand.
Furthermore, even if it is possible to choose the
measures that are likely to work within a specific con-
text, the question on how to set the parameters of such
functions remains open. Empirical results and litera-
ture tell us that similarity measures work but they re-
quire prior tuning steps.
To overcome these issues, most of the current
proposals use probabilistic or machine learning tech-
niques in order to find the correct combination of
measures. This is a natural approach considering that
the rules that define how the measures should be com-
posed depend on the real application. Furthermore,
even for a domain expert, such rules are not necessar-
ily clear because similarity for humans is a relative -
and sometimes - contradictory concept (Laub et al.,
2007). Within this context, a learning algorithm is a
suitable option to find such rules.
In the present paper, our aim is to give new in-
sights to this problem. We propose a matching solu-
tion based on the recent research in Multiple Kernel
Learning (MKL) and Indefinite Kernels (IK). To our
knowledge, there are not any current solutions that
propose the use of the algorithms and techniques that
are employed in this article. Our main concern is to
explore other ways to find the weights that typically
need to be determined when a process of aggregation
of similarity measures is carried on; therefore, we as-
sume the existence of an available library of similarity
measures and aggregation functions from which both
of these can be selected.
In a proof of concept prototype, the semi-
supervised learning paradigm is also integrated, as
we believe it to be suitable for this problem. First,
because of the volume of instances it is not feasible
to compare all the possible instances to find the cor-
rect correspondences; for this reason, it is necessary
to find rules that can be learned from a small subset of
instances. Second, as previously stated, the rules that
make two instances equivalent can be difficult to cap-
ture, thus, the use of a learning algorithm to find them
is better. Third, a huge amount of unlabeled data can
be easily obtained in many applications of this prob-
lem so it would be great if we could take advantage of
such information.
This article is organized as follows: In the next
311
Ardila D., Abasolo J. and Lozano F..
MULTIPLE KERNEL LEARNING FOR ONTOLOGY INSTANCE MATCHING.
DOI: 10.5220/0003117403110318
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2010), pages 311-318
ISBN: 978-989-8425-29-4
Copyright
c
 2010 SCITEPRESS (Science and Technology Publications, Lda.)

section some of the related work is described. Sec-
tion 3 discusses the suggested approach. Section
4 presents experimental results that validate our ap-
proach. Finally, Section 5 discusses the conclusions
and future work.
2 BACKGROUND AND RELATED
WORK
There is a lot of work related to ontology match-
ing. Some of the available reviews are (Kalfoglou
and Schorlemmer, 2005) and (Shvaiko and Shvaiko,
2005). However, these reviews focus on the schema
level. This is probably because there are relatively
few works that prioritize the instance level. In fact, to
our knowledge, there is not a comprehensive review
involving ontology instance matching systems.
Specifically, concerning the challenge of tuning
and selecting similarity measures, the proposals typ-
ically attempt to find a linear combination
∑
c
i
S
i
,
where each S
i
is a similarity measure which some-
times is called a matcher, an agent, an expert or a clas-
sification hyphotesis. What tends to change within the
different works is the manner in which the coefficients
are found.
One of the first solutions proposed was using val-
ues obtained through empirical evaluation. For exam-
ple, this approach was used by (Castano et al., 2003)
where they set the weights using the data of several
real integration cases. Of course, some of the prob-
lems of this approach are that it can only be used in
very static context and that the process of tuning the
parameters can be very expensive or require the sam-
pling of many scenarios in order to have a reliable
estimation.
There are works that use different similarity mea-
sures as features of a sample so that they can em-
ploy toolbox Machine Learning Algorithms. For ex-
ample (Wang et al., 2006) uses Support Vector Ma-
chine (SVM) as the classification model. The train-
ing is achieved by creating a set of matched instance
pairs with positive labels and a set of non-matched in-
stance pairs with negative labels. A binary classifier
is trained by using different similarity measurements
as features from the two pair sets. The classifier then
acts as a pairing function taking a pair of instances
(a, b) as input and generating decision values as out-
put. Since from a Kernel Theory point of view this
is equivalent to modifying the spectrum of the Gram
matrix by replacing each of the eigenvalues with its
square, our approach captures this kind of proposal.
(Ehrig et al., 2005) uses different machine learn-
ing techniques for classification (e.g. decision tree
learner, neural networks, support vector machines)
to assign an optimal internal weighting and thresh-
old scheme for each of the different feature/similarity
combinations of a given pair of ontologies. The
machine learning methods like C4.5 capture rel-
evance values for feature/similarity combinations.
To obtain the training data, they employ an exist-
ing parametrization as input to the Parameterizable
Alignment Method to create the initial alignments for
the two ontologies. The user then validates the initial
alignments and thus generates correct training data.
Some systems define a hierarchy of similarity
measures that are combined through a preestablished
process. This approach allows the systems to define
different types of mapping in which the kind of fea-
tures that are analyzed changes. A system of this kind
is HMatch (Castano et al., 2005) that defines four
matching models. The idea is that each model re-
flects different levels of complexity within the match-
ing process. To combine the different similarities,
it defines weights according to the characteristics of
each feature. For example, each semantic relation has
associated a weight W
sr
which shows the strength of
the connection expressed by the relation on the in-
volved concepts.
(Marie and Gal, 2008) proposes creating an en-
semble matcher by treating each similarity matrix
M(S, S
0
) as a weak classifier and finding a strong clas-
sifier using a modified version of Adaboost. They use
a compound measure formed by Precision and Recall
as the error function for each iteration. The principles
behind kernel theory and boosting are different mak-
ing it possible to complement this proposal with our
ideas.
(Duchateau et al., 2008) introduces the notion of
planning to the problem of similarity measure aggre-
gation. Although this is a very interesting idea and
we believe it can be used to extent most of the current
approaches, the solution currently requires the user
to manually create or modify a decision tree. This
heavily depends on the user, who does not necessarily
know exactly how the similarity measures should be
parametrized and aggregated.
Some works propose different operators to com-
bine different similarity measures. For example,
(M. Nagy, 2010), based on Dempster Schafer The-
ory of Evidence (Diaconis, 1978), proposes using
the Demspter Combination Rule m
i j
(A) = m
i
⊕ m
j
=
∑
m
i
(E
k
) ∗ m
j
(E
k
), where m
i
, m
j
are similarity mea-
sures and E
k
is the similarity value for a candidate
correspondence. Another similar approach is found
in (Ji et al., 2008) where they define what is called the
Ordered Weighted Average (OWA) operator and use
the linguistic quantifiers developed by Yager (Yager,
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
312

1988).
Finally, it is worth mentioning works that attempt
to formalize the combination task. For example,
(Stahl, 2005) investigates aspects of these approaches
in order to support a more goal-directed selection as
well as initiating the development of new techniques.
The investigation is based on a formal generalization
of the classic CBR cycle, which allows a more suit-
able analysis of the requirements, goals, assumptions,
and restrictions relevant in learning similarity mea-
sures. To simplify the selection of accurate techniques
within a particular application as well as for creating
foundations for future investigations, the work pro-
poses different categories for each of the following
three dimensions of the task of combining similarity
measures:
• Semantic of Similarity Measures: Determining
the Most Useful Case, Ranking the Most Use-
ful Cases, Approximating the Utility of the Most
Useful Cases and Probabilistic Similarity Mea-
sures.
• Training Data: Relative Case Utility Feedback,
Absolute Utility Feedback, Absolute Case Utility
Feedback and Utility Feedback.
• Learning Techniques: Probabilistic Similarity
Models, Local Similarity Measures and Feature
Weights.
3 MKL FOR ONTOLOGY
MATCHING
We want to find an appropriate combination of simi-
larity measures for an instance matching task. Specif-
ically, our interests lie in learning a linear combina-
tion of N similarity measures with nonnegative coef-
ficients β
j
that minimizes some error criteria e within
a given dataset Ψ. The elements of such dataset
are equivalent and non equivalent correspondences
C ∈ (I
1
, I
2
), where I
1
and I
2
are two homogeneous in-
stance sets:
mine(
∑
β
j
S
j
(c), Ψ) (1)
β ≥ 0
S
i
∈ ( f
i
, p
i
, m
i
), i ∈ 1..N
We see each similarity measure as a 3-tuple
( f
i
, p
i
, m
i
): f
i
is the actual similarity function, p
i
a
specific value set of parameters for the function and
m
i
a possible mapping between the properties of the
instances. We note that according to this description
the same similarity function can be part of two differ-
ent similarity measures.
The advantage of incorporating the mapping be-
tween properties as an additional component of the
similarity measure is that this allows us to conduct
the instance matching process even though there is
neither an unique property mapping nor certainty con-
cerning the correct mapping at the end of the schema
matching problem. In this case, it is sufficient to view
the mappings as an additional variable during the se-
lection of the similarity measures and allow the algo-
rithm to select the mappings that provide better infor-
mation to accomplish the task.
Our interest extends only to finding equivalence
correspondences among homogeneous instance sets
in which their elements belong to equivalence classes.
For this reason, to find all the correspondences be-
tween all the instances of two ontologies, it would be
necessary to carry on a schema matching process and
then to transverse the instance tree of the two ontolo-
gies in post-order.
This condition leads us to suppose that the under-
lying similarity rules are globally shared by the in-
dividuals of the set. To see that, consider a set in
which all its instances have a natural key but they can
be members of the concept PERSON or the concept
CAR. In this case, the natural key for each class will
be obviously different as is the correct combination of
similarity measures. While a person should be iden-
tified by its social security number, a car should be
identified by its license plate number.
We argue that the problem in equation (1) can be
solved using the MKL problem. In the following sec-
tion we present the advantages of such algorithm and
describe how it can be used in the instance match-
ing context assuming all similarity measures are also
a kernel. Then, we explain how it is possible to learn a
kernel from a similarity measure so that the algorithm
can be correctly employed.
3.1 MKL as Similarity Measure
Aggregator
If we limit ourselves to kernel functions (Scholkopf
and Smola, 2001) as similarity measures, define the
set of candidate correspondences as the input space,
label 1 for equivalent correspondences and −1 for
non equivalent correspondences, the problem stated
in equation (1) is equivalent to the MKL problem
(Bach et al., 2004). Under this setting, (Bach et al.,
2004) showed that this problem can be solved by the
QCP problem of equation (2) whose basic idea is to
train a classifier that minimizes the error in the dataset
while also learns the optimal coefficients as part of the
optimization problem.
MULTIPLE KERNEL LEARNING FOR ONTOLOGY INSTANCE MATCHING
313

min
ξ,α
ξ − 21
T
α (2)
sub ject0 ≤ α ≤ C, α
T
y = 0
α
T
D(y)S
j
D(y)α ≤ tr
S
j
c
ξ
ξ ∈ ℜ, α ∈ ℜ
n
where D(y) is the diagonal matrix with diagonal
y - the labels -, 1 ∈ R
n
, the unit vector, and C
a positive constant. The coefficients β j are re-
covered as Lagrange multipliers for the constraints
α
T
D(y)S
j
D(y)α ≤ tr
S
j
c
ξ.
There are several advantages of using MKL within
the context of ontology matching:
First, MKL allows us to find a sparse and non-
sparse combination of similarity measures by us-
ing various combinations of 1-norms and 2-norms.
Primarily 1-norms algorithms form a sparse linear
combination that can be useful in parameter selec-
tion where few kernels - the ones with the correct
parametrization - encode most of the relevant infor-
mation. On the other hand, 2-norm algorithms find a
non-sparse combination that can be useful when fea-
tures encode orthogonal characterizations of a prob-
lem (Marius Kloft and Sonnenburg, 2008); in other
words, this may be used to combine complementary
similarity measures such as Knowledge, String, and
Structural based measures.
Second, there are very efficient methods to solve
large scale MKL problems with a large number of
kernels ((Rakotomamonjy et al., 2008), (Sonnenburg
et al., 2006)). In fact, experimental results show that
the available methods work for hundreds of thousands
of examples or hundreds of kernels to be combined
and that have been applied in demanding applications
such as medical data fusion (Yu et al., ). This is ex-
tremely useful within the present context in which
large and complex ontologies have started to be a con-
cern.
Third, MKL directly addresses the problem of
combining similarity measures by using such com-
bination during the learning process. This is con-
trary to what happens when a neural network or any
other classic machine learning algorithm uses similar-
ity measures as features. Feature comparison and not
instance comparison is being carried out under this
condition, thus, the problem of instance matching is
not being directly addressed.
Fourth, a sparse and linear combination of simi-
larities such as the one producing MKL is simple and
easy to interpret. If a given situation is observed, all
a human has to do is analyze the larger and non zero
terms to understand which similarities are important
to classify a pair of instances, as different or equiva-
lent.
Finally, it is worthwhile mentioning that MKL is
an extension of the SVM algorithm that is capable of
learning from small training sets of high-dimensional
data with satisfactory precision (Wang et al., 2006).
3.2 Indefinite Kernels
Even though the configuration needed to use MKL
as a solver for (1) is simple and set forth a typical
scenario of binary classification, until now kernels
have been considered as similarity measures. How-
ever, most of the current similarity measures for on-
tology matching are not explicitly presented as a Ker-
nel. Furthermore, for most of the similarity functions
the question on whether or not these are kernels has
not even been raised.
On the one hand, kernels are very convenient func-
tions from an optimization point of view. The PSD
condition on the Gram matrix makes most of re-
lated optimization problems convex, and as a result,
low cost computation algorithms for solving them -
such as interior-point methods (Boyd and Vanden-
berghe, 2004) - become available. The related prob-
lems would be nonlinear without this condition, and
under the current technology, intractable.
Moreover, kernels have generalization advantages
over regular similarity functions. The latter imply
a significant deterioration in the learning guarantee.
(Srebro, 2008) found that if an input distribution can
be separated, in the sense of a kernel, with a margin γ
and an error rate ε
0
, then for any ε
1
> 0, this may also
be separated by the kernel mapping viewed as a sim-
ilarity measure, with similarity-based margin ε
0
and
error rate ε
0
+ ε
1
. Because ε
0
and ε
1
do not take neg-
ative values, a kernel-based margin is never smaller
than a similarity-based margin.
On the other hand, kernels also come with com-
promise and trade-offs. Their mathematical expres-
sions do not necessarily correspond to the intuition of
a good kernel as a good similarity measure and the
underlying margin in the implicit space is not usually
apparent in natural representations of the data (Balcan
and Blum, 2006). Therefore, it may be difficult for a
domain expert to use the theory to design an appro-
priate kernel for the learning task at hand. Further-
more, the requirement of positive semi-definiteness
may rule out most of the natural pairwise similarity
functions for the given problem domain.
To use MKL in the context of ontology match-
ing without losing the designability and interpretabil-
ity of similarity functions, we suggest following the
approaches that focus on finding a surrogate kernel
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
314

matrix K derived from the original similarity matrix S
(Wu et al., 2005).
To this regard, one of the first approaches was to
consider all the negative eigenvalues as noise and ap-
ply the linear transformation (3) to the similarity ma-
trix to replace all the eigenvalues with zero.
A
clip
= U
T
a
clip
U (3)
where a
clip
= diag(I
λ
1
>0
, ., ., ., ., I
λ
N
>0
).
Another common approach consists in changing
the signs of all negative eigenvalues - instead of mak-
ing them zero - by using the following linear transfor-
mation:
A
f lip
= U
T
a
f lip
U (4)
where a
f lip
= diag(sign
λ
1
>0
, ., ., ., ., sign
λ
N
>0
).
What we propose is to use the optimization prob-
lem stated in (Chen et al., 2009) to alter the original
similarity measure. This approach guarantees a con-
sistent treatment of all the samples because the same
linear transformation that is applied to the original
similarity matrix i.e. the one that creates the original
measure, can be applied to the new samples. Besides,
by controlling a parameter γ the user can control how
far to extend the search for the surrogate matrix.
The problem is presented in equation (5). Given
a similarity matrix S
m
calculated from a similar-
ity measure S and whose eigendescomposition is
UΛU
T
, this problem finds a linear transformation
A = Udiag(a)U
T
that modifies the original similar-
ity matrix by solving a small QCP problem that can
be handled by standard optimization packages:
min
c,b,ξ,a
1
n
1
T
ξ + ηc
T
K
a
c + γh(a) (5)
sub ject to diag(y)(K
a
c + b1) ≥ 1 − ξ
ξ ≥ 0, Λa ≥ 0
where h(a) is a convex function that regularizes the
search of the modified similarity matrix toward S
m
;
for example, one can use h(a) = ka − a
clip
k to fo-
cus the search at the vicinity of the A
clip
transforma-
tion. Since there may be different regularizers, we
suggest employing several of these to find surrogate
matrices and allow MKL to select the proper one. In
other words, the regularization function and the pa-
rameter coeficient may be seen as other components
of the similarity measure.
3.3 Putting the Ideas Together...
The following algorithm shows the suggested se-
quence to compose MKL and IK. There are three
steps in the process. The first one calculates differ-
ent transformations of similarity measures that use the
same similarity function. The second one uses MKL
with 1-norm to find a sparse combination of kernels
for each similarity function. The last one calls 2-norm
MKL to find a linear combination of similarity mea-
sures that analyzes different types of features.
Input: similarity measures, learning parameters
Begin:
//Step 1: Learn IK
for each similarityMeasure
for each regularizers and learningParameter
learnedKernel = learn2IndefiniteK (S, R, LP);
add (S, learnedKernel, ikList);
end;
end;
//Step 2: Call MKL with 1-Norm
for each similarityMeasure
ikList = getLearnedKernel(similarityMeasure);
sparseKernel = mklCombination(ikList, N1);
add (sparseKernel, sparseKList);
end;
//Step 3: Call MKL with 2-Norm
combination = mklCombination (sparseKList, N2);
End
Output: combination of orthogonal kernels.
3.4 Labeling and Unbalanced Classes
Because MKL is a supervised learning algorithm, an
oracle that labels a small set of candidate correspon-
dences as positive is required. The negative labels
can be constructed by crossing an instance of a posi-
tive correspondence with a random instance that is not
within the set given by the oracle. Depending on the
real application, the oracle can be a human or some
other system that does not require labels to accom-
plish the alignment. In this case, what could be of
value of our approach is the generalization capability
of a supervised learning paradigm.
On the other hand, the unbalanced nature of our
input space needs to be considered. An element of
our space is a candidate correspondence (I
i
, I
j
), where
I
i
, I
j
are instances of the sets to be matched. Conse-
quently, the cardinality of the input space is N × M,
where N and M correspond to the size of each of the
sets to be mapped. Within this setting, there will be
at most max(N, M) positive correspondences making
the rest negative.
This is a typical scenario of unbalanced classes
that can be treated with Cost-Sensitive or Sampling
Techniques. For example, it is possible to choose
the undersampling method which changes the train-
ing sets by sampling a smaller majority training set
(Drummond and Holte, 2003). As the performance of
every unbalance technique is highly dependent on the
data set (McCarthy et al., 2005), we suggest selecting
the technique by using cross validation.
MULTIPLE KERNEL LEARNING FOR ONTOLOGY INSTANCE MATCHING
315

4 EXPERIMENTS
A prototype in Java as a proof of concept was imple-
mented. Its architecture is depicted by figure 1.
We used the MKL implementation of Shogun
(Sonnenburg and Raetsch, 2010), and Mosek (Mos,
2010) to solve the QCP problem of equation (5).
The employed libraries of similarity measures were
(Chapman, 2009) for String measures and the Java
WordNet Similarity library for Knowledge based
measures. Jena OWL was the API to read the OWL
ontologies and the alignment files. We also incorpo-
rated a TSVM classifier as a final matcher ( module
8 in figure 1) whose training algorithm was imple-
mented by (Joachims, 2002).
Figure 1: Architecture of the Prototype.
4.1 Kernels and Similarity Measures
A composite kernel to compare two correspondences
C
i
,C
j
was used:
K(C
i
,C
j
) = K
internal
(C
i
)K
internal
(C
j
). (6)
where K
internal
refers to a kernel that measures the
similarities between the instances I
1
, I
2
of each can-
didate correspondence. Considering that the product
of two numbers is greater when they are close to each
other, this kernel takes greater values when the two
correspondences share a similar estimation of simi-
larity.
Two type of measures were employed as internal
kernels K
internal
:
The first one was the function K
internal
(I
1
, I
2
) =
P
m
i, j
(I
1
, I
2
) where m
i, j
is a specific alignment between
two properties lists of each ontology given by the
mapping m
i
and P is a local similarity function that
compares how similar the values of the two properties
of the two instances are. The idea behind this kernel
is to follow a natural key approach where the identity
of the instances is captured within the value of a few
properties.
The second internal kernel was an adapted ver-
sion of the tree-like function described in (Xue et al.,
2009) that is not stated as a Kernel. This measure
aims to find structural and semantic similarity. Its ba-
sic principle is to find how far apart two instance trees
are by computing the operations needed to transform
one tree into another. Since both functions require
to measure similarity between the values of the prop-
erties, the following list of local similarity functions
was used:
• String based: BlockDistance, ChapmanLength-
Deviation, CosineSimilarity, DiceSimilarity, Eu-
clideanDistance, JaccardSimilarity, JaroWinkler,
Levenshtein, MatchingCoefficient, MongeElkan,
SmithWatermanGotoh.
• Knowledge based: Lin, Resnik, Path, WuAnd-
Palmer.
Clearly, the fact that these similarity measures
were employed at the local level makes most of our
kernels indefinite.
4.2 Test Set and Results
We used the IIMB bechmark (Ferrara et al., 2008) as
basis for our preliminary experiments. The IIMB is
an evaluation dataset for the OAEI conference track
which consists of several transformations to a ref-
erence ontology. This ontology contains 5 named
classes, 4 object properties, 13 datatype properties
and 302 individuals. We make clear that we have not
participated in the official campaign.
There are a total of 37 matching tasks in the
benchmark. Each one introduces a class of modifi-
cations over the original value/s of a specific property
within the source ontology. For example, there are ty-
pographical error simulations, changes in the aggre-
gation level, and instantiation on different subclasses
of the same individual. Only the first 19 match-
ing tasks were tested because similarity measures de-
signed to capture logic heterogeneity were not em-
ployed.
The standard set of parameters for Ontology
Matching was used as evaluation measures:
• Precision: the number of correct retrieved map-
pings / the number of retrieved mappings.
• Recall. the number of correct retrieved mappings
/ the number of expected mappings.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
316

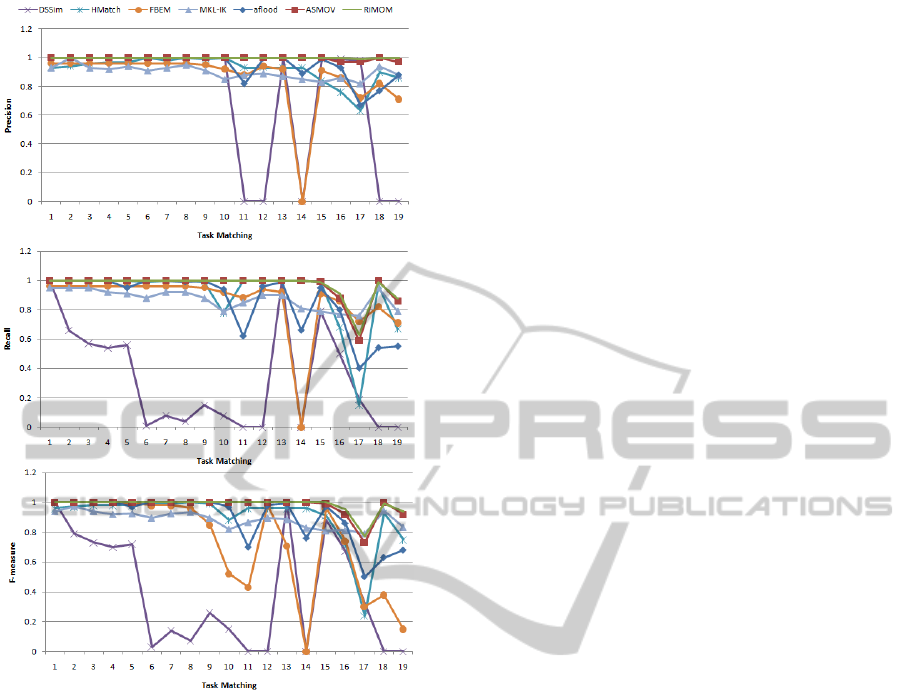
Figure 2: Protoype Behavior vs Other Systems.
• F-measure. 2 x (precision x recall) / (precision +
recall).
The following figures reveal the results of the pro-
totype (MKL-IK) and the systems that participated in
the OAEI 2009 (Euzenat et al., 2009).
Our prototype was comparable to the other tools in
the selected matching tasks. Besides, although most
of the time it was overcome by another system, it
showed a consistent behavior across every data set.
Both facts leads us to believe that the suggested ap-
proach should be further explored.
5 CONCLUSIONS AND FUTURE
WORK
In the present paper, we proposed to use Multiple Ker-
nel Learning (MKL) to combine similarity measures
within the context of Ontology Instance Matching.
We described the advantages of MKL and explained
how it can be used to address the problem. The need
to find surrogate similarity matrices to be able to use
such algorithm within this context, has been explained
and a possible approach to accomplish the task sub-
mitted. This approach consists in computing a linear
transformation that searches for the surrogate matrix
within the vicinity of the original similarity matrix.
We also suggested an algorithm that makes use of
both concepts and pointed how the unbalanced class
issues of the suggested configuration can be faced. In
addition, we implemented a proof of concept proto-
type and partially tested it using the IIMB benchmark.
The results suggest that our approach is feasible and
should be explored to extent current matching solu-
tions or to create new ones.
Our current research follows different directions.
We are particularly studying the internal behavior of
the algorithm and conducting a profound assessment
of the prototype through the use of other bechmarks
and test dataset. Furthermore, we are analyzing possi-
ble performance issues that may appear with this ap-
proach.
REFERENCES
(2010). The mosek optimization software.
Bach, F. R., Lanckriet, G. R. G., and Jordan, M. I. (2004).
Multiple kernel learning, conic duality, and the smo
algorithm. In ICML ’04: Proceedings of the twenty-
first international conference on Machine learning,
page 6, New York, NY, USA. ACM.
Balcan, M.-F. and Blum, A. (2006). On a theory of learn-
ing with similarity functions. In ICML ’06: Proceed-
ings of the 23rd international conference on Machine
learning, pages 73–80, New York, NY, USA. ACM.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press, New York, NY,
USA.
Castano, S., Ferrara, A., and Montanelli, S. (2003). H-
match: an algorithm for dynamically matching on-
tologies in peer-based systems. In Proc. of the 1st
VLDB Int. Workshop on Semantic Web and Databases
(SWDB 2003), Berlin, Germany.
Castano, S., Ferrara, A., and Montanelli, S. (2005). Match-
ing ontologies in open networked systems: Tech-
niques and applications. Journal on Data Semantics,
V.
Chapman, S. (2009). Simmetrics.
Chen, Y., Gupta, M. R., and Recht, B. (2009). Learning
kernels from indefinite similarities. In ICML ’09: Pro-
ceedings of the 26th Annual International Conference
on Machine Learning, pages 145–152, New York, NY,
USA. ACM.
Diaconis, P. (1978). [a mathematical theory of evidence.
(glenn shafer)]. Journal of the American Statistical
Association, 73(363):677–678.
MULTIPLE KERNEL LEARNING FOR ONTOLOGY INSTANCE MATCHING
317

Drummond, C. and Holte, R. C. (2003). C4.5, class imbal-
ance, and cost sensitivity: Why under-sampling beats
over-sampling. pages 1–8.
Duchateau, F., Bellahsene, Z., and Coletta, R. (2008).
A flexible approach for planning schema match-
ing algorithms. In OTM ’08: Proceedings of the
OTM 2008 Confederated International Conferences,
CoopIS, DOA, GADA, IS, and ODBASE 2008., pages
249–264, Berlin, Heidelberg. Springer-Verlag.
Ehrig, M., Staab, S., and Sure, Y. (2005). Bootstrapping on-
tology alignment methods with apfel. In WWW ’05:
Special interest tracks and posters of the 14th inter-
national conference on World Wide Web, pages 1148–
1149, New York, NY, USA. ACM.
Euzenat, J., Ferrara, A., Hollink, L., Isaac, A., Joslyn,
C., Malais
´
e, V., Meilicke, C., Nikolov, A., Pane, J.,
Sabou, M., Scharffe, F., Shvaiko, P., Spiliopoulos, V.,
Stuckenschmidt, H., Sv
´
ab-Zamazal, O., Sv
´
atek, V.,
dos Santos, C. T., Vouros, G. A., and Wang, S. (2009).
Results of the ontology alignment evaluation initiative
2009. In OM.
Euzenat, J. and Shvaiko, P. (2007). Ontology matching.
Springer-Verlag, Heidelberg (DE).
Ferrara, A., Lorusso, D., Montanelli, S., and Varese, G.
(2008). Towards a benchmark for instance match-
ing. In Shvaiko, P., Euzenat, J., Giunchiglia, F., and
Stuckenschmidt, H., editors, Ontology Matching (OM
2008), volume 431 of CEUR Workshop Proceedings.
CEUR-WS.org.
Ji, Q., Haase, P., and Qi, G. (2008). G.: Combination of
similarity measures in ontology matching using the
owa operator. In In: Proceedings of the 12th Inter-
national Conference on Information Processing and
Management of Uncertainty in Knowledge-Base Sys-
tems.
Joachims, T. (2002). SVM light.
Kalfoglou, Y. and Schorlemmer, M. (2005). Ontology map-
ping: The state of the art. In Semantic Interoperability
and Integration, Dagstuhl Seminar Proceedings. Inter-
nationales Begegnungs- und Forschungszentrum f
¨
ur
Informatik (IBFI).
Laub, J., Macke, J., Muller, K.-R., and Wichmann, F. A.
(2007). Inducing metric violations in human similar-
ity judgements. In Advances in Neural Information
Processing Systems 19, pages 777–784. MIT Press,
Cambridge, MA.
M. Nagy, M. V.-V. (2010). [towards an automatic semantic
data integration: Multi-agent framework approach].
Marie, A. and Gal, A. (2008). Boosting schema match-
ers. In OTM ’08: Proceedings of the OTM 2008 Con-
federated International Conferences, CoopIS, DOA,
GADA, IS, and ODBASE 2008., pages 283–300,
Berlin, Heidelberg. Springer-Verlag.
Marius Kloft, Ulf Brefeld, P. L. and Sonnenburg, S. (2008).
Non-sparse multiple kernel learning.
McCarthy, K., Zabar, B., and Weiss, G. (2005). Does cost-
sensitive learning beat sampling for classifying rare
classes? In UBDM ’05: Proceedings of the 1st in-
ternational workshop on Utility-based data mining,
pages 69–77, New York, NY, USA. ACM.
Rakotomamonjy, A., Bach, F., Canu, S., and Grandvalet, Y.
(2008). SimpleMKL. Journal of Machine Learning
Research, 9.
Scholkopf, B. and Smola, A. J. (2001). Learning with Ker-
nels: Support Vector Machines, Regularization, Opti-
mization, and Beyond. MIT Press, Cambridge, MA,
USA.
Shvaiko, P. and Euzenat, J. (2008). Ten challenges for ontol-
ogy matching. In On the Move to Meaningful Internet
Systems: OTM 2008, volume 5332 of Lecture Notes
in Computer Science, chapter 18, pages 1164–1182.
Berlin, Heidelberg.
Shvaiko, P. and Shvaiko, P. (2005). A survey of schema-
based matching approaches. Journal on Data Seman-
tics, 4:146–171.
Sonnenburg, S. and Raetsch, G. (2010). Shogun.
Sonnenburg, S., R
¨
atsch, G., Sch
¨
afer, C., and Sch
¨
olkopf, B.
(2006). Large scale multiple kernel learning. J. Mach.
Learn. Res., 7:1531–1565.
Srebro, N. (2008). How good is a kernel when used as a
similarity measure?
Stahl, A. (2005). Learning similarity measures: A for-
mal view based on a generalized cbr model. In Op-
tional Comment/Qualification: Validation of Inter-
Enterprise Management Framework (Trial 2), pages
507–521. Springer.
Wang, C., Lu, J., and Zhang, G. (2006). Integration of on-
tology data through learning instance matching. In WI
’06: Proceedings of the 2006 IEEE/WIC/ACM Inter-
national Conference on Web Intelligence, pages 536–
539, Washington, DC, USA. IEEE Computer Society.
Wu, G., Chang, E. Y., and Zhang, Z. (2005). An analysis
of transformation on non-positive semidefinite simi-
larity matrix for kernel machines. In Proceedings of
the 22nd International Conference on Machine Learn-
ing.
Xue, Y., Wang, C., Ghenniwa, H., and Shen, W. (2009). A
tree similarity measuring method and its application
to ontology comparison. j-jucs, 15(9):1766–1781.
Yager, R. R. (1988). On ordered weighted averaging ag-
gregation operators in multicriteria decisionmaking.
IEEE Trans. Syst. Man Cybern., 18(1):183–190.
Yu, S., Falck, T., Daemen, A., Tranchevent, L.-C., Suykens,
J. A. K., De Moor, B., and Moreau, Y.
KEOD 2010 - International Conference on Knowledge Engineering and Ontology Development
318