Automatic Feature Selection for Operational Scenarios

of Satellite Image Understanding using Measures

of Mutual Information

Dragos Bratasanu

, Ion Nedelcu

and Mihai Datcu

Romanian Space Agency ROSA, Mendeleev 21-25, 010362, Bucharest, Romania

DLR German Aerospace Center, Oberpfaffenhoffen D-82234 Wessling, Germany

Abstract. The Earth Observation processing tools operating in the recent scena-

rio need to be tailored to the new products offered by the sub-meter spatial reso-

lution imaging sensors. The new methods should provide the image analysts the

essential automatic support to discover relevant information and identify signif-

icant elements in the image. We advocate an automatic technique to select the

optimum number features used in classification, object detection and analysis of

optical satellite images. Using measures of mutual information between the tar-

get classes and the available features, we investigate the criterions of maxi-

mum-relevance and maximum-relevance-minimumredundancy for automatic

feature selection at very-low cost. Following a comprehensive set of experi-

ments on multiple sensors, applications and classifiers, the results demonstrate

the possible operational use of the method in future scenarios of human-

machine interactions in support of Earth Observation technologies.

1 Introduction

The methods and ways users operate the Earth Observation (EO) satellite data in the

present scenario are beginning to change the paradigms of classical image analysis. If

in the past the existent automatic classification and segmentation tools provided good

results for mapping of decameters resolution images, nowadays these tools fail to

offer the users the necessary support in discovering relevant information in the image.

The old methods for knowledge-based image understanding were operating on

two distinct levels: pixel level (e.g. classification techniques in which each pixel is

assigned with a label) and region level (e.g. segmentation techniques in which homo-

geneous image regions are assigned with labels). The resolution of new optical sen-

sors has reached values of centimeters (e.g. GeoEye-1 0.41m, Quickbird 0.6m and

World-View-2 0.50m) and outran the capabilities of standard information mining tools

to infer knowledge using spectral and spatial information. Future tools need to look at

the way analysts understand the data and how the current manual operations are per-

formed. We introduce an approach based on patch-level analysis, capturing contextual

information – sub-meter resolution image areas interconnect complex structures cov-

ering many pixels with high diversity of spectral information. By using this approach

we line up to the way users create cartographic products for multiple applications (e.g.

Bratasanu D., Nedelcu I. and Datcu M..

Automatic Feature Selection for Operational Scenarios of Satellite Image Understanding using Measures of Mutual Information.

DOI: 10.5220/0003143101090117

In Proceedings of the International Workshop on Semantic Sensor Web (SSW-2010), pages 109-117

ISBN: 978-989-8425-33-1

 2010 SCITEPRESS (Science and Technology Publications, Lda.)

maps for emergency response, geo-intelligence, forensics). Maybe the most important

step in all automated procedures is to identify the optimum set of attributes – feature

selection - to minimize the classification error. Using the minimum-redundancy-

maximum-relevance (mRMR) criterion [1] based on mutual information, we intro-

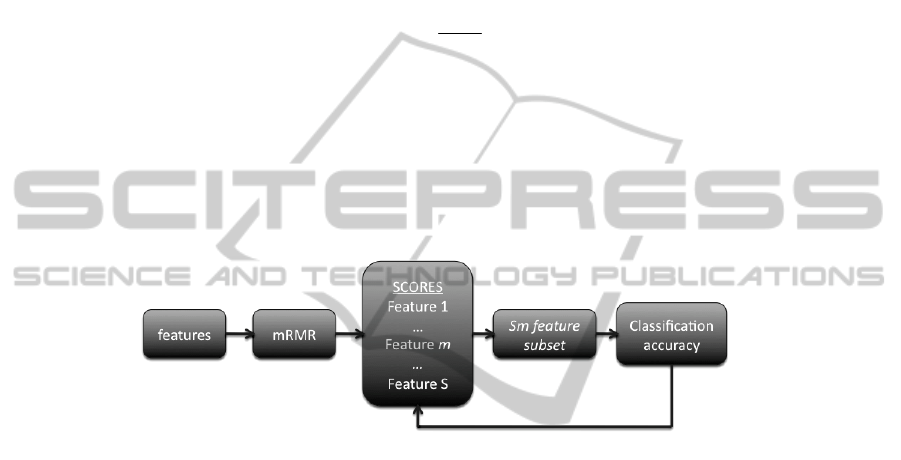
duce a method to select an ideal set of features from the available set. Fig.1 shows the

workflow of our procedure.

Fig. 1. Workflow for selecting the optimum features for target class classification.

We test the resulting attributes using four classifiers (Minimum Distance, Maximum

Likelihood, Mahalanobis Distance and Latent Dirichlet Allocation (LDA) [2]). The

minimum of the classification error yields the optimum feature set as a function of the

operating classifier. The results confirm that the mRMR method applied to sub-meter

resolution data improves classification accuracy for applications based on the new

sensors.

2 Theoretical Approaches

2.1 Feature Selection using Statistical Measures of Mutual Information

In all information-mining applications, feature selection (characterizing attributes for

a given class) is a critical step in minimizing the classification error. Having available

a data set D described by M features

{, 1... }

xi M==

and the target class C, the

problem is to discover a subspace of m features

in the feature space

that cha-

racterizes C. Of course, the score for each possible feature set needs to be related to

an operational classification algorithm. The question that rises is ‘what subset

RRÌ

is the optimum for the problem at hands?’ Since there are countless combi-

nations of the existent attributes, we use an incremental method explained in the fol-

lowing paragraphs.

The optimal characterization condition most of the times implies minimal classifi-

cation error for the target class, which in turn requires the maximal statistical depen-

dency of the target class C on the data distribution in the subspace

. In literature,

this condition is known as maximal dependency.

The maximal dependency approach is widely debated in information theory publi-

cations and the most familiar way to obtain it is to use maximum relevance (MR)

criterion – selecting the features m with the highest relevance to the target class C.

The relevance of features

to the features in C is defined in terms of mutual infor-

mation. Given two random variables x and y with probability density functions p(x)

and p(y), the following formula gives their measure of mutual information:

110

(, )

(, ) (, )log

() ()

pxy

xy pxy dxdy

pxpy

òò

(1)

The selected features

need to yield the largest mutual information

(,)

IxC

with the target class C. In the incremental search, the first m maximum scores of mu-

tual information

(,)

IxC

yield the selection of the best m features.

The MR criterion gives a good start in the feature selection problem but it does not

answer two critical questions: ‘what is the optimum number of features m to select

from the mutual-information

(,)

IxC

scores’ and ‘are all these selected attributes

useful to minimize the classification error?’ In information theory it is widely ac-

cepted that the combination of individually good features may lead to confusion in

classification results if they have a high level of mutual redundancy. One approach to

reduce redundancy amongst characteristics is the minimum redundancy (mR) crite-

rion.

In [3] the authors introduce a minimum-redundancy-maximal-relevance (mRMR)

framework to select the optimum number of features and minimize redundancy

amongst them. We will describe this method in the following paragraphs.

2.2 Category Discovery using Maximum relevance Minimum Redundancy

When considering mutual information the reasoning for discovering the optimum set

of attributes, the goal is to find a feature set S with m features

{}

, which jointly

have the largest dependency, on the target class C (2).

( , ) max( ( , 1... ), )

axDependency S C I x i m C==

(2)

Because maximum dependency is often hard to implement even for discrete ran-

dom variables, maximum relevance criterion (MR) has been proposed as alternative

in publications. The MR criterion approximates the dependency between multiple

random variables by selecting the features approximating

max( ( , 1... ), )

Ixi m C=

with the mean value of all mutual information values be-

tween individual features

and class C (3).

max ( , ) max ( , )

xx S

DSC I x C

(3)

It is well known in remote sensing literature that usually features (e.g. spectral bands)

may present high redundancy for a specific target class. When two or more variables

have a rich content of mutual information, discriminating between the target class and

the rest does not change if one feature is removed. In order to select mutually exclu-

sive features, the criterion of minimum redundancy (mR) may be used following the

MR. (4)

min( ,( )) min ( , )

xx S

RS Ixx

æö

èø

(4)

111

The criterion that combines the MR and the mR is called minimum-redundancy-max-

relevance (mRMR) [3]. We choose the form (5) to combine the above formulas,

where D is the max-relevance and R is the min-redundancy:

max( )mRMR D R=-

(5)

In operational application we used an incremental version for selecting the feature set.

If we have m-1 selected attributes, the task is to select the m-th feature that maximizes

the mRMR condition (6):

max ( , ) ( , )

jji

xXS

Ix C Ix x

Î-

(6)

2.3 Choosing the Optimal Feature Set

After determining the score for each feature with the mRMR tests, the remaining

issue is to determine the optimum number of attributes m. To discover the feature set

SSÌ

we follow the workflow in figure 2.

Fig. 2. Selecting the optimum feature set.

The process of selecting the optimum characteristics for a specific target class in-

cludes the following steps:

1. Determine the available features for the satellite image – spectral bands, textural

information, etc

2. Choose a patch from the image representing the target class

3. Determine the score of the mRMR tests for each feature

4. Begin with the top 3 features

S3 and determine the classification accuracy for each

adjacent features sets

S3 ⊂ S4 ⊂ S5...⊂ Sm. The feature set that yields the low-

est classification error

min( )

ee=

gets selected to be the optimum one.

2.4 Multiple Classifiers

The mRMR feature selection scheme does not imply the use of a specific classifier.

We have tested this approach on multiple supervised classifiers with the same train-

ing set and discovered that optimum attributes differ not only with respect to the tar-

get class but also with respect to the operational classifier. We used in our case stu-

112

dies the Minimum Distance, Mahalanobis Distance, Maximum Likelihood and Latent

Dirichlet Allocation described in [2].

The Minimum Distance classifier discovers the classes of interest by the following

rules [4]. Suppose

are the means for the M classes determined from the training

data and x is the position of the pixel to be classified. Classification is performed on

the basis of:

xwÎ

(, ) (, )

dxm dxm<

for all

ji¹

(7)

Maximum Likelihood classification works on the following principles [4]. Let the

spectral classes for an image be represented by

,1...

iMw =

with M the total number

of classes. A pixel x is assigned to class

if:

(|) ( |)

pxp xww>

for all

ji¹

(8)

(|) (|)()/()

iji

pxp xp pxwww=

(9)

P(ωi)istheaprioriprobabilityofclass

tooccurintheimage.

The Mahalanobis Distance classifier assigns each pixel in the image to one of the

training classes based on the following distance measure [4]:

(, ) ( ) ( )

ii i

dxm x m x m

=- -

(10)

The Latent Dirichlet Allocation based classifier is thoroughly described in [2] and

works by assigning each pixel and each patch in the image to a specific ‘latent’ topic

generated from the training patches. For all classifiers, experiments and results are

presented in the following section.

3 Operational Case Studies and Results

3.1 Urban Areas Extraction using WorldView-2 Satellite Image

In the first case study we aim to discover the optimum feature set and extract the

urban areas from a WorldView-2 image (resolution of 0.5 meters / pixel). Figure 3

shows the test image and the training patch used to indicate the target class.

113

Fig. 3. WorldView-2 image and the target class Urban areas.

The first set of features contained only the 8 spectral bands provided by the sensor

(costal, blue, green, yellow, red, red-edge, nir-1, nir-2). We computed the MR and

mRMR values between all features in the data set and the target class and drew the

score table as shown in figure 4.

Fig. 4. The scores for the features in the data set and the results of mRMR criterion.

After evaluating the mRMR scores, we train the test classifiers with patches

representing the target class and classes labeled as ‘others’. The first three top features

(nir-1, blue, yellow) are tested first and then each feature in the scores table in added

to the classifier. Figure 5 shows how each classifier operates better on a different set

of input features, yielding different accuracy values (the y-axis) as function of the

input features (the x-axis). The Maximum Likelihood classifier gives the best accura-

cy value (93%) with the first three features (nir-1, blue, yellow) and the target class

mask is shown in figure 6.

Fig. 5. Classification accuracy as a function of the input features and the classifier used.

114

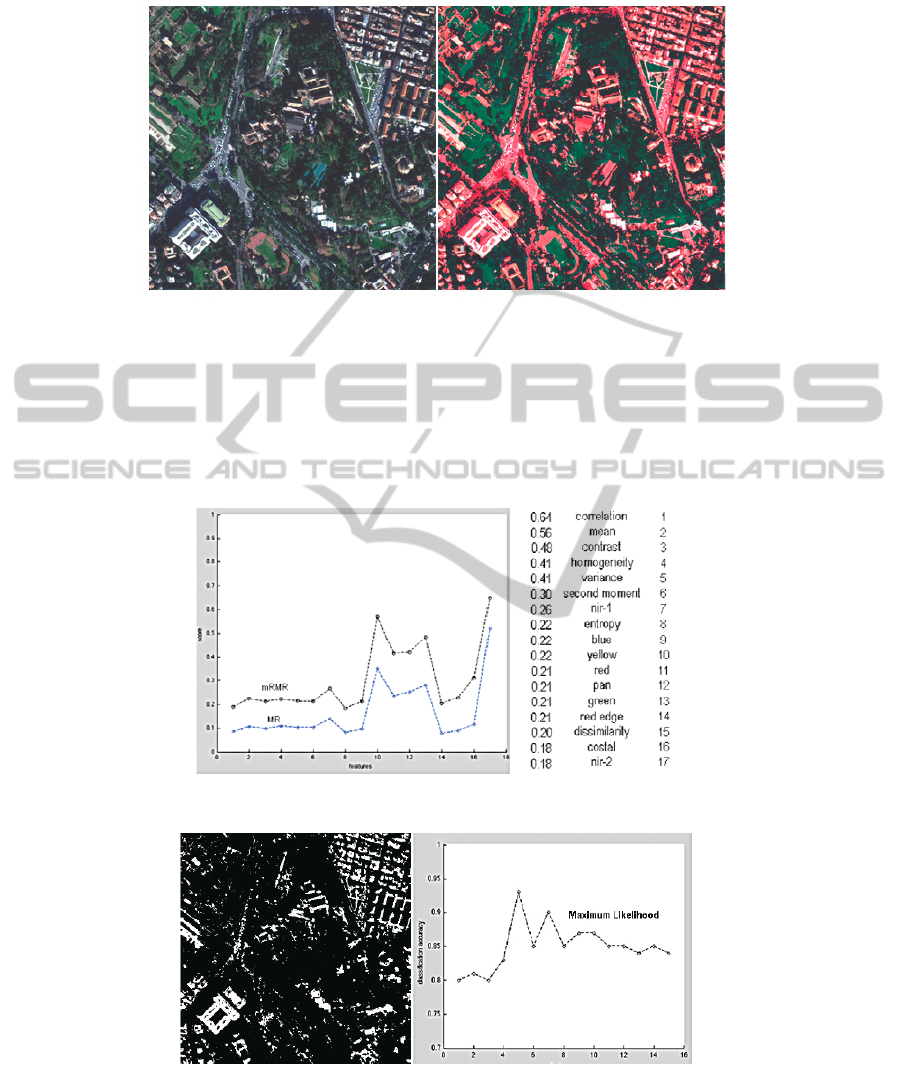
Fig. 6. WorldView-2 image and the target class extracted with Max Likelihood.

We added textural information to the first set of features and recomputed the MR and

mRMR values between all features in the data set and the target class. The table score

is presented in figure 7. We compute the classification accuracy for the first three top

features and then add an extra attribute each step and re-perform the experiments.

From the graphics in figure 8 we can easily understand that the best accuracy is ob-

tained by using the first 7 features in the score table with Maximum Likelihood.

Fig. 7. MR and mRMR scores for the features in test.

Fig. 8. Target class and the classification accuracy as a function of the features in test.

115

3.2 Urban Areas Extraction using GeoEye-1 Satellite Data

In the second case study we aim to discover the optimum feature set and extract the

urban areas from a Geoeye-1 image (resolution of 0.41 meters / pixel). Figure 9

shows the test image and the training patch used to indicate the target class.

Fig. 9. GeoEye-1 image and the target class Urban areas.

On this image we performed three types of experiments, with different input feature

sets. The first set consists only of spectral information, the second contains the spec-

tral bands and textural information and the third has the spectral bands and the vegeta-

tion index NDVI. Each experiment gave different scores for the mRMR tests and the

top is presented in figure 10. Figure 11 shows the classification accuracy of the target

class as function of the input features and the classifier used. The graphics show that

the lowest error is obtained by the Minimum Distance classifier applied to the first

four textural features in the score table.

Fig. 10. mRMR score for three different feature sets of GeoEye-1 image.

4 The Sensor Data-knowledge Continuum

The recent and future scenarios of sensorics arise with the promise of new capabilities

for collecting and distributing information about the world. However, there is still a

gap between the raw data coming from the sensor in form of numbers (measures of

116

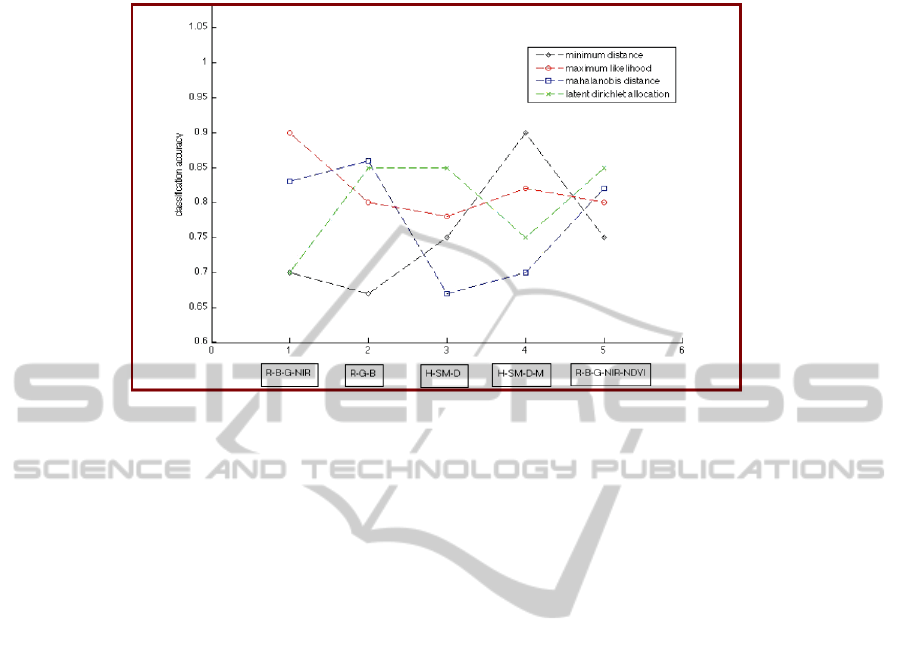
Fig. 11. Classification accuracy scores for GeoEye-1 image, target class Urban areas.

physical phenomena) and applied user-oriented knowledge (in form of meaning).

When the human mind understands an object or an event, it classifies it automati-

cally into an acknowledged category with sense and implicit semantic denotation.

We introduce a procedure to describe an important layer of automatic data

processing i.e. feature selection with the aim of supporting the users to find what they

are looking for in the collection of data. In order to add human-oriented conceptual

meaning to the abstract representation of sensor information, semantics may be intro-

duced at different steps of the workflow.

The mRMR technique yields highly accurate results when used with a layered

classifier – inferring classes one at a time. The user indicates the target category; adds

a descriptive caption to it and detects the optimum features simultaneously. This ap-

proach ensures that the class of interest is extracted with maximum accuracy and in

the same time it is represented in the concepts domain by the wording chosen by the

user. Thus, the added semantics provide an inter-connection between layers of infor-

mation in the sensor data-knowledge continuum.

References

1. Peng, H., Long, F., Ding, C.: Feature Selection Based on Mutual Information: Criteria of

Max-Dependency, Max-Relevance and Min-Redundancy. IEEE Transactions on Pattern

Analysis and Machine Intelligence. Vol. 27. No.8. 2005. Pp 1226-1238

2. Bratasanu, D., Nedelcu, I., Datcu, M.: Bridging the gap for satellite image annotation and

automatic mapping applications. IEEE Journal of Selected Topics in Applied Earth Obser-

vations and Remote Sensing, accepted paper 2010

3. Ding, C., Peng, H.: Minimum Redundancy Feature Selection from Microarray Gene Ex-

pression Data. Proc. Second IEEE Computational Systems Bioinformatics Conference.

2003. Pp 523-528

4. Richards, J., Jia, X.: Remote Sensing Digital Image Analysis. 4th Edition. Springer, 2006.

117