
A NOVEL COMBINED NETWORK TRAFFIC PREDICTION
MODEL IN COGNITIVE NETWORKS
Xiaopu Shang
1
, Xiaomin Zhu
2
1
Institute of Information Systems, Beijing Jiaotong University, Beijing, China
2
School of Mechanical, Beijing Jiaotong University, Beijing, China
Dandan Li
Institute of Information Systems, Beijing Jiaotong University, Beijing, China
Keywords: Cognitive network, Traffic prediction, Neural network, Wavelet, Auto-regression.
Abstract: With the development of the network technology, the concept of Cognitive Network has been proposed and
studied, and various kinds of algorithms and models in Cognitive Networks thus have become an hot topic
of research. This paper proposes a novel model, which includes three stages. The proposed model may
achieve a high-precision traffic prediction in cognitive networks. The model solves some problems in
cognitive networks, such as low adaptive capability and an easy trap in local optimum when coming up with
a fluctuated network flow.
1 INTRODUCTION
The structure of Next Generation Network (NGN) is
becoming complicated and heterogeneous, while
Cognitive Network (CN) (Thomas R W, 2005) is
justly adaptive to the NGN because it has the ability
of autonomous learning and reconfiguration. A CN
can provide, over an extended period of time, better
end-to-end performance than a non cognitive
network. Cognition could be used to improve
resource management, Quality of Service (QoS),
security, access control, or many other network
goals.
In the research area of CN, the design of a
multi-time scale network traffic predication model
with “congnition” will play a key role in the
cognitive performance of the entire network and in
the load-balancing and traffic scheduling algorithm
of the congnitive network. According to the result of
traffic prediction, the CN can allocate the network
resource in advance, make data flow distributes
reasonably in the net, cope with load fluctuation,
reduce network congestion.
In the research of network traffic prediction
model, there are two difficulties (Kasabov N, 2002):
(1) A large scale network contains many complex
nonlinear systems, meanwhile it works under
some periodic fluctuations and trends of
nonlinear rising and falling.
(2) Computer network is subjected to interferences
of many random factors, but traditional single
models have poor adaptive capacity. So we
need combination models to realize traffic
prediction.
We analyze the present situation of network
traffic prediction, improve the wavelet pretreatment
method and BPNN(BP Neural Network) method,
design a network prediction model using combined
NN(Neural Network), and we simulate our model in
the environment of MATLAB to verify and analyze
the model. The conclusion proves the new model
work more precisely than traditional model.
The remainder of this paper is organized as
follows. Section 2 introduces the present research of
network traffic prediction. Section 3 accordingly
describes the related theories of this new model.
Section 4 presents the combination schemes and the
three-stage prediction model. The simulate results of
this new model are presented and analyzed in
section 5. Finally, section 6 makes an overall
conclusion.
205
Li D., Zhu X. and Shang X.
A NOVEL COMBINED NETWORK TRAFFIC PREDICTION MODEL IN COGNITIVE NETWORKS.
DOI: 10.5220/0003268502050211
In Proceedings of the Twelfth International Conference on Informatics and Semiotics in Organisations (ICISO 2010), page
ISBN: 978-989-8425-26-3
Copyright
c
2010 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 A BRIEF REVIEW OF
NETWORK TRAFFIC
PREDICTION
The conception of CN is developed on the basis of
cognitive radios, and current researches mainly
focus on link layer, so research in network traffic
prediction of CN is not enough. However,
fundamentally the algorism of traffic prediction in
CN is to show “cognition”, provide necessary data to
other elements of CN. Thus, from the aspect of time
and data, it demands higher efficiency and precision
than traditional model.
The present technologies of network traffic
prediction can be divided into linear prediction and
nonlinear prediction. ARIMA model (Feng Huifang,
2005) and Kalman Filter model are the examples of
linear prediction model, such as self-adaptive linear
model proposed by Lv Jun (2004). As the linear
model can hardly describe the true features of real
network traffic, nonlinear prediction models are
proposed by scholars. Of course, nonlinear models
sometimes may include linear elements, such as
multi-scale combination predication model proposed
by Khotanzad A (2003). In these kind models, as
nonlinear elements play a more important role than
linear elements, we still call them nonlinear model.
The typical model of nonlinear model is NN model.
The predication model based on NN can be
divided into two kinds. One is to put some algorithm
inside NN, form the scheme as Figure 1 shows.
Figure1: The forcasting model of algorithm inside NN.
WNN (Wavelet Neural Network) proposed by Wang
Peng (2008) just put wavelet decomposition
algorithm into hidden layer of NN. We call this
Prediction Model of NN with Build-in Algorithm.
The other is to separate the data processing and
onefold NN’s prediction as figure 2.
Figure 2: The forecasting model of algorithm outside NN.
The data pre-processing provides data more
suitable to the input of NN, we call this Prediction
Model of NN with Outside Algorithm. One such
combined NN model is presented by (Feng Hailiang,
2006). This is the main form nowadays. The model
we designed is just based on this.
Considering the character of nonlinear and
multi-scale in network traffic, Lei Ting (2006) gives
the resolution. They demonstrate the traffic and then
forecast the irregular part with ENN. Combine with
linear NN and nonlinear NN, a model that optimize
the forecasting result 4 times is proposed by Feng
Hailiang (2006), the precision is improved, but the
time it needs is not short enough. As for the
traditional problem in prediction model proposed by
Kasabov N (2002), some scholars, such as Wang
Peng (2008) and Cheng Guang (2004) have formed
all kinds of improved models based on NN,. Also,
traditional NN models have the problem of lagging
in learning and are easy to trap in local optimum,
owning limited ability in coping with sudden load in
the net. In order to solve this problem, the main
resolution is put wavelet decomposition algorithm
inside the 3rd layer of BPNN, Han Zhijie (2008)
properly deals with the local suboptimal, but still
spends much time getting a satisfying result.
Combine wavelet decomposition with NN as
prediction model is also a main resolution (Feng
Hailiang, 2006), but after the wavelet
decomposition, only a single kind of NN still have
the problem of rap into local optimum and cannot
develop the advance of multi-scale analysis of
wavelet.
3 RELATED THEORIES
3.1 Wavelet Transform
If square integrable function ψ(t) ε L2(R) meet the
following condition:
21
|()|||d
ψω ω ω
∧
+∞
−
−∞
<+∞
∫
, or
() 0tdt
ψ
+∞
−∞
=
∫
Where Ψ^(ω) is the Fourier
transform of Ψ(ω), than call it mother wavelet.
Through stretching and translation transformation,
the mother wavelet can be changed into wavelet
function:
ψa,b(t)= ψ(at-b),b ε R-{0}
(1)
In our model, we use the form of discrete
wavelet transformation as follows:
ICISO 2010 - International Conference on Informatics and Semiotics in Organisations
206

2
,
() , 2 ( (2 ))
j
j
jjk
D
kf f xkdx
ψψ
+∞
−
−
−∞
≤≥ −
∫
(2)
Where j is frequency domain resolution and k is
time shifting amount. Then we do expansion on time
series.
{f(t), t=1,2,…} is traffic time series, wavelet
function and scaling function can be described as:
1, 1 1,
() () () () ()
jjk j jk
k
f
tAktDkt
φψ
+∞ +∞
−−−
=−∞ −∞
=+
∑∑
(3)
Where
2
,
() 2 (2 )
j
j
jk
ttk
φφ
−
−
=−
and
2
,
() 2 (2 )
j
j
jk
ttk
φψ
−
−
=−
are scale space orthogonal basis and wavelet space
orthogonal basis separately, Aj(k) and Dj(k) are
scale coefficient and wavelet coefficient separately.
1,
() ()
φ
+∞
−
=−∞
∑
jjk
k
A
kt is the part of high frequency in
signal which shows detail signal and usually
contains noisy. And
11,
() ()
ψ
+∞
−−
−∞
∑
jjk
Dk t is the part
of low frequency in signal, it reflects the nature
character of signal, such as the trend of a signal or
the signal period.
As for this thesis, we demonstrate the traffic with
Mallat Algorithm, the algorithm can realize the
demonstrate simply and rapidly, and we have no
need to know the concrete structure of wavelet
function, wavelet decomposition or reconstruction
can be done with just a set of filter coefficients.
0
1
2
11
1
2
11
() ()
( ) 2 [ (2 ) (2 1)], 1,2,...,
() 2 [ (2) (2 1)]
jjj
jjj
Ak fk
A
kAkAkj L
Dk D k D k
−
++
−
++
=
=++=
=++
(4)
L is the number of layer, Aj(k) is approximation
signal, and Dj(k) is the detailed signal.
3.2 Auto-regression Model
Auto-regression (AR) model is a time series model.
Let {X
t
} denote time series, it is the linear function
of prophase expectation and stochastic component:
11 2 2tt t ptpt
XX XLX
φ
φφε
−− −
=+ ++ +
(5)
Where
1
φ
,
2
φ
,L,
p
φ
are autoregressive
coefficients, we use Levinson-Durbin recursive
algorithm (
Burg J P, 1975) to get their specific value.
Stochastic component
t
ε
, is a white noise series,
and it obeys standard normal distribution.
As for this thesis, we use AR model to forecast
the low frequency data that meet the stationary
condition, this may improve the forecasting speed
and promote forecasting efficiency.
3.3 Neural Network Model
Nowadays, BPNN, ENN, HNN, and KNN, etc. are
the popular NN models in use. We just introduce
KNN and BPNN that we used in the novel model.
KNN’s main idea is to self organize the
information outside into a conception in brain. As
for a system, it is just to organize a corresponding
presentation format in system automatically when
affected by information outside the system. This
includes adjustment of the NN’s weight coefficient.
KNN is a typical self organizing neural network
which is also called SOM. Its input layer is
monolayer and single-dimensional neurons, while
the output layer is two-dimensional neurons. The
format of lateral interaction between neurons in
output layer is Mexican Cap. So in the output layer,
KNN has the feedback character that the neurons are
closer, the effect is stronger. Thus, KNN can be the
detector of mode characteristics and an effective
method to enhance the ability of self adaptivity. In
this view, KNN can be a prompt model in the use of
network traffic prediction.
Based on the original NN, through self-organized
learning to simulate the biological nerve reflex is the
typical character of KNN. In a complex nonlinear
system that changes greatly, KNN can improve the
forecasting precision by the change of the content
and amount of study.
The learning process of KNN is as follows:
(1) Initialize the link weights, each weight can be
initialized from the training data arbitrarily;
(2) X
k
=
(
x
1
,x
2
,…,x
n
)
is input vector, for each input
vector, calculate the Euclidean distance W
ij
which
between X
i
k
and all of the output node N
j
;
(3) N
j*
, which has the minimum distance in
output node, is the winner in competition:
*
{1,2,..., }
min { }
jj
jm
dd
∈
=
;
(4) Adjust the link weights between output node
N
j*
and every input node X
i
k
in geometric
neighborhood: w
i j
=w
i j
+ η(t) (x
i
k
– w
ij
),
i∈{1, 2, ..., n },where η(t) is learning rate: 0<η(t)<1
;
(5) As for different t: t=1,2,…, come back to step
(3).
BPNN is a multilayer feed forward network
based on error back-propagation algorithm, which is
one of the broadly used ANN models. BPNN can
learn and restore many input-output mapping
relations without mathematical equations that reveal
A NOVEL COMBINED NETWORK TRAFFIC PREDICTION MODEL IN COGNITIVE NETWORKS
207

the relation between them. The learning rule of
BPNN is to make use of the steepest descent
method, continuously adjust the net weights value
and net threshould value by back propagation in
order to get a minimum square sum of error. The
learning course of BPNN is as figure 3.
As the one of the basic ANN model, BPNN
works on the principle of continuous error feedback:
The error is transmitted through output layer, then to
the hidden layer and input layer, and weight in every
layer can be corrected in the method of gradient
descent algorithm. In cycles of information forward
propagation and error back propagation, weights in
every layer can be modified, and this is the process
of NN’s learning. This process will last until the
output error can be accepted or the set learning times
are met.
Figure 3: The learning course of BPNN.
4 A NOVEL THREE-STAGE
COMBINED NETWORK
TRAFFIC PREDICTION
MODEL
4.1 Basic Thinking of the New Model
The network traffic is generally a kind of
non-stationary time series signal. The non-stationary
of traffic increased the difficulty of prediction, thus
we shall consider the preprocessing of the traffic
signal, so as to achieve relative stationary in-put
signals in the prediction of our model. The
technology of wavelet decomposition (Ardagna C A,
2008) is the best solution. Wavelet decomposition
can decompose non-stationary time series into
several detailed signals and a more stationary signal
via low-pass filter. After decomposition, the traffic
is more unitary in frequency, and thus help improve
the prediction of the model.
AR model has a good performance in the
prediction of relative stationary traffic, and it can
reduce the prediction time and improve the
efficiency of the whole forecasting model.
KNN model can keep the character of wavelet’s
multi-scale analysis, avoid poor adaptive ability of
wavelet coefficient in processing, achieve the aim of
dynamic learning while reduce the NN’s learning
period, avoid being trapped in local optimum, thus
improve the performance of prediction model.
According to Kolmogorov Theory, if the number
of input unit is N, then the unit number of hidden
layer is always 2N+1. In this model, we use the
superposition of traffics which predicted by AR and
KNN model as the input of BPNN. For BPNN’s
excellent ability of function approximation, we can
get a more accurate forecasting result with small
error.
4.2 Describe in Detail of the Novel
Model
Based on the analysis above, we form the structure
of the new model as Figure 4.
Figure 4: Three-stage combined NN model in CN.
In the first stage of the model, decompose the
nonlinear traffic signal with Mallat algorithm
according to formula (4).
In the second stage, in line with formula (5),
forecast the relatively stationary signal by AR
model; as for the nonlinear and non-stationary high
frequency signal, we use KNN model to make the
forecasting. In the last stage, BPNN fit the
superposition of former forecasting results, output a
high precision final result.
Compared with the traditional single NN model, this
model avoid the problem of trapping in local
optimum. And compared with ENN model proposed
by Wang Peng (2008) and put wavelet
ICISO 2010 - International Conference on Informatics and Semiotics in Organisations
208

decomposition inside the hidden layer of BPNN, the
new model resolve the problem of long learning
period and poor self-adaptivity under a sudden load.
Figure 7: Wavelet decomposition of network traffic.
The speed of wavelet decomposition and linear
forecasting can make up the delay of NN’s learning,
improve the efficiency of the whole model. In reality
application, regular learning cycle can be written
into protocol and save the net resource in CN. As a
NN with good output performance, BPNN makes
the forecasting result more accurate. Also, its ability
in learning can make up the defect of long time
learning and poor self-regulation mentioned above.
Meanwhile, as a non-stationary model, BPNN is
suitable to depict the non-stationary traffic.
Because this novel model can reduce the
forecasting time, improve the forecasting precision,
and receive a result with high precision under wide
traffic fluctuation. So in the aspect of time and
precision, this new model shows the meaning of
cognition. It can work in the net under the condition
of multi-background traffic or multi-scale time
variation, provide a timely, accurate, steady
cognitive platform to the high level algorithms in
CN.
5 SIMULATION AND ANALYSIS
We simulate in the environment of MATLAB (Liu
Linhui, 2008). MATLAB is an advanced computing
language and interactive environment which is
widely used in algorithm development, data
visualization, data analysis and data computing.
As figure 5 shows, we collect the network traffic
from a core router in the backbone network. The
sampling interval is an hour, we gathered 900
samples, each sample is the average traffic value in
an hour, and the last 100 samples have been used to
test the forecasting result. Figure 6 is the curve line
of traffic.
Figure 5: Collection of network traffic data.
Figure 6: Curve line of network traffic.
For the traffic above, according formula (4), use
Mallat algorithm to decompose it. In order to
improve the precision without loss of generality, we
A NOVEL COMBINED NETWORK TRAFFIC PREDICTION MODEL IN COGNITIVE NETWORKS
209
set scale coefficient L=5. Thus we can get series{
D1(k), D2(k), D3(k), D4(k), D5(k), A5(k)} after
wavelet decomposition, the original signal
S=d1+d2+d3+d4+d5+a5. The result of wavelet
decomposition is as figure 7.
Then we input the low frequency a5 into AR
model to forecast. At the same time, normalize the
high frequency d1, d2, d3, d4, d5, and input them
into KNN to forecast. The weight values and
threshold values of KNN are determined by
self-learning. We set the start learning rate on 0.95,
the minimum learning rate on 0.001, the maximum
step of training on 5000. At last, composite the AR
model’s forecasting result and KNN model’s
forecasting result, make it as the input of BPNN.
According the Kolmogorov algorithm mentioned
above, there are 3 hidden layers in BPNN.
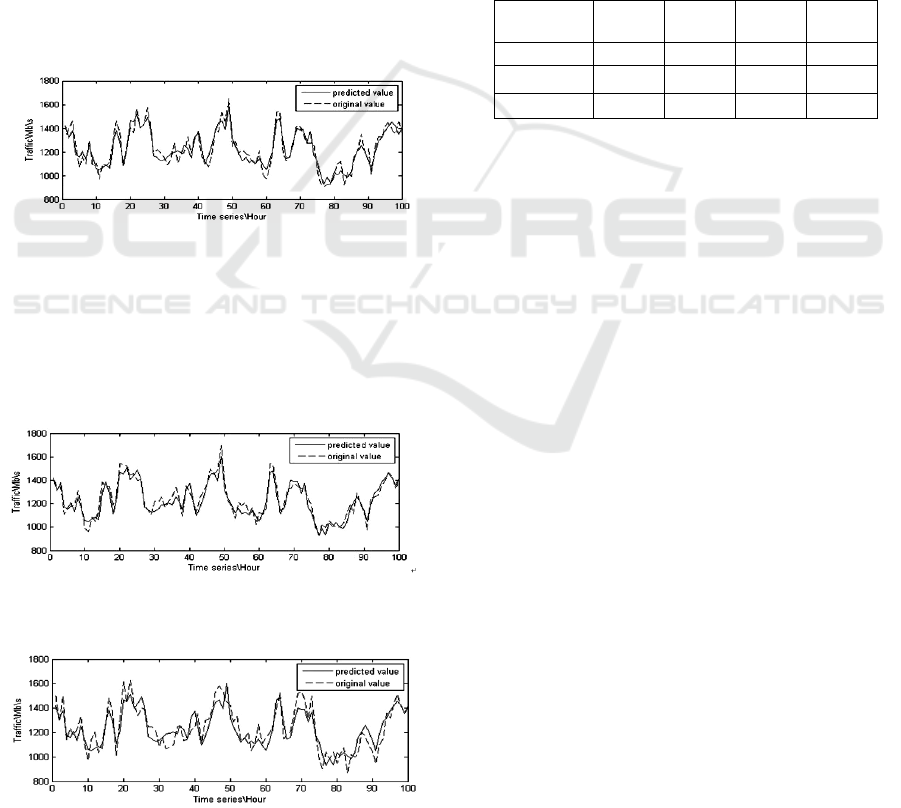
Figure 8 is one-step forecasting result of the 100
data samples, and we compare the real traffic with
the prediction result in one Figure.
Figure 8: One-step forecasting result compared with real
traffic.
Figure 9 is the comparison of two-step
forecasting result and the real traffic. And figure 10
is the forecasting result of WNN model which has
put wavelet decomposition into BPNN as described
earlier in the thesis.
Figure 9: Two-step forecasting result compared with real
traffic.
Figure 10: WNN forecasting result compared with real
traffic.
By the contrast of forecasting result and real
traffic, and the contrast of new model and WNN
model, the simulation proves the high precision of
the novel model. And we have expatiated earlier the
advantage of efficiency and time cost of this model.
Some data of the model’s performance are listed
in Table 1. We make a contrast between statistic
data of one-step, two-step forecasting result and the
statistic data of WNN model. In table 1, SSE means
Squared Sum Error, MSE means Mean Squared
Error, MAE means Mean Absolute Error and MRE
means Mean Relative Error.
Table 1: Comparison of forecasting performance.
Method
SSE
%
MSE
%
MAE
%
MRE
%
WNN 10.79 1.84 7.60 21.17
One-step 5.12 0.98 4.50 16.02
Two-step 7.01 1.38 5.04 18.98
6 CONCLUSIONS
Taking into account the multi-scale and non-linear
characters of the network traffic, combined with the
wavelet decomposition, AR model and NN models,
the thesis proposes a novel network forecasting
model that suitable in CN. The main idea of the
model are as follows: In stage one, the traffic signal
is decomposed into low-frequency part and
high-frequency part. In stage two, two kinds of the
signals are predicted with AR model and KNN
model respectively. To enhance the prediction
accuracy and merge the traffic characters captured
by individual models, the output of the previous
models are combined using BPNN. At the end of the
thesis, the simulation and comparison suggest that
the proposed model has better performance than
WNN model, and may achieve a high-precision
traffic prediction result, thus can work satisfactorily
in the use of CN.
REFERENCES
Thomas R W, DaSilva L. A, MacKenzie A B. 2005. New
frontiers in dynamic spectrum access networks. 2005
First IEEE International Symposium: 352 – 360
Kasabov N. 2002. DENFIS: Dynamic evolving
neural-fuzzy inference system and its application for
ICISO 2010 - International Conference on Informatics and Semiotics in Organisations
210

time-series prediction. Fuzzy System, IEEE
Transactions: 144 – 154
Feng Huifang, Shu Yantai. 2005. Study on network traffic
prediction techniques. Wireless Communications,
Networking and Mobile Computing: 1041-1044
Lv Jun, Li Xing, Congsen Ran, He Tao. 2004. Network
traffic prediction and fault detection based on adaptive
linear model. IEEE ICIT International Conference.
Volume 2: 880 – 885
Khotanzad A, Sadek N. 2003. Multi-scale high-speed
network traffic prediction using combination of neural
networks. Neural Networks, Proceedings of the
International Joint Conference. Volume 2: 1071-1075
Wang Peng, Liu Yuan. 2008. Network traffic prediction
based on improved BP wavelet neural network.
Wireless Communications, Networking and Mobile
Computing: 1-5
Feng Hailiang, Chen Di, Lin Qingjia, Chen Chunxiao.
2006. Multi-scale network traffic prediction using a
two-stage neural network. WiCOM International
Conference: 1 - 5
Lei Ting, Yu Zhengwei. 2006. A wavelet neural network
model of network traffic forecast. Journal of
Computer Application, Volume (3): 526-528 (in
Chinese)
Cheng Guang, Gong Jian, Ding Wei. 2004.
Nonlinear-periodical network traffic behavioral
forecast based on seasonal neural network model.
2004 Communications, Circuits and Systems: 683-687
Han Zhijie, Wang Ruchuan. 2008. Novel peer to peer
network traffic prediction algorithm. Computer
Science, Volume(9): 40-41 (in Chinese)
Feng Hailiang, Chen Di, Lin Qingjia, Chen Chunxiao.
2006. Combined prediction model of Internet traffic
based on neural network. Journal of Computer
Application, Volume (9): 108-111 (in Chinese)
Burg J P. 1975. Maximum entropy spectral analysis. US:
Stanford University.
Ardagna C A, Bernardoni E, Damiani E, Reale S. 2008.
Mobile network traffic data compression by means of
wavelet decomposition. Second IEEE International
Conference on Digital Ecosystems and Technologies :
274-280
Liu Linhui, Chen Jie, Xu Lixin. 2008. Realization and
application research of BP neural network based on
MATLAB. Future BioMedical Information
Engineering International Seminar: 130 – 133
A NOVEL COMBINED NETWORK TRAFFIC PREDICTION MODEL IN COGNITIVE NETWORKS
211
