MODELING CELL PROLIFERATION ACTIVITY OF HUMAN

INTERLEUKIN-3 UPON SINGLE RESIDUE REPLACEMENTS

Majid Masso and Iosif I. Vaisman

Department of Bioinformatics and Computational Biology, George Mason University

10900 University Blvd. MS 5B3, Manassas, Virginia, U.S.A.

Keywords: Delaunay tessellation, Statistical potential, Computational mutagenesis, Structure-function relationships,

Random forest supervised classification, Prediction.

Abstract: The signaling molecule human interleukin-3 (IL-3) is responsible for promoting the growth of a wide range

of hematopoietic cell lineages in the bone marrow. In this study, we apply an in silico mutagenesis

technique to investigate the effects of single amino acid substitutions in the IL-3 protein on cell proliferation

activity. The computational mutagenesis, which utilizes the IL-3 protein structure as well as a knowledge-

based, four-body statistical potential, empirically quantifies environmental perturbations at the mutated

residue position in IL-3 and at all neighboring positions in the folded structure. In particular, mutated

position perturbation scores alone are capable of characterizing IL-3 residues grouped by physicochemical,

functional, or structural properties. Additionally, these scores elucidate an IL-3 structure–function

relationship based on a collection of 630 single residue replacements for which activity changes were

experimentally measured. A random forest classifier trained on this dataset of experimental mutants, whose

respective feature vectors include environmental changes at the mutated position and at six nearest

neighbors in the IL-3 structure, achieves 80% accuracy and outperforms related state-of-the-art methods.

1 INTRODUCTION

Human interleukin-3 (IL-3) is a short-chain, bundled

four-helical cytokine that is produced primarily by

activated T-cells and acts in the bone marrow to

promote the growth of most precursor blood cell

lineages (Bagley et al., 1996, Feng et al., 1996,

Klein et al., 1997, Olins et al., 1995). It is a

relatively small signaling protein consisting of 133

amino acid residues (Figure 1A) that most closely

resembles granulocyte-macrophage colony

stimulating factor (GM-CSF) and IL-5, both of

which also possess four-helical bundles and belong

to the same family of short-chain cytokines (Bagley

et al., 1996, Feng et al., 1996). Unlike the other

members of this family, a short fifth α-helix is also

apparent in the IL-3 structure (Feng et al., 1996,

Klein et al., 1997). Cell proliferation activity is

initiated via the binding of IL-3 by a heterodimeric

IL-3Rα/Rβ transmembrane receptor on target cells

(Bagley et al., 1996, Klein et al., 1997). IL-3

specifically binds the Rα receptor subunit with low-

affinity, and it otherwise displays no affinity for the

Rβ chain; high-affinity IL-3 binding requires both

receptor subunits and the formation of an IL-3-IL-

3Rα/Rβ ternary complex (Bagley et al., 1996, Klein

et al., 1997). Signal transduction is subsequently

mediated by the Rβ receptor, whereby tyrosine

phosphorylation of the Rβ cytoplasmic domain by

JAK2 kinase is followed by induction of the STAT5

transcriptional pathway (Bagley et al., 1996, Feng et

al., 1996, Klein et al., 1997).

A solution structure has been determined for a

multiply substituted and truncated variant of human

IL-3 consisting of residue positions 14 – 125 (Feng

et al., 1996). The NMR coordinates, deposited into

the Protein Data Bank (PDB) under accession code

1jli (Berman et al., 2000), provide a minimized

average structure obtained from a family of 25

convergent structures with an average backbone

root-mean-square deviation of 0.88±0.15 angstroms

(Feng et al., 1996). Although a total of 14 residue

changes were introduced into the truncated protein

in order to make it sufficiently soluble and stable for

NMR studies, a cell proliferation assay revealed the

variant to be fully active (Feng et al., 1996).

Additionally, the results of saturation (Olins et al.,

1995) and site-directed (Bagley et al., 1996)

Masso M. and I. Vaisman I..

MODELING CELL PROLIFERATION ACTIVITY OF HUMAN INTERLEUKIN-3 UPON SINGLE RESIDUE REPLACEMENTS.

DOI: 10.5220/0003112700930101

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 93-101

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

mutagenesis experiments on IL-3 have been reported

in the literature, whereby cell proliferation assays

were used for measuring the activity associated with

a total of 630 single residue substitutions in the

native protein. The synthesized IL-3 mutants were

subsequently categorized based on their degree of

activity relative to that of the wild type protein.

In this study, we implement a computational

mutagenesis procedure for representing mutants of

human IL-3 due to single amino acid replacements.

The method utilizes a coarse-grained depiction of

protein structure as a collection of constituent amino

acid residue Cα coordinates in 3-dimensional (3D)

space. For each structure, the points serve as vertices

for a 3D tetrahedral tiling known as a Delaunay

tessellation (de Berg et al., 2008); hence, every

tetrahedron identifies a quadruplet of residues at the

vertices. Initially, a large and diverse set of protein

structures is tessellated, from which an amino acid

four-body potential is subsequently developed based

on statistical analysis of the residue quadruplets

collectively generated by the tetrahedra. Next, we

describe the in silico mutagenesis technique and how

its application to a protein such as IL-3 requires both

tessellation of its 3D structure and use of the four-

body statistical potential. For each single residue

replacement in IL-3, the method quantifies ensuing

environmental perturbations at the mutated position

and at structurally nearby positions that form a local

neighborhood as identified by the tessellated protein

structure. As will be shown in this manuscript, these

perturbation scores elucidate IL-3 structure-function

relationships and are valuable for developing a

predictive model of mutant IL-3 activity based on

implementation of a random forest classifier.

2 MATERIALS AND METHODS

2.1 Experimental Data

Theoretically, there are a total of 19 × 112 = 2128

possible single residue substitutions that can be

introduced into positions 14 – 125 of the available

human IL-3 structure. The principal dataset for this

study contains 630 of these IL-3 mutants,

representing amino acid replacements distributed

throughout the primary sequence of the protein at all

but 12 positions. Biological activity of these

experimentally synthesized IL-3 mutants was

determined via cell proliferation assays that

measured the incorporation of [

H] thymidine into

either AML193.1.3 (Olins et al., 1995) or TF-1

(Bagley et al., 1996) erythroleukemic cell lines.

Figure 1: (A) Ribbon diagram of human interleukin-3 (IL-

3) based on PDB accession code 1jli (Pettersen et al.,

2004). (B) Delaunay tessellation of IL-3 using Cα vertices

generates a convex hull of tetrahedral simplices

Mutant IL-3 activity was reported as a

percentage of the wild type (wt) protein,

summarized by the following categorical

distribution: 27 “increased activity” mutants (>

100% wt), 373 “full activity” mutants (20 – 100%

wt), 75 “moderate activity” mutants (5 – 19% wt),

and 155 “low activity” mutants (< 5% wt). As a two-

class system of IL-3 mutants, we consider the

following subsets: 400 that are “unaffected”

(“increased” and “full” combined) and 230 that are

“affected” (“moderate” and “low” combined) by

their respective residue substitutions.

2.2 Delaunay Tessellation and the

Four-Body Statistical Potential

The Delaunay tessellation of a set of points P = {x

, x

, …, x

} in 3D Euclidean space yields a convex

hull of space-filling, non-overlapping, irregular

tetrahedra whose combined vertices consist of

precisely all elements of P (Figure 1B). Two

adjacent tetrahedral simplices in a tessellation may

share a triangular face (three out of four points in

common), a linear edge (two points in common), or

a single vertex. Provided that no three points of P

are collinear, no four points are coplanar or on the

same circle, and no five points are on the same

sphere, there exists a unique Delaunay tessellation of

P (de Berg et al., 2008). The technique is applied to

a protein structure by initially abstracting to points

the constituent amino acids, which for this study are

selected to be the Cα atomic coordinates, to yield a

coarse-grained representation of the protein. Each of

the simplices in the ensuing protein structure

tessellation objectively identifies at the vertices a

quadruplet of structurally nearest neighbor amino

acid residues. To ensure only biochemically feasible

quadruplet interactions, all protein structure

tessellations are modified by the removal of edges

longer than 12 angstroms (Figure 2A). Delaunay

tessellation implementations and visualizations, and

all subsequent data analyses are performed using a

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

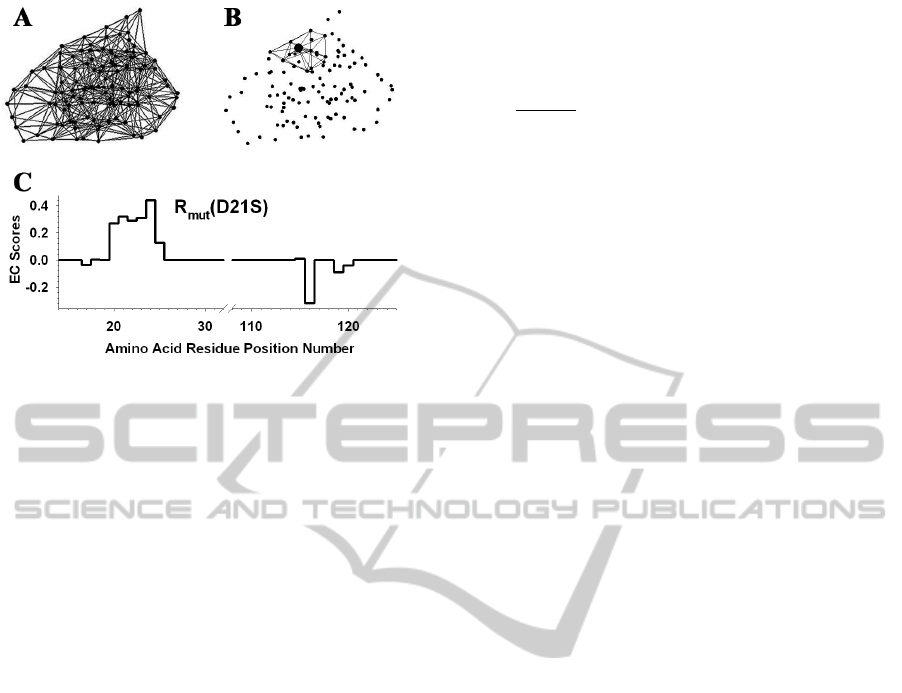
Figure 2: (A) Delaunay tessellation of IL-3 subject to an

edge length cutoff of 12 angstroms. (B) Subset of 14

tetrahedral simplices that share the Cα vertex of amino

acid residue D21 (enlarged relative to the others). There

are a total of 11 other vertices among these simplices, and

the residues they represent form the neighborhood of D21.

mut

vector for the D21S mutant of IL-3. The nonzero

EC value at position 21 is the residual score of the D21S

mutant, and the other 11 nonzero EC scores identify the

D21 neighborhood positions.

combination of Qhull (Barber et al., 1996), Matlab

(Version 7.0.1.24704 (R14) Service Pack 1), and an

ad hoc suite of Java and Perl codes.

The amino acid building blocks of proteins form

a K = 20 letter alphabet A. The number of r = 4 letter

subsets (quadruplets) of A that can be enumerated,

assuming permutations of four letters in a quadruplet

do not constitute new subsets but that a quadruplet

may contain repeats of the same letter, is given by

.8855

14201

⎟

⎠

⎞

⎜

⎝

⎛

−+

⎟

⎠

⎞

⎜

⎝

⎛

−+

These conditions reflect the facts that ordering is not

taken into account when four amino acids are

identified at the vertices of simplices in protein

structure tessellations, and that the same amino acid

may appear multiple times in a protein chain and in

structurally close proximity to form the vertices of a

simplex. Since on average only a few hundred

simplices and their respective quadruplets are

encountered when a single protein is tessellated, a

diverse dataset of 1417 high-resolution protein

structures with low sequence and structure similarity

was selected for tessellation using the PISCES

server (Wang and Dunbrack, 2003) in order to

reliably calculate simplicial nearest neighbor relative

frequencies of occurrence f

ijkl

for all 8855 possible

quadruplets (i, j, k, l) in protein structure space. A

rate expected by chance for the quadruplets is

obtained from the multinomial reference distribution

()

.4 and 1 where,

===

∑∑

∏

ijkl

taa

In the above formula, a

represents the proportion of

amino acids of type n in the 1417 tessellated protein

structures, and t

is the number of occurrences of

amino acid n in the quadruplet. Through an

application of the inverse Boltzmann principle from

statistical mechanics (Sippl, 1993), a knowledge

based statistical potential of quadruplet interaction is

given by the log-likelihood score s

ijkl

= log (f

ijkl

), and the collection of 8855 quadruplet types

together with their respective scores defines the

four-body statistical potential (Carter et al., 2001).

2.3 Computational Mutagenesis

With the Delaunay tessellation of the human IL-3

protein structure, the four-body statistical potential

can be used to assign a score to each of the

constituent tetrahedral simplices equivalent to that of

the amino acid quadruplet identified at its four

vertices. Since each amino acid vertex is generally

shared by a number of adjacent tetrahedral

simplices, the residue participates in multiple nearest

neighbor quadruplets. All amino acids represented at

the other vertices of these simplices collectively

form a neighborhood of that shared residue, and any

position in a protein structure tessellation rarely has

fewer than six neighbors (Figure 2B). Although

amino acids positions in the neighborhood are all

structurally near their shared residue in 3D

Euclidean space, they are often distant from the

shared residue in primary sequence. For an amino

acid at primary sequence position i in the protein,

the residue environment score q

is defined as the

sum of scores of all tetrahedral simplices that share

its Cα vertex (Carter et al., 2001, Zhang et al., 2008).

The environment scores of all amino acids in the

native protein can be arranged to form a 3D-1D

potential profile (Bowie et al., 1991) vector Q

, q

, …, q

>, where the translation i = i – 13

has been applied to the residue positions 14 – 125 of

the human IL-3 structure, and N = 112. A similar

profile Q

mut

can be obtained for any IL-3 mutant due

to a residue substitution at some position j, by first

replacing the identity of the amino acid accordingly

at the vertex representing position j in the

tessellation, and then recalculating all the residue

MODELING CELL PROLIFERATION ACTIVITY OF HUMAN INTERLEUKIN-3 UPON SINGLE RESIDUE

REPLACEMENTS

environment scores. However, the only environment

scores that are actually altered occur at the mutated

position j and at those that form its neighborhood in

the tessellation. The difference R

mut

= Q

mut

– Q

< EC

, EC

, …, EC

> is a sparse mutant vector

that quantifies relative environmental changes or

perturbations EC

= q

i,mut

– q

i,wt

at every residue

position i in the protein due to the mutation (Carter

et al., 2001, Zhang et al., 2008). Since the only

nonzero EC components of R

mut

occur at mutated

position j and at positions in its neighborhood,

important local effects of a mutation are effectively

modelled; however, long-range consequences at

structurally distant protein positions are excluded

(Figure 2C). We refer to the EC

component in the

vector R

mut

at the mutational epicenter j as the

mutant residual score, due to its significance as a

summary measure of the relative change in mutant

IL-3 sequence-structure compatibility from that of

the native protein. Finally, a comprehensive

mutational profile (CMP) for IL-3 is a vector

obtained by calculating at each position the mean of

residual scores associated with all 19 amino acid

replacements, where each component is a CMP

score for the corresponding position (Carter et al.,

2001, Zhang et al., 2008).

Conformational changes are effectively

accounted for by this computational mutagenesis,

both implicitly, through the four-body potential and

the perturbation vectors R

mut

, and explicitly, due to

the use of only coarse-grained Cα representations of

structures and the fact that Delaunay tessellations are

robust to small shifts in the Cα coordinates. Hence, a

solved structure for every human IL-3 mutant is not

required, and tessellation of the only available IL-3

structure suffices. Moreover, these conditions

suggest that despite the fact that this IL-3 structure

contains 14 residue changes, its tessellation can be

used to represent that of the wild type protein by

altering the identities of the amino acids at the

corresponding vertices to those found in the native

IL-3 protein. With these initial alterations, Q

can

then be computed for wild type IL-3, followed by

3D-1D potential profiles Q

mut

and perturbation

vectors R

mut

for all single residue mutants.

2.4 Random Forest Classification and

Evaluation of Performance

A feature vector is generated for each single point

human IL-3 mutant whose input attributes

(independent variables or predictors) include the

mutated position number, the identities of the native

and replacement amino acids at the mutated

position, the residual score (i.e., EC score at the

mutated position), and the EC scores at the six

nearest neighborhood positions ordered nearest to

farthest based on 3D Euclidean distance of each

neighbor from the mutated position. Next, we

include the ordered amino acid identities at the six

nearest neighbors as well as their ordered primary

sequence locations relative to the mutated position

(i.e., difference between neighbor and mutated

position numbers). Finally, the following input

attributes are added as feature vector components:

(1) The computed mean volume and mean

tetrahedrality for the set of Delaunay simplices that

utilize the mutated position as a vertex;

(2) The secondary structure {H, helix; C, coil} at

the mutated position;

(3) Depth {S, surface; U, undersurface; B, buried}

at the mutated position (tessellation-based surface

accessibility). Surface positions participate as one

of three vertices defining a triangular facet for

exactly one tetrahedron in the tessellation.

Undersurface positions are defined as non-surface

positions that share an edge with a surface

position. All other positions are buried;

(4) A count of the number of simplex edges the

mutated position shares with surface positions

(zero by definition for buried positions).

The mutant IL-3 activity class defines the output

attribute (dependent variable) associated with each

feature vector.

The supervised classification scheme that we

employ for this study is an implementation of Leo

Breiman’s random forest (RF) algorithm (Breiman,

2001), available as part of the WEKA suite of

machine learning tools (Frank et al., 2004). The RF

algorithm incorporates a bagging (bootstrap

aggregating) procedure to train an ensemble of

classification trees, and predictions are based on a

majority vote. The split at each node encountered in

the growing trees is based on a fixed-size random

subset of the predictor attributes. Also, though all

trees are unpruned, the algorithm does not overfit

regardless of the number of selected trees.

Generally, the RF algorithm performs better than

other supervised classification methods (Bordner,

2008, Qi et al., 2006). We fix the adjustable RF

parameters in this study at 100 trees, and 5 input

attributes are randomly selected for splitting at each

tree node.

RF performance on the dataset of IL-3 mutant

feature vectors is evaluated by using stratified

tenfold cross-validation (10 CV), leave-one-out

cross-validation (LOOCV), and stratified random

split (66% of dataset for model training and 34% for

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

testing). Given TP (TN) = total number of correctly

predicted “unaffected” or “U” (“affected” or “A”)

mutants and FN (FP) = total number of respectively

misclassified mutants, the overall accuracy is

defined as Q = (TP + TN) / (TP + FN + FP + TN).

For the “unaffected” class, S(U) = sensitivity = TP /

(TP + FN) and P(U) = precision = TP / (TP + FP),

while for the “affected” class, S(A) = TN / (TN +

FP) and P(A) = TN / (TN + FN). Finally, the

balanced error rate (BER) and balanced accuracy

rate (BAR), calculated as BER = 0.5 × [FN / (FN +

TP) + FP / (FP + TN)] and BAR = 1 – BER,

Matthew’s correlation coefficient (MCC), given by

FP)FN)(TNFP)(TNFN)(TP(TP

FNFP-TNTP

MCC

++++

××

and area (AUC) under the receiver operating

characteristic (ROC) curve provide alternative

measures that are especially useful for unbalanced

classes. A chi-square test can be applied to assess

MCC statistical significance, where the test statistic

is given by χ

= M × MCC

(M = number of

predictions) with one degree of freedom (Baldi et

al., 2000). An ROC curve is a plot of true positive

rate (sensitivity) versus false positive rate (1 –

specificity), and AUC is equivalent to the non-

parametric Wilcoxon-Mann-Whitney test of ranks

(Fawcett, 2003). An AUC value near 0.5 suggests

the trained model will not perform better than

random guessing, while a value of 1.0 indicates a

perfect classifier.

3 RESULTS AND DISCUSSION

3.1 Human IL-3 Structure-Function

Relationships

We begin by generating perturbation vectors R

mut

for all 2128 mutants of human IL-3 due to single

residue substitutions at positions 14 – 125, from

which residual scores are obtained for the 630

mutants of IL-3 with experimentally classified

activity. Next, a mean residual score is calculated for

the IL-3 mutants in each of the four activity

categories and reflects a clear trend (Figure 3A),

whereby increasingly detrimental effects on

structure (i.e., decreasing mean residual scores) are

associated with higher levels of functional

impairment (i.e., diminished levels of activity).

Moreover, based on six separate t-test applications, a

statistically significant difference exists between

Figure 3: Human IL-3 structure-function correlation based

on (A) four mutant activity categories and (B) two

functional classes (C / NC = conservative / non-

conservative amino acid substitutions).

mean residual scores associated with each pair of

activity classes in Figure 3A (p < 0.05 in all cases).

The mutants in each class of Figure 3A are

further categorized based on whether the residue

replacements are conservative (C) or non-

conservative (NC) relative to the native amino acids,

and mean residual scores are computed for each of

these subgroups. With the 20 amino acids clustered

into six groups as {(A,S,T,G,P), (D,E,N,Q),

(R,K,H), (F,Y,W), (V,L,I,M), (C)} based on

similarities in physicochemical properties, intraclass

residue replacements are considered conservative

while interclass substitutions are non-conservative

(Dayhoff et al., 1978). Note that the overall trend is

driven by NC mutations, since C substitutions

minimally impact sequence-structure compatibility

regardless of the impact on activity. All results based

on four mutant activity categories are identically

replicated when we consider the case of two

(unaffected / affected) functional classes (Figure

3B), as defined in the Materials and Methods, and

the difference in mean residual scores for this class

pair is also statistically significant (p < 0.0001).

We alternatively consider distribution of the 630

experimental IL-3 mutants in a contingency table

MODELING CELL PROLIFERATION ACTIVITY OF HUMAN INTERLEUKIN-3 UPON SINGLE RESIDUE

REPLACEMENTS

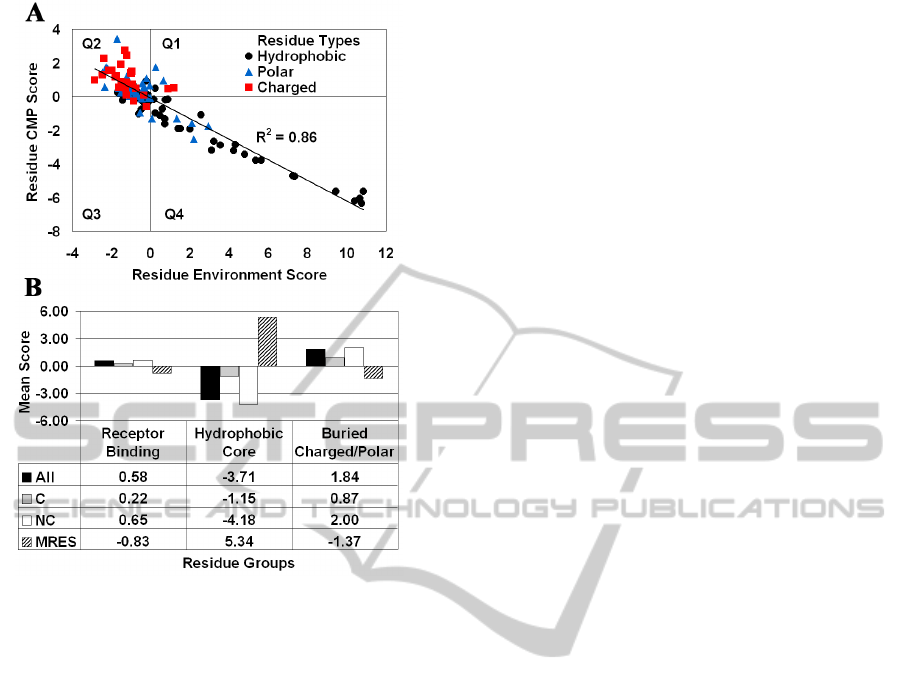
Figure 4: (A) CMP – potential profile correlation plot for

IL-3 segregates residues by polarity. (B) Effective

discrimination of the functional and structural roles carried

out by groups of IL-3 amino acid positions.

based on their activity (out of four classes) as well as

their residual scores. Using two categories of

residual scores (negative, non-negative), a chi-

square test applied to the resulting 4×2 table leads us

to reject the null hypothesis that no association

exists between activity level and residual scores (p <

0.01). Based on four residual score categories

(interval boundaries at -0.5, 0, and 0.5), a 4×4 table

is generated that yields a similar result (p < 0.0001).

3.2 Classification of Human IL-3

Residue Positions

A strong inverse correlation (R

= 0.86) exists

between the CMP profile for human IL-3, obtained

by averaging the residual scores of all amino acid

replacements at each position, and the 3D-1D

potential profile of the protein, which provides an

environment score for each position (Figure 4A). By

separately averaging residual scores of the non-

conservative (NC) and conservative (C) substitutions

at each position, a modified NC-CMP profile is

computed that is equally inversely correlated with

the 3D-1D potential profile (R

= 0.87) and reflects

the significant contribution of NC substitutions,

while a markedly diminished correlation is observed

with the modified C-CMP profile (R

= 0.42). The

plot in Figure 4A for 112 residue positions of human

IL-3 reveals a clustering according to polarity, with

the vast majority of the charged and hydrophobic

amino acids occupying quadrants 2 and 4,

respectively, and polar residues scattered within a

relatively close range of the origin.

In total, 16 residue positions in human IL-3 have

been determined to be involved in binding to the IL-

3R cell surface receptor: S17, N18, D21, E22, T25,

G42, E43, Q45, D46, M49, R94, P96, R108, F113,

K116, and E119 (Bagley et al., 1996, Klein et al.,

1997). Additionally, based on solvent accessible

surface area (http://curie.utmb.edu/getarea.html)

calculations, the 24 positions most buried in the IL-3

structure consist of 18 hydrophobic residues, with

the remaining six amino acids being either charged

or polar. We characterize each of these three groups

based on both the mean of the residue environment

scores (MRES) of the positions in the group, as well

as the mean of the mutant residual scores (All, C,

NC) for all 19 residue replacements at all positions

in the group combined (Figure 4B). Figure 4B

clearly shows that our computational

characterization effectively distinguishes these

functional and structural groups of amino acid

positions from one another.

3.3 Prediction of Human IL-3

Activity Changes

As detailed earlier in the Materials and Methods, we

first derive feature vectors for all 2128 mutants of

human IL-3 due to single residue substitutions at

positions 14 – 125, each of which includes only

seven of the EC components selected from the

corresponding perturbation vector R

mut

as well as

other predictors. In particular, we first consider

feature vectors for the 630 experimental mutants of

IL-3, each of which also has an output attribute

classifying activity as either “unaffected” or

“affected”. Performance of the random forest (RF)

algorithm on this training set is evaluated based on

running ten iterations each of 10-fold cross-

validation (CV) and 66/34 stratified random split, as

well as leave-one-out CV (LOOCV), with relatively

consistent results across all three testing methods

(Table 1). All MCC values are statistically different

from zero (p < 0.0001), indicating that predictions

are notably more correlated with the data compared

to random guessing. Table 1 also reveals that our

method outperforms by wide margins those of the

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

SIFT (http://sift.jcvi.org/) (Ng and Henikoff, 2006)

and SNAP (http://cubic.bioc.columbia.edu/services/)

(Bromberg and Rost, 2007) state-of-the-art servers

that utilize information derived from multiple

sequence alignments. Since our model does not

incorporate evolutionary information, it serves as an

orthogonal approach that is complementary to these

other methods.

Table 1: RF model performance and comparisons with

other methods.

Method Q MCC BER AUC

10-fold

CV*

0.79±0.01 0.54±0.01 0.23±0.01 0.83±0.01

66/34

split*

0.79±0.02 0.53±0.05 0.24±0.02 0.84±0.02

LOOCV 0.80 0.55 0.23 0.83

SIFT 0.59 0.26 0.37 ---

SNAP 0.68 0.33 0.33 ---

* average over ten iterations.

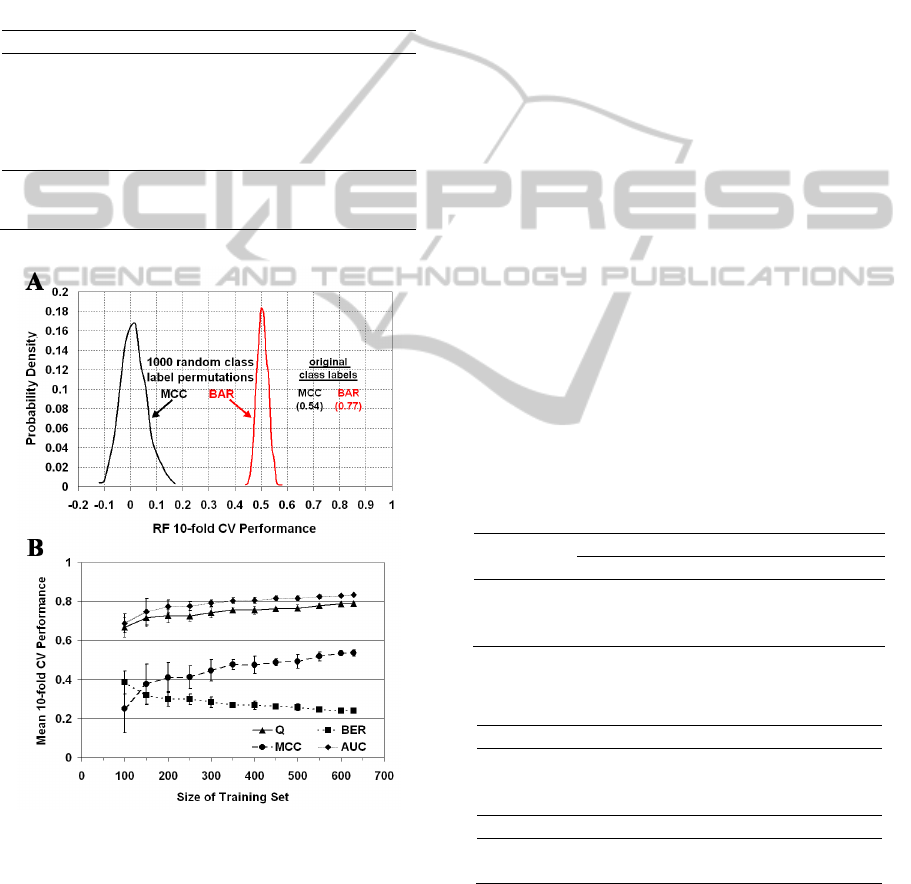
Figure 5: (A) Distribution of 10-fold CV RF prediction

performance over 1,000 permutations (random shuffles) of

the mutant IL-3 activity class labels. (B) Learning curves.

Error bars represent ± 1 std. dev. from the mean.

For a systematic approach to assessing the

statistical significance of our results in Table 1, we

generate 1,000 activity class label permutations

(random shuffles) and calculate the 10-fold CV

performance in each case based on the RF algorithm.

The distributions of MCC and BAR accuracy

measurements (Figure 5A) are narrowly centered

around zero and 0.5, respectively (MCC = 0.00 ±

0.04, BAR = 0.50 ± 0.02), with no permutation

accuracy near those obtained using the original

arrangement of the class labels (Table 1: MCC =

0.54 ± 0.01, and BAR = 1 – BER = 0.77 ± 0.01), so

the p-value for predictive power is less than 0.001.

Next, we undertake a detailed evaluation of the

LOOCV predictions on the 630 mutants of human

IL-3 in order to assess the strengths and weaknesses

of our methodology. In particular, the approach

performs best when polar and charged amino acids

are replaced with apolar residues, and vice versa,

while the least accurate predictions occur with

residue substitutions of the same polarity (Table 2).

Additionally, although overall accuracy (Q) for

surface position mutations appears to surpass that of

buried positions (Table 3), contradicting

observations noted by other researchers (Bromberg

and Rost, 2007, Capriotti et al., 2006), the surface

mutations constitute a smaller percentage of the

dataset, and their lower correlation coefficient

(MCC) suggests those correct predictions may be

more biased toward one activity class at the expense

of the other. Finally, there are nearly twice as many

mutations in helices as there are in coils, and the

helix mutation predictions are more accurate.

Table 2: LOOCV prediction performance based on side

chain polarities of the native and new amino acids at the

mutated position.

native / new

Polar Apolar Charged

Q MCC Q MCC Q MCC

Polar 0.71 0.16 0.85 0.47 0.80 0.24

Apolar 0.84 0.69 0.70 0.39 0.88 0.76

Charged 0.83 0.65 0.90 0.80 0.59 0.18

Table 3: LOOCV prediction performance based on depth

and secondary structure.

Depth Q MCC %

Buried 0.78 0.56 42

Undersurface 0.77 0.50 27

Surface 0.84 0.48 31

Secondary Structure Q MCC %

Helix 0.80 0.58 64

Coil 0.79 0.48 36

% refers to the proportion of IL-3 mutants in the dataset.

In order to assess the influence of dataset size on

trained RF model performance, learning curves are

provided in Figure 5B. We begin by applying RF

learning and 10-fold CV to each of 10 stratified

MODELING CELL PROLIFERATION ACTIVITY OF HUMAN INTERLEUKIN-3 UPON SINGLE RESIDUE

REPLACEMENTS

random samples of 100 dataset mutants, where each

subset is selected from among all 630 experimental

human IL-3 activity mutants, and mean performance

and standard deviation (std. dev.) is calculated.

Subsequent iterations involve incrementing by 50

mutants the size of the sampled datasets. The

learning curves do not appear to reach plateaus as

they approach the full dataset size of 630 mutants,

suggesting that the current RF model may be

improved upon by enlarging the training set through

possible future availability of experimental activity

data for additional IL-3 mutants.

The CfsSubsetEval attribute evaluator program in

WEKA is a tool for identifying the most influential

feature vector attributes (Frank et al., 2004). The

method evaluates various subsets of the attributes for

how highly correlated the predictors in each subset

are with the unaffected / affected activity classes

while also displaying low intercorrelation with one

another. The BestFirst search program in WEKA is

concurrently used to select the subsets for evaluation

based on a greedy hill-climbing approach, whereby

starting with a random selection of attributes, a bi-

directional search ensues in which all possible

additions or deletions of single attributes are

examined at each step (Frank et al., 2004). The

procedure is augmented with backtracking, whereby

a maximum of five consecutive, non- improving

attributes are allowed. The following ten attributes

are identified as the most highly ranked predictors:

position number; residual score; EC scores at the

second, third, and fifth nearest neighbors; primary

sequence locations of the fourth and sixth nearest

neighbors relative to the mutated position; amino

acid identity at the sixth nearest neighbor to the

mutated position; mean volume; and mean

tetrahedrality. These ten attributes span the diversity

of predictors considered in this study, underscoring

the importance of the collective set of features.

Finally as an important practical application, we

employ the RF model learned from the entire

training set of 630 mutants of human IL-3 in order to

predict the unaffected / affected class memberships

of all remaining 1498 uncharacterized single residue

IL-3 mutants. In particular, we form a test set that

contains feature vector input attributes for the 1498

mutants of IL-3 that remain to be predicted, each of

which has an unknown unaffected / affected activity

class output attribute. Based on the signals encoded

by the input attributes of their feature vectors, the

Figure 6: Human IL-3 mutational array (red = unaffected,

green = affected, white = self-substitutions; darker colors

= experimental, lighter = predicted; boxed numbers =

receptor binding, shaded = hydrophobic core, both shaded

and boxed = buried charged / polar).

RF model generates a class prediction for every IL-3

mutant in the test set. All experimental and predicted

IL-3 mutants are pooled into the array shown in

Figure 6, which concisely summarizes overall

protein mutational patterns. Columns represent

residue positions in IL-3, and rows represent the 20

possible amino acid replacements, arranged from top

to bottom in order of increasing hydrophobicity

(Kyte and Doolittle, 1982). Notably, at nearly all

receptor-binding positions for which a number of

amino acid substitutions are known to affect activity,

predictions match experimental IL-3 mutant data.

4 CONCLUSIONS

This study demonstrates the utility of a

computational mutagenesis methodology, based on

implementations of a four-body potential and the

Delaunay tessellation of protein structure, for

modeling single residue replacements in the human

interleukin-3 (IL-3) cytokine. For each IL-3 mutant,

the approach quantifies environmental perturbation

at the mutated position (i.e., the residual score) and

at all positions in its neighborhood, as defined by the

tessellation of the IL-3 protein structure. Published

experimental data include relative changes in cell

proliferation activity for 630 single residue

substitutions of IL-3, representing nearly 30% of all

such mutants in the protein. An IL-3 structure-

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

100

function relationship is elucidated with this

collection of mutants by comparing their residual

scores (measures of relative changes to sequence-

structure compatibility) with their relative activity

changes (measures of relative functional changes).

More generally, residual scores are also useful for

naturally clustering IL-3 amino acid positions based

on their polarity, as well as for distinguishing

residue groups based on their functional or structural

roles. The experimental IL-3 mutants are

subsequently represented as feature vectors, with

input attributes that include the residual score,

ordered perturbation scores for the six structurally

closest positions in the local neighborhood of the

mutated position, and additional components based

on sequence and structure, as well as an activity

category (unaffected / affected) output attribute. This

collection of feature vectors is used to train a

random forest classifier, which displays up to 80%

accuracy for mutant IL-3 activity prediction and

outperforms other well-known methods. To assist

researchers in prioritizing future IL-3 mutagenesis

experiments, activity predictions based on the

trained model are provided for all 1498 unexplored

single residue IL-3 mutants.

REFERENCES

Bagley, C. J., Phillips, J., Cambareri, B., Vadas, M. A. and

Lopez, A. F. (1996) J Biol Chem, 271, 31922-31928.

Baldi, P., Brunak, S., Chauvin, Y., Andersen, C. A. and

Nielsen, H. (2000) Bioinformatics, 16, 412-424.

Barber, C. B., Dobkin, D. P. and Huhdanpaa, H. T. (1996)

ACM Trans Math Software, 22, 469-483.

Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G.,

Bhat, T. N., Weissig, H., Shindyalov, I. N. and

Bourne, P. E. (2000) Nucleic Acids Res, 28, 235-242.

Bordner, A. J. (2008) Bioinformatics, 24, 2865-2871.

Bowie, J. U., Luthy, R. and Eisenberg, D. (1991) Science,

253, 164-170.

Breiman, L. (2001) Machine Learning, 45, 5-32.

Bromberg, Y. and Rost, B. (2007) Nucleic Acids Res, 35,

3823-3835.

Capriotti, E., Calabrese, R. and Casadio, R. (2006)

Bioinformatics, 22, 2729-2734.

Carter, C. W., Jr., LeFebvre, B. C., Cammer, S. A.,

Tropsha, A. and Edgell, M. H. (2001) J Mol Biol, 311,

625-38.

Dayhoff, M. O., Schwartz, R. M. and Orcut, B. C. (1978)

In Atlas of Protein Sequence and Structure, Vol. 5

(Ed, Dayhoff, M. O.) National Biomedical Research

Foundation, Washington D.C., pp. 345-352.

de Berg, M., Cheong, O., van Kreveld, M. and Overmars,

M. (2008) Computational Geometry: Algorithms and

Applications, Springer-Verlag, Berlin.

Fawcett, T. (2003) In Technical Report HPL-2003-4.

Hewlett-Packard Labs, Palo Alto.

Feng, Y., Klein, B. K. and McWherter, C. A. (1996) J Mol

Biol, 259, 524-541.

Frank, E., Hall, M., Trigg, L., Holmes, G. and Witten, I.

H. (2004) Bioinformatics, 20, 2479-2481.

Klein, B. K., Feng, Y., McWherter, C. A., Hood, W. F.,

Paik, K. and McKearn, J. P. (1997) J Biol Chem, 272,

22630-22641.

Kyte, J. and Doolittle, R. F. (1982) J Mol Biol, 157, 105-

132.

Ng, P. C. and Henikoff, S. (2006) Annu Rev Genomics

Hum Genet, 7, 61-80.

Olins, P. O., Bauer, S. C., Braford-Goldberg, S., Sterbenz,

K., Polazzi, J. O., Caparon, M. H., Klein, B. K.,

Easton, A. M., Paik, K., Klover, J. A. and et al. (1995)

J Biol Chem, 270, 23754-23760.

Pettersen, E. F., Goddard, T. D., Huang, C. C., Couch, G.

S., Greenblatt, D. M., Meng, E. C. and Ferrin, T. E.

(2004) J Comput Chem, 25, 1605-1612.

Qi, Y., Bar-Joseph, Z. and Klein-Seetharaman, J. (2006)

Proteins, 63, 490-500.

Sippl, M. J. (1993) J Comput Aided Mol Des, 7, 473-501.

Wang, G. and Dunbrack, R. L., Jr. (2003) Bioinformatics,

19, 1589-1591.

Zhang, S., Kaplan, A. H. and Tropsha, A. (2008) Proteins,

73, 742-53.

MODELING CELL PROLIFERATION ACTIVITY OF HUMAN INTERLEUKIN-3 UPON SINGLE RESIDUE

REPLACEMENTS

101