A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK

BOUNDS ON GENERALIZATION OF LEARNING MACHINES

Przemysław Kl˛esk

Department of Methods of Artiﬁcial Intelligence and Applied Mathematics, Westpomeranian University of Technology

ul.

Zolnierska 49, Szczecin, Poland

Keywords:

Statistical learning theory, Bounds on generalization, Cross-validation, Empirical risk minimization, Structural

risk minimization, Vapnik–Chervonenkis dimension.

Abstract:

Typically, the n-fold cross-validation is used both to: (1) estimate the generalization properties of a model

of ﬁxed complexity, (2) choose from a family of models of different complexities, the one with the best

complexity, given a data set of certain size. Obviously, it is a time-consuming procedure. A different approach

— the Structural Risk Minimization is based on generalization bounds of learning machines given by Vapnik

(Vapnik, 1995a; Vapnik, 1995b). Roughly speaking, SRM is O(n) times faster than n-fold cross-validation but

less accurate.

We state and prove theorems, which show the probabilistic relationship between the two approaches. In

particular, we show what ε-difference between the two, one may expect without actually performing the cross-

validation. We conclude the paper with results of experiments confronting the probabilistic bounds we derived.

1 INTRODUCTION AND

NOTATION

One part of the Statistical Learning Theory devel-

oped by Vapnik (Vapnik, 1995a; Vapnik, 1995b; Vap-

nik, 2006) is the theory of bounds. It provides prob-

abilistic bounds on generalization of learning ma-

chines. The key mathematical tools applied to derive

the bounds in their additive versions are Chernoff and

Hoeffding inequalities

(Vapnik, 1995b; Cherkassky

and Mulier, 1998; Hellman and Raviv, 1970; Schmidt

et al., 1995).

We use this theory to show a probabilistic rela-

tionship between two approaches for complexity se-

lection: n-fold cross-validation (popular among prac-

tioner modelers) and Structural Risk Minimization

proposed by Vapnik (rarely met in practice) (Shawe-

Taylor et al., 1996; Devroye et al., 1996; Anthony

and Shawe-Taylor, 1993; Krzy

zak et al., 2000). We

Chernoff inequality: P



|ν

− p| ≥ ε



≤ 2 exp(−2ε

I),

Hoeffding inequality: P



−EX| ≥ ε



≤ 2exp(−

2ε

−A

Meaning (respectively): observed frequencies on a sample

of size I converge to the true probability as I grows large;

analogically: means of a random variable (bounded by A

and B) converge to the expected value. It is a in-probability-

convergence and its rate is exponential.

remind that SRM is O(n) times faster than n-fold

cross-validation (since SRM does not perform any

repetitions/folds per single ﬁxed complexity, nor test-

ing) but less accurate, since the selection of optimal

complexity is based on the guaranteed generaliza-

tion risk. The bound for the guaranteed risk is ex-

pressed in terms of Vapnik-Chervonenkis dimension,

and is a pessimistic overestimation of the growth func-

tion, which in turn is overestimation of the unknown

Vapnik-Chervonenkis entropy. We formally remind

these notions later in the paper. All those overesti-

mations contribute (unfortunately) to the fact that for

a ﬁxed sample size, SRM usually underestimates the

optimal complexity and chooses too simple model.

Results presented in this paper may be regarded

as conceptually akin to results by Holden (Holden,

1996a; Holden, 1996b), where error bounds on

cross-validation and so-called sanity-check bounds

are derived. The sanity-check bound is a proof,

for large class of learning algorithms, that the er-

ror of the leave-one-out estimate is not much worse

— O(

h/I) — than the worst-case behavior of the

training error estimate, where h stands for Vapnik-

Chervonenkis dimension of given set of functions and

I stands for the sample size. The name sanity-check

refers to the fact that although we believe that under

many circumstances, the leave-one-out estimate will

Kl˛esk P..

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF LEARNING MACHINES.

DOI: 10.5220/0003121000050017

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 5-17

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

perform better than the training error (and thus jus-

tify its computational expense) the goal of the sanity-

check bound is to simply prove that it is not much

worse than the training error (Kearns and Ron, 1999).

These results were further generalized by Kearns

(Kearns and Ron, 1999; Kearns, 1995a; Kearns,

1995b) using the notion of (β

,β

)-error stability

rather than (β

,β

)-hypothesis stability

imposed on

the learning algorithm.

For the sake of comparison and to set up the per-

spective for further reading of this paper, we highlight

some differences of meaning of our results and the re-

sults mentioned above:

- we do not focus on how well the measured cross-

validation result estimates the generalization error

or how far it is from the training error in the leave-

one-out case — sanity-check bounds (Holden,

1996b; Kearns and Ron, 1999); instead, we want

to make statements about the cross-validation re-

sult without actually measuring it, thus, remaining

in the setting of the SRM framework.

- in particular we want to state probabilistically

what ε-difference one can expect between the

known Vapnik bound and the unknown cross-

validation result for given conditions of the exper-

iment,

- in the consequence, we want to be able to cal-

culate the necessary size of the training sample,

so that the ε is sufﬁciently small, and so that

the optimal complexity indicated via SRM is ac-

ceptable in the sense that cross-validation, if per-

formed, would probably indicate the same com-

plexity; this statement may seem related to the

notion of sample complexity considered e.g. by

Bartlett (Bartlett et al., 1997; Bartlett, 1997) or Ng

(Ng, 2004), but we do not ﬁnd the sample size re-

quired for the algorithm to learn/generalize “well”

but rather such a sample size so that complexity

selection via SRM gives similar results to com-

plexity selection via cross-validation,

- we do not explicitly introduce the notion of er-

ror stability for the learning algorithm, but this

We say that a learning algorithm has a (β

,β

)-error

stability, if generalization errors for two models provided by

this algorithm using respectively a training sample of size I

and a sample with size lowered to I −1 are β

-close to each

other with probability at least 1−β

. Obviously the smaller

both β

,β

are the more stable the algorithm.

We say that a learning algorithm has a (β

,β

hypothesis stability, if the two models provided by this al-

gorithm using respectively a training sample of size I and

sample with size lowered to I −1 are β

-close to each other

with probability at least 1 −β

, where closeness of models

is measured by some functional metrics, e.g. L

, L

, etc.

kind of stability is implicitly derived be means of

Chernoff-Hoeffding-like inequalities we write.

- we do not focus on the leave-one-out cross-

validation; we consider a more general n-fold non-

stratiﬁed cross-validation (also: more convenient

for our purposes); the leave-one-out case can be

read out from our results as a special case.

1.1 Notation Related to Statistical

Learning Theory

We keep the notation similar to Vapnik’s (Vapnik,

1995b; Vapnik, 1995a).

• We denote the ﬁnite set of samples as:



),(x

),.. .,(x

)



or more shortly by encapsulating pairs as

,.. .,z

where x

∈ R

are input points, y

are output val-

ues corresponding to them, and I is the set size. y

differ depending on the learning task: for classi-

ﬁcation (pattern-recognition) y

∈{1, 2,..., K} —

ﬁnite discrete set, for regression estimation y

∈R.

• We denote the set of approximating functions

(models) in the sense of both classiﬁcation or re-

gression estimation as:

{f (x,ω)}

ω∈Ω

where Ω is the domain of parameters of this set of

functions, so a ﬁxed ω can be regarded as an index

of a speciﬁc function in the set.

• The risk functional R : {f (x, ω)}

ω∈Ω

→ R ∪

{+∞} is deﬁned as

R(ω) =

x∈X

y∈Y



f (x, ω),y



p(x,y)

|{z}

p(x)p(y|x)

dydx,

(1)

where p(x) is the distribution density of in-

put points, p(y|x) is the conditional density of

system/phenomenon outputs y given a ﬁxed x.

p(x,y) = p(x)p(y|x) is the joint distribution den-

sity for pairs (x,y). In practice, p(x,y) is un-

known but ﬁxed, and hence we assume the sample

,.. .,z

} to be i.i.d.

L is the so called loss

function which measures the discrepancy between

the output y and the model f . For classiﬁcation, L

is an indicator function:



f (x, ω),y



(

0, for y = f (x,ω);

1, for y 6= f (x,ω),

(2)

Independent, identically distributed.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

and the risk functional becomes R(ω) =

x∈X

∑

y∈Y



f (x, ω),y



p(x,y)dx. For regression

estimation, L is usually chosen as the distance in

metric:



f (x, ω),y





f (x, ω) −y



, (3)

and the risk functional becomes R(ω) =

x∈X

y∈Y



f (x, ω) −y



p(x,y)dydx.

• By ω

we denote the index of the best function

f (x, ω

) in the set, such that:

R(ω

) = inf

ω∈Ω

R(ω). (4)

• Since only a ﬁnite set of samples {z

,.. .,z

} is

at disposal, we cannot count on actually ﬁnding

the best function f (x,ω

). In fact, we look for its

estimate with respect to the ﬁnite set of samples.

We deﬁne the empirical risk:

emp

(ω) =

∑

i=1

L(y

, f (x

,ω)), (5)

and by ω

we denote the index of the function

f (x, ω

) such that:

emp

(ω

) = inf

ω∈Ω

emp

(ω) (6)

— Empirical Risk Minimization principle (Vap-

nik, 1995a; Vapnik, 1995b; Vapnik and Chervo-

nenkis, 1989; Cherkassky and Mulier, 1998).

• For simpliﬁcation of notation and further consid-

erations, we introduce replacements:

(x,y) = z,



f (x, ω),y



= Q



z,ω).

In other words instead of considering the set

of approximating functions

{f (x,ω)}

ω∈Ω

, we

equivalently consider the set of error functions

{Q(z,ω)}

ω∈Ω

. It is a 1:1 correspondence

. Now,

we write the true risk as:

R(ω) =

z∈X×Y

Q(z,ω) p(z)

|{z}

p(x,y)

Q(z,ω)dF(z), (7)

and the empirical risk as

emp

(ω) =

∑

i=1

Q(z

,ω)), (8)

In the sense of all learning tasks.

Q is identical with L in the sense of their values. They

differ only in formal posing of their domains. L works on

f (x,ω) and y and maps them to error values, whereas Q

works directly on z and ω and maps them to error values.

1.2 Notation Related to

Cross-validation

In the paper, we shall consider the non-stratiﬁed vari-

ant of the n-fold cross-validation procedure (Kohavi,

1995). In each single fold (iteration) we ﬁrst permute

the data set and then we split it at the same ﬁxed point

into two disjoint subsets — a training set and a testing

set. Thus, we guarantee the randomness by permuta-

tion per each fold, and among folds we do not care to

make training sets disjoint pairwise. Since permuta-

tions are independent, hence folds are independent as

well.

Such an approach is somewhere in-between the

classical n-fold cross-validation and the bootstrap-

ping (Efron and Tibshirani, 1993). In the classical

cross-validation, all





pairs of training sets are mu-

tually disjoint (and so are testing sets) and hence folds

are dependent, whereas in the bootstrapping instead

of repeatedly analyzing subsets of data set, one re-

peatedly analyzes the subsamples (with replacement)

of the data. For more information see (Hjorth, 1994;

Weiss and Kulikowski, 1991; Fu et al., 2005).

We introduce the following notation. I

and I

stand for the size of training and testing sets respec-

tively.

n −1

Without loss of generality for theorems and proofs, let

I be dividable by n, so that I

and I

are integers.

In a single fold, let

,.. .,z

}, {z

,.. .,z

}

represent respectively the training set and the testing

set, taken as a split of the whole permuted data set

,.. ., z

}. Similarly, empirical risks calculated

as follows:

emp

(ω) =

∑

i=1

Q(z

,ω), (9)

emp

(ω) =

∑

i=1

Q(z

,ω), (10)

represent respectively the training error and the test-

ing error, calculated for any function ω.

By ω

we deﬁne the function that minimizes the

empirical training risk

emp

(ω

) = inf

ω∈Ω

emp

(ω) (11)

when the context of discussion is constrained to single

fold. When, we will need to broaden the context onto

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES

all folds, k = 1,2,.. .,n, we will write ω

to denote

the function that minimizes the empirical training risk

in the k-th fold. Therefore, the ﬁnal cross-validation

result — an estimate of generalization error — is the

mean from empirical testing risks R

emp

using func-

tions ω

C =

∑

k=1

emp

(ω

). (12)

The independence of folds can be formally ex-

pressed in the following way. For any two indices

of folds k 6= l and for any numbers A,B:

P(R

emp

(ω

) = A, R

emp

(ω

) = B)

= P(R

emp

(ω

) = A) ·P(R

emp

(ω

) = B).

We stress the independence once again, because later

on we are going to sum up several independent proba-

bilistic inequalities into one inequality, and we would

like the result to be true with the effective probability

being the product of component probabilities.

2 THE RELATIONSHIP FOR A

FINITE SET OF

APPROXIMATING FUNCTIONS

2.1 Classiﬁcation Learning Task

Similarly to Vapnik, let us start with the classiﬁcation

learning task and the simplest case of a ﬁnite set of N

indicator functions: {Q(z, ω

)}

∈Ω

, j = 1,2,.. .,N.

Not to complicate things, we will keep on writing ω

in the sense of the optimal function minimizing the

empirical risk on our ﬁnite sample of size I, instead

of writing more formally e.g. ω

j(I)

Vapnik shows (Vapnik, 1995a; Vapnik, 1995b)

that with probability at least 1 − η, the following

bound on the true risk is satisﬁed:

Q(z,ω

)dF(z)

| {z }

R(ω

)

≤

∑

i=1

Q(z

,ω

)

| {z }

emp

(ω

)

lnN −ln η

(13)

The argument is the following:



sup

1≤j≤N

R(ω

) −R

emp

(ω

) ≥ ε



≤

∑

j=1



R(ω

)−R

emp

(ω

) ≥ε



≤N ·exp(−2ε

I).

In the sense that j(I) ∈ {1, .. ., N} returns the index of

the minimizer given our data set of size I.

The last pass is true, since for each term in the sum

Chernoff inequality is satisﬁed. By substituting the

right-hand-side with small probability η and solving

for ε, one obtains the bound:

R(ω

) −R

emp

(ω

) ≤

lnN −ln η

which holds true with probability at least 1 −η simul-

taneously for all functions in the set, since it holds for

the worst. Hence, in particular it holds true for the

function ω

. And one gets the bound (13).

For the theorems to follow, we denote the right-

hand-side in the Vapnik bound by V = R

emp

(ω

) +

(lnN −lnη)/(2I).

Theorem 1. Let {Q(z,ω

)}

∈Ω

, j = 1,2,. ..,N, be

a ﬁnite set of indicator functions (classiﬁcation task)

of size N. Then, for any η > 0, arbitrarily small, there

is a small number

α(η,n) = η −

∑

k=1





(−1)

(2η)

, (14)

and the number

ε(η,I,N,n) =

n −1

+ 1

lnN −ln η



√

n +

n −1



−lnη

, (15)

such that:

|V −C| ≤ ε(η,I,N,n)

≥ 1 −α(η, n). (16)

Before we prove theorem 1, the following two re-

marks should be clear.

Remark 1. The value of α(η, n) is monotonous with

η. I.e. the smaller η we choose, the smaller α(η,n)

becomes as well. Therefore the minimum probability

measure 1 −α(η, n) is suitably large.

lim

η→0

η −

∑

k=1





(−1)

(2η)

= lim

η→0

η + 1 −

∑

k=0





(−1)

(2η)

= lim

η→0





η + 1 −(1 −2η)

| {z }

→1





= 0.

Remark 2. For the ﬁxed values of η, N, n, the value

of ε(η,I,N,n) converges to zero as the sample size I

grows large.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

This is an important remark, because it means

that both the cross-validation result C and the Vapnik

bound V converge in probability

to the same value

as the sample size grows large. Moreover, the rate of

this convergence is exponential.

Proof of Remark 2. Since N is ﬁxed, we note that

for η → 0

lnN −ln η

∼

−lnη

Therefore, for ﬁxed η, N, n there exists a constant,

say D, such that

ε(η,I,N,n) = 2

n −1

+ 1

lnN −ln η



√

n +

n −1



−lnη

≤ D

−lnη

Solving the inequality for η we obtain η ≤

exp(−2Iε

Having in mind the inequality (16), we now give

two theorems in which the absolute value sign in

|V −C| is omitted. They can be viewed as the upper

and the lower probabilistic bounds on C and they are

derived as tighter bounds than (16). Proving these two

theorems immediately implies proving the theorem 1.

Theorem 2. With probability 1 −α(η,n) or greater,

the following inequality holds true:

C −V ≤

n −1

−1

lnN −ln η



√

n +

n −1



−lnη

. (17)

Theorem 3. With probability 1 −α(η,n) or greater,

the following inequality holds true:

V −C ≤

n −1

+ 1

lnN −lnη

√

−ln η

(18)

The second result is more interesting, provided of

course that the bound is positive for given constants

η, I, N, n. Otherwise, we get zero or negative bound,

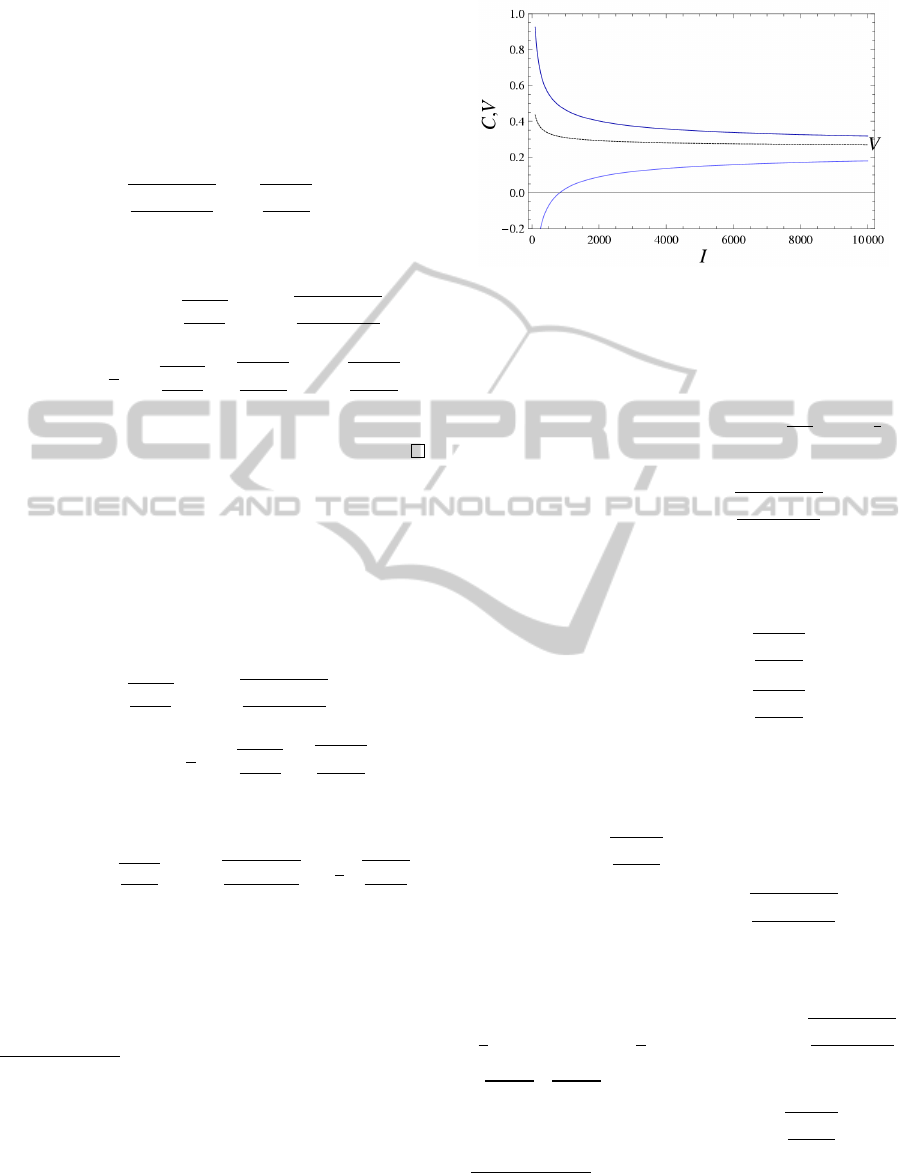
which is trivial. The ﬁg. 1 illustrates the sense of the-

orems 2 and 3.

We say that A(I) converges in probability to B, we write

A(I)

−→

I→∞

B, when for any numbers ε > 0, η > 0, there exists

a treshold size of sample I(ε, η), such that for all I ≥I(ε, η):



|A(I) −B| > ε



≤ η.

C and V can be viewed as random variables, due to ran-

dom realizations of data set {z

,. ..,z

} with joint density

p(z) (this affects C and V ) and due to random realizations

of subsets in cross-validation folds (this affects C). When

the data set {z

,. ..,z

} is ﬁxed, V is ﬁxed too.

Figure 1: Illustration of upper and lower bounds on the re-

sult of cross-validation with respect to the size of sample I.

Other constants are: η = 0.01 ⇒1 −α(η) ≈0.93, N = 100,

n = 3. With probability 1 −α(η) or greater, the result C of

cross-validation falls between the bounds.

Proof of Theorem 2. We remind: I

n−1

I, I

With probability at least 1 − η, the following

bound on true risk holds true:

R(ω

) ≤ R

emp

(ω

) +

lnN −ln η

. (19)

For the selected function ω

, ﬁxed from now on,

Chernoff inequality is satisﬁed on the testing set (em-

pirical testing risk) in either of its one-side-versions:

emp

(ω

) −R(ω

) ≤

−lnη

, (20)

R(ω

) −R

emp

(ω

) ≤

−lnη

, (21)

with probability at least 1 −η each. By joining (19)

and (20) we obtain, with probability at least

1 −2η

the system of inequalities:

emp

(ω

) −

−lnη

≤ R(ω

) ≤ R

emp

(ω

)

lnN −ln η

. (22)

After n independent folds we obtain, with probability

at least (1 −2η)

∑

k=1

emp

(ω

)

{z }

≤

∑

k=1

emp

(ω

lnN −ln η

−lnη

. (23)

The minimum probability must be 1 −2η rather than

(1 −η)

(probabilistic independence case) due to correla-

tions between inequalities. It can be also viewed as the con-

sequence of Bernoulli’s inequality.

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES

To conclude the proof, we need to relate some-

how R

emp

(ω

) from each fold to R

emp

(ω

). We need

the relation in the direction R

emp

(ω

) ≤ ···, so that

we can plug the right-hand-side of it into (23) and

keep it true. Intuitively, one might expect that choos-

ing an optimal function on a larger sample leads to a

greater empirical risk comparing to a smaller sample,

i.e. R

emp

(ω

) ≥R

emp

(ω

), because it is usually eas-

ier to ﬁt fewer data points using models of equally rich

complexities. But we don’t know with what probabil-

ity that occurs. Contrarily, on may easily ﬁnd a spe-

ciﬁc data subset for which R

emp

(ω

) ≤ R

emp

(ω

Lemma 1. With probability 1, true is the following

inequality:

∑

i=1

Q(z

,ω

) ≤

∑

i=1

Q(z

,ω

). (24)

On the level of sums of errors, not means, the

total error for a larger sample will always surpass

the total error for a smaller sample. This gives us

emp

(ω

) ≤ IR

emp

(ω

) and further:

emp

(ω

) ≤

n −1

emp

(ω

). (25)

Unfortunately it is of no use, because of the coefﬁ-

cient

n−1

. Thinking of C −V in the theorem, we need

a relation with coefﬁcients 1 at both C and V .

In (Vapnik, 1995b, pp. 124) we ﬁnd the following

helpful assertion:

Lemma 2. With probability at least 1 −2η:

Q(z,ω

)dF(z) − inf

1≤j≤N

Q(z,ω

)dF(z)

| {z }

R(ω

)

≤

lnN −ln η

−lnη

(26)

— the true risk for the selected function ω

is not far-

ther from the minimal possible risk for this set of func-

tions than

lnN−ln η

−ln η

Proof of that statement given by Vapnik is based

on two inequalities (each with probability at least 1 −

η), the ﬁrst is (13) — we repeat it here, and the second

is Chernoff inequality for the best function ω

R(ω

) −R

emp

(ω

) ≤

lnN −ln η

, (27)

emp

(ω

) −R(ω

) ≤

−lnη

. (28)

And since, by deﬁnition of ω

, R

emp

(ω

) ≥R

emp

(ω

the (26) follows.

Going back to the cross-validation procedure, we

notice that in each single fold the measure R

emp

cor-

responds by analogy to the measure R in (26) and the

measure R

emp

corresponds by analogy to R

emp

therein.

Obviously R is deﬁned on an inﬁnite and continuous

space Z = X ×Y , whereas R

emp

is deﬁned on a dis-

crete and ﬁnite sample {z

,.. .,z

}, but still from the

perspective of a single cross-validation fold we may

view R

emp

(ω

) as the “target” minimal probability of

misclassiﬁcation and R

emp

(ω

) as the observed rela-

tive frequency of misclassiﬁcation — an estimate of

that probability, remember that we take random sub-

sets {z

,.. .,z

} from the whole set {z

,.. .,z

We write

emp

(ω

) ≤ R

emp

(ω

) ≤ R

emp

(ω

−lnη

. (29)

The ﬁrst inequality is true with probability 1 by def-

inition of ω

. The second is a Chernoff inequality,

true with probability at least 1 −η.

Now, we plug (29) into (23) and obtain with prob-

ability 1 −(−

∑

k=1





(−1)

(2η)

) −η or greater:

C ≤

emp

(ω

) +

−lnη

lnN −ln η

−lnη

= R

emp

(ω

) +

n −1

lnN −ln η



√

n +

n −1



−lnη

= R

emp

(ω

) +

n −1

+ 1 −1

lnN −ln η



√

n +

n −1



−lnη

= V +

n −1

−1

lnN −ln η



√

n +

n −1



−lnη

This concludes the proof of theorem 2.

Proof of Theorem 3. The proof is analogous to the

former proof, but we need to write most of the proba-

bilistic inequalities in the different direction.

With probability at least 1 − η, the following

bound on true risk holds true:

emp

(ω

) ≤ R(ω

) +

lnN −ln η

. (30)

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

By joining (30) and (21) we obtain, with probabil-

ity at least 1 −2η the system of inequalities:

emp

(ω

) −

lnN −ln η

≤ R(ω

) ≤ R

emp

(ω

)

−lnη

. (31)

After n independent folds we obtain, with probability

at least (1 −2η)

∑

k=1

emp

(ω

) −

lnN −ln η

−

−lnη

≤

∑

k=1

emp

(ω

)

| {z }

. (32)

Again as in the former proof, we need to relate

emp

(ω

) from each fold to R

emp

(ω

), but now we

need the relation to be in the direction R

emp

(ω

) ≥

···, so that we can plug the right-hand-side of it into

(32) and keep it true.

We write

emp

(ω

)−

lnN −ln η

≤R

emp

(ω

)−

lnN −ln η

≤ R

emp

(ω

). (33)

Reading it from the right-hand-side: the second is a

(13)-like inequality but for discrete measures, which

is true with probability at least 1 −η, and the ﬁrst in-

equality is true with probability 1 by deﬁnition of ω

Now, we plug (33) into (32) and obtain with prob-

ability 1 −(−

∑

k=1





(−1)

(2η)

) −η or greater:

C ≥

emp

(ω

) −

lnN −lnη

−

lnN −lnη

−

−ln η

= R

emp

(ω

) −2

n −1

lnN −lnη

−

√

−ln η

= R

emp

(ω

) −

n −1

−1 + 1

lnN −lnη

−

√

−ln η

= V −

n −1

+ 1

lnN −lnη

−

√

−ln η

This concludes the proof of theorem 3.

Using theorems 2 and 3 we can also say what sam-

ple size I is necessary so that the the difference C −V

or V −C is less than or equal to an imposed epsilon

∗

Let us denote the right-hand-sides of upper and

lower bounds (17) and (18) by ε

and ε

respectively.

Now, suppose we want to have ε

(η,I,N,n) ≤ ε

∗

Solving it for I we get

I ≥

2ε

∗



n −1

−1



lnN −ln η



√

n +

n −1



−lnη

(34)

Similarly, if we want to have ε

(η,I,N,n) ≤ ε

∗

I ≥

2ε

∗



n −1

+ 1



lnN −lnη +

√

−ln η

(35)

To give an example: say we have a ﬁnite set of

100 functions, N = 100, we perform a 5-fold cross-

validation, n = 5, and we choose η = 0.1 and ε

∗

= 0.05. Then it follows that we need a sample

of size I ≥ 5832 so that the cross-validation result is

not worse than V + 0.05, whereas we need I ≥ 28314

so that the cross-validation result is not better than

V −0.05. And both results are true with probability

1 −α(η,n) ≈ 0.73 or greater.

Remark 3. For the leave-one-out cross-validation,

where n = I, both the lower and the upper bound

loosen to a constant of order O



−ln η



Actually, one can easily see that as we take larger

samples I → ∞ and we stick to the leave-one-out

cross-validation n = I, the coefﬁcient

n−1

standing

lnN−ln η

goes to 1, whereas the coefﬁcient

√

standing at

−ln η

goes to inﬁnity.

One might ask: for what choice of n each bound

is the tightest given η, I, N? Treating for a moment n

as a continuous variable, we impose the conditions:

∂ε

(η,I,N,n)

∂n

= 0,

∂ε

(η,I,N,n)

∂n

= 0,

and we get optimal n values:

∗

= 1 +

√

lnN −ln η +

√

−lnη

√

−lnη

, (36)

∗

= 1 +

√

lnN −ln η

√

−lnη

. (37)

Note that these values do not depend on the sample

size I.

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES

2.2 Regression Estimation Learning

Task

Now we consider the set of real-valued error func-

tions but we still stay with the simplest case when the

set has a ﬁnite number of elements. We give theorems

for the regression estimation learning task, analogous

to the ones for the classiﬁcation. We skip proofs —

the only changes they would require is the assumption

of the bounded functions, and the use of Hoeffding in-

equality in the place of Chernoff inequality.

Theorem 4. Let {Q(z,ω

)}

∈Ω

, j = 1,2,... ,N, be a

ﬁnite set of real-valued bounded functions (regression

estimation task) of size N, 0 ≤Q(z,ω

) ≤B. Then, for

any η > 0, arbitrarily small, there is a small number

α(η,n) = η −

∑

k=1





(−1)

(2η)

, (38)

and the number

ε(η,I,N,n) =

n −1

+ 1

lnN −ln η



√

n +

n −1



−lnη

, (39)

such that:

|V −C| ≤ ε(η,I,N,n)

≥ 1 −α(η, n). (40)

Theorem 5. With probability 1 −α(η,n) or greater,

the following inequality holds true:

C −V ≤

n −1

−1

lnN −ln η



√

n +

n −1



−lnη

. (41)

Theorem 6. With probability 1 −α(η,n) or greater,

the following inequality holds true:

V −C ≤

n −1

+ 1

lnN −lnη

+ B

√

−ln η

(42)

3 THE RELATIONSHIP FOR AN

INFINITE SET OF

APPROXIMATING FUNCTIONS

The simplest case with a ﬁnite number of functions

in the set has been generalized by Vapnik (Vapnik,

1995b; Vapnik and Chervonenkis, 1989; Vapnik and

Chervonenkis, 1968) onto inﬁnite sets with contin-

uum of elements by introducing several notions of the

capacity of the set of functions: entropy, annealed en-

tropy, growth function, Vapnik–Chervonenkis dimen-

sion. We remind them in brief.

First of all, Vapnik deﬁnes N

Ω

,.. .,z

) which

is the number of all possible dichotmies that can be

achieved on a ﬁxed sample {z

,.. .,z

} using func-

tions from {Q(z,ω)}

ω∈Ω

. Then, if we relax the sam-

ple the following notions of capacity can be consid-

ered:

1. expected value of ln N

Ω

— Vapnik-Chervonenkis

entropy:

Ω

(I) =

∈Z

···

∈Z

lnN

Ω

,.. .,z

)

·p(z

)···p(z

)dz

···dz

2. ln of expected value of N

Ω

— annealed entropy:

Ω

ann

(I) = ln

∈Z

···

∈Z

Ω

,.. .,z

)

·p(z

)···p(z

)dz

···dz

3. ln of supremum of N

Ω

— growth function

Ω

(I) = ln sup

,...,z

Ω

,.. .,z

It has been proved that:

Ω

(I) =

(

= ln 2

, dla I ≤ h;

≤ ln

∑

k=0





, dla I > h,

(43)

where h is the Vapnik–Chervonenkis dimension.

It has been shown (Vapnik, 1995b) that

Ω

(I)

(Jensen)

≤ H

Ω

ann

(I) ≤ G

Ω

(I) ≤ ln

∑

k=0





≤ ln





= h(1 + ln

). (44)

And the right-hand-side of (44) can be suitably in-

serted in the bounds to replace lnN.

We mention that appropriate generalizations from

the set of indicator functions (classiﬁcation) onto sets

of real-valued functions (regression estimation) can

be found in (Vapnik, 1995b) and are based on the no-

tions of: ε-ﬁnite net, set of classiﬁers for a ﬁxed real-

valued f , complete set of classiﬁers for Ω.

3.1 Classiﬁcation Learning Task

(Inﬁnite Set of Functions)

For shortness, we give only two theorems for bounds

on V −C and C −V , the bound on |V −C| is their

straightforward consequence (analogically as in pre-

vious sections).

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Theorem 7. Let {Q(z,ω)}

ω∈Ω

be an inﬁnite set of

indicator functions with ﬁnite Vapnik–Chervonenkis

dimension h. Then, with probability 1 −α(η,n) or

greater, the following inequality holds true:

C −V ≤

n −1

−1

h(1 +

) −ln



√

n +

n −1



−lnη

. (45)

Theorem 8. With probability 1 −α(η,n) or greater,

the following inequality holds true:

V −C ≤

n −1

+ 1

h(1 +

) −ln

√

−lnη

. (46)

3.2 Regression Estimation Learning

Task (Inﬁnite Set of Functions)

Again, for shortness, we give only two theorems for

bounds on V −C and C −V , the bound on |V −C| is

their straightforward consequence (analogically as in

previous sections).

Theorem 9. Let {Q(z,ω)}

ω∈Ω

be an inﬁnite set of

real-valued bounded functions, 0 ≤ Q(ω,z) ≤ B, with

ﬁnite Vapnik–Chervonenkis dimension h. Then, with

probability 1 −α(η,n) or greater, the following in-

equality holds true:

C −V ≤

n −1

−1

h(1 +

) −ln



√

n +

n −1



−lnη

. (47)

Theorem 10. With probability 1 −α(η,n) or greater,

the following inequality holds true:

V −C ≤

n −1

+ 1

h(1 +

) −ln

√

−lnη

. (48)

In practice, bounds (47) and (48) can be signiﬁ-

cantly tightened by using an estimate

B in the place of

the most pessimistic B. The estimate

B can be found

by performing just one fold of cross-validation (in-

stead of n folds) and bounding

B by: mean error on

the testing set plus a square root implied by the Cher-

noff inequality:

B ≤ R

emp

(ω

) + B

−lnη

, (49)

where η

is an imposed small probability that (49)

is not true. The reasoning behind this remark is that

in practice, typical learning algorithms rarely produce

functions f (x, ω

), in the process of ERM, having

high maximal errors. Therefore, we can insert the

right-hand-side of (49) into (47) and (48) in the place

of B. If this is done, then the minimal overall proba-

bility on bounds (47) and (48) should be adjusted to

1 −α(η,n) −η

4 EXPERIMENTS — BOUNDS

CHECKS

Results of three experiments are shown in this section,

for the following cases: (1) binary classiﬁcation, ﬁnite

set of functions, (2) binary classiﬁcation, inﬁnite set

of functions, (3) regression estimation, inﬁnite set of

functions.

4.1 Set of Functions

The form of f functions, f : [0,1]

→ [−1, 1], was

Gaussian-like:

f (x, w0,w

,.. .,w

| {z }

) =

max



−1,min



1,w

∑

k=1

exp



−

kx −µ

2σ





(50)

where centers µ

and widths σ

were generated on

random

and remained ﬁxed. Therefore we have a set

of functions linear in parameters (w

,.. .,w

). As

one can see values of f where constrained by ±1. For

the classiﬁcation learning task, the decision boundary

was arising as the solution of f (x,w

,.. .,w

) =

0. For the regression estimation, we simply looked at

the values of f (x,w

,.. .,w

). Examples of func-

tions from this set are shown in ﬁgures 2, 3

4.2 System and Data Sets

As a system y(x) we picked on random a function

from a similar class to (50) but broader, in the sense

Random intervals: µ

∈ [0, 1]

, σ

∈ [0.02, 0.1].

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES

{

, , ,··· ,

}

Figure 2: Illustration of the set of functions for classiﬁcation.

{

, , ,··· ,

}

Figure 3: Illustration of the set of functions for regression estimation.

that the number K was greater and the range of ran-

domness on σ

was larger. Data sets for both classiﬁ-

cation and regression estimation were taken by sam-

pling the system according to the joint probability

density p(x,y) = p(x)p(y|x) where we set p(x) = 1

— uniform distribution on the domain [0,1]

and

p(y|x) =

√

2πσ

exp(−

(y−y(x))

2σ

) — normal noise with

σ = 0.1.

Figure 4: System and data for classiﬁcation (a, b), regres-

sion estimation (c, d).

4.3 Algorithm of the Learning Machine

In the case of ﬁnite sets of N functions, the learn-

ing machine was simply choosing the best functions

as f (ω

) = argmin

j=1,2,...,N

emp

(ω

) or in cross-

validation folds f (ω

) = argmin

j=1,2,...,N

emp

(ω

In the case of inﬁnite sets with continuum of

elements, the learning machine was trained by the

least-squares criterion. We remark that obviously

other learning approaches can be used in this place

e.g. maximum likelihood, SVM criterion (Vapnik,

1995b; Vapnik, 1995a; M. Korze

n and Kl˛esk, 2008).

If we denote the bases exp



−

kx−µ

2σ



by g

(x) and

calculate the matrix of bases at data points

G =







1 g

) g

) ··· g

)

1 g

) g

) ··· g

)

1 g

) g

) ··· g

)







(51)

we can ﬁnd the optimal vector of w coefﬁcients by the

pseudo-inverse operation as follows:

,.. .,w

)

= (G

−1

Y, (52)

where Y = (y

,.. .,y

)

is a vector of training tar-

get values.

4.4 Experiment Results and Comments

Experiments involved trying out different settings on

all relevant constants such as: number of terms in ap-

proximating functions (K), number of functions (N)

in the case of ﬁnite sets or VC dimension (h) in case

of inﬁnite sets, sample size (I), number of cross-

validation folds (n). For each ﬁxed setting of the con-

stants, an experiment with repetitions was performed,

during which we measured the cross-validation out-

come C after each repetition. The range of these out-

comes was then compared to the interval implied by

the theorems we proved.

We show the results in two tables 1 and 2. The ﬁrst

one gives an insight on details of a single exemplary

experiment: results of its particular folds and repeti-

tions. The second one shows collective results, where

each row encapsulates 10 repetitions

It was difﬁcult to allow ourselves for more repeti-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Table 2: Collective results — each row encapsulates 10 repetitions. Tasks: c. — classiﬁcation, r.e. — regression estimation.

We denote experiments on ﬁnite or inﬁnite sets of functions by setting either N or h. For regression estimation we use

probabilistic

B calculated as R

emp

(ω

) + B

−ln η

/(2I

). In all experiments η = 0.2, hence for n = 3 the probability that

bounds are true is 1 −α(η,n) = 0.496 or greater and for n = 5 it is 1 −α(η,n) = 0.511 or greater.

no.

exp. task K N h I R

emp

(ω

) V n

bounds

[V −ε

,V + ε

]

observed

range of C

(10 repetitions)

ratio of

C inside

bounds

1 c. 50 10 - 10

0.412 0.456 3 [0.254,0.550] [0.351,0.445] 1.0

2 c. 200 10 - 10

0.345 0.389 3 [0.187,0.483] [0.352,0.385] 1.0

3 c. 200 10 - 10

0.369 0.383 3 [0.319,0.413] [0.371,0.383] 1.0

4 c. 200 10 - 10

0.396 0.410 5 [0.344,0.442] [0.386,0.401] 1.0

5 c. 50 100 - 10

0.408 0.426 3 [0.349,0.456] [0.392,0.418] 1.0

6 c. 200 100 - 10

0.336 0.354 3 [0.277,0.384] [0.332,0.338] 1.0

7 c. 50 100 - 10

0.401 0.407 3 [0.383,0.417] [0.398,0.403] 1.0

8 c. 50 - 51 10

0.181 0.250 3 [0.021,0.267] [0.181,0.184] 1.0

9 c. 200 - 201 10

0.035 0.161 3 [−0.25,0.185] [0.035,0.037] 1.0

9 r.e. 50 -

(

B = 0.193) 10

0.172 0.209 3 [0.078,0.223] [0.170,0.173] 1.0

10 r.e. 50 -

(

B = 0.194) 10

0.171 0.208 5 [0.085,0.212] [0.170,0.172] 1.0

11 r.e. 200 -

201

(

B = 0.020) 10

0.012 0.015 3 [0.006,0.016] [0.012,0.013] 1.0

12 r.e. 200 -

201

(

B = 0.020) 10

0.013 0.015 5 [0.007,0.016] [0.012,0.013] 1.0

Table 1: Details (folds, repetitions) of an exemplary exper-

iment no. 1.

no. of

expe-

riment repetition fold R

emp

(ω

)

= ω

? R

emp

(ω

)

1 1 1 0.397 false 0.444

1 1 2 0.418 true 0.369

1 1 3 0.400 false 0.468

C = 0.417

1 2 1 0.359 true 0.369

1 2 2 0.374 true 0.339

1 2 3 0.370 true 0.348

C = 0.352

1 10 1 0.403 true 0.384

1 10 2 0.395 true 0.399

1 10 3 0.394 true 0.399

C = 0.394

To comment on the results we ﬁrst remark that

before each single experiment (1-12) the whole data

set was drawn once from p(z) and remained ﬁxed

throughout repetitions. However, in the repetitions

due to the non-stratiﬁed cross-validation we parted

the data set (via permutations) into different training

and testing subsets. That is why in the table R

emp

(ω

)

and V are constant per experiment, whereas the cross-

validation varies within some observed range. In the

tions, say 100, due to large amount of results and the time-

consumption of each experiment. Yet, the observed ratio

1.0 of C falling inside bounds shows that 10 repetitions was

sufﬁcient.

table 2 we also present the interval [V −ε

,V + ε

]

which is implied by the theorems.

Please note that for all experiments the observed

range for C was contained inside [V −ε

,V + ε

] —

an empirical conﬁrmation of theoretical results. Al-

though the bounds are true with probability at least

1 − α(η,n), in this particular experiment they held

with frequency one.

In particular one can note in the table that the up-

per bounds V + ε

are closer to actual C outcomes,

while lower bounds V +ε

are more loose — a fact we

already indicated in theoretical sections. Only in the

case of experiment no. 9 the lower bound we obtained

was trivial. In the results one can also observe the

qualitative fact that both intervals tighten with 1/

√

approximately. Keep in mind that this result stops

working for the ‘leave-one-out’ cross-validation (or a

close one) and we experimented on n = 3 and n = 5.

5 EXPERIMENTS — SRM

In this section we show results of the Structural Risk

Minimization approach. We consider a structure i.e. a

sequence of nested subsets of functions: S

⊂ S

⊂

··· ⊂ S

, where each successive S



f (x, ω)



ω∈Ω

is a set of functions with Vapnik-Chervonenkis di-

mension h

, and we have h

< h

< ··· < h

. As the

best element of the structure we choose S

∗

(with VC

dimension h

∗

) for which the bound on generalization

V is the smallest.

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES

Figure 5: SRM experiments. With I = 300, optimum points reached at: h

∗

= 91 (SRM), h = 91 (C), h = 151 (true risk R).

With I = 400, optimum points reached at: h

∗

= 111 (SRM), h = 131 (C), h = 151 (true risk R).

Figure 6: Exemplary models for both regresssion estimation and classﬁcation: under complex (h = 31), accurately complex

— the best generalization (h = 151), over complex (h = 231).

Along with observing the bound V , we observe:

(1) the cross-validation result C, (2) our bounds on

C, (3) the actual true risk R calculated as an inte-

gral according to its deﬁnition (1). We pay particu-

lar attention to how the minimum point of SRM at

∗

differs from the minimum suggested by the cross-

validation and the minimum of true risk (which nor-

mally in practice is unknown). We remind that ob-

taining the result C for each h

is O(n) times more

laborious than obtaining V for each h

. See ﬁg. 5.

6 SUMMARY

In the paper we take under consideration the proba-

bilistic relationship between two quantities: Vapnik

generalization bound V and the result C of an n-fold

non-stratiﬁed cross-validation. In the literature on the

subject of machine learning (and SLT) typically the

stated results have a different focus — namely, the re-

lation between the true risk (generalization error) and

either of the two quantities V , C separately. The per-

spective we chose was intended to:

- stay in the setting of Structural Risk Minimization

approach based on Vapnik bounds,

- not perform the cross-validation procedure,

- be able to make probabilistic statements about

closeness of SRM results to cross-validation re-

sults (if such was perfomed) for given conditions

of learning experiment.

Suitable theorems about this relationship are

stated and proved. The theorems concern two learn-

ing tasks: classiﬁcation and regression estimation;

and also two cases as regards the capacity of the set of

approximating functions: ﬁnite sets and inﬁnite sets

(but with ﬁnite Vapnik-Chervonenkis dimension).

As the sample size grows large, both C and V con-

verge in probability to the same limit of true risk. The

rate of convergence is exponential.

Using the theorems, one can ﬁnd a threshold size

of sample so that the difference C −V or V −C is

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

smaller than an imposed ε. Obviously, the smaller ε

for given experiment conditions, the more frequently

one can expect to select the same optimal model com-

plexity via SRM and via cross-validation (again with-

out actually performing it).

For the special case of leave-one-out cross-

validation we observe in the consequence of bounds

we derived that at most a constant difference of order

−lnη/2) between C and V can be expected.

Additionally, we showed for what number n of

folds, the bounds (lower and upper) on the difference

are the tightest. Interestingly, as it turns out these op-

timal n values do not depend on the sample size.

Finally, shown are experiments conﬁrming statis-

tical correctness of the bounds.

ACKNOWLEDGEMENTS

This work has been ﬁnanced by the Polish Govern-

ment, Ministry of Science and Higher Education from

the sources for science within years 2010–2012. Re-

search project no.: N N516 424938.

REFERENCES

Anthony, M. and Shawe-Taylor, J. (1993). A result of vap-

nik with applications. Discrete Applied Mathematics,

47(3):207–217.

Bartlett, P. (1997). The sample complexity of pattern clas-

siﬁcation with neural networks: the size of weights is

more important then the size of the network. IEEE

Transactions on Information Theory, 44(2).

Bartlett, P., Kulkarni, S., and Posner, S. (1997). Covering

numbers for real-valued function classes. IEEE Trans-

actions on Information Theory, 47:1721–1724.

Cherkassky, V. and Mulier, F. (1998). Learning from data.

John Wiley & Sons, inc.

Devroye, L., Gyorﬁ, L., and Lugosi, G. (1996). A Proba-

bilistic Theory of Pattern Recognition. Springer Ver-

lag, New York, inc.

Efron, B. and Tibshirani, R. (1993). An Introduction to the

Bootstrap. London: Chapman & Hall.

Fu, W., Caroll, R., and Wang, S. (2005). Estimating mis-

classiﬁcation error with small samples via bootstrap

cross-validation. Bioinformatics, 21(9):1979–1986.

Hellman, M. and Raviv, J. (1970). Probability of error,

equivocation and the chernoff bound. IEEE Transac-

tions on Information Theory, IT-16(4):368–372.

Hjorth, J. (1994). Computer Intensive Statistical Methods

Validation, Model Selection, and Bootstrap. London:

Chapman & Hall.

Holden, S. (1996a). Cross-validation and the pac learning

model. Technical Report RN/96/64, Dept. of CS, Uni-

versity College, London.

Holden, S. (1996b). Pac-like upper bounds for the sample

complexity of leave-one-out cross-validation. In 9-th

Annual ACM Workshop on Computational Learning

Theory, pages 41–50.

Kearns, M. (1995a). A bound on the error of cross-

validation, with consequences for the training-test

split. In Advances in Neural Information Processing

Systems 8. MIT Press.

Kearns, M. (1995b). An experimental and theoretical com-

parison of model selection methods. In 8-th Annual

ACM Workshop on Computational Learning Theory,

pages 21–30.

Kearns, M. and Ron, D. (1999). Algorithmic stabil-

ity and sanity-check bounds for leave-one-out cross-

validation. Neural Computation, 11:1427–1453.

Kohavi, R. (1995). A study of cross-validation and boostrap

for accuracy estimation and model selection. In In-

ternational Joint Conference on Artiﬁcial Intelligence

(IJCAI).

Krzy

zak, A. et al. (2000). Application of structural risk min-

imization to multivariate smoothing spline regression

estimates. Bernoulli, 8(4):475–489.

M. Korze

n, M. and Kl˛esk, P. (2008). Maximal mar-

gin estimation with perceptron-like algorithm. In

L. Rutkowski, R. Tadeusiewicz R., L. Z. J. Z., editor,

Lecture Notes in Artiﬁcial Intelligence, pages 597–

608. Springer.

Ng, A. (2004). Feature selection, l1 vs. l2 regularization,

and rotational invariance. In 21-st International Con-

ference on Machine learning, ACM International Con-

ference Proceeding Series, volume 69.

Schmidt, J., Siegel, A., and Srinivasan, A. (1995).

Chernoff-hoeffding bounds for applications with lim-

ited independence. SIAM Journal on Discrete Mathe-

matics, 8(2):223–250.

Shawe-Taylor, J. et al. (1996). A framework for structural

risk minimization. COLT, pages 68–76.

Vapnik, V. (1995a). The Nature of Statistical Learning The-

ory. Springer Verlag, New York.

Vapnik, V. (1995b). Statistical Learning Theory: Inference

from Small Samples. Wiley, New York.

Vapnik, V. (2006). Estimation of Dependences Based on

Empirical Data. Information Science & Statistics.

Springer, US.

Vapnik, V. and Chervonenkis, A. (1968). On the uniform

convergence of relative frequencies of events to their

probabilities. Dokl. Aka. Nauk, 181.

Vapnik, V. and Chervonenkis, A. (1989). The necessary

and sufﬁcient conditions for the consistency of the

method of empirical risk minimization. Yearbook of

the Academy of Sciences of the USSR on Recognition,

Classiﬁcation and Forecasting, 2:217–249.

Weiss, S. and Kulikowski, C. (1991). Computer Systems

That Learn. Morgan Kaufmann.

A RELATIONSHIP BETWEEN CROSS-VALIDATION AND VAPNIK BOUNDS ON GENERALIZATION OF

LEARNING MACHINES