SYNCHRONISATION OF BIOLOGICAL CLOCK SIGNALS

Capturing Coupled Repressilators from a Control Systems Perspective

Thomas Hinze, Mathias Schumann and Stefan Schuster

Department of Bioinformatics, Friedrich Schiller University Jena, E.-Abbe-Platz 1-4, D-07743 Jena, Germany

Keywords:

Chronobiology, Coupled repressilators, Reaction-diffusion kinetics, Internal/external clock synchronisation,

Control system, Phase-locked loop.

Abstract:

Exploration of chronobiological systems emerges as a growing research ﬁeld within bioinformatics focusing

on various applications in medicine, agriculture, and material sciences. From a systems biological perspective,

the question arises whether biological control systems for regulation of oscillative signals and their technical

counterparts utilise similar mechanisms. If so, modelling approaches and parameterisation adopted from build-

ing blocks can help to identify general components for clock synchronisation. Phase-locked loops could be an

interesting candidate in this context. Both, biology and engineering, can beneﬁt from a uniﬁed view. In a ﬁrst

experimental study, we analyse a model of coupled repressilators. We demonstrate its ability to synchronise

clock signals in a monofrequential manner. Several oscillators initially deviate in phase difference and fre-

quency with respect to explicit reaction and diffusion rates. Accordingly, the duration of the synchronisation

process depends on dedicated reaction and diffusion parameters whose settings still lack to be sufﬁciently

captured by comprehensive tools like the Kuramoto approach.

1 INTRODUCTION

In both spheres, biological and technical systems, os-

cillatory signals play a major role in order to trigger

and control time-dependent processes. Core oscilla-

tors are the simplest devices for generation of contin-

uously running clock signals. To this end, signal pro-

cessing units consisting of at least one feedback loop

can sufﬁce (Russo and di Bernardo, 2009). So, it is

no surprise that probably numerous evolutionary ori-

gins led to oscillative reaction networks while inde-

pendently technical attempts succeeded in construc-

tion of single clocks or clock generators.

The situation becomes more complicated if sev-

eral of those core oscillators start to interact. Re-

sulting biological systems are commonly driven to

achieve a synchronous behaviour towards an evolu-

tionary advantage. Correspondingly, clock synchro-

nisation in technical systems is frequently inspired by

the need to follow a global time. Interestingly, the

formalisation of clock synchronisation processes is

quite distant from each other. While in distributed

computer systems, stepwise algorithmic approaches

(like Berkeley or Christian’s method, (Tanenbaum

and van Steen, 2001)) predominate, biological sys-

tems adjust their clock signals more gradually. Its

formalisation is either based on reaction-diffusion ki-

netics or employs the more abstract Kuramoto method

(Kuramoto, 1984), an analytic signal coherence mea-

sure restricted to sinusoidal signal shape to counteract

phase shift between each pair of core oscillators.

We deﬁne different temporally oscillating signals

to be synchronous to each other if and only if they

meet three conditions: (1) The oscillatory signal must

run undamped to avoid signal weakening. (2) Asymp-

totical or total harmonisation of the oscillatory sig-

nals meaning that after a ﬁnite amount of time called

sync

(time to synchronisation), both temporal sig-

nal courses converge within an arbitrarily small ε-

neighbourhood. (3) The resulting oscillatory sig-

nal after t

sync

has to be monofrequential to ensure

chronoscopy (constant progression of time measure).

The central prerequisite of a core oscillator to

be capable of synchronisation to others is its abil-

ity to vary its oscillation frequency within a speci-

ﬁed range (Granada and Herzel, 2009). This variation

can be achieved by forcing, by resetting, or by spe-

ciﬁc selective perturbations affecting the oscillating

signal. Without any external inﬂuences, core oscilla-

tors resume their individual free-running oscillatory

behaviour, mostly by loosing their synchronicity.

Topologically, clock synchronisation can be ac-

101

Hinze T., Schumann M. and Schuster S..

SYNCHRONISATION OF BIOLOGICAL CLOCK SIGNALS - Capturing Coupled Repressilators from a Control Systems Perspective.

DOI: 10.5220/0003121301010106

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 101-106

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

complished by two different strategies called exter-

nal and internal (Pikovsky et al., 2001). External

strategies comprise a central leading clock that propa-

gates its time signal throughout the whole network of

downstream core oscillators which adjust their indi-

vidual signals by accelerating or slowing down their

frequency for a certain amount of time. Here, we ob-

serve an unidirectional coupling from the leading cen-

tral clock to all others. In contrast, internal strategies

aim at a mutual clock exchange between the network

members. The coupling topology is mostly bidirec-

tional, and each involved core oscillator is going to

adjust its signal based on a weighted sum of the sig-

nals released by its adjacent clocks.

Within a case study, we exemplify internal syn-

chronisation by a biological system composed of

bidirectionally coupled repressilators. To this end,

we model the entire gene regulatory networks using

reaction-diffusion kinetics. Afterwards, we conduct

two comprehensive simulation studies. The ﬁrst one

discloses the time to synchronisation subject to ini-

tial phase shift between the elementary repressilators.

Its balanced diffusion rate acts as coupling strength.

It appears that synchronisation of initially antipha-

sic signals is most time-consuming for weak coupling

while it has a negligible effect for strong coupling.

A second simulation study investigates the synchro-

nisation behaviour with respect to different initial fre-

quencies of the single repressilators. The obtained

numerical results are envisioned to identify building

blocks and their parameterisation towards composi-

tion of a control system following the concept of

phase-locked loops.

2 INTERNAL

SYNCHRONISATION:

COUPLED REPRESSILATORS

2.1 Reaction Network and Kinetics

We identiﬁed a network of bidirectionally coupled re-

pressilators to be an appropriate candidate to explore

internal synchronisation within a biological system.

A repressilator is a gene regulatory network consist-

ing of three focal proteins (LacI, TetR, cI) that mu-

tually inhibit their expression from genes (lacI, tetR,

cI) (Elowitz and Leibler, 2000). We employ a system

composed of two coupled repressilators located in

two adjacent cells inspired by Garcia-Ojalvo (Garcia-

Ojalvo et al., 2004), see Fig. 1.

Let TetR be a protein able to migrate between the

cells, it acts as coupling element. Its diffusion rate diff

speciﬁes the variable bidirectional coupling strength.

Figure 1: Network topology of the TetR-coupled repressi-

lator model with diffusion between both core oscillators.

The dynamical behaviour of the network can be spec-

iﬁed by reaction-diffusion kinetics based on corre-

sponding ordinary differential equations (ODEs). For

species names in the ODEs, we abbreviate (LacI,

TetR, cI) = (lp, tp, cp) for the proteins and (lacI, tetR,

cI) = (lr, tr, cr) for the mRNA. The set of equations

for each single repressilator reads:

d lp

d t

= k

· lr− k

· lp

d tp

d t

= k

· tr− k

· tp− diff·tp+ diff· tp

external

d cp

d t

= k

· cr− k

· cp

d lr

d t

= α

α· k

+ cp

− k

· lr− k

lr2

· lr

d tr

d t

= α

α· k

+ lp

− k

· tr− k

tr2

· tr

d cr

d t

= α

α· k

+ tp

− k

· cr− k

cr2

· cr

We utilise the parameter setting α

= 0.03, α =

29.97, k

= 40, n = 3, k

{lp,tp,cp}

= 0.069, k

{lr,tr,cr}

6.93, k

{lr2,tr2,cr2}

= 0.347 resulted from a parame-

ter ﬁtting based on the available experimental data

(Garcia-Ojalvo et al., 2004). Additionally, the ini-

tial species concentrations in case of no phase shift

are chosen at the limit cycle, e.g. lr = 0.819, tr =

2.388, cr = 0.068, lp = 36.263, tp = 166.685, cp =

64.26.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

102

The repressilator’s oscillation frequency mainly

depends on the degradation reaction rates. Diffusion

of TetR proteins from one repressilator to its adja-

cent counterpart causes the same effect. This allows

to control the frequency just by forcing using a sus-

tained dissipation of diffusing TetR proteins. Fig. 2

illustrates a typical synchronisation run.

time steps

TetR abundance

Figure 2: Typical synchronisation run of two coupled re-

pressilators, coupling strength diff= 0.04, initial phase shift

182

◦

(arbitrarily chosen). Simulation carried out with Co-

pasi using ODEs and parameter settings given in Sec. 2.1.

2.2 Synchronising Initial Phase Shifts

For the synchronisation study, we set up both repres-

silator’s initial concentrations at the individual limit

cycle in order to avoid effects occurring within the

transient phase (stabilisation phase). Afterwards, a

two-dimensional parameter scan was conducted vary-

ing the initial phase shift of both repressilators be-

tween 0

◦

and 360

◦

and simultaneously varying the

coupling strength within the relevant range diff= 0.01

to 0.13 (weak to strong coupling). The time to syn-

chronisation was obtained assuming a signal conver-

gence of one minute per day (ε-neighbourhood’s in-

terval length =

1440

of oscillation period), see Fig. 3.

The simulation study exhibits a correlation be-

tween coupling strength (diff) and time to synchro-

nisation. Since a strong coupling (diff = 0.13) has

a more signiﬁcant effect on the adjacent repressila-

tor’s behaviour, synchronisation is achieved fast. In

this case, even the inﬂuence of different initial phase

shifts can be widely neglected. The situation becomes

different when considering a weak coupling. Here,

the initial phase shift predominantly determines the

time to synchronisation. Initial antiphase rhythmicity

(phase shift 180

◦

) between both repressilators causes

0 50 100 150 200 250 300 350

2000 4000 6000 8000 10000 12000 14000

diff = 0.01

diff = 0.04

diff = 0.07

diff = 0.1

diff = 0.13

180°

phase shift φ

time to synchronize

initial phase shift

time to synchronisation

diff = 0.01

diff = 0.04

diff = 0.07

diff = 0.10

diff = 0.13

Figure 3: Time to synchronisation subject to various initial

phase shifts. Parameter diff= 0.01, . . . , 0.13 denotes cou-

pling strength from weak to strong coupling. Initial an-

tiphase rhythmicity (phase shift 180

◦

) between both repres-

silators causes the highest effort to synchronise both oscil-

latory signals by mutual forcing.

the highest effort to synchronise both oscillatory sig-

nals by mutual forcing. In this context, it is inter-

esting to mention that the ability of the repressilator

coupling to synchronise initial antiphase rhythmicity

is a direct consequence of the (slight) asymmetric os-

cillatory signal shape. While symmetric oscillation

curves (like sinusoidal signals) persist in antiphase

when coupled, hence unable to synchronise, asym-

metric curves (like spiking signals) entail a kind of

unbalanced response to forcing. There is no equi-

librium between forcing effects shortening and those

advancing the oscillatory period. The remaining ef-

fect is sufﬁcient to initiate synchronisation. The slight

asymmetry of the diagram in Fig. 3 also results from

the asymmetric shape of the repressilator’s oscilla-

tory signal. Interestingly, a medium coupling strength

(diff = 0.07) generates a behaviour in which time

to synchronisation for increasing initial phase shift

can be compensated within a range of approximately

◦

. . . 100

◦

and 260

◦

. . . 310

◦

, respectively.

2.3 Synchronisation of Different Initial

Frequencies

We demonstrate the ability of the repressilator cou-

pling to synchronise different initial frequencies in the

elementary repressilators. To this end, individual pro-

SYNCHRONISATION OF BIOLOGICAL CLOCK SIGNALS - Capturing Coupled Repressilators from a Control Systems

Perspective

103

tein degradation rates k

, k

had been modiﬁed in

conjunction with setting up all initial concentrations

at the individual limit cycle. From this, we conducted

a parameter scan taking into account the ratios of ini-

tial frequencies.

The purpose of this case study is to answer four

questions: (1) Is there any synchronisation window, a

continuous range of parameter settings, that runs the

entire system into synchronisation? In other words,

can we detect a variant of a so-called Arnold tongue?

(2) If a synchronisation window could be identiﬁed,

which of the three conditions necessary for synchro-

nised oscillations become violated by leaving the de-

limiting parameter settings? (3) How is the time

to synchronisation distributed within the synchroni-

sation window? (4) Which synchronous frequency

does result from the initially different frequencies af-

ter synchronisation?

While question (1) seems suitable to be answered

in part using the Kuramoto method (Kuramoto, 1984),

an analytical ODE-based technique, a sufﬁcient clar-

iﬁcation of questions (2), (3), and (4) requires an ex-

plorative simulation study. An essential part of this

study is the calculation of the frequencies governed

by an oscillatory signal. To this end, we utilise the

discrete Fast Fourier Transformation (FFT) for long-

term data accompanied by sampling and counting of

local oscillatory signals maxima or minima for short-

time data series. Time to synchronisation is again

measured by the number of elapsed time steps up to

convergence of one minute per day (cf. Sec. 2.2).

If synchronisation is obtained, we can distinguish

two qualitative scenarios characterised by the result-

ing synchronous frequency in relation to either initial

frequencies.

Fig. 4 depicts a typical temporal course towards

synchronisation of two marginally different initial

frequencies (solid lines). During the synchronisa-

tion process, both frequencies converge to a common

value (dashed curves). This value deviates from both

initial frequenciesbut arises in between. The synchro-

nisation itself runs rather fast.

In contrast, a stronger – however slight – deviance

of initial frequencies turns the synchronisation into a

ﬁnal frequencyasymptotically convergingto the max-

imum initial frequency, see Fig. 5 for an example.

Here, the synchronisation process takes more time.

The latter case coincides with arrival at the limits

of the synchronisation window marking the maximal

deviance of initial frequencies leading to synchroni-

sation. Inside the synchronisation window, the syn-

chronous frequency becomes adjusted in between of

both initial frequencies, and the more we approach to-

wards the boundaries of the synchronisation window,

0.0015 0.0016 0.0017

time steps

synchronous frequency

2000 4000 6000 8000

initial frequency cell 1 (0.001645)

initial frequency cell 2 (0.001578)

frequencies cell 1 towards synchronisation

frequencies cell 2 towards synchronisation

Figure 4: Typical temporal course towards synchronisation

of two marginally different initial frequencies (solid lines)

converging to a common value (dashed curves). Coupling

strength: diff = 0.01, ratio of initial frequencies:

0.001645

0.001578

≈

1.042. Synchronous frequency: 0.001616.

0.0015 0.0016 0.0017

time steps

synchronous frequency

2000 4000 6000 8000

initial frequency cell 1 (0.001691)

initial frequency cell 2 (0.001578)

frequencies cell 1 towards synchronisation

frequencies cell 2 towards synchronisation

Figure 5: Typical temporal course towards synchronisa-

tion at the boundary of the synchronisation window. Syn-

chronous frequency asymptotically reaches the maximum

of either initial frequencies (dashed curves). Initial frequen-

cies marked by solid lines. Coupling strength: diff = 0.01,

ratio of initial frequencies:

0.001691

0.001578

≈ 1.072. Synchronous

frequency: 0.001690.

the synchronous frequency converges to the maxi-

mum of both initial frequencies.

We obtain a synchronisation window delimited by

polyfrequential oscillations with respect to the ratios

of initial frequencies and loss of undamped oscillation

with respect to the coupling strength, see Fig. 6. We

checked whether an oscillatory signal is undamped or

not by evaluating the eigenvalues of the Jacobian ma-

trix derived from the ODEs specifying the reaction-

diffusion kinetics.

Moreover, the simulation results indicate that a

medium coupling strength (diff = 0.07) enables syn-

chronisation within the largest ratio of initial frequen-

cies ranging from 0.697 to 1.294. This means in terms

of systems application for clock synchronisation that

a clock signal can be temporarily slowed down (post-

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

104

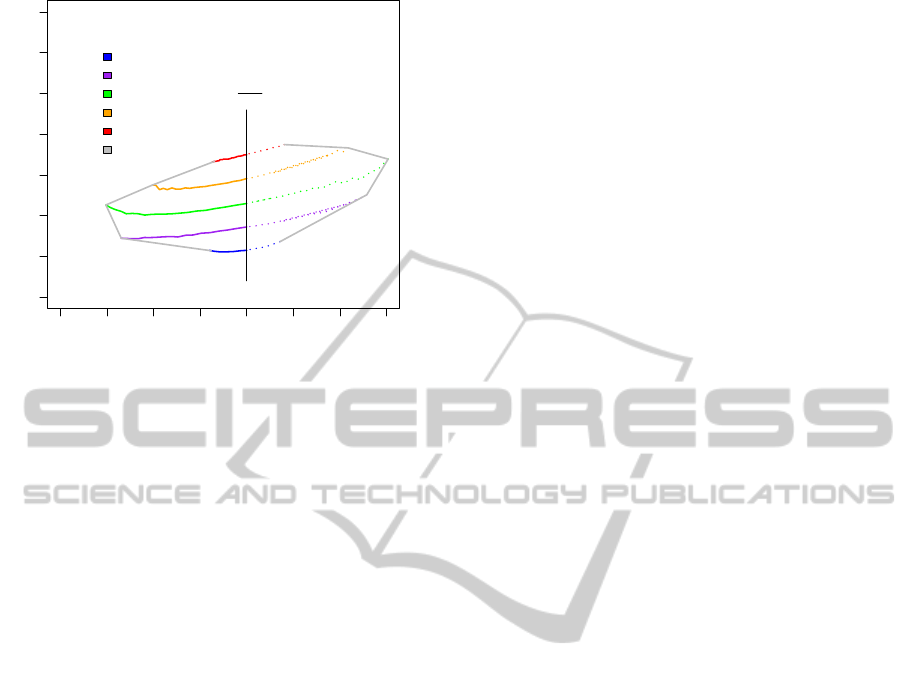
0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3

0.0010 0.0020 0.0030 0.0040

diff = 0.01

diff = 0.04

diff = 0.07

diff = 0.1

diff = 0.13

min/max Quotient

Freq 1

Freq 2

== 1

frequency parameter ratio

synchronized frequency

ratio of initial frequencies

synchronous frequency

Figure 6: Synchronisation window: ratios of initial fre-

quencies subject to synchronous frequency considering a

variety of relevant coupling strengths diff = 0.01, . . . , 0.13

(variant of an Arnold tongue, a circle map disclosing de-

pendencies of system parameters within a range of stable

oscillation). Due to the bidirectionally balanced coupling

strength, an almost symmetric synchronisation window can

be obtained which is delimited by polyfrequential oscilla-

tions with respect to the ratios of initial frequencies and loss

of undamped oscillation with respect to coupling strength.

pone the clock) and speeded up (put the clock for-

ward) with up to approximately 30% of its velocity.

The knowledge about parameterisation, capabilities

and limits of an oscillatory system envisioned to act

as a biological clock is essential for subsequent inte-

grative modelling, synthesis, and implementation of a

corresponding frequency control system.

Bidirectionally coupled repressilators exhibit the

ability to synchronise their oscillatory signals by forc-

ing. It has been observed that arbitrary initial phase

shifts become compensated while an adaption of the

entire system to different initial frequencies of the sin-

gle oscillators spans a synchronisation window.

3 EXTERNAL

SYNCHRONISATION:

REPRESSILATOR AS CORE

OSCILLATOR

The repressilator can be seen as an advantageous tool

to conduct external synchronisation when embedded

as core oscillator into a frequency control system

based on the concept of phase-locked loop (Stensby,

1997), PLL for short. These systems adapt their oscil-

latory output signal to an external stimulus acting as

reference. In contrast to internal synchronisation, the

external stimulus is not affected. A biological exam-

ple is given by circadian clocks that harmonise their

oscillatory behaviour with the daily light-dark rhyth-

micity (Bell-Pedersen, 2005). Here, the light acts

as external stimulus. Fig. 7 illustrates the general

scheme of PLL. One or several coupled core oscil-

lators constitute its central part. The signal compara-

tor as downstream module determines the difference

between core oscillator output and external stimulus.

The phase shift between either signals is an ideal can-

didate to form an error signal able to adjust the core

oscillator. The error signal passes a global feedback

path along with damping and delay by dedicated low-

pass ﬁlters. Finally, the resulting smoothened signal

inﬂuences the core oscillator(s) by increasing or de-

creasing its frequency.

We expect to demonstrate that all functional mod-

ules required for a PLL control system can be imple-

mented as interacting reaction networks. Both mod-

ules, signal comparator and global feedback path, ef-

ﬁciently employ low-pass ﬁlters. Signal transduc-

tion cascades found in cell signalling networks are

a common biological motif to cover the functional-

ity of low-pass ﬁlters (Marhl et al., 2005). Here, a

focal protein alters its chemical state according to a

trigger signal. Here, a chemical state is speciﬁed by

addition or removal of phosphate groups to/from the

focal protein. In case of low-frequency triggers, the

subsequent modiﬁcation of the chemical state can fol-

low. Along with increasing frequency of the trigger,

a threshold exists denoting that the reaction system is

now too slow to follow the trigger and ends up in a

steady state by means of a chemical equilibrium.

Having a chemical low-pass ﬁlter at hand, the

functionality of the global feedback path is com-

pletely covered. The signal comparator beneﬁts from

low-pass ﬁlters to obtain the fundamental frequency

of both signals, core oscillator output and external

stimulus. Then, the phase shift between both signals

or the signal difference, respectively, can be extracted

by performing arithmetic operations. Reaction net-

works to this task are effectively feasible assuming

that substrate species concentrations encode operands

while product species concentrations (in steady state)

constitute the operational output (Hinze et al., 2009).

For example, the set of two reactions X

+ X

→ Y

and degradation Y →

0 in conjunction with mass-

action kinetics conducts a multiplication of the form

Y = X

(0) · X

(0) with initial concentrations X

(0)

and X

(0) as multipliers. Addition, non-negative sub-

traction, and division can be expressed in a similar

way. Altogether, this allows construction of a PLL

explicitly composed of reaction-diffusion networks.

SYNCHRONISATION OF BIOLOGICAL CLOCK SIGNALS - Capturing Coupled Repressilators from a Control Systems

Perspective

105

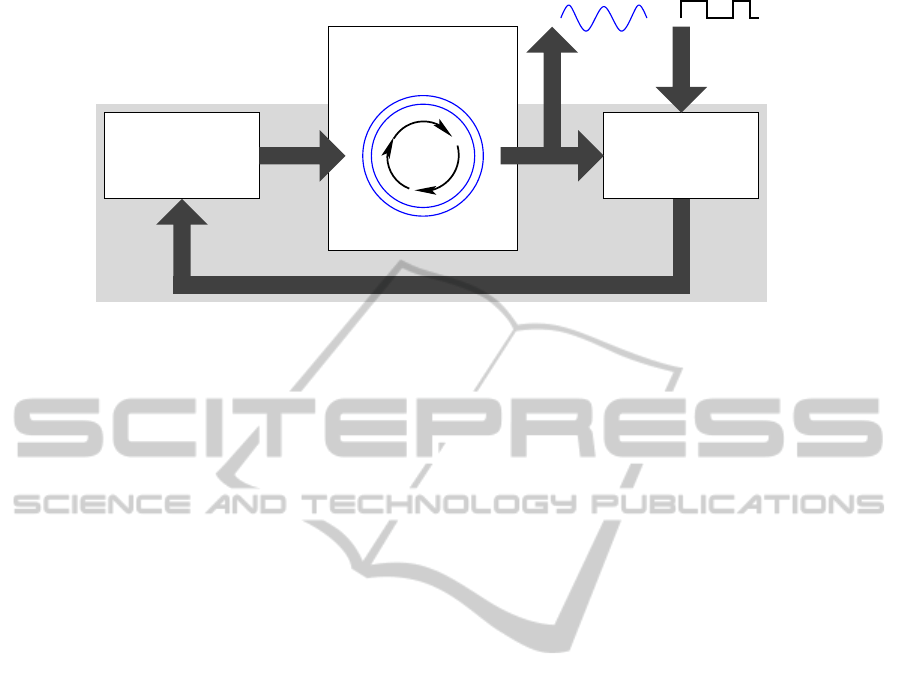
coupled

one or several

core oscillator(s)

local feedback(s)

global feedback path

damping and delay)

(loop filter for

affects

frequency

signal

tuning

signal comparator

frequency deviation)

(phase difference or

signal

output (reference)

stimuli

external

error

signal

Figure 7: General scheme of a frequency control system based on the concept of phase-locked loop (PLL). The system adapts

its oscillatory output signal to an external stimulus acting as reference for external synchronisation.

4 CONCLUSIONS

Bidirectionally coupled repressilators synchronise

their oscillatory signals by forcing. Arbitrary initial

phase shifts become compensated while adaption to

different initial frequencies spans a synchronisation

window. Coupled repressilators can be seen as a part

of a biological control system based on the concept

of phase-locked loops. Further research has been

directed to ﬁnalise the entire frequency control sys-

tem by integration of additional components for sig-

nal comparison and damping, demonstrated by low-

pass ﬁlters biologically implemented as speciﬁc sig-

nal transduction cascades. The simulations described

in this paper were carried out using Copasi (Hoops,

2006), statistical evaluation using [R].

ACKNOWLEDGEMENTS

We gratefully acknowledge funding from the German

Federal Ministry of Education and Research (project

no. 0315260A, Research Initiative in Systems Biol-

ogy).

REFERENCES

Bell-Pedersen, D. (2005). Circadian rhythms from multiple

oscillators: lessons from diverse organisms. Nat. Rev.

Genet., 6:544–556.

Elowitz, M. B. and Leibler, S. (2000). A synthetic oscil-

latory network of transcriptional regulators. Nature,

403:335–338.

Garcia-Ojalvo, J., Elowitz, M., and Strogatz, S. (2004).

Modeling a synthetic multicellular clock: repressila-

tors coupled by quorum sensing. Proc. Natl. Acad.

Sci. U.S.A., 101:10955–10960.

Granada, A. and Herzel, H. (2009). How to achieve fast

entrainment? the timescale to synchronization. PLoS

ONE 4, e7057.

Hinze, T., Fassler, R., Lenser, T., and Dittrich, P. (2009).

oscillating and catalytic chemical reactions modelled

using mass-action kinetics. International Journal of

Foundations of Computer Science, 20(3):411–426.

Hoops, S. (2006). COPASI – a COmplex PAthway SImula-

tor. Bioinformatics, 22:3067–3074.

Kuramoto, Y. (1984). Chemical oscillations, waves, and

turbulences. Springer.

Marhl, M., Perc, M., and Schuster, S. (2005). Selective reg-

ulation of cellular processes via protein cascades act-

ing as band-pass ﬁlters for time-limited oscillations.

FEBS Letters, 579(25):5461–5465.

Pikovsky, A., Rosenblum, M., and Kurths, J. (2001). Syn-

chronization: A universal con- cept in nonlinear sci-

ences. Cambridge University Press.

Russo, G. and di Bernardo, M. (2009). How to synchronize

biological clocks. Journal of Computational Biology,

16:379–393.

Stensby, J. (1997). Phase-locked loops. CRC Press.

Tanenbaum, A. S. and van Steen, M. (2001). Distributed

Systems: Principles and Paradigms. Prentice Hall In-

ternational.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

106