
UNRAVELLING BUENO DE MESQUITA’S
GROUP DECISION MODEL
Jason B. Scholz, Gregory J. Calbert and Glen A. Smith
C3I Division, Defence Science and Technology Organisation, PO Box 1500, Edinburgh, South Australia
Keywords: Multi-agent theory, Group decision making, Expected utility, Alliance, Risk, Influence.
Abstract: The development of societies of human and machine agents should benefit from an understanding of human
group decision processes. Political Scientist and Professor, Bruce Bueno De Mesquita has made significant
claims for the predictive accuracy of his computational model of group decision making, receiving much
popular press including newspaper articles, books and a television documentary entitled “The New
Nostradamus”. Despite these and many journal and conference publications related to the topic, no clear
elicitation of the model exists in the open literature. We expose and present the model by careful navigation
of the literature and illustrate the soundness of our interpretation by replicating De Mesquita’s own results.
We also discuss concerns regarding model sensitivity and convergence.
1 INTRODUCTION
There is little doubt that some of the greatest social
challenges for the future of mankind include
terrorism, war, climate change, poverty, and
economics. So, the pursuit of an integrated theory
capable of explanation and prediction of group
decision outcomes is a worthy endeavour. Such
efforts, often classed under the realm of
computational political science, aim to form testable
yet tractable models for human agency (Kollman et
al, 2010). Bueno De Mesquita (herein abbreviated to
BDM) has laid claims to such an achievement. An
example prediction was “…the ability to dominate
Iran’s politics resides with Khamenei and
Rafsanjani. And between these two – though the
contest is close – the advantage seems to lie with
Khamenei.” (BDM, 1984, p. 233)
The accuracy of this prediction is demonstrated
by the fact that Khamenei succeeded Khomeinei as
Supreme Leader of Iran in June 1989 and Rafsanjani
became the fourth president of Iran in August 1989.
BDM’s model of group decision making
considers conflict and agreement, and is based on
expected utility theory. BDM (1997) states:
The model itself depicts a game in which
actors simultaneously make proposals, and
exert influence on one another. They evaluate
options and build coalitions by shifting
positions on the issue in question. The above
steps are repeated sequentially until the issue
is resolved. (p. 238)
A New York Times article by Thomson (2009) gives
some insight into why the model has never been
fully disclosed:
…Bueno de Mesquita does not publish the
actual computer code of his model. (Bueno
de Mesquita cannot do so because his former
firm owns the actual code, but he counters
that he has outlined the math behind his
model in enough academic papers and books
for anyone to replicate something close to his
work.)
At first BDM (1997) appears to offer the most
promise in elucidating the model, however first
impressions prove misleading. Significant errors and
obfuscations become apparent to anyone who tries to
replicate the model and results from this and later
works. In the following, we carefully navigate and
interpret earlier works to derive a working model
and agent software that reproduces his published
results to an adequate level of accuracy.
2 EVOLUTION OF THE MODEL
BDM’s predictions depend on two parts. First, his
18
Scholz J., Calbert G. and Smith G..
UNRAVELLING BUENO DE MESQUITA’S GROUP DECISION MODEL .
DOI: 10.5220/0003121500180030
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 18-30
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

method of data collection and interpretation from
human subjects; second, the computational model
which he applies to that data.
The first part is significant, but has not been
described by BDM in the open literature and so
evades current interpretation or analysis. The second
part, the computational model we examine further.
The model deals with a single ‘issue’
decomposed into a metric scale, with ‘position’
values (x) corresponding to states of the issue. BDM
illustrates, “The term x
i
represents each nation’s
preferred date, measured in years, by which
emission standards should be applied to medium-
sized automobiles as revealed at the outset of
discussions on the issue.” (BDM, 1994, p.77). We
will continue with this example later in the results
section. A number of ‘actors’ (i=1,2,…,n) exist, each
of which hold a single ‘position’ (x
i
) with regard to
the issue, represented by their assignment to a
location.
Each ‘actor’ is also considered to possess some
‘capability’ (c
i
) with respect to the ‘issue’.
‘Capability’ is sometimes interchangeably referred
to as ‘power’ or ‘resources’ by BDM. Like
‘position’, ‘capability’ is given a value on a metric
scale. This value represents an actor’s level of
influence with regard to the issue.
Lastly, each ‘actor’ is also considered to possess
some ‘salience’ (s
i
) with respect to the ‘issue’.
‘Salience’ is sometimes interchangeably referred to
as ‘importance’, ‘priority’, ‘attention’ by BDM. Like
‘position’ and ‘capability’, ‘salience’ is given a
value on a metric scale. This value represents an
actor’s level of energy with regard to the issue.
Table 1 from BDM (1994, p. 78) illustrates.
Table 1: Example input data for the computational model.
The issue is ‘the date (years) of introduction of emission
standards for medium-sized automobiles’.
Actor (
i
) Capabilit
y
(c
i
)
Position
(x
i
)
Salience
(s
i
)
N
etherlands 0.08 4 80
Belgiu
m
0.08 7 40
Luxembour
g
0.03 4 20
German
y
0.16 4 80
France 0.16 10 60
Ital
y
0.16 10 60
UK 0.16 10 90
Irelan
d
0.05 7 10
Denmar
k
0.05 4 100
Greece 0.08 7 70
BDM’s model decomposes the social fabric into
pairwise ‘contests’ between actors with support or
otherwise of third-party alliances. Based on actor i’s
perception of expected utility, actor i considers
whether or not to challenge each other actor j, in an
attempt to convince them to adopt i’s position. The
expected utility includes an assessment of the level
of third-party support for actor i’s challenge. If actor
i’s expected utility of challenging actor j versus not
challenging is greater than zero, actor i will
challenge actor j, otherwise it will not. This model of
mind or agency is confrontational and wholly self-
interested.
Not surprisingly, BDM has adapted the model
over the years. So it is necessary to clearly identify
which version we are using when considering its
form and results.
BDM (1980) provides the earliest form, which is
repeated in BDM (1981). The notation is later
revised in BDM (1985), and includes a modification
to include a risk exponent; however the basic
expected utility calculations remain the same from
1980 to 1985. We are readily familiar with the
expected value of a random variable Z, with various
states Z
w
each with probability P
w
of occurring as:
w
ww
ZPzE
Expected utility follows the same structure in
that the utilities of different contest outcomes are
estimated along with the associated probabilities.
An apparent motivation for BDM’s expected
utility model was predicting the outbreak of war as
per BDM (1981). It is thus not surprising to find a
confrontational mentality to the basic form of the
model. BDM considers an actor i to choose to
‘challenge’ a rival or opponent actor j. Thereby the
expected utility for i to challenge j is:
fiisii
c
i
UPUPUE 1
Where U
si
refers to the utility for actor i if it
succeeds and U
fi
is the utility for actor i if it fails.
BDM (1985, p. 158) extends this with a third
term relating to the third-party contribution to i’s
expected utility (using BDM’s notation):
jik
i
kj
i
kijkik
i
fi
i
i
si
i
c
ij
i
UUPP
UPUPUE
,
))(1(
1
(1)
If actor i does not challenge j, i stays at the same
position and j may either remain where it is (status
quo) or j may move to a different position. If j
moves, the utility of the outcome may prove either
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
19

better for i or worse for i. The expected utility for i
not challenging is then, BDM (1985, p.158):
i
wi
i
bi
i
bi
i
bi
i
qi
i
qi
i
qi
nc
ij
i
UQUQQ
UQUE
11
(2)
Where Q
q
refers to the probability of status quo and
Q
b
refers to a switch (value either 1 or 0) depending
on whether the outcome was better or worse. These
and other issues will be explained fully later.
The full form of the expected utility difference
combines (1) and (2):
nc
ij
i
c
ij
i
ij
i
UEUEUE
(3)
In BDM and Lalman (1986) a problem with the
following term in (1) is identified:
,
(1)()
iii
ij ik jk ki kj
m
kij
EU P P U U
(4)
The problem is described in BDM and Lalman
(1986):
Because of the manner in which third parties
are treated in earlier studies (Bueno De
Mesquita, 1981, 1985), the operational
estimate of expected utility values for any
decision maker could vary between (2N-2)
and –(2N-2), where N is the total number of
nations in the relevant international system.
Variations in the size of the international
community, then, affected the possible range
of values in the expected utility models set
out earlier. This is a serious shortcoming in
that it makes comparison of a single nation’s
utility scores in different years difficult. …
The new formulation fixes the range of
values, irrespective of system size, in a
theoretically meaningful way. (p. 1119)
BDM’s proposed solution involves removing the
term (4) from (1) and incorporating a more complex
form of calculation of the probability P
i
. In BDM
(1985, p.161) the probability
i
P refers to “P
i
= i’s
probability of succeeding in a bilateral contest with
j”.
From 1986 onwards, the definition of the
probability is changed to account for multilateral
contributions to the contest between i and j. The new
form is denoted
i
i
P . This will be defined later.
The form of the expected utilities as stated in
BDM and Lalman (1986, p. 1118) are:
nc
ij
i
c
ij
i
ij
i
UEUEUE
(5)
i
sij
i
fi
i
i
i
si
i
ij
c
ij
i
Us
UPUPsUE
1
1
(6)
i
wi
i
bi
i
sq
nc
ij
i
UTTUQ
QUUE
11
(7)
The notable change is the inclusion of salience s
j
and
an extra term in the expected utility for challenge.
Otherwise, notation changes are minimal.
This latter structure remains throughout BDM
(1994, 1997, and 2002). In BDM (2009b) a new
structure of model is announced, however we do not
consider this new model further. As a result of the
multi-lateral scaling issue with the model in its pre-
1986 form, we focus on the model structure and
results for 1986 and later, using the form from
equations 5, 6 and 7.
3 UTILITIES
BDM (1997, p.242-243) uses equations (5), (6) and
(7) though with different notation. The probability of
status quo might be determined in a number of ways,
however, a value of Q=1.0 is assumed in BDM
(1985, p.161), corresponding to a stoic opposition
and a value of Q=0.5 is assumed in both BDM and
Lalman (1986, p.1122) and BDM (2009a, p.5),
corresponding to a maximally uncertain outcome of
whether the actor j will move or stay in position. No
explicit value for Q is specified in other papers.
3.1 Base Utilities
To find the expected utility, we need to calculate the
basic utilities:
i
sq
i
wi
i
bi
i
fi
i
si
UUUUU ,,,,
(8)
These utilities are a function of the policy position of
actors, x
i
and x
j
. BDM (1997, p.264) tells us that “…
i’s utility for
k
x
,
k
i
xu
, is a decreasing function of
the distance between the proposal and i’s preferred
resolution, so that
*
Ikk
i
xxfxu
. ”
(9)
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
20

The notation
j
i
xu
is not the same as that used in (8),
so some transformation is probably required. Thus
we interpret (9) as the general class of model only. It
is worth pointing out that a specific class is stated in
BDM (1997, p.245):
i
r
jij
i
xxxu
*
1
(10)
However, (10) is inconsistent with the more detailed
earlier explanations, as the following will now
reveal.
One clue to the utility calculations is given in
BDM (1994):
Should i succeed, then i will derive the utility
associated with convincing j to switch from
its current policy stance to that supported by
i. This is denoted by
dxu
j
i
|
, which equals
)(
ji
i
xxu
. Should i fail, then it confronts
the prospect of having to abandon its
objectives in favour of those pursued by j,
denoted by
).(|
ij
i
j
i
xxudxu
(p. 84)
Once again, BDM introduces additional notation
)(
ji
i
xxu
and
)(
ij
i
xxu
which remains
undefined. However, BDM (1985, p.158) gives
utility for i’s success which is of the form of a
difference between positions i and j:
i
r
i
ij
i
ii
i
si
UU
U
4
2
42
(11)
Also, the utility for i’s failure, which is of the form
of a difference between positions j and i:
i
r
i
ii
i
ij
i
fi
UU
U
4
2
42
(12)
Noting also in BDM (1985):
The reason for the transformations by 2’s and
4’s is to preserve the original scale of
numbers while avoiding the generation of
imaginary numbers. Because r
i
can be less
than 1.0, the absence of transformations
would mean that for negative values of, for
instance U
fi
, no real root would exist. This
problem is eliminated with the introduction
of these transformations. (p. 158)
i
ii
U and
i
ij
U are defined by BDM (1985):
With
i
ii
U being equal to the value i attaches
to his own policy portfolio (Both
ii
U and
jj
U are assumed to equal 1.0, with
ij
U and
ji
U ranging between possible values of 1.0
and -1.0), and with
i
ij
U being equal to the
value i attaches to j’s policies as a function of
their similarity to the policies of i. (p. 158)
Thus,
1
j
jj
j
ii
i
jj
i
ii
UUUU
(13)
And to satisfy the stated range requirement we
propose,
minmax
21
xx
xx
UU
ji
i
ji
i
ij
(14)
Equation (14) is consistent with the statement and
equation at (9). Note that -1≤
i
ii
U
≤1. Where,
x
max
−x
min
is the range of positions. Note the
maximum value of +1 occurs when policy positions
of i and j coincide and is at its minimum of -1 when
the positions are maximally separated.
Summarising, so far we have now accounted for
(8) parts a and b, which simplify to:
i
r
ji
i
si
xx
xx
U
minmax
5.05.042
(15)
i
r
ji
i
fi
xx
xx
U
minmax
5.05.042
(16)
Note the ranges
2)5.0(42
i
si
r
U
i
and
i
r
i
fi
U )5.0(422
are consistent with the
diagram in BDM (1985, p.159).
BDM (1985) does not explicitly define
i
bi
U
or
i
wi
U
, however, we are given in BDM (1985, p.158):
0
24 2 4
i
r
iiiii
qi ii ij ii ij
tn t
UUUUU
(17)
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
21
The subscripts t0 and tn are not defined, but in
BDM (1981, p.48) these correspond to before and
after j’s policy change, respectively. The utility
subscript q is usually signifies status quo, but we
believe this is an error in (17) and should instead
refer to j making a policy change (or move) which
gains or betters the situation for i. We are led to
believe this by BDM (1981, p.47-48):
0t
i
ij
i
ii
UU
=i’s perception of what may be
gained by succeeding in a bilateral conflict
with j…
0t
i
ii
i
ij
UU
= i’s perception of what
may be lost by failing in a bilateral conflict
with j…
So we adopt the subscript, b indicating ‘better’
consistent with (8). Furthermore, we note a problem
with scaling for (17), as it will become undefined
(negative number raised to a power less than 1.0).
Thus, corrections are also required to realign scaling.
The result is as follows:
i
r
t
i
ij
i
ii
tn
i
ij
i
ii
i
bi
UUUU
U
8
4
42
0
(18)
Similarly we expect that j’s movement may
potentially result in a worse condition for i:
i
r
t
i
ii
i
ij
tn
i
ii
i
ij
i
wi
UUUU
U
8
4
42
0
(19)
Note this adjusted scaling ensures
2)5.0(42
bi
r
U
i
and
i
r
wi
U )5.0(422
.
We are given a clue that some relation to the
median voter position is important by
“
]||[ dxuanddxu
j
i
j
i
are approximated by
comparing the value actor i attaches to the current
median voter prediction to the value i attaches to the
median anticipated if i accepts j’s preferred
outcome.” (BDM 1997, p. 248)
BDM (2009a) expresses this most clearly:
… they are anticipated to move towards the
median voter position if they make an
uncoerced move. This means that if B lies on
the opposite side of the median voter from A,
then A anticipates that if B moves
(probability=0.5), then B will move in such a
way as to come closer to the policy outcome
A supports and so A’s welfare will improve
without A having to exert any effort. If B lies
between the median voter position and A,
then whether A’s welfare improves or
worsens depends on how far B is expected to
move compared to A. The same is true if A
lies between B and the median. (p. 6)
We interpret this to mean that for no challenge
(uncoerced), and B (or j) moves, that A (or i)
expects B (or j) will move to the median position.
The cases are illustrated in figures 1 to 4.
i
j
j
i
Figure 1: Case 1:
between i and j
utility for i gets
better as a result of
j moving.
i
j
j
i
Figure 2: Case 2:
j between i and
utility for i gets worse
as a result of
j moving.
j
i
ij
Figure 3: Case 3A:
i between j and
utility for i gets
better as a result of
j moving.
ji
i
j
Figure 4: Case 3B:
i between j and
utility for i gets
worse as a result of
j moving.
For any of these cases then we expect,
minmax
0
21
xx
xx
U
ji
t
i
ij
(20)
minmax
21
xx
x
U
i
tn
i
ij
(21)
Substituting (20) and (21) into (18) yields:
i
r
jii
i
bi
xx
xxx
U
minmax
25.05.042
(22)
Substituting (20) and (21) into (19) yields:
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
22

i
r
jii
i
wi
xx
xxx
U
minmax
25.05.042
(23)
We note further, that these utilities must be applied
in the appropriate cases. Thus if case 1 is true, then
the probability of i’s utility improving is 1.0 and by
implication the probability of i’s utility worsening is
0.0. We believe this defines the probability T in
equation (7), though no known publication by the
author states this explicitly. So, cases 1 and 3A
correspond to T=1 and cases 2 and 3B correspond to
T=0. This helps explain the description in BDM
(1986, p. 1122).
Lastly, for the situation of no change in policy
(status quo) i does not challenge and j does not
move, BDM (1985, p.158) defines:
i
i
r
r
i
sq
U 5.042
4
)02(
42
(24)
We expect this corresponds to (8) part e.
To determine the calculations for actor j, BDM
(1985) notes:
Of course, the
j
f
j
s
UU ,
and
j
q
U
terms (with
appropriate superscripts) are defined
analogously. These terms vary as a function
of whose estimate of expected utility is being
calculated (i.e., who is the superscripted
actor) by varying the risk exponent, so that
for expected utility equations with a j
superscript, j’s risk taking propensity is used
to estimate what j perceives to be the value of
success, failure, or no challenge for i in
accordance with the equations delineated
below. (p. 158)
Thus, the two main equations become:
11
(1 ) (1 )
iiiii i
ij j i si i fi j si
iii
s
qbiwi
EU s PU PU sU
QU Q TU T U
(25a)
11
(1 ) (1 )
jjjjjj
ji j j sj j fj j sj
jjj
sq bj wj
E
UsPU PU sU
QU Q TU T U
(25b)
3.2 The Median Voter Position
In the previous section, it became clear that the
“median voter position” must be determined in order
to calculate the utility terms in (22) and (23).
BDM defines comparative votes in direct propor-
tion to utility difference, capability and salience. The
votes ‘cast’ by agent i in comparing positions
j
x
and
k
x
is given as BDM (1997, p.239):
k
i
j
i
iikj
jk
i
xuxuscxxv ,|
(26)
We emphasise, that these votes cast to k may
indeed be negative, if for example, agent i prefers j
to
.k To map this notation to that used previously,
we interpret:
ijj
i
Uxu
&
ikk
i
Uxu
(27)
Using (14) we get:
minmax
2,|
xx
xxxx
scxxv
jiki
iikj
jk
i
(28)
According to BDM (1997):
The prospect that a proposal will succeed is
assumed to depend on how much support can
be mustered in its favour as compared with
the feasible alternatives. This is calculated as
the sum of “votes” across all actors in
comparison between x
j
and x
k
. (p. 240)
n
i
jk
i
jk
vv
1
(29)
In general, this pairwise determination is termed a
Condorcet Method of voting. A Condorcet winner is
the candidate whom voters prefer to each other
candidate, when compared to them one at a time.
Black’s Median Voter theory now comes into
play, so “the decision adopted by the committee
becomes determinant as soon as the position of the
one optimum – which we can refer to conveniently
enough as the median optimum – is given.” (Black,
1948).
That is, in a majority election where a voter’s
attitude is represented as a point in one dimension, if
all voters vote for a candidate closest to their own
preference and there are only two candidates, then if
the candidates want to maximise their votes they
should commit to the policy attitude preferred by the
median voter.
The median voter’s ideal attitude is always a
Condorcet winner (Congleton, 2003). Thus the
median voter attitude index and the number of votes
at the median attitude may be determined.
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
23
4 ALLIANCE PROBABILITY
The probabilities of equations (25) are determined
by the bilateral alliances. BDM determines these
probabilities by combining across all pairs, an
assessment of ‘who is with me’ (positive valued
vote) versus ‘who is against me’ (negative valued
vote) and normalising. BDM (1997, p.244) states the
estimator as:
n
k
ij
k
xuxuk
ij
k
i
vvP
j
k
i
k
1|
(30)
When more agents are ‘for’ than ‘against’, this raises
the probability of winning the bilateral contest. As
per previous derivation of votes, substitute and
expand (31):
n
k
ikjkkk
ifk
ikjkkk
i
xxxxsc
xxxxsc
P
i
1
0arg
)(
)(
(31)
5 RISK PROPENSITY
As seen in the previous section, utility calculations
involve a risk exponent. This risk exponent is in turn
derived from the expected utility. BDM (1985,
p.157) is first to describe the basis for risk
calculation,
I define each nation’s security level as
ij
ji
UE )( . The greater the sum, the more
utility i believes its adversaries expect to
derive from challenging i. … as this sum
decreases, i’s relative security increases, so
that i is assumed to have adopted safe
policies ...
BDM (1985, p.157) goes on to define:
max min
max min
2() () ()
() ()
ji ji ji
i
ji ji
EU EU EU
R
EU EU
(32)
Note that BDM (1997, p.247) reverses the subscripts
of the above, which is inconsistent with his
conceptual basis of security. Further, BDM
(1997,p.247) provides an inconsistent transformation
formula which would not accommodate the range
11
i
R
. Thus, we choose the earlier conversi-
on formula from BDM (1985, p.157):
3/1
3/1
i
i
i
R
R
r
(33)
The purpose of the formula according to BDM
(1985, p.157) is to ensure that r
i
ranges between 0.5
and 2, noting that the divisor of 3 appears arbitrary,
but effects curvature. Equation (33) is illustrated in
figure 5.
0
0.5
1
1.5
2
‐1
‐0.6
‐0.2 0
0.2
0.6
1
r
i
R
i
Figure 5: Scaling conversion formula.
The following equation (34), expresses (32)
more precisely:
1, 1, 1,
1, 1,
2()max ()min ()
max ( ) min ( )
nn n
ii i
ji ji ji
i
i
jji jji jji
i
nn
ii
ji ji
i
i
jji jji
EU EU EU
R
EU EU
(34)
We still need to know, however, how to calculate the
expected utilities in (25), which use a modified
notation. BDM (1985) describes:
Thus, the risk terms are calculated by
manipulating the alliance portfolios used as
the policy indicator through simulation to
locate the best and worse portfolios for any
given nation, where the best and worst are
defined in terms of the sum of expected
utilities of all others vis-à-vis the nation in
question under the assumption that utilities
are strictly a function of similarities in
alliance commitments. (Note: That is,
temporarily applying the expected utility
equations (without risk or uncertainty taken
into account) as developed in The War Trap,
I identify the worst and best case alliance
strategy for each nation each year, using the
original, linear utility functions to define the
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
24

range of possible expected gains or losses for
each nation. These, then, are utilized to
measure risk propensities and thereby to
introduce curvature into the utility functions.)
(p. 167-168)
This implies a process to first determine the
expected utilities of equations (25) using r
i
=1, then
apply (34) and (33) to estimate r
i
and lastly apply the
r
i
estimates to re-estimate the expected utilities of
equations (25).
6 DECISION
6.1 Offer Categories
The expected utilities
ij
i
UE
and
ji
j
UE
are used
to classify the ‘offers’ between all actor pairs into
categories according to potential outcomes as
illustrated in figure 6. An actor may expect to
conflict, compromise, capitulate, or stalemate with
another. Unfortunately no single publication by
BDM explains how to quantify these.
Confrontation +
j moves to i
Confrontation -
i moves to j
i’s Expected
Utility
j’
s
E
xpected Utility
Compromise +
j moves part
way to i
Compromise -
i moves part
way to j
Compel -
i moves to j
CONFLICT
CONFLICT
STALEMATE
STALEMATE
COMPROMISE
COMPROMISE
COMPROMISE
COMPROMISE
CAPITULATE
CAPITULATE
CAPITULATE
CAPITULATE
Status Quo
i stays put
Compel +
j moves to i
ij
i
UE
ji
j
UE
Figure 6: Classifying the outcome of challenges according
to
i’s viewpoint.
Conflict. Actors i and j conflict if
0)(
ij
i
UE
and
0)(
ji
j
UE
. So “If both i and j believe that they
have the upper hand in the relationship, then conflict
is likely and that conflict has an uncertain outcome.”
BDM (1997, p.244)
BDM (1984, p. 230) labels for the
“Confrontation-” octant, “Challenger Favored” and
for the “Confrontation+” octant “Favoring Focal
Group”. We interpret this to mean i moves to j and j
moves to i respectively, as shown in figure 6.
Compromise. Actor i has the upper hand if
0)(
ij
i
UE
,
0)(
ji
j
UE
and
)()(
ji
j
ij
i
UEUE
.
Actor j has the upper hand if
0)(
ij
i
UE
,
0)(
ji
j
UE
and
)()(
ji
j
ij
i
UEUE
.
BDM (1997) describes:
… both players agree that i has the upper
hand. In this instance, j is expected to be
willing to offer concessions to i, although the
concessions are not likely to be as large as
what i would like. The likely resolution of
their exchange is a compromise reflecting the
weighted average of i’s expectation and j’s.
(p. 243-244)
However, the weighted average is not clear. BDM
(1994) states (presumably with regard to i having the
‘upper hand’):
… the concession is assumed to equal the
distance on R
a
between x
i
and x
j
multiplied by
the ratio of the absolute value of j’s expected
utility to i’s expected utility. This treats the
compromise as the weighted average of the
perceived enforceability of the demand… (p.
96)
We might interpret this literally as:
)(
)(
ˆ
ij
i
ji
j
ji
UE
UE
xxx
(35)
Noting this relates only to the octant labeled
“Compromise +” in figure 6. Considering the
boundary conditions in this octant, if
)()(
ji
j
ij
i
UEUE
then
0
ˆ
x
and actor j does not
move from x
j
and if
)()(
ji
j
ij
i
UEUE
then
1
ˆ
x
and actor j moves from x
j
to x
i
. For the octant
labelled “Compromise -” we use:
)(
)(
ˆ
ji
j
ij
i
ji
UE
UE
xxx
(36)
Acquiescence and Stalemate. The states for
acquiescence and stalemate are illustrated in figure 6
and require no further explanation.
6.2 Offer Selection
Given that each actor has chosen who to challenge
and to remain silent for those not to be challenged,
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
25
then each actor will have received ‘challenge offers’
from other actors. How does an actor come to a
decision on it which challenge offer it should
accept? BDM (1997) elucidates:
Each player would like to choose the best
offer made to it and each proposer enforces
its bid to the extent that it can. Those better
able to enforce their wishes than others can
make their proposals stick. Given equally
enforceable proposals, players move the least
that they can. … When the players finish
sorting out their choices among proposals,
each shifts to the position contained in the
proposal it accepted. (p. 251-252)
If all offers are equally enforceable, we would
propose to order these according to an actor’s
preferred choice as follows, so that actor i moves
‘the least that it can’. Thus, summarising the order
of decision choice for actor i is as follows:
1. Actor i conflicts
with actor j and actor j (or with
some chance actor i) acquiesces
.
2. Actor i compromises
to actor j. Actor i loses
some ground.
3. Actor i acquiesces
to actor j. Actor i loses most
ground.
4. Actor i stalemate
with actor j. Actor i status quo.
Thus, for example if actor i is in conflict with
several other actors, each of which have greater
expected utility than i, then the agent will need to
concede to the one that allows i to move the least.
If all offers are not equally enforceable, then we
might expect an actor to be more likely to concede
to the most powerful actor. Thus, in the prior
example, actor i concedes to the actor with highest
expected utility.
7 RESULTS
BDM (1994) provides an example. The data for this
was introduced in table 1. BDM (1994) provides
three graphs of results. These compare expected
utility for Belgium versus the others, France versus
the others and the Netherlands versus the others.
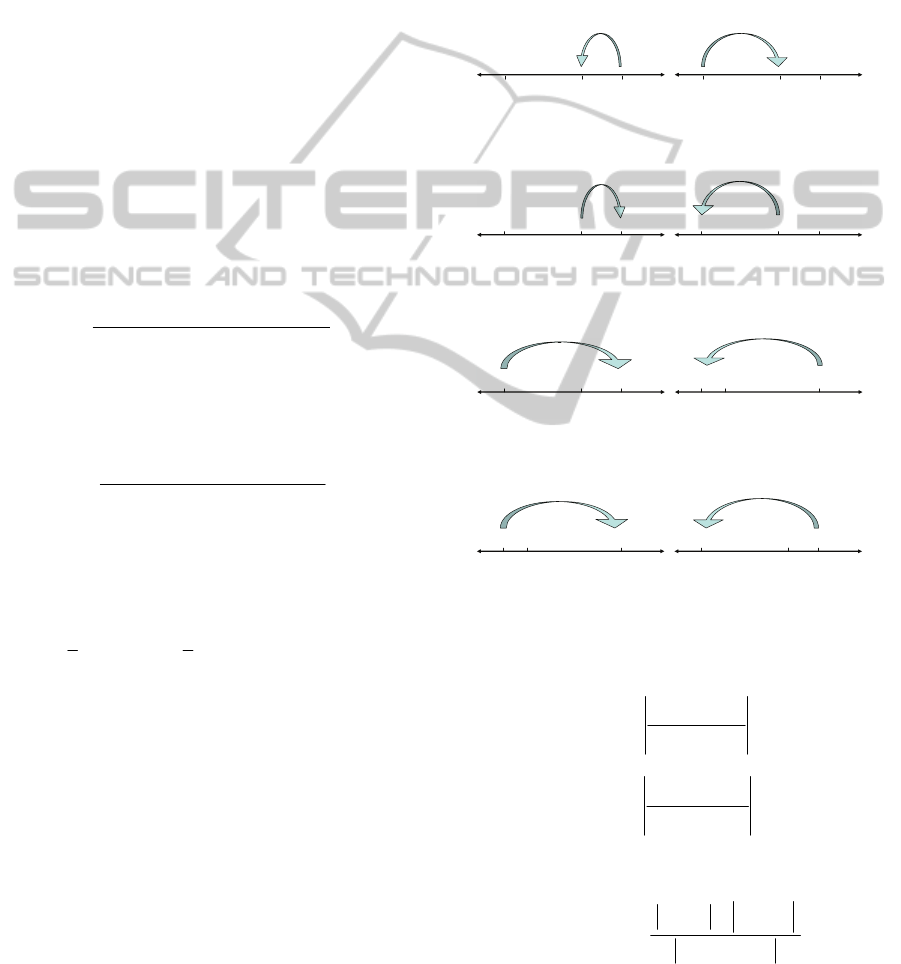
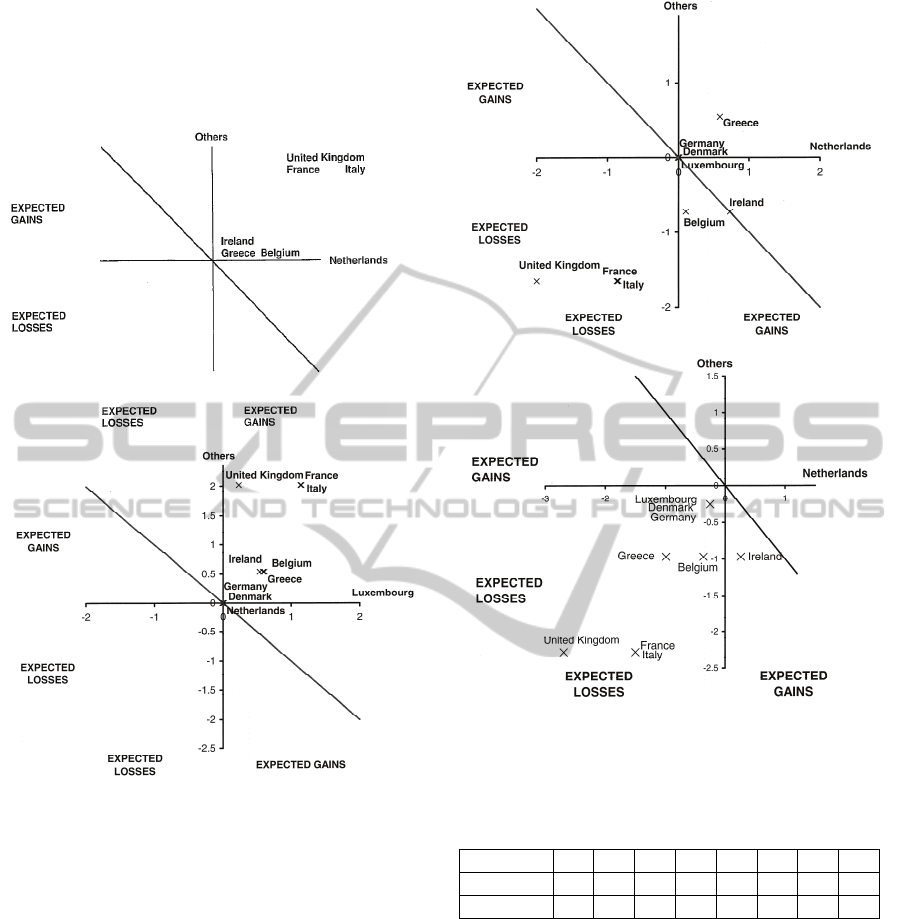
Figures 7 and 8 compare the result using our
interpretation of the algorithm as given in section 6,
compared directly with the results published in
BDM (1994, p.91). No value for Q was given. We
chose Q=1.0.
Figure 7: Comparison of results for BDM (1994) (top) and
our interpretation (bottom), view from Belgium.
Note that some countries are not shown on
BDM’s graphs. In figure 7, our expected utility
results for Ireland and Greece were (0,0) and in
figure 8, UK and Italy were at (0,0).
As a result of the fact that BDM does not
explicitly plot the point locus of the expected
utilities, we can only reasonably assume the
quadrants where the names are labelled corresponds
to the location of each locus. The correspondence of
our results to this level of accuracy (within a
quadrant) is 100%. We note that if the expected
utilities were derived randomly, the probability of
getting any one of these points located in the correct
quadrant is one in four. In order to get all nine
results in the correct quadrants for any one graph of
the two graphs above would constitute a probability
of (1/4)
9
~ 4x 10
-6
. We therefore assert that BDM’s
results have effectively been reproduced.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
26
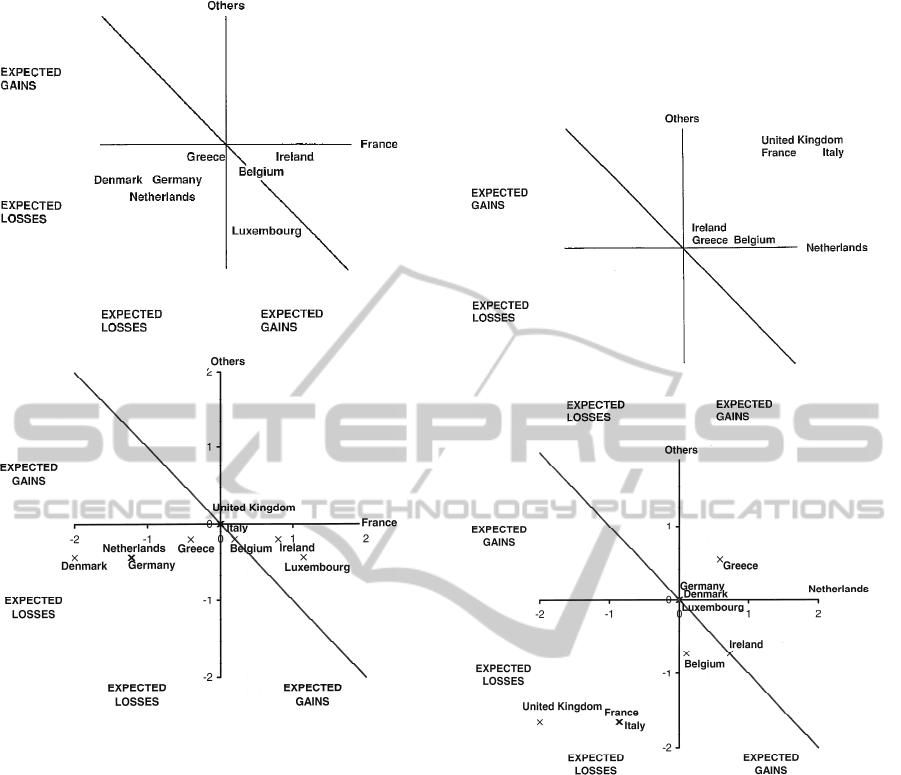
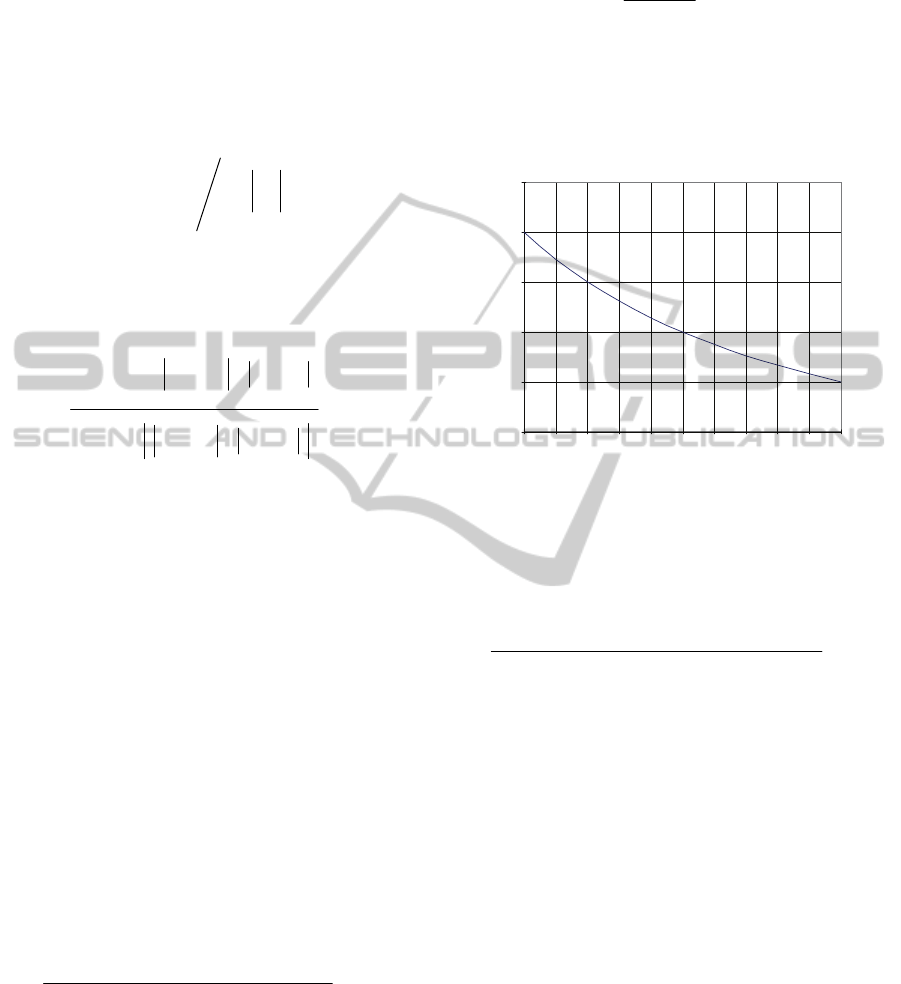
Figure 8: Comparison of results for BDM (1994) (top) and
our interpretation (bottom), view from France.
We came across an issue with trying to
reproduce the result given by BDM for the
Netherlands as compared in figure 9. We assert that
the result published by BDM was in error. Our result
showing ‘Others’ as
ji
j
UE
against
ji
i
UE
for
i=Luxembourg is compared with BDM’s quoted
result in figure 10. This shows 100%
correspondence in terms of quadrant accuracy as for
the previous two results.
BDM (1994) summarises the final result:
The dominant outcome would be, as
indicated above, a lag of 8.35 years.
However, if the participants were prepared to
bear the costs of slightly prolonged
negotiations, then the model’s predicted
dominant outcome rises to 9.05 years and
stabilizes at that point. … The actual
resolution was for a delay of 8.833 years.
(p.98)
We found the median voter position at the end of
the first round to be 8.4 years. At the end of the
second, third, fourth and fifth rounds the median
voter position was for each 9.9 years.
Figure 9: Comparison of results for BDM (1994) (top) and
our interpretation (below), view from Netherlands.
8 DISCUSSION
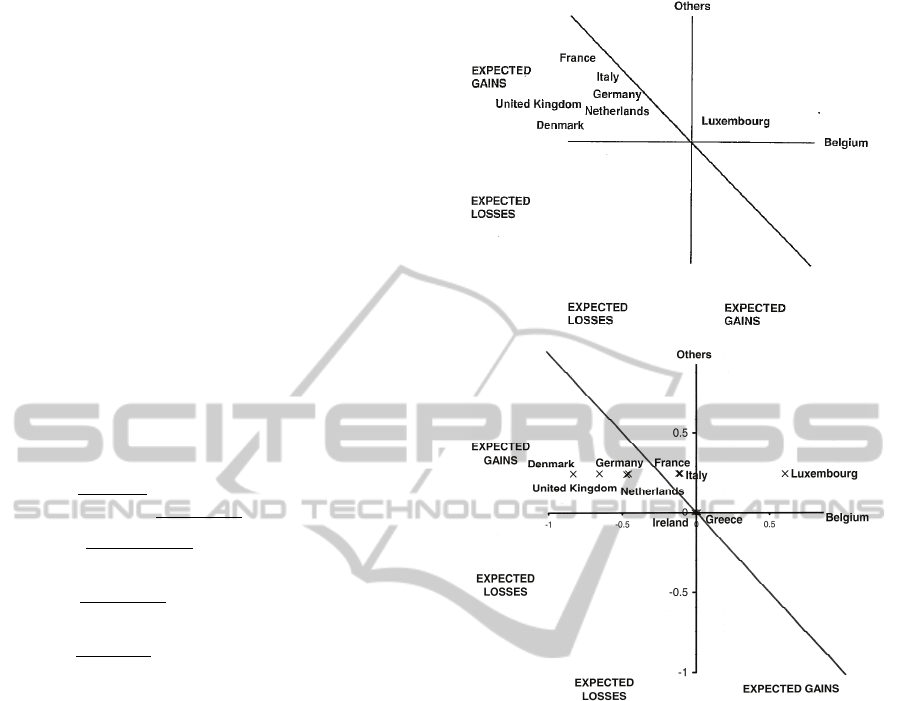
As identified earlier, we chose Q=1.0 to reproduce
the results above. We observed that a value of Q=0.5
produces very different results. The following figure
11 provides an illustrative example.
In figure 11, the positions of Greece and
Belgium change entire quadrants if Q=1 or Q=0.5 is
chosen.
Recalling that Q relates to the probability of a
status quo and is an arbitrary parameter, it is not
desirable for results to be so sensitive.
We examined the applicability of the
interpretation to other examples from later papers.
Despite the fact that BDM (1994) and BDM (1997)
differ only in the detailed example used, it is
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
27
perplexing that we were unable to reproduce the
results from the 1997 paper. Indeed attempts to
apply this algorithm (using either Q=0.5 or Q=1.0)
to the 1997 “Sultan” problem yielded wildly
different results to those published.
Figure 10: Comparison of results for BDM (1994) ‘view
from Netherlands’ and our interpretation, view from
Luxembourg.
Further insight on the evolution of the median
voter position over rounds is also warranted. This is
shown in table 2.
Table 2 shows that the median appears to
stabilise, but then continues to change. Calculation
of the mean voter position provides insight. The
coarseness of the median voter position becomes
evident. Indeed given the fact that the “compromise”
state allows for intermediate valued positions (as per
equation 36) it is surprising that BDM would want to
continue with median over mean values. In general
the results do not stabilise. There is no reason from
examining the algorithm to expect that they should.
Figure 11: Example for Netherlands comparing results
using
Q=1.0 (top) and Q=0.5 (bottom).
Table 2: Evolution of the median and mean voter positions
for ‘the date of introduction of emission standards for
medium-sized automobiles’ problem in BDM (1994).
Round 1 2 3 4 5 6 7 8
Median 8.4 9.9 9.9 9.9 9.9 7.4 8.8 9.6
Mean 7.4 7.5 7.6 7.3 7.3 7.4 7.5 7.6
9 CONCLUSIONS
The algorithm outlined (and summarised in the
Appendix) has for the first time exposed and
provided independent means of replicating the
results of BDM’s computational model. This opens
BDM’s model, method and claims to scientific
discussion.
The correctness of the interpretation was
illustrated using the example from BDM (1994). We
note the chance of replicating to this level of
accuracy by random selection would be much less
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
28

than one in one million. This fulfils Bueno De
Mesquita’s own prediction that enough material is
available so that “anyone (may) replicate something
close to his work”!
Concerns with regard to the model’s sensitivity
and convergence have been identified.
Given these concerns, we conclude that adoption
of BDM’s model for agent development would be
premature at this time.
REFERENCES
Black, D. (1948). On the Rationale of Group Decision-
making.
Political Economy 56, No 1, Feb: 23-34.
Congleton, R. D. (2003). The Median Voter Model.
The
Encyclopedia of Public Choice.
Kluwer Academic
Press: 382-386.
Bueno De Mesquita, B. B. (1980). An Expected Utility
Theory of International Conflict.
The American
Political Science Review
, Vol. 74, No. 4 (Dec), pp.
917-931.
Bueno De Mesquita, B. B. (1981). The War Trap. Yale,
CT: Yale University Press.
Bueno De Mesquita, B. B. (1984). Forecasting Policy
Decisions: An Expected Utility Approach to Post-
Khomeini Iran, The American Political Science
Review
, Vol. 17, No. 2, pp. 226-236.
Bueno De Mesquita, B. B. (1985). The War Trap
Revisited: A Revised Expected Utility Model.
American Political Science Review 79, No 1, 156-177.
Bueno De Mesquita, B.B. and Lalman, D. (1986). Reason
and War, The American Political Science Review, Vol.
80, No. 4, (Dec), pp. 1113-1129.
Bueno De Mesquita, B. B. (1994). Political Forecasting:
An Expected Utility Method,
European Community
Decision Making
, Yale University Press, Stockman, F.
(ed.), Chapter 4, pp 71-104.
Bueno De Mesquita, B. B. (1997). A Decision Making
Model: Its Structure and Form.
International
Interactions
23: No 3-4 235-266.
Bueno De Mesquita, B. B. (2002).
Predicting Politics,
Ohio State University Press.
Bueno De Mesquita, B. B. (2009a).
A New Model for
Predicting Policy Choices: Preliminary Tests
, 50
th
Meeting of the International Studies Association, New
York, Feb 15-18.
Bueno De Mesquita, B. B. (2009b).
The Predictioneer’s
Game
(1
st
ed.). New York: Random House.
Kollman, K, Miller, J. H. and Page, S.E. eds (2010)
Computational models in political economy. MIT
Press.
APPENDIX
The following summarises the full procedure.
1. Given i=1,2,…,n actors, initial positions for each actor
x
i
(t=0), c
i
, s
i
and number of rounds=
.
2. Let r
i
=1
3. Calculate the pairwise votes:
n
i
jiki
ii
jk
xx
xxxx
scv
1
minmax
Then find the maximum value which corresponds to
the Condorcet winner position or median =
.
4. Calculate basic utilities,
i
r
ji
i
si
xx
xx
U
minmax
5.05.042
i
r
ji
i
fi
xx
xx
U
minmax
5.05.042
i
r
jii
i
bi
xx
xxx
U
minmax
25.05.042
i
r
jii
i
wi
xx
xxx
U
minmax
25.05.042
i
r
i
sq
U 5.042
5. Calculate probabilities:
n
k
ikjkkk
ifk
ikjkkk
i
xxxxsc
xxxxsc
P
i
1
0arg
)(
)(
6. Let Q=0.5 (or 1.0).
7. Calculate:
i
wi
i
bi
i
sq
i
sij
i
fi
i
i
i
si
i
ijij
i
UTTUQQU
UsUPUPsUE
)1()1(
11
j
wj
j
bj
j
sq
j
sj
j
j
fj
j
j
j
sj
j
j
jji
j
UTTUQQU
UsUPUPsUE
)1()1(
11
If second pass (used the calculated values of r
i
) then,
go to step 11.
8. Calculate:
n
ijj
ji
i
i
n
ijj
ji
i
i
n
ijj
ji
i
i
n
ijj
ji
i
i
n
ijj
ji
i
i
UEUE
UEUEUE
R
,1,1
,1,1,1
)(min)(max
)(min)(max)(2
UNRAVELLING BUENO DE MESQUITA'S GROUP DECISION MODEL
29

9.
Calculate:
3/1
3/1
i
i
i
R
R
r
10. Go to step 4, using calculated values of r
i
.
11. Determine new position decisions
x, based on rules in
section 5 for octant of
E
ij
(i) vs E
ji
(j).
12. Increment the rounds, t=t+1
13. If t=
then stop.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
30
