MOLECULAR FUZZY INFERENCE ENGINES

Development of Chemical Systems to Process Fuzzy Logic at the Molecular Level

Pier Luigi Gentili

Department of Chemistry, Perugia University, Via Elce di sotto 8, Perugia, Italy

Keywords: Molecular processors, Qubit, Fuzzy sets, Wavefunctions, Fuzzy logic systems, Logistic function.

Abstract: Current Information Technology is pursuing a revolution in the design of computing machines: it is trying

to pass from macroscopic processors miniaturized through top-down approaches, to microscopic processors

made of single molecules assembled through bottom-up approaches. When computations are carried out by

single atoms and molecules, quantum logic can be processed. It is difficult to devise a quantum computer

due to the decoherent effects exerted by the surrounding environment. However, it is still possible to work

out with molecules, by abandoning the lure of quantum logic and processing classical logic. Single

molecules make binary computations, whereas ensembles of molecules can be used to implement either

Boolean logic gates or Fuzzy inference engines. The behaviours of two chemical compounds after photo-

excitation are described as examples of quantum systems whereby Fuzzy logic can be processed by

exploiting the decoherent effects exerted by the surrounding microenvironment.

1 INTRODUCTION

Information Technology is trying to develop systems

capable of processing larger amounts of information

at increasingly high speed and lower power, volume

and price. Current computers are based upon

semiconductor technology and electrical signals.

Their computational power has been growing

exponentially. The pace of their improvement is

epitomized in the empirical Moore’s law, stating that

the number of transistors per chip doubles every

eighteen months (Jurvetson, 2004). Moore’s law has

been obeyed, almost precisely, in the last forty years,

by virtue of the continuous progress in the

miniaturization of computer’s processors.

In current computing machines based upon

classical physics, both Boolean and Fuzzy logic can

be processed. Binary information is recorded in

macroscopic two level systems: i.e., when there is no

electrical current flowing through a wire, it

represents a logical “0”, whereas when there is some

current flowing through, it represents a logical “1”.

These two states form a bit of information. All

Boolean computations are based on logical

manipulation of bits through logic gates acting on

wires representing these bits. On the other hand, the

most effective implementations of Fuzzy logic have

been achieved by the use of analog electronic

circuits that are based on continuously variable

electrical signals. Boolean binary logic has the

peculiarity of manipulating only statements that are

true or false, reducible to strings of zeros and ones.

However, quite often, the available data and

knowledge suffer a certain degree of uncertainty and

imprecision, especially when they are based on

subjective linguistic statements. In all these cases, it

is still possible to process information by

abandoning hard computing, based on binary logic

and crisp systems, and adopting soft computing,

based on Fuzzy logic, neural nets and probabilistic

reasoning (Zadeh, 1994). Fuzzy logic is likely to

play an increasingly important role in the conception

and design of systems whose machine intelligence

quotient is much higher than that of systems

to deal with certain and uncertain information,

objective and subjective knowledge.

Until now, the miniaturization of computer’s

elements has been pursued by the top-down

approach through photolithography and related

techniques. The race towards always smaller

dimensions is now approaching some fundamental

limits, because processors are being made of a few

atoms. Fundamental technological problems arise,

such as current leakage and heat dissipation.

Therefore, an alternative strategy, named as bottom-

205

Gentili P..

MOLECULAR FUZZY INFERENCE ENGINES - Development of Chemical Systems to Process Fuzzy Logic at the Molecular Level.

DOI: 10.5220/0003125102050210

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 205-210

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

up approach (Feynman, 1960), has been put forward

over the last few years. It is based on the idea of

building a computer with its underlying hardware

based on single molecules, self-assembled

supramolecular entities and/or chemical reaction

networks coupled with diffusion processes. The

development of molecular logic gates will allow not

only electrical but also other physical and chemical

inputs and outputs to be exploited. The purpose is to

find out molecular systems whereby not only

Boolean but also Fuzzy logic can be processed.

2 COMPUTING WITH

MOLECULES

Working with single atoms and molecules entails to

deal with the laws of the quantum-mechanics,

therefore quantum computation can also be carried

out. The elementary unit of quantum information is

the qubit or quantum bit (Schumacher, 1995). A

qubit is a quantum system that has two accessible

states, labelled

0 and 1 , and it can exist as

superposition of them; in other words, a qubit (

Ψ )

is a linear combination of

0 and 1 :

1b0aΨ 

(1)

wherein a and b are complex numbers, and a

normalization convention

 ba is generally

adopted. A computer based upon qubits promises to

be immensely powerful because it can be in

multiple states at once. For instance, if it consists of

n unmeasured qubits, it can be in an arbitrary

superposition of up to 2

different states

simultaneously, differently from a classical

computer that can only be in one of the 2

states at

any one time (Bennet, 2000). The superposition can

involve also the quantum states of physically

separated particles, if they are entangled (Plenio,

2007).

The main difficulty in building a quantum

computer comes from the fact that quantum states

must constantly contend with insidious interactions

with their environment triggering loss of coherence.

The superposition state of a qubit, for example

defined in equation (1), collapses by decoherence,

into a single state,

0 or 1 , with probability a

and

, respectively.

Whenever decoherence effects are unavoidable,

the lure of quantum information vanishes. However,

it is, anyway, possible to compute with molecules by

processing crisp logic. Since a qubit,

Ψ , can

collapse into one of two available states,

0 or 1 ,

it seems obvious that just Boolean logic can be

implemented at the molecular level.

The ability of making computation by molecules

resides in their structures and their reactivity (i.e.

affinity). The order, the way the atoms of a molecule

are linked, and their spatial distribution rule the

intra- and inter-molecular interaction capabilities of

the molecule itself, defining its potentiality of

storing, processing and conveying information.

Any molecule or supramolecular assembly that

can exist in two states of different chemical or

physical properties, may be regarded as a potential

logic gate if there exist physical or chemical stimuli

that can change reversibly the state of the system.

Computing with molecules allows multiple inputs

and outputs to be used: not only electrical but also

chemical, optical, mechanical, thermal, magnetic

and other physical ones. The nature of logic gates

that can be implemented depends on the response of

chemical compounds to the physical or chemical

inputs.

When computations are performed through an

ensemble of a huge number of molecules, the

collective response of the chemical system is

continuous on a macroscopic level, although only

discrete processes of Boolean character are involved

at the molecular level. Whenever the macroscopic

input-output relation has sigmoid shape, it has

digital character and is suited to process binary

logic. For this purpose, it is necessary to establish a

threshold value and a logic convention for every

input and output variable. The variables can assume

simply high or low values that become digital 1 or 0,

respectively, in the positive logic convention,

whereas the negative logic convention reverses this

relationship. On the other hand, whenever the output

variable varies smoothly as response of the

continuous variation of the input, their relation has

analog character and can be exploited to process

Fuzzy logic. For this purpose, the entire domain of

each variable, referred to as the universe of

discourse, is divided into different Fuzzy sets whose

shape and position define their membership

functions.

Different technological solutions have been put

forward for the implementation of chemical

computers. They can be grouped in two sets: one

that can be defined as based upon “interfacial

hardware” and the other that is based upon the so-

called “wetware”. In the case of “interfacial

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

206

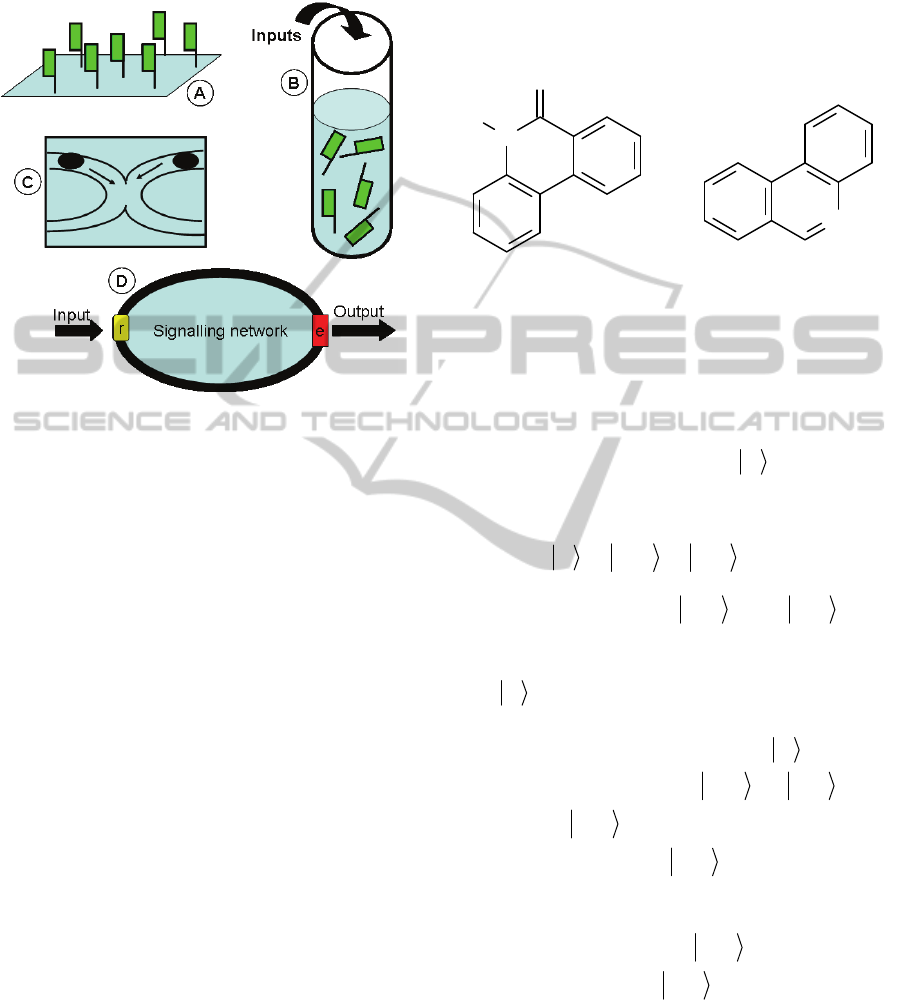
hardware”, the computations are carried out by a

single or an ensemble of molecules anchored to the

surface of a solid phase (see Figure 1 A).

Figure 1: Technological implementations of chemical

computing: (A) interfacial hardware; wetware (B) in a test

tube, (C) through a microfluidic system, and through a (D)

type-cell system wherein “r” stands for receptor and “e”

for effector.

In the case of molecular computing based upon

“wetware”, soups of suitable chemicals process

information through reactions, coupled or not with

diffusion processes. These soups can work inside a

test tube (Figure 1 B) wherein computations are

performed through perturbations coming from the

outside world. Alternatively, the chemical soups can

operate in microfluidic systems (see Figure 1 C)

structurally related with the pattern of the current

electronic microchips: the microfluidic channels are

the wires distributing the information, while logic

operations are processed in the reaction chambers. A

refined way of implementing chemical logic gates

entails emulating the complex molecular signalling

circuits that are active inside a living cell (see Figure

1 D). These circuits consist of (i) receptor units,

sensing the inputs coming from the outside, (ii)

processors, made of reaction-diffusion processes,

and (iii) effectors, unveiling the results of

computation.

3 CHEMICAL PROCESSORS

FOR FUZZY LOGIC

So far many chemical systems have been proposed

as digital logic gates (Szaciłowski, 2008), whereas a

few have been found suited to implement Fuzzy

inference engines. An example of the latter (Gentili,

2007b) is offered by aromatic carbonyl and nitrogen-

heterocyclic compounds (see Figure 2), exhibiting

Proximity effects in their photophysics (Gentili,

2007a).

(a)

(b)

Figure 2: (a) 6(5H)-Phenathridinone, an example of

aromatic carbonyl compound, and (b) phenanthridine, an

example of nitrogen-heterocyclic compound.

The excitation of these compounds by UV-

visible radiation of right frequency triggers the

formation of a quantum state,

 , that is the

superposition of two pure electronic excited states,

as indicated in equation (4):

*,*,







(2)

The two wavefunctions,





and





, are

relative to the electronic (

,*) and (n,*) states,

primarily due to the C=O and C=N chemical groups.

The

 qubit has usually a short lifetime, of the

order of nanoseconds; therefore, it is not suited to

implement quantum computation.

 quickly

collapses to one of its states,









. If it

collapses to





, the molecule can emit light,

whereas if it collapses to





, the molecule does

not fluoresce at all, since it relaxes thermally to the

electronic ground state bypassing the (

,*) state.

The probability of getting





is equal to a

whereas that of getting





is equal to b

. The

coefficients, a and b, depend on the vibronic

coupling between the two close-lying (

,*) and

(n,

*) states (Siebrand, 1980). In planar aromatic

molecules, such as those of Figure 2, the mode that

couples the (

,*) and (n,*) states is a low

frequency out-of-plane bending mode since n and



orbitals are symmetric and antisymmetric with

MOLECULAR FUZZY INFERENCE ENGINES - Development of Chemical Systems to Process Fuzzy Logic at the

Molecular Level

207

respect to reflection through the molecular plane

(Lim, 1986). The wider the energy gap between the

(

,*) and (n,*) states, the weaker the coupling

between them. When the two electronic excited

states couple weakly, the a coefficient of equation

(2) assumes large values. That means the probability

) that



collapses to





is high. If a

large, the observable fluorescence quantum yield,

measured for an ensemble of molecules, results

large.

It is possible to control the extent of the coupling

between the (

,*) and (n,*) states, and hence the

fluorescence quantum yield (



) of an aromatic

carbonyl and nitrogen-heterocyclic compound, by

some environmental conditions, such as the

temperature and the solvent. In fact, high

temperature (T) implies large thermal energy

available to the molecular vibrational motions (in

particular to the low frequency out-of-plane bending

mode, cited above), and hence strong coupling.

Moreover, if the lowest excited state occurs to be

(

,*) in character, the energy gap between the

(

,*) and (n,*) states may increase in going from

aprotic to protic solvents, since the (n,

*) state blue

shifts, whereas the (

,*) state red shifts, under the

influence of hydrogen bonding. In other words, by

choosing solvents with strong hydrogen bonding

donation ability (HBD), it is possible to weaken the

coupling between the two excited states.

An example of the dependence of



on T and

HBD ability of solvent is shown in Figure 3 for

6(5H)-Phenanthridinone. From the 3-D plot of

Figure 3, it is evident that



varies smoothly with T

and HBD ability of the solvent, therefore their

relation is suited to process Fuzzy logic. Fuzzy

Logic Systems (FLS), based upon the photophysics

of 6(5H)-Phenanthridinone, can be implemented.

This is due to the fact that the quantum phenomenon

of superposition, underlying the Proximity effect of

6(5H)-Phenanthridinone, has characteristics

common to the algebra of Fuzzy sets. In fact, the

qubit

 , produced by absorption of an UV

photon, can be conceived as a Fuzzy variable

divided in two Fuzzy sets:





and





.  ,

which is a superposition of





and





belongs to both Fuzzy sets, at the same time. The

degree of membership of

 to the





Fuzzy

set is a

, whereas the degree of membership to the

other





Fuzzy set is b

. The degree of

membership of

 to





rules the fluorescence

quantum yield for an ensemble of molecules. The

values of the degrees of membership of

 to the

two Fuzzy sets can be modulated through external

macroscopic parameters, such as T and HBD ability

of solvent.

150

200

250

300

350

0.0

0.4

0.8

1.2

1.6

0.1

0.2



Figure 3: Dependence of the fluorescence quantum yield

(

) of 6(5H)-Phenathridinone on temperature (T) and

Hydrogen Bonding Donation (HBD) power of the solvent.

It ensues that FLS can be built by means of this

class of compounds with T and HBD ability of the

solvent as inputs,



as output and ultraviolet (UV)

radiation as power supply. Through the Mamdani’s

or Sugeno’s methods, the input and output variables

are fuzzified, i.e. they are partitioned in Fuzzy sets,

defining their related membership functions (μ) and

assigning linguistic variables to each Fuzzy set. IF-

THEN statements, wherein the multiple antecedents

are connected through the AND operator, are fixed

as rules. Each Fuzzy rule is interpreted as a Fuzzy

implication. Since the antecedent parts of the rules

are connected through the AND operator and the

cornerstone of scientific modelling, i.e. the cause

and effect relation, has to be respected, the

membership functions of the rules (

),( kj



) are

defined only by the minimum (equation 3) and the

product (equation 4) t-norms:





)(),(),(min

,),(

FFFR

kjkjkj

HBDT 





(3)





)()()(

,),(

FFFR

kjkjkj

HBDT 







(4)

As the way of determining

),( kj



is fixed, it is

necessary to specify how to combine the IF-THEN

rules. Generally, they are combined through the t-

conorm operator, i.e. the Fuzzy union. The last

element of a FLS is the defuzzifier. A criterion for

its choice can be based on the attempt of optimising

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

208

the prediction capabilities that the built FLS exhibit

towards the Proximity Effect phenomenon of 6(5H)-

phenanthridinone.

Another example of molecular system whereby

Fuzzy logic can be processed is offered by

tryptophan (Gentili, 2008a). When tryptophan

absorbs an UV photon, it passes from the electronic

ground state (S

) to the first excited state (S

). In S

tryptophan is unstable. It decays in a few

nanoseconds by following different paths (see

Figure 4): it can emit light (fluorescence); it can

relax by dissipating the electronic energy in heat

(thermal relaxation); it can chemically transform by

electron or proton transfer reactions and finally, in

the presence of an effective fluorescence quencher,

such as flindersine, it can transfer its energy in

excess (Gentili, 2008b). These different relaxation

pathways are in kinetic competition: the faster the

route, the higher the probability of occurring and

hence its quantum yield. It is possible to influence

the speed of some of these processes and hence the

fluorescence quantum yield (



) through external

physical and chemical inputs, such as the

temperature (T) and the content of the quencher

flindersine. At low temperature and in the absence of

flindersine,



is high. By increasing T, 

weakens

slightly since it becomes easier the thermal activated

reaction path, i.e. the energy barrier, E

act

, is more

easily overcome (see Figure 4).

Figure 4: Relaxation dynamics of tryptophan after photo-

excitation.



is also reduced by adding the quencher

flindersine. Since



varies smoothly with T and the

moles of flindersine, it is possible to exploit the

photobehaviour of tryptophan to implement Fuzzy

Logic Systems (Gentili, 2008a). The temperature

and the extent of flindersine act as inputs, UV

photons as power supply and



of tryptophan as

output. In ways similar to those explained above for

6(5H)-Phenanthridinone, the macroscopic variables

involved are fuzzified; Fuzzy rules, wherein the

multiple antecedents are connected through the

AND operator, are defined and Fuzzy Inference

Engines area started up, based upon the cornerstone

of scientific modelling, i.e. the cause and effect

relation.

There are also chemical reactions that allow

Fuzzy logic to be processed. An example is the

biochemical reaction network controlling the

glycolysis/gluconeogenesis functions (Arkin, 1994).

Here, fructose-6-phosphate (F6P) is interconverted

between its two bisphosphate forms by specific

kinases and phosphatases. The enzymes in this

kinetic mechanism are under the allosteric control of

many of the chemical signals of cellular energy

status such as cyclic-adenosine-monophosphate

(cAMP) and citrate. The dependence of the

concentration of F6P on those of cAMP and citrate,

gives rise to a 3D surface showing a not abrupt

transition from low to high values, such as that of

Figure 3. The profile of the 3D surface has a smooth

hyperbolic shape and not a steep sigmoidal response:

it is suited to process Fuzzy logic.

Another example of a Fuzzy chemical reaction is

DNA hybridisation wherein two single-stranded

DNA molecules (oligonucleotides) bind to form a

double stranded DNA duplex. At room temperature,

the hybridisation reaction is not a two-state, all or

none process, but it is inherently Fuzzy because it is

a continuum of outcomes (Deaton, 2001). The pairs

of oligonucleotides formed inside a test tube cannot

be divided into distinct sets of hybridised and

unhybridised species, but each molecule would have

a degree of membership in both.

The best implementations of Fuzzy Logic

Systems are human senses, that have to be mimicked

by Information Technology in order to reach high

intelligent quotients in artificial intelligence. Sight,

hearing, taste, smell and touch are inherently fuzzy.

They fuzzify the crisp inputs coming from the

outside and send the information to the human brain,

that is a Fuzzy inference engine, capable of facing

up problems based on subjective or imprecise

knowledge. Senses are based on a discrete number

of perceiving cells acting as Fuzzy sets (Gentili,

2009). For example, in the case of colour perception,

we have three types of cones, whereby we

distinguish colours: one cone absorbing mainly the

blue portion of the visible spectrum, another

absorbing mainly the green and the third principally

sensitive to the red. Their absorption spectra in the

MOLECULAR FUZZY INFERENCE ENGINES - Development of Chemical Systems to Process Fuzzy Logic at the

Molecular Level

209

visible, can be conceived as Fuzzy sets, having

Gaussian shape: one centred at 437 nm, the other

centred at 533 nm and the third centred at 564 nm.

When a radiation, having wavelengths included in

the visible, hits the retina of our eyes, it activates the

three cones in a specific proportion, i.e. it will have

specific values of membership functions in three

Fuzzy sets. Each combination for the values of three

membership functions will be transduced into the

perception of a specific colour inside our brain.

4 CONCLUSIONS

Computers of the future will probably consist of

molecular processors. Atoms and molecules process

quantum logic. However, the insidious actions of the

environment trigger detrimental decoherent effects

on the qubits. If decoherent phenomena acting on the

qubits are unavoidable, it is still possible to compute

with molecules by abandoning the lure of quantum

logic and processing classical logic. When

computations are carried out by single molecules,

only Boolean logic gates can be implemented. When

computations are performed through a huge

collection of molecules, both Boolean and Fuzzy

logic can be processed. If the input-output relations

are abrupt and they have sigmoidal shape, they are

suited to implement binary logic gates. If, on the

other hand, the output varies smoothly with the

inputs, their relation become suited to implement

Fuzzy inference engines. Photo-responses of

molecules such as 6(5H)-Phenanthridinone and

tryptophan can be used to realize Fuzzy Logic

Systems wherein the multiple antecedents are

connected through the AND operator. New chemical

systems have to be found to process complete Fuzzy

Inference engines. They will be implemented by

following either the strategy of the “interfacial

hardware” or that of “wetware”. The possibility of

processing Fuzzy logic at the molecular level will

allow high quotients to be within reach of the

Artificial Intelligence.

ACKNOWLEDGEMENTS

This research was funded by the Ministero per

l’Università e la Ricerca Scientifica e Tecnologica

(Rome, Italy) and the University of Perugia

(PRIN2008, 20088NTBKR).

REFERENCES

Adlemann, L. M., 1994. Molecular Computation of

solutions to combinatorial problems. In Science. 266,

1021-1024.

Arkin, A., Ross, J., 1994. Computational Functions in

Biochemical Reaction Networks. In Biophys. J. 67,

560-578.

Bennet, C. H., DiVincenzo, D. P., 2000. Quantum

information and computation. In Nature. 404, 247-

255.

Deaton, R., Garzon, M., 2001. Fuzzy logic with

biomolecules. In Soft Computing. 5, 2-9.

Feynman, R. P., 1960. There’s plenty of room at the

bottom. In Eng. Sci. 23, 22-36.

Gentili, P. L., Ortica, F., Romani, A., Favaro, G., 2007a.

Effects of proximity on the relaxation dynamics of

Flindersine and 6(5H)-Phenanthridinone. In J. Phys.

Chem. A. 111, 193-200.

Gentili, P. L., 2007b. Boolean and Fuzzy logic

implemented at the molecular level. In Chem. Phys.

336, 64-73.

Gentili, P. L., 2008a. Boolean and Fuzzy Logic Gates

Based on the Interaction of Flindersine with Bovine

Serum Albumin and Tryptophan. In J. Phys. Chem. A.

112, 11992-11997.

Gentili, P. L., Ortica, F., Favaro, G., 2008b. Static and

Dynamic Interaction of a Naturally Occurring

Photochromic Molecule with Bovine Serum Albumin

studied by UV-Visible Absorption and Fluorescence

Spectroscopy. In J. Phys. Chem. B. 112, 16793-16801.

Gentili, P. L., 2009. Fuzzy Logic in Molecular Computing.

In Fuzzy Logic: Theory, Programming and

Applications, Editor R. E. Vargas, Nova Science

Publishers, Hauppauge, NY.

Jurvetson, S. T., 2004. Transcending Moore's Law with

Molecular Electronics and Nanotechnology. In

Nanotech. L. and Business. 1, 70-90.

Lim, E. C., 1986. Proximity Effect in Molecular

Photophysics: Dynamical Consequences of Pseudo-

Jahn-Teller Interaction. In J. Phys. Chem.90, 6770-

6777.

Plenio, M. B., Virmani, S., 2007. An introduction to

entanglement measures. Quant. Inf. Comp. 7, 1-51.

Schumacher, B., 1995. Quantum Coding. Phys. Rev. A. 51,

2738-2747.

Siebrand, W., Zgierski, M. Z., 1980. Radiationless decay

of vibronically coupled electronic states. In J. Chem.

Phys. 72, 1641-1646.

Szaciłowski, K., 2008. Digital Information Processing in

Molecular Systems. In Chem. Rev. 108, 3481-3548.

Zadeh, L. A., 1994. Soft Computing and Fuzzy Logic. In

IEEE Software. 11, 48-56.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

210