
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME
LEARNING MACHINES
Monther Alhamdoosh, Castrense Savojardo, Piero Fariselli and Rita Casadio
Biocomputing Group, University of Bologna, Via Irnerio 42, 40127 Bologna, Italy
Keywords:
Disulfide connectivity, Disulfide bonds, Extreme learning machine, Backpropagation, ELM outperforms BP,
Multiple feature vectors, Disulfide proteins, Disulfide bridge prediction, K-mean clustering with ELM, RBF
networks with ELM, SLFN with ELM.
Abstract:
Our paper emphasizes the relevance of Extreme Learning Machine (ELM) in Bioinformatics applications by
addressing the problem of predicting the disulfide connectivity from protein sequences. We test different
activation functions of the hidden neurons and we show that for the task at hand the Radial Basis Functions
are the best performing. We also show that the ELM approach performs better than the Back Propagation
learning algorithm both in terms of generalization accuracy and running time. Moreover, we find that for the
problem of the prediction of the disulfide connectivity it is possible to increase the predicting performance by
initializing the Radial Basis Function kernels with a k-mean clustering algorithm.
Finally, the ELM procedure is not only very fast but the final predicting networks can achieve an accuracy of
0.51 and 0.45, per-bonds and per-pattern, respectively. Our ELM results are in line with the state of the art
predictors addressing the same problem.
1 INTRODUCTION
The prediction of protein structures from their se-
quences is still an open problem in Structural Bioin-
formatics, especially considering that the dispropor-
tion between the huge number of putative protein se-
quences with respect to the smaller number of known
3D structures. Over the last two decades several ap-
proaches were described in order to find approximate
solutions to the protein folding problem and tools
have been developed to facilitate the search of a likely
structural template for the protein sequence at hand.
Among these, the identification of the correct pairing
of bonded cysteines in the protein sequence (disulfide
connectivity) helps in constraining its folded struc-
ture.
The problem of the prediction of disulfide connec-
tivity can be logically split into two steps: 1) predict-
ing the disulfide-bonding state (namely the identifica-
tion of the cysteine residues that in the protein chain
are/are not likely to make disulfide bonds); 2) assign-
ing the connectivity pattern of the bonded cysteines.
For the first step several methods are available and
achieve an average per-protein accuracy higher than
80% (Muskal et al., 1990; Fiser et al., 1992; Fariselli
et al., 1999; Fiser and Simon, 2000; Mucchielli-
Giorgi et al., 2002; Martelli et al., 2002; Chen et al.,
2004; Liu, 2007). Finding solutions for the second
step is generally harder than for the first one, since
cysteine pairing in the protein space is a problem
of global optimization in the protein feature space
and the bridge formation is not necessarily depen-
dent on local functional and structural motifs. Ma-
chine learning and computational methods have been
widely used to solve the disulfide connectivity pre-
diction problem over the past years with significant
progresses.
Fariselli and Casadio (2001) first addressed the
prediction of disulfide connectivity as a combinatorial
optimization problem that finds the maximum-weight
perfect matching of a complete undirected weighted
graph. According to this graph model vertices are
the putative bonded cysteines and edges represent
the strength of interactions among corresponding cys-
teine pairs. Since the graph is complete, the Edmond-
Gabows (EG) algorithm (Gabow, 1975) is the most
suitable method to solve the corresponding Linear
Programming problem. The weight edges were com-
puted using stochastic optimization methods (Fariselli
and Casadio, 2001) or neural networks (Fariselli et al.,
2002; Shi et al., 2008).
Later other methods were developed and these in-
5
Alhamdoosh M., Savojardo C., Fariselli P. and Casadio R..
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME LEARNING MACHINES.
DOI: 10.5220/0003125600050014
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 5-14
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

clude a bi-recursiveneural network system (Vullo and
Frasconi, 2004), a method based on Cysteine Separa-
tion Profiles (CSPs) (Zhao et al., 2005), neural net-
works that exploit diresidue composition (Ferr`e and
Clote, 2005), two dimensional recursive neural net-
works (Baldi et al., 2005), K-nearest neighbors algo-
rithm (Chen et al., 2006), support vector regression
(Song et al., 2007; Zhu et al., 2010), support vec-
tor machines (Lu et al., 2007), statistical analysis in-
cluding correlated mutations (Rubinstein and Fiser,
2008), decomposition convolution kernels (Vincent
et al., 2008) and recently prediction based on com-
parative modeling (Lin and Tseng, 2010).
Although it is difficult to compare the perfor-
mance of different predictors, often trained and tested
on different protein sets with different levels of ho-
mology, and implementing different protein features,
the present best performance is in the range of 50-
60% per protein accuracy depending on the num-
ber of disulfide bridges. In any case all the above
approaches are poorly performing when the num-
ber of bridges in the protein is ≥5. This was/and
still remains due to the paucity of examples in the
PDB database of proteins with a large number (≥5)
of disulfide bridges included in the training/testing
set. In most of the neural network based methods
quoted above the networks were modeled as directed
acyclic graphs (DAG) trained with the very popu-
lar back-propagation (BP) algorithm that implements
the steepest gradient descent (GD) search through the
space of network weights. Trapping in local minima
is one of the major problem of this procedure and
the search in the weights space is generally slow and
time-consuming, especially considering that the num-
ber of training examples in the biological data bases
is exponentially increasing and methods need learn-
ing updating.
In this paper, we are approaching the problem of
disulfide connectivity prediction using single-hidden
layer feed-forwardneural network (SLFN), with a lat-
est machine learning technology called the Extreme
Learning Machine (ELM) (Huang et al., 2004). We
investigate the performanceof this algorithm with dif-
ferent activation functions as compared to the classi-
cal BP approach. We find that the ELM procedure
is very fast and that the final predicting networks can
achieve an accuracy of 0.51 and 0.45, per-bonds and
per-pattern respectively. Our ELM results are there-
fore in line with the state of the art predictors address-
ing the same problem and are obtained with less com-
putational time.
The remainder of the paper is organized as fol-
lows: Section 2 describes the ELM learning algo-
rithm. Section 3 presents our dataset and the exper-
imental protocol of our work. Section 4 shows and
discusses results, and concludes this paper.
2 BRIEF OF THE EXTREME
LEARNING MACHINE
Single-hidden layer feed-forward neural network
(SLFN) have been showed to be sufficient to solve
very difficult mapping (Huang, 2003; Tamura and
Tateishi, 1997). However, traditional learning al-
gorithms for feed-forward networks, like back-
propagation, require tuning many parameters over an
iterative procedure that is very time-consuming. To
overcome this issue, in the recent years the Extreme
Learning Machines have been introduced (Huang
et al., 2006b; Huang et al., 2004; Huang and Siew,
2004; Huang and Siew, 2005; Huang et al., 2006a).
For sake of clarity we briefly introduce the mathemat-
ical notation used to define ELM.
2.1 Mathematical Perspective on SLFNs
For N arbitrary distinct samples (x
i
,t
i
), where x
i
=
[x
i1
,x
i2
,··· ,x
in
]
T
∈ R
n
and t
i
= [t
i1
,t
i2
,··· ,t
im
]
T
∈ R
m
, a standard SLFN with N hidden neurons and an ac-
tivation function g(x) is mathematically modeled as
˜
N
∑
i=1
β
i
g(w
i
.x
j
+ b
i
) = o
j
, j = 1, · · · ,N (1)
where w
i
= [w
i1
,w
i2
,··· ,w
in
]
T
is the weight vector
connecting the ith hidden neuron and the input neu-
rons, β
i
= [β
i1
,β
i2
,··· ,β
im
]
T
is the weight vector con-
necting the ith hidden neuron and the output neurons,
and b
i
is the threshold of the ith hidden neuron. w
i
·x
j
denotes the inner product of w
i
and x
j
. The standard
SLFNs can approximate these N samples with zero
error if there exist β
i
, w
i
and b
i
such that
˜
N
∑
i=1
β
i
g(w
i
.x
j
+ b
i
) = t
j
, j = 1,··· ,N (2)
The above N equations can be written compactly as:
Hβ = T (3)
where
H(w
1
,··· ,w
N
,b
1
,··· ,b
N
,x
1
,··· ,x
N
) =
g(w
1
.x
1
+ b
1
) ··· g(w
˜
N
.x
1
+ b
˜
N
)
.
.
. ···
.
.
.
g(w
1
.x
N
+ b
1
) ··· g(w
˜
N
.x
N
+ b
˜
N
)
N×
˜
N
(4)
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
6

β =
β
T
1
.
.
.
β
N
˜
N
˜
N×m
and T =
t
T
1
.
.
.
t
N
˜
N
˜
N×m
(5)
H is called the hidden layer output matrix of the neu-
ral network (Huang, 2003); the ith column of H is
the ith hidden neuron output with respect to inputs
x
1
,x
2
,...,x
N
.
The same formulation can be extended to Radial
Basis Function (RBF) networks, where each g(w
i
.x
i
+
b
i
) in the hidden layer matrix H is substituted with a
RBF kernel:
φ
i
(x) = φ
kx− µ
i
k
σ
i
(6)
where µ
i
= [µ
i1
,µ
i2
,...,µ
in
]
T
is the ith kernel´s center
and σ
i
is its impact width.
2.2 ELM Learning Algorithm
Since the number of distinct training examples is usu-
ally much greater than the number of hidden neu-
rons (N ≫
˜
N), the H matrix is a rectangular matrix
and tuning the parameters w
i
,b
i
,β
i
or µ
i
,σ
i
,β
i
(i =
1,...,
˜
N) in order to obtain a unique solution for Hβ =
T is not always possible. Gradient–based learning al-
gorithms try to find a solution that minimizes the cost
function
E =
N
∑
j=1
˜
N
∑
i=1
β
i
f
i
(x
j
) −t
j
!
2
(7)
where f
i
(x
j
) is the output of the ith hidden neuron
(additive or RBF kernel) when the training sample x
j
is introduced to the network.
Seeking simplicity, Huang et al. (Huang et al.,
2004; Huang and Siew, 2004; Huang and Siew, 2005;
Huang et al., 2006a) showed that there is no need to
tune the input weights and biases of hidden neurons
or of the kernel parameters and that they can be ran-
domly set and then fixed. Assuming the input weights
and biases or kernel parameters are fixed, the training
of SLFN is simply finding a solution
ˆ
β for the linear
system Hβ = T. Usually this is achieved by adopting
the Moor-Penrose generalized inverse (see theorem in
P.147 of (Serre, 2002)), as:
ˆ
β = H
†
T (8)
where H
†
is the pseudoinverse matrix of the hidden
layer output matrix H. As analyzed by Huang et
al., this method can reach good generalization per-
formance by ensuring two properties of learning: the
smallest norm of weights besides the smallest squared
error on the training samples, while the gradient-
based algorithms focuses on the later property only.
The three main steps involved in ELM algorithm can
be summarized as:
ELM Algorithm (Huang et al., 2004; Huang and
Siew, 2004). Given a training set D = {(x
i
,t
i
)|x
i
∈
R
n
,t
i
∈ R
m
,i = 1, . . . ,N}, activation function g or ker-
nel function φ, and number of hidden neurons or ker-
nels
˜
N,
Step 1 Assign randomly input weights w
i
and biases
b
i
for additiveneurons or centers µ
i
and impact widths
σ
i
,i = 1, . . . ,
˜
N for RBF kernels.
Step 2 Calculate the hidden layer output matrix H.
Step 3 Calculate the output weights β:
ˆ
β = H
†
T.
The efficiency of this algorithm comes from its
ability to use many nonlinear activation and kernel
functions without restriction for being differential,
and to avoid the troubling issues such as stopping cri-
teria, learning rate, learning epochs and local minima.
3 IMPLEMENTATION AND
METHODS
3.1 Dataset PDB0909
From the Protein Data Bank (PDB) (Berman et al.,
2000), release of September 2009 we retrieved all
protein structures that are resolved by X-ray experi-
ments with resolution between 0 and 2.5 A
◦
. Simi-
lar sequences were removed at 70% identity, then the
chain with longest length and highest resolution for
each protein was selected. To eliminate the redun-
dancy we followed this procedure: an all-against-all
BLAST (Altschul et al., 1990) sequence search was
performed on the starting protein set, then we clus-
tered similar chains together (as connected compo-
nents of an undirected graph) and only the longest
chain of each cluster was retained as representative.
Two protein chains are defined similar if they share a
sequence identity > 25% and an alignment coverage
> 80%. After this basic filtering process, we sorted
out only the protein chains that have at least two intra-
chain bonded cysteines, so that we ended up with 796
chains. In our study, we only focus on the chains that
have 2, 3, 4, and 5 intra-chain disulfide bonds since
chains with more than 5 bridges are very few and can-
not be statistically tested (chains with one disulfide
bridge are trivial cases). Table 1 shows the number
of chains with 2, 3, 4 and 5 bridges and other statis-
tics about each connectivity size. The % Coverage of
Patterns Space column shows the lack of patterns rep-
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME LEARNING MACHINES
7

resentation when the number of bonded cysteines gets
higher than eight.
3.2 Cross-validation Sets
A 4-fold cross-validation procedure was used to eval-
uate the performance of our predictor, in which the
dataset is partitioned into four almost-equal-size sub-
sets. The results obtained for the four tests are com-
bined to produce a single evaluation. In order to
guarantee the absence of homology among the folds
we further re-aligned with BLAST all the sequences
against themselves. We then defined two sequences as
similar if their identity is > 25%. According to this
labeling, similar sequences were then clustered and
chains of the same cluster were assigned to the same
cross-validation fold.
3.3 Measures of Performance
Given a protein primary sequence with N(= 2B) cys-
teines forming B disulfide bridges, the number of pos-
sible cysteine pairs is:
N
c
=
2B
2
=
2B!
2!(2B− 2)!
= B(2B− 1), (9)
and the number of possible connectivity patterns is:
N
p
= (2B− 1)!! =
(2n)!
2
n
.n!
(10)
The number of possible connectivity patterns dra-
matically grows as the number of disulfide bridges in-
creases. For this reason among the several indexes
that can be used to score the predictions (Ferr`e and
Clote, 2005; Baldi et al., 2005), the most informative
are: the disulfide bond index Q
c
and disulfide pattern
index Q
p
(Fariselli and Casadio, 2001). Q
p
, globally
evaluates the ability of a predictivesystem to correctly
predict disulfide connectivity patterns and is given by:
Q
p
=
∑
T
p
i=1
δ
i
(x,y)
T
p
, (11)
where δ
i
(x,y) is equal to 1 if the predicted pattern y of
the ith protein coincides with its correct pattern x and
T
p
is the total number of predicted protein chains. In
4-fold cross-validation, we collect the numbers of cor-
rectly predicted patterns from all folds, and then av-
erage them over the size of the un-partitioned dataset.
Alternatively, Q
c
is a pair-wise index that estimates
the predictive accuracy of individual disulfide bonds
i.e. the percentage of disulfide bridges that are cor-
rectly predicted, and is given by:
Q
c
=
∑
T
p
i=1
∑
B
j=1
δ
j
(x,y)
T
c
, (12)
where δ
j
(x,y) is equal to 1 if the jth predicted disul-
fide bond y of the ith predicted pattern coincides with
a correct disulfide bond x in the correct pattern, B
is the connectivity size of the ith pattern, and T
c
is
the total number of possible pairs in the T
p
proteins.
Similarly, the numbers of correctly predicted pairs are
collected from all folds during cross-validation and
the total Q
c
value is computed by averaging these
numbers over the total number of pairs in the un-
partitioned dataset.
To score the performance we define a random pre-
dictor R
p
without bias a predictor that assigns ran-
domly the bonding pairs. For R
p
the performances
can be theoretically computed as:
Q
p
(R
p
) =
1
N
p
=
1
(2B− 1)!!
(13)
Q
c
(R
p
) =
B
N
c
=
B
B(2B− 1)
=
1
2B− 1
(14)
Q
p
(R
p
) is vanishing much faster than Q
c
(R
p
)
although both depend on the number of disulfide
bridges.
3.4 Multiple Feature Vectors
To assign pairwise probabilities we defined vectors
that represent each cysteine pairs and some global
protein descriptors (Song et al., 2007).
Local Descriptors
Evolutionary information: this descriptor consti-
tutes the largest portion of our multiple sequence fea-
ture vectors that it is composed of w∗ 20 ∗ 2 compo-
nents when the neighbor amino acidic residues around
the two cysteine forming disufide bond are comprised
in a window of size w. We evaluate different window
sizes of the cysteine local context and found out that
w= 13 (six residues flanking the cysteine at each side)
is the most appropriate value. Each position in the
neighbor environment of cysteines, including the cys-
teine position, is encoded with 20 values that are the
frequencies of each residue at this particular position.
This evolutionary information is obtained using the
PSI-BLAST program (Altschul et al., 1997) from the
multiple sequence alignment portrayed in the form of
position-specific scoring matrices (PSSM). The PSI-
BLAST was run against the non-redundant database
for 3 iterations with an E-value cutoff of 0.001.
Secondary Structure Information: it is also a key
player in improving the prediction accuracy increas-
ing the training vectors with new informative at-
tributes relative to the local environment of cysteines.
In this paper, the DSSP program (Kabsch and Sander,
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
8

Table 1: The PDB0909 Dataset. % Coverage of Patterns Space represents the percentage of disulfide patterns, out of all
possible patterns, that are observed in our dataset. e.g. for B=2, the patterns space contains 3 patterns (C1C2, C3C4), (C1C3,
C2C4), (C1C4, C2C3). % Coverage of Pairs Space represents the same value, but in terms of ordered cysteine pairs. e.g. for
B=2, the pairs space is composed of 6 pairs (C1C2, C1C3, C1C4, C2C3, C2C4, C3C4).
Connectivity
Size (B)
# of
Chains
# of Bonded
Cysteines
# of Free
Cysteines
Total # of
Cysteines
% Coverage of
Patterns Space
% Coverage of
Pairs Space
2 146 584 103 687 100 100
3 104 624 60 684 100 100
4 52 416 20 436 25.71 100
5 40 400 17 417 3.39 84.44
Total 342 2024 200 2224 7.21 92.55
1983) was used to obtain the secondary structure in-
formation which was encoded into a 3-letters repre-
sentation. The letter A represents the alpha helix (H),
3-helix (G) and 5 helix (I) from the DSSP output, the
letter B encodes for the residues in isolated bridges
(B) and extended strands (E) in the DSSP output, and
finally the letter C stands for the hydrogen bonded
turns (T), the bends (S) and the loops and irregular el-
ements (blank). Technically, each letter was encoded
by three binary bits: 100 for A, 010 for B, 001 for
C and 000 for X (empty place). This descriptor con-
tributes 39 components (13∗3) for each training vec-
tor when w = 13.
Global Descriptors
Residues Composition: it describes the residues
content in a protein sequence as 20-dimensions vec-
tor of the relative frequencies of residues of different
types. These dimensions can be mathematically for-
mulated as following:
AA
i
=
n
i
L
;i = 1, . . . , 20 (15)
where n
i
is the number of occurrences of the residues
of type i in the sequence and L is the length of the
protein sequence.
Protein Sequence Length: when considering a
protein i with
´
L
i
residues from a proteins dataset, the
normalized protein length L
i
is given by:
L
i
=
´
L
i
−
¯
L
SD
(16)
where the mean protein length
¯
L and the standard de-
viation SD of protein lengths are computed on the
whole dataset.
Protein Molecular Weight: similarly to the equa-
tion above, for a protein i with M
i
total molecular
weight we normalized the value as:
M
i
=
´
M
i
−
¯
M
SD
(17)
where the mean molecular weight
¯
M and the standard
deviation SD are computed on the whole dataset. The
Figure 1: The testing accuracy of prediction when using ad-
ditive neurons and training different connectivity sizes to-
gether. The red, blue, green and magenta curves represent
the accuracies for 2, 3, 4 and 5 connectivty sizes, repsec-
tively. The black curve represents the overall accuracy re-
gardless of the connectivity size.
molecular weight values for the single residues are
taken from ProtScale (Gasteiger et al., 2005).
Cysteines Separation Distance: we coded the cys-
teine sequence separation as:
SEP(C
i
,C
j
) = log(| j − i|) (18)
where i and j are the sequence positions of cysteines
C
i
and C
j
, respectively.
Relative Order of Cysteines: this feature en-
codes for two different values of the input vec-
tor, representing the normalized relative order of
the two cysteines. For instance, given a pro-
tein P with 4 cysteines (C
1
,C
2
,C
3
,C
4
) the cor-
responding normalized ordered list of cysteine is
(1/4,2/4,3/4, 4/4) = (0.25,0.5,0.75,1). So that
when the method train/predict a pair of cysteines the
two corresponding values are taken from the list (e.g.
the pair [C
2
,C
3
] is encoded as [0.5,0.75]).
As a result, the final training/testing vectors consist
of 623 components based on these protein sequence
features.
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME LEARNING MACHINES
9

Figure 2: The testing accuracy of prediction when using
L1 RBF kernels and training different connectivity sizes to-
gether.
Figure 3: The general scheme of our proposed disulfide
connectivity prediction method. The steps of our procedure
have been illustrated for the chain F of Interleukin-15 re-
ceptor protein whose PDB ID 2PSM.
3.5 Experimental Protocol
The implementation of the proposed model (see Fig-
ure 3) was done using the free scripting language
Python 2.6 (Van Rossum et al., 1991) along with its
numerical package Numpy 1.3 (Oliphant, 2006), used
to compute the pseudo-inverse matrix of the matrix
H in the ELM learning algorithm. Single experi-
ment with different numbers of additive and kernel
hidden neurons have been carried out to find the best
estimation of the hidden layers size. Since some of
the network parameters are randomly initialized, each
experiment was run 50 times and then the average
measurementswere taken to evaluate the performance
of our Model. The additive neurons were activated
using the sigmoid activation function g(x) =
1
1+e
−x
while two Gaussian functions L
1
(x) = e
−kx−µk
σ
and
L
2
(x) = e
−kx−µk
2
σ
2
were tested for the RBF kernels. Fur-
thermore, one output neuron was used in most of the
experiments unless otherwise mentioned. We also ex-
amined the performance of the Backpropagation (BP)
learning algorithm on SLFNs with a symmetric sig-
moid activation function for the hidden layer and a
sigmoid activation function for the output layer. The
learning rate was set to 0.1 and MSE threshold error to
0.0001. Interestingly, early stopping condition based
on the accuracy of validation sets has been also em-
ployed to avoid overfitting of training data and reduce
training time. The online incremental approach was
used to update weights.
The simulations were executed on a computer of
8 processors, each one with 2.5 GHz frequency, and
16 GB of RAM.
4 RESULTS AND DISCUSSION
We first evaluate the SLFN performance as a function
of the number of hidden units adopting a four-fold
cross validation procedure. The results at increasing
number of additive neurons are reported in Figure 1
for the disulfide pattern index Qp. Similar graphs re-
porting the Qp values are shown in Figures 2 and 4
when the transfer function during the learning phase
is the Gaussian function with L1 and L2 norms. In
all reported cases, the SLFN performance reaches a
plateau when the number of hidden neuron is larger
than 100. It is worth noticing that the training time
is nearly a linear function of the number of hidden
neuronsirrespectively of the transfer function adopted
(Figure 5). The accuracy index Qp when plotted as a
function of the number of hidden units obtained with
the Back Propagation (BP) learning algorithm is less
stable then that obtained with the EML learning (com-
pare Fig.1,2,4 with Figure 6). Furthermore, the BP
training time as a function of the number of hidden
neurons shows a significantly steeper slope with re-
spect to the ELM approach (compare Figures 5(a) and
5(b) with Figure 7). These results highlight the ef-
fective time saving of ELM with respect to BP when
training is performed. The detailed results for the best
performing number of neurons for the different SLFN
models are reported in Table 2, where it is listed that
the RBF networks with L1 function achieve the best
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
10
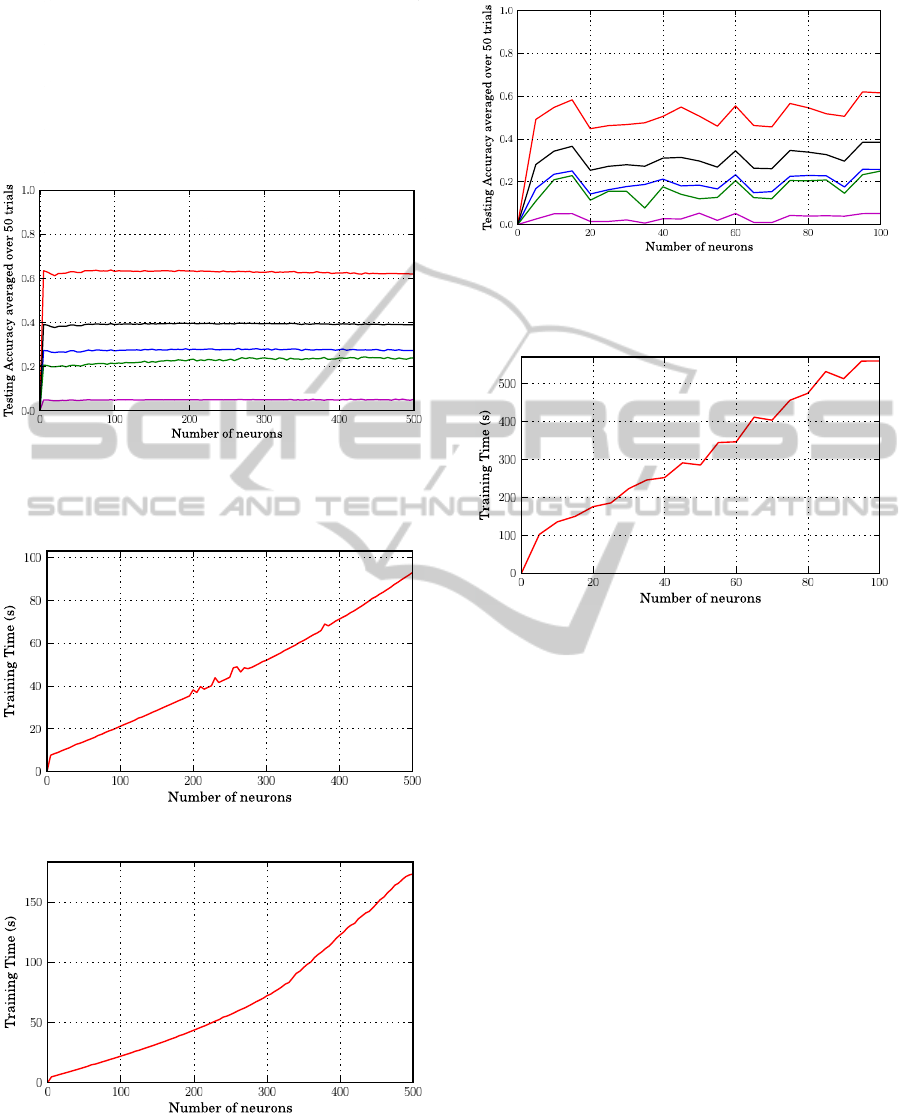
overall performance both in term of Qc and Qp . This
picture holds also when the performance is evaluated
separately for each subset comprising proteins with a
different number of disulfide bonds (Table 2). Table
2 reports also the required learning time, and it ap-
pears that the Back Propagation (BP) algorithm is far
slower than the ELM algorithm.
Figure 4: The testing accuracy of prediction when using
L2 RBF kernels and training different connectivity sizes to-
gether.
(a) Additive hidden neurons.
(b) RBF hidden neurons.
Figure 5: The training time of SLFNs over 4-folds cross-
validation procedure when training different connectivity
sizes together.
Figure 6: The testing accuracy of prediction when using BP
learning algorithm and training different connectivity sizes
together.
Figure 7: The training time of SLFNs over 4-folds cross-
validation procedure when using BP learning algorithm and
training different connectivity sizes together.
4.1 Performance Enhancement
Instead of random initializing the first layers of
weights, we select them using a standard K-mean
clustering approach to set the centers and impact
widths of kernels. The value of the selected number of
clusters K corresponds to the number of hidden neu-
rons. Next, for each hidden kernel its center is set by
the center of a cluster while its impact width is set
as the standard deviation of the cluster vectors from
its center. The performance of ELM with L1 Gaus-
sian functions and K-mean clustering algorithm is re-
ported in Figure 8 for Qp. The training time is dom-
inated by the K-mean clustering procedure and can
be several times greater than the random initialization
(compare Figure 9 with Figure 5). This is particu-
lar evident by considering that the K-mean clustering
running time increases with the number of clusters
(K) up to a given threshold that depends on the ratio
between the number of data and the K value.
Then the training time as a function of the num-
ber of hidden neurons decreases (Figure 9), becom-
ing constant when K equates the number of elements
to cluster. Nonetheless, the best results obtained by
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME LEARNING MACHINES
11

Table 2: Comparison of different ELM-trained models with BP-trained model when different connectivity sizes are trained
together. N
H
is the best number of hidden neurons (when additive) and kernels (when RBF). Qc and Qp (%) have been
thoroughly explained earlier. ELM (Sig) is a neural network trained with ELM algorithm using sigmoid activation function
for the hidden neurons. ELM (L
i
RBF) is an RBF neural network trained with ELM algorithm using L
i
Gaussian function.
Time (s) is the average training time, given in seconds, of 50 experiments.
Model
B = 2 B = 3 B = 4 B = 5 Overall Best # of
neurons
Time
(s)Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
ELM (Sig) 65 65 42 28 42 24 27 4 46 41 150 28.52
ELM (L
1
RBF) 66 66 45 32 45 26 31 5 48 43 90 18.55
ELM (L
2
RBF) 64 64 42 28 39 22 28 5 45 40 95 18.55
BP 62 62 38 26 40 23 29 5 44 38 95 559.29
Figure 8: The testing accuracy of prediction when using K-
Mean clustering algorithm to initialize L1 RBF kernels and
training different connectivity sizes togehther.
Figure 9: The training time of SLFNs over 4-folds cross-
validation procedure when using K-mean clustering algo-
rithm to initialize RBF kernels and training different con-
nectivity sizes together.
using the K-mean clustering initialization are slightly
better than the random initialization approach (Table
3).
4.2 Comparison with some Previous
Works
As mentioned in the introduction it is not easy to com-
pare our results with those obtained before, since dif-
Table 3: Our method performance with L1 RBF kernels ini-
tialized using k-mean clustering. The best number of hid-
den neurons is 270 and the corresponding training time is
425.11 seconds.
Connectivity Size 2 3 4 5 overall
Q
c
67 48 44 37 51
Q
p
67 36 27 6 45
ferent authors adopted different datasets (sometimes
without reducing the sequence identity between train-
ing and testing sets). Nonetheless for sake of clarity
in Table 4 we compare our best ELM cross-validation
performance with the Random predictor R
p
, the his-
torical benchmark Fariselli et al. 2002, and two state
of the art methods Vullo and Frasconi (2004) and
Baldi et al. (2005). It is evident that all the meth-
ods perform better than the random predictor and that
the ELM approach compare very well with the state
of the art methods making it a fast and efficient al-
ternative when the problem of the prediction of the
disulfide connectivity is addressed.
5 CONCLUSIONS
In this paper we address the problem of the prediction
of the disulfide connectivity using an Extreme Learn-
ing Machine approach. We test different activation
functions of the hidden neurons and different way of
initializing the first layer of weights. We also evalu-
ate the performance of the different methods both in
term of accuracy and running times. We show that
the ELM learning is faster and generalizes better than
the corresponding Back Propagation training. Among
our tested models we verify that the RBF neural net-
works trained with an ELM procedure are the best
performing approach for the task at hands. We find
that a K-mean clustering procedure to select the first
layer of weights, improves the overall EML accuracy
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
12

Table 4: Comparison with previous works on disulfide connectivity prediction. These results were generated on a benchmark
dataset called SP39 (Fariselli and Casadio, 2001).
Proposed Method
B = 2 B = 3 B = 4 B = 5 Overall
Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
Q
c
Q
p
R
p
33 33 20 7 14 1 11 0 19 10
Fariselli et al. (2002) 68 68 37 22 37 20 26 2 42 34
Vullo and Frasconi. (2004) 73 73 51 41 37 24 30 13 49 44
Baldi et al. (2005) 74 74 61 51 44 27 41 11 56 49
ELM 72 72 45 33 49 31 44 22 52 45
and that the trained neural system well compares with
the state of the art methods.
ACKNOWLEDGEMENTS
The authors would like to acknowledge Dr. Dianhui
Wang, from the Department of Computer Science and
Computer Engineering at La Trobe University in Aus-
tralia, for his valuable suggestions to utilize ELMs for
the problem at hand.
REFERENCES
Altschul, S. F., Gish, W., Miller, W., Myers, E. W., and
Lipman, D. J. (1990). Basic local alignment search
tool. Journal of Molecular Biology, pages 403–410.
Altschul, S. F., Madden, T. L., Schaffer, A. A., Zhang,
J., Zhang, Z., Miller, W., and Lipman, D. J. (1997).
Gapped blast and psi-blast: a new generation of pro-
tein database search programs. Nucleic Acids Re-
search, 25(17):3389–3402.
Baldi, P., Cheng, J., and Vullo, A. (2005). Large-scale pre-
diction of disulphide bond connectivity. In Saul, L.,
Weiss, Y., and Bottou, L., editors, Advances in Neural
Information Processing Systems, 17, pages 97–104.
MA MIT Press.
Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat,
T. N., Weissig, H., Shindyalov, L. N., and Bourne,
P. E. (2000). The protein data bank. Nucleic Acids
Research, 28(1).
Chen, G., Deng, H., Gui, Y., Pan, Y., and Wang, X. (2006).
Cysteine separations profiles on protein secondary
structure infer disulfide connectivity. In IEEE Inter-
national Conference on Granular Computing.
Chen, Y., Lin, Y.-S., Lin, C.-J., and Hwang, J.-K. (2004).
Prediction of the bonding states of cysteines using
the support vector machines based on multiple fea-
ture vectors and cysteine state sequences. Proteins,
55:1036–1042.
Fariselli, P. and Casadio, R. (2001). Prediction of disulfide
connectivity in proteins. Bioinformatics, 17(10):957–
964.
Fariselli, P., Martelli, P. L., and Casadio, R. (2002). A
neural network-based method for predicting the disul-
fide connectivity in proteins. In Damiani, E., edi-
tor, Knowledge Based Intelligent Information Engi-
neering Systems and Allied Technologies (KES), pages
464–468. Amsterdam IOS Press.
Fariselli, P., Riccobelli, P., and Casadio, R. (1999). Role of
evolutionary information in predicting the disulfide-
bonding state of cysteine in proteins. Proteins,
36:340–346.
Ferr`e, F. and Clote, P. (2005). Disulfide connectivity
prediction using secondary structure information and
diresidue frequencies. Bioinformatics, 21(10):2336–
2346.
Fiser, A., Cserzo, M., Tudos, E., and Simon, I. (1992). Dif-
ferent sequence environments of cysteines and half
cystines in proteins: Application to predict disulfide
forming residues. FEBS, 302(2):117–120.
Fiser, A. and Simon, I. (2000). Predicting the oxidation state
of cysteines by multiple sequence alignment. Bioin-
formatics, 16(3):251–256.
Gabow, H. N. (1975). An efficient implementation of ed-
monds al- gorithm for maximum weight matching on
graphs. Technical Report CU-CS-075-75, Department
of Computer Science, Colorado University.
Gasteiger, E., Hoogland, C., Gattiker, A., Duvaud, S.,
Wilkins, M. R., Appel, R. D., and Bairoch, A. (2005).
Protein identification and analysis tools on the expasy
server. In Walker, J. M., editor, The Proteomics Pro-
tocols Handbook, pages 571–607. Humana Press.
Huang, G.-B. (2003). Learning capability and storage
capacity of two-hidden-layer feedforward networks.
IEEE Transaction on Neural Networks, 14(2).
Huang, G.-B. and Siew, C.-K. (2004). Extreme learning
machine: Rbf network case. In he Proceedings of the
Eighth International Conference on Control, Automa-
tion, Robotics and Vision (ICARCV).
Huang, G.-B. and Siew, C.-K. (2005). Extreme learning
machine with randomly assigned rbf kernels. Interna-
tional Journal of Information Technology, 11(1):16–
24.
Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2004). Extreme
learning machine: A new learning scheme of feedfor-
ward neural networks. In Proceedings of International
Joint Conference on Neural Networks (IJCNN).
DISULFIDE CONNECTIVITY PREDICTION WITH EXTREME LEARNING MACHINES
13

Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2006a). Ex-
treme learning machine: Theory and applications.
Neurocomputing, 70:489–501.
Huang, G.-B., Zhu, Q.-Y., and Siew, C.-K. (2006b). Real-
time learning capability of neural networks. IEEE
Transaction on Neural Networks, 17(4):251255.
Kabsch, W. and Sander, C. (1983). Dictionary of protein
secondary structure: pattern recognition of hydrogen-
bonded and geometrical features. Biopolymers,
22(12):2577–2637.
Lin, H.-H. and Tseng, L.-Y. (2010). Dbcp: a web server
for disulfide bonding connectivity pattern prediction
without the prior knowledge of the bonding state of
cysteines. Nucleic Acids Research, 38:503–507.
Liu, H.-L. (2007). Recent advances in disulfide connectivity
predictions. Bioinformatics, 2:31–47.
Lu, C.-H., Chen, Y.-C., Yu, C.-S., and Hwang, J.-K. (2007).
Predicting disulfide connectivity patterns. Proteins,
67:262–270.
Martelli, P. L., Fariselli, P., Malaguti, L., and Casadio,
R. (2002). Prediction of the disulfide bonding state
of cysteines in proteins with hidden neural networks.
Protein Engineering, 15(12):951–953.
Mucchielli-Giorgi, M., Hazout, S., and Tuffery, P. (2002).
Predicting the disulfide bonding state of cysteines us-
ing protein descriptors. Proteins, 46:243–249.
Muskal, S., Holbrook, S., and Kim, S. (1990). Prediction
of the disulfide-bonding state of cysteine in proteins.
Protein Engineering, 3(8):667–672.
Nguyen, D. and Widrow, B. (1990). Improving the learning
speed of 2-layer neural networks by choosing initial
values of the adaptive weights. In Proceedings of the
International Joint Conference on Neural Networks,
volume 3, pages 21–26.
Oliphant, T. E. (2006). Guide to numpy.
Pavelka, A. and Proch´azka, A. (2004). Algorithms for
initialization of neural network weights. In Sborn´ık
pr´ıspevku 12. rocn´ıku konference MATLAB, 2:453–
459.
Rubinstein, R. and Fiser, A. (2008). Predicting disulfide
bond connectivity in proteins by correlated mutations
analysis. Bioinformatics, 24(4):489–504.
Serre, D. (2002). Matrices: Theory and applications.
Springer-Verlag New York, Inc.
Shi, O., Cai, C., Yang, H., and Yang, J. (2008). Disulfide
bond prediction using neural network and secondary
structure information. The 2nd International Confer-
ence on Bioinformatics and Biomedical Engineering
(ICBBE).
Song, J.-N., Yuan, Z., Tan, H., Huber, T., and Burrage, K.
(2007). Predicting disulfide connectivity from protein
sequence using multiple sequence feature vectors and
secondary structure. Bioinformatics, 23(23):3147–
3154.
Tamura, S. and Tateishi, M. (1997). Capabilities of a four-
layered feedforward neural network: Four layers ver-
sus three. IEEE Transaction on Neural Networks,
8(2):251255.
Van Rossum, G. et al. (1991). Python language website
http://www.python.org/.
Vincent, M., Passerini, A., Labb´e, M., and Frasconi, P.
(2008). A simplified approach to disulfide connec-
tivity prediction from protein sequences. BMC Bioin-
formatics, 9(20).
Vullo, A. and Frasconi, P. (2004). Disulfide connectivity
prediction using recursive neural networks and evolu-
tionary information. Bioinformatics, 20:653–659.
Zhao, E., Liu, H.-L., Tsai, C.-H., Tsai, H.-K., Chan, C.-
H., and Kao, C.-Y. (2005). Cysteine separations pro-
files on protein sequences infer disulfide connectivity.
Bioinformatics, 21(8):1415–1420.
Zhu, L., Yang, J., Song, J.-N., Chou, K.-C., and Shen, H.-B.
(2010). Improving the accuracy of predicting disulfide
connectivity by feature selection. Journal of Comput-
ing Chemistry, 00(00).
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
14
