A DYNAMICAL MODEL FOR SIMULATING

A DEBATE OUTCOME

A. Imoussaten, J. Montmain

LGI2P, Ecole des Mines d'Alès, Site EERIE Parc Scientifique G. Bresse, 30035 Nîmes cedex, Alès, France

A. Rico, F. Rico

ERIC, Université Claude Bernard Lyon 1, 43 bld Du 11 novembre 69100, Villeurbanne, France

Keywords: Debate, Influence, Decisional power, Choquet integral, Control, Collective decision, Social network.

Abstract: A group of agents is faced with collective decisional problems. The corresponding debate is seen as a

dynamical process. A first theoretical model based upon a muticriteria decision framework was proposed in

(Rico et al., 2004) but without semantic justifications and explicit dynamical representation. A second

descriptive model was proposed in (Imoussaten et al., 2009) where social influences and argumentation

strategy govern the dynamics of the debate. This paper aims at justifying the equations introduced in (Rico

et al., 2004) with the semantics concepts reported in (Imoussaten et al., 2009) to provide a model of a debate

in the framework of control theory that explicitly exhibits dynamical aspects and offers further perspectives

for control purposes of the debate.

1 INTRODUCTION

A group of agents is faced with a collective decision.

A debate is organized to identify which alternative

appears to be the most relevant one after

deliberation. This study is limited to the binary but

common situation where two options

1±

are

involved. It is assumed that each agent has an

inclination to choose one of both alternatives

1±

which, due to influence of other agents, may be

different from the decision of the agent (Grabisch

and Rusinowska, 2008). More generally, it can be

considered that each time a speaker intervenes in the

debate, agents may change their preference due to

social influences in the group. When agents’

preferences do not change anymore, the deliberation

process ends and a group decision is made. The aim

of the debate is that every agent knows the

arguments of all the others at the end of the

deliberation process and makes his final decision

with full knowledge of the facts.

The deliberation is seen as a dynamical process

with its own dynamics where beliefs and preferences

of agents evolve when arguments are exchanged.

The deliberation outcome thus depends on the order

the agents intervene in the debate to explain their

opinion and on the influence an agent may exert on a

social network.

Social influence is here related to statistical

notion of decisional power of an individual in a

social network as proposed in (Hoede and Bakker,

1982) and (Grabisch and Rusinowska, 2008).

One of the conclusions of (Grabisch and

Rusinowska, 2008) concerns the integration of

dynamical aspects in the influence model. Indeed,

the authors’ framework is a decision process after a

single step of mutual influence. In reality, the mutual

influence does not stop necessarily after one step but

may iterate. This paper proposes a possible

extension of (Grabisch and Rusinowska, 2008) in

the dynamical case. The evolutions of agents’ beliefs

during the debate change or reinforce the agents’

convictions relatively to their initial preference.

Intuitively, among others, the social influence of an

agent depends on the more or less marked

convictions of the other agents. Thus, the idea is to

define influence as a time-varying variable itself in

our model.

(Rico et al., 2004) introduces the concepts of

influence and conviction in the simulation of a

debate. This article follows prior works proposed in

(Bonnevay et al., 2003). In (Rico et al., 2004),

Imoussaten A., Montmain J., Rico A. and Rico F..

A DYNAMICAL MODEL FOR SIMULATING A DEBATE OUTCOME .

DOI: 10.5220/0003126400310040

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 31-40

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

coalitions of agents are modeled with capacities; the

change of conviction during the debate was

computed with a symmetric Choquet integral which

is an aggregation function usually used in

multicriteria decision making (Grabisch and

Labreuche, 2002). The main drawback in (Rico et

al. 2004) is its lack of semantic justifications.

Thus, (Grabisch and Rusinowska, 2008) provides

a formal framework to define the notion of influence

and (Rico et al., 2004) introduces the revision

equations of agents’ convictions and preferences.

Finally, (Imoussaten et al., 2009) suggests a

cybernetic interpretation to merge both models. This

paper is the continuation of (Rico et al., 2004) in the

light of (Imoussaten et al., 2009). The main

contribution of this paper is to propose the state

equations of the cybernetic interpretation to describe

the way agents’ convictions may evolve in time. To

achieve this goal, a capacity is introduced to model

the relative importance of agents in the debate that is

based upon the decisional power of agents using the

generalized Hoede-Bakker index (Grabisch and

Rusinowska, 2008), (Hoede and Bakker, 1982).

Hence some simulations are proposed to illustrate

the collective decision making process.

The paper is organized as follows. Section 2

recalls briefly the main concepts of models in (Rico

et al., 2004) and (Grabisch and Rusinowska, 2008).

Based upon this formal framework, section 3

establishes the state equations that model the

dynamical relationships between convictions and

influences when a pair of speaker-agent, listener-

agent is isolated. Section 4 associates the revision of

convictions and the changes of preferences. Section

5 proposes some illustrations. Finally, the

conclusion evocates the use of the model for debates

controlling purposes.

2 CONCEPTS AND NOTATIONS

2.1 Notion of Influence in a Debate

The assumption behind our model is that the

influence of an agent is related to his capacity to

alter the group decision. It evocates the concept of

«weight» of an agent’s choice in a collective vote

procedure. This «weight» cannot be a static

parameter, because it should evolve with the

preferences of agents that make the formation of

certain coalitions more probable than other ones. To

tackle this issue the definition of decisional power as

proposed in (Grabisch and Rusinowska, 2008) is

first summarized.

We consider a set of agents denoted

{ ,..., }

{1,..., }N

to simplify the notations and the power set

is denoted

{ ,..., }

. It is assumed that each agent has

an inclination to choose +1 or -1 which, due to

influence of other agents, may be different from the

decision of the agent. The point of departure is the

concept of the Hoede-Bakker index⎯the notion

which computes the overall decisional ‘power’ of an

agent in a social network (

agents). This index was

provided in 1982 (Hoede and Bakker, 1982).

Definition:

the Hoede-Bakker index of agent

defined by:

{/ 1}

(, ) . ( )

GHB B gd gd Bi

−

∑

(1)

•

is an inclinations vector in

{1, 1}

I =− +

that

models the agents’ inclinations, more precisely, we

have

( ,..., )

ii i=

where

{1, 1}

i ∈− +

the

jth−

coordinate of

is the inclination of the agent

•

II→

is the influence function and for any

inclination vector

the decision vector

is a n-

vector consisting of ones and minus ones and

indicating the decisions made by all agents.

•

:() {1,1}gd B I →− +

is the group decision

function, having the value +1 if the group decision is

+1, and the value −1 if the group decision is −1.

The main drawback of the Hoede-Bakker index

is that it hides the actual role of the influence

function, analyzing only the final decision in terms

of success and failure. The decision is successful for

an agent as soon as his inclination matches the group

decision.

In (Grabisch and Rusinowska, 2008), the authors

separate the influence part from the group decision

part, and propose a first modified index of decisional

power where the decision of the agent must coincide

with the group decision to be a success for the agent.

Lastly, the authors provide a second modified

decisional power, which allows the inclinations

vectors to be unequally probable.

Definition:

Let

:[0,1]pI→

be a probability

distribution,

()pi

is the probability

occurs. The

modified decisional power is then:

{/( ) 1}

(, , ) (). ( )

(). ( ).

iBi

gd p p i gd Bi

pi gd Bi

=−

−

∑

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

To conclude this summary, for each agent

the

probabilities of success and failure are reminded:

{ /() ()}

(, , ) ()

bI b gdb

SUC B gd p p B b

−

∈=

∑

{/() ()}

(, ,) ()

bI b gdb

AIL B gd p p B b

−

∈=−

∑

Note that we have

(, ,) (, ,) (, ,)

jjj

aaa

B gd p SUC B gd p FAIL B gd p

=−

2.2 Convictions and Preferences in a

Debate

This section presents the dynamical model of the

debate proposed in (Rico et al., 2004). The influence

an agent may have on the others is modeled by a

capacity over

{ ,..., }

Definition: A capacity

over

{ ,..., }

is a set

function

{,..., }

:2 [0,1]

→

such

that

() 0

∅=

({ ,.., }) 1

and

,'AA∀⊆

{,.., }

'()(')

AAA

υυ

⊆ ⇒ ≤

The profile of an agent

includes his preference,

his importance (his capacity

()

), his conviction

[0,1]

c ∈

related to his preference. It is stated as a

rule that agents speak in turns. The agent

(speaker-agent) who speaks and any agent

(listener-agent) are isolated which introduces a

capacity

upon the pair of agents

(, )

. More

precisely, the following capacity is defined

()

(, )

aa l

()

(, )

aa s

and

(, ) 1

aa l s

The change of conviction is then modeled with

the symmetric Choquet integral also called Sipos

integral. The definition of Choquet integral and

Sipos integral are now provided.

Definition: Let

( ,..., ) [0,1]

cc c=∈

be a vector of

convictions, () be a permutation on

{1,..., }N

such

that

(1) ( )

...

cc≤≤

and

be a capacity on

{ ,..., }

The Choquet Integral of

with respect to

defined by:

() ( 1)

({( ),..., ( )})() .

iNCc c c

−

⎡⎤

=−

⎣⎦

∑

with

(0)

c =

Definition: Let

( ,..., ) [ 1,1]

cc c=∈−

be a vector

which can take negatives values, () be the

permutation on

{1,..., }N

such that

(1) ( ) ( 1) ( )

... 0 ...

pp N

aaa a

ccc c

≤≤ ≤≤ ≤≤

and

be a

capacity on

{ ,..., }

The symmetric Choquet Integral of

with respect to

is defined by:

() ( 1) ( )

(1) () ( 1)

( ) ({(1),..., ( )}) ({( ),..., ( )})

({( 1),..., ( )}) ({( ),..., ( )})

ii p

p ii

aa a

aaa

Cc c c i c i p

cp N cc iN

υυ

+ −

−

=− +

++ +−

⎡⎤

⎣⎦

⎡⎤

⎣⎦

∑



In this paper the Sipos integral is defined on the set

of agents

{, }

. It is denoted

,aa



. The changes

of convictions proposed in (Rico et al., 2004) can be

summarized as follows with

,aa



- If agents

and

have the same preference,

When

cc>

the new conviction is:

(,) ( ). ()

aa s l l s l l s

aa a a a aa s

Ccc ccc a

=+ −



When

cc>

the new conviction is:

(,) ( ). ()

aa s l s l s l s

aa a a a aal

Ccc c cc a

=+ −



- If agents

and

do not have the same

preference, the new conviction is:

(,) . () . ()

aa s l s l s l l s

aa aaa s aaa l

Ccc c ac a

υυ

=− +



The main drawback to this model is its lack of

semantics justifications with regard to capacity

(influence is merely a normalized relative

importance), the concept of conviction is not

formally defined and the revision equations are not

provided in an appropriate formalism where time

would appear explicitly (dynamical aspects).

3 THE DYNAMICAL MODEL

This section presents our dynamical model for

simulating a debate outcome. To begin note that in

the framework of this paper, influence function

used in (Grabisch and Rusinowska, 2008) is

perceived as a disturbance function applied to the set

of all the possible inclination vectors.

A DYNAMICAL MODEL FOR SIMULATING A DEBATE OUTCOME

3.1 Decisional Power and Capacities

This section proposes to design a capacity based

upon the decisional power for the above model.

For any

iI∈

, the group decision is modeled by

()

dBi

and belongs to

{1, 1}−+

Furthermore,

(, , ) [1,1]

Bgd p

∈−

- If the decisional power of an agent is close to

1−

, it

means that the agent scarcely chooses the alternative

the collective finally chooses: he fails most of the

time (

FAIL

- In revenge, when his decisional power is close to 1,

the agent is most of the time successful

()SUCC

;

his decisional power is high.

For example, without further information, the

importance of an agent

, i.e., his capacity

()

can be defined as:

() (, ,)

aBgdp

υφ

()[0,1]

∈

with

() 0

if and only if

(, , ) 1

Bgd p

=−

and

()1

if and only if

(, ,) 1

Bgd p

It thus defines a function

:{ ,.., } [0,1]

→

From this function, a capacity

can be generated

over

{ ,.., }

, with constraints

,'AA∀⊆

{,.., }

'()(')

AAA

υυ

⊆ ⇒ ≤

. Without further

knowledge, it can be chosen:

() max( ), {,.., }

aAaa

υυ

∈

=∀⊂

and

({ ,.., }) 1

Note that this definition does not necessarily

imply that there exists an agent whose capacity is

equal to 1.

In the following and to simplify notations, such a

capacity is denoted

for a decisional power

(, ,)Bgd p

. The decisional power of individuals

on which

{ ,.., }

:2 [0,1]

→

is based measures the

cases where the final decision of

matches the

group decision. An agent with a high decisional

power is expected to bring several agents round and

thus the decisional power is considered as an

estimation of his “influence” in the group; although

it is not an influence index in the sense of (Grabisch

and Rusinowska, 2008).

3.2 Time-varying Probabilities

Note that this subsection is dedicated to the design

of probability

as a time-varying function. It is

thus supposed that convictions vectors

()ck

(the

convictions vector of the agents w.r.t alternative

at time

) and

'( )ck

(the convictions vector of the

agents w.r.t alternative

1−

at time

) are known at

k. Their computation is provided in the next section.

The model proposed in this paper is based upon

the extended decisional power in (Grabisch and

Rusinowska, 2008) that allows the inclinations

vectors to be unequally probable. The definition of

the associated probability distribution

:[0,1]pI→

is now required (see section 2.1). This paper

proposes to base the probability computation upon

the convictions of agents with regard to the

alternatives.

The conviction of an agent regarding an

alternative is related to the probability this agent

chooses this alternative, i.e., the probability of his

inclination as defined in (Grabisch and Rusinowska,

2008). As stated above, convictions evolve in time

during the deliberation process.

()

() (),.. , (), ..., ()

aa a

ck c k c k c k=

where

()

is the conviction of agent

w.r.t alternative

time

'' '

'( ) (c ( ),... ,c ( ), ...,c ( ))

aa a

ck k k k=

where

()

is the conviction of agent

w.r.t alternative

1−

time

Let

iI∈

be an inclinations vector, and let define

() [0,1]

ck∈

as an “average” conviction at time

for

: this value summarizes the distributions of

agents’ convictions in

()

is an

«aggregated conviction» of the group of agents for

. This aggregation should take into account relative

importance of agents and their interactions.

The probability is built by recurrence on k.

At time k = 0:

()

(0) (0),... , (0), ..., (0)

aaa

cc c c=

is the a priori convictions vector of agents.

(0) [0,1], 1..

cjN∈=

is the a priori convictions

, and it is also the probability of his conviction.

Initially (

0k =

), if

is the preference of

then

the probabilities of the agent

regarding his

preference and the other alternative are:

(()[ 0] 0)

jj j

aa a

pi k c==

and

( )[0] 1 (0)

jj j

aa a

pi c−=−

Before the debate starts, the inclination of each agent

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

does not depend on the social network. Then, the

probability distribution associated to a priori

probabilities is the product of the individual

probabilities

0k =

,()[0] ( )[0]

jaa

iIpi pi

∀∈ =Π

. It is thus possible:

computing the decisional power for any agent

0k =

(, ,[0])

Bgd p

;

- computing the capacity

[0]

over

{ ,.., }

for

1k =

as proposed in subsection 3.1.

At time k = 1

Capacity

[0]

allows computing

(1)

, the

aggregated conviction at

1k =

for the inclinations

vector

. The relative importance of agents and of

their coalitions is taken into account in the

aggregation model of

through a Choquet integral.

Let

iI∈

be an inclinations vector. Each

coordinate

is one of the alternative

1−

. For

agent

(1)

is the conviction

associated to his preference. A conviction vector

()

(1) (1) ... (1)

cc c=

is associated to each

inclinations vector

, where for any

(1)

. The synthetic conviction of the

group for inclination

at time

1k =

is computed

with a Choquet integral defined upon

[0]

(1) ( (1), ..., (1)) [0,1]

cCc c

=∈

A probability at

1k =

can then be defined:

(1)

()[1]

(1)

∈

∑

It is now possible:

- Computing the decisional power of any agent

1k =

(, ,[1])

Bgd p

;

- Computing the capacity

[1]

over

{ ,.., }

for

2k =

as proposed in subsection 3.1.

More generally, at time k + 1:

Capacity

[]k

computed at

allows

computing

(1)

ck+

, the aggregated conviction at

1k +

for inclinations vector

with the Choquet

integral:

[]

( 1) ( ( 1),..., ( 1))

ka a

ck C c k c k

+= + +

Then, probability at time

1k +

is defined as:

(1)

()[ 1]

(1)

pi k

∈

∑

It is now possible computing

(, ,[ 1])

Bgd pk

and

[1]k

The probability required by the extended model

of decisional power has been designed as a time

varying variable because it evolves with the agents’

convictions. Therefore,

(, ,[])Bgd pk

evolves in

time too. This principle seems rather intuitive

because it corresponds to the idea that the social

influence of an agent depends on the more or less

marked convictions of the other agents when he

speaks.

3.3 Conviction State Equations

The aim of this section is to establish the state

equations that model the dynamical relationship

between convictions and influences. Let consider a

pair of listener-agent, speaker-agent denoted

and

. Their convictions for the alternative

are

()

and

()

, respectively,

()

and

()

for the alternative

1−

Two variables are necessary to model the

rhetoric quantity that is exchanged between both

agents

and

The difference of convictions between both agents;

- The relative importances of agents

and

modeled by capacities

[]( )

and

[]( )

Four rhetoric exchanges are distinguished. These

four situations are presented in the case when

prefers alternative

. Then, there exist two sub

cases for agent

: his favorite alternative is the one

or the opposite one. Each case can be divided

again into two sub cases:

’s conviction is greater

than (respectively lower than)

’s conviction.

When agent

prefers the alternative

1−

convictions

take the place of convictions

in the

formula: the equations that appear in the

computation of

(1)

ck+

when both agents have the

same preference are the same ones to compute

(1)

ck+

in case of opposite preferences and vice

versa.

Synergic Exchange

It is the case when the preference of the agent

reinforced by the intervention of the agent

who

resolutely looks on the same alternative in favor.

The conviction of the agent

increases. The

increase is proportional to the difference between

A DYNAMICAL MODEL FOR SIMULATING A DEBATE OUTCOME

both convictions and to the capacity of speaker

This situation corresponds to the case when

and

have the same preference and moreover

cc>

. The intuitive difference equation is then

(Figure 1):

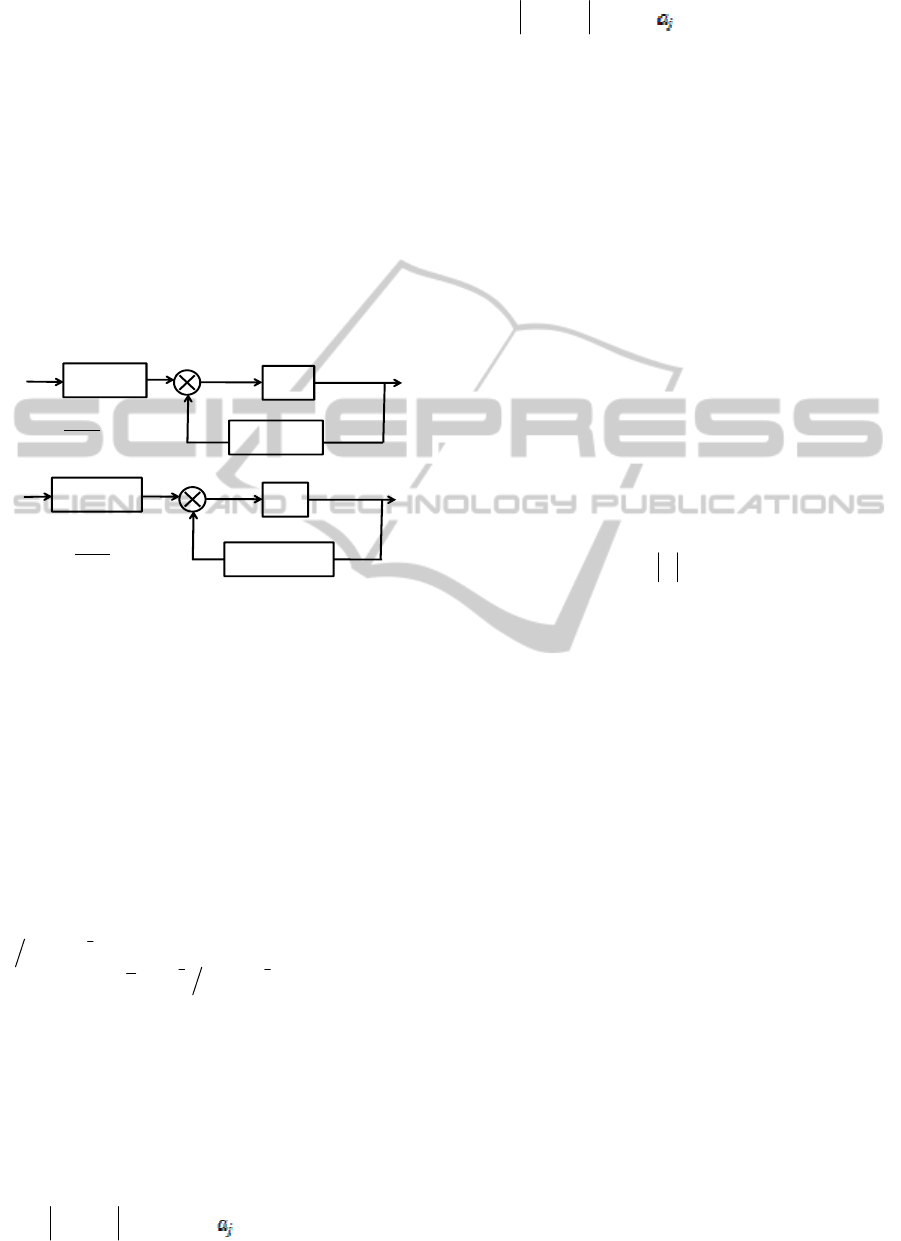
( 1) ( ) ( ( ) ( )). [ ]( )

llsl

aaaa s

ck ck ck ck ka

+− = −

( 1) () ( () ()). []( )

llsl

aaaa s

ck ck ck ck ka

+= + −

()

∫

[]( )

Figure 1: Synergic Exchange.

Revisionist Exchange

The agent

understands the argument of the

agent

, who has the same preference but more

moderately.

appears to speak with restraint from

point of view

and

’s

doubt appears.

’s

conviction is thus mitigated by

intervention. This

situation corresponds to the case when

and

have the same preference and moreover

cc>

The intuitive difference equation is then (Figure 2):

( 1) () ( () ()).(1 []( ))

llls

aaaa l

ck ck ck ck ka

+− =− − −

( 1) () ( () ()). []( )

lsls

aaaa l

ck ck ck ck ka

+= + −

The agent

observes the indecision

agent

who nevertheless shares his opinion:

contributes to

’s

doubt. The conviction

decreases due to

’s intervention that is

proportional to

(1 [ ]( ))

−

on one hand (lack of

assurance of

related to his social position in the

group) and to the difference between both

convictions of agents

and

on the other hand.

∫

1[]()

−

1[]()

−

()

Figure 2: Revisionist exchange.

Antagonist Exchange

Both agents do not share the same preference;

agent

nevertheless understands the advantages of

preference. A convincing intervention of

may

contribute to make

doubtful whereas a non

persuasive intervention may strengthen his

preference on the contrary.

(1 ( ))

ck−

is a measure of

‘s hesitation and

provides

with an estimation of the strength of

’s

opposition. According to the strength of this

hesitation, the previous difference equations are

usable with

(1 ( ))

ck−

and two situations are to be

distinguished (Figure 3).

A too weakly marked preference of

means a

weak opposition from

point of view and

reinforces

‘s opinion.

‘s conviction should then

increase.

The intuitive difference equation is then

(synergic exchange with

(1 ( ))

ck−

Case 1:

cc−≥

(1)()((1())()).[]()

ll sl

aa aa s

ck ck ck ck ka

+− = − −

(1) ()(1 () ()).[]()

ll sl

aa aa s

ck ck ck ck ka

+= +− −

In the second case,

‘s conviction decreases after

’s intervention (revisionist exchange with

(1 ( ))

ck−

Case 2:

cc−<

( 1) () ( () (1 ())).(1 []( ))

lll s

aaa a l

ck ck ck ck ka

+− =− −− −

(1)(1 ())(() ()1).[]()

lsls

aaaa l

ck ck ck ck ka

+= − + + −

All these different types of exchanges can be

synthesized with a Sipos integral as follows:

The agents

and

have got the same preference:

( 1) [ ]( ( ), ( ))

lsl

aaa

ck Ckckck



The agents

and

do not share the same

preference:

( 1) [ ]((1 ( )), ( ))

lsl

aaa

ck Ck ck ck

+= −



To conclude this part, the decisional power

provides a semantic interpretation for the capacity

in the recurrence equations in (Rico et al., 2004),

conviction is here related to the probability an agent

will choose an alternative rather than the other one

(probability distribution over inclinations vectors).

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Thus, the model in (Rico et al., 2004) becomes

interpretable in games theory framework (Grabisch

and Rusinowska, 2008). Revision equations of

conviction appear as inputs-outputs balances

according to alternatives assessment. Introducing

time in the equations of (Rico et al., 2004) implies

that revision equations of conviction are now seen as

state equations of agents’ mental perception. This

new interpretation provides a semantics for the

model of a debate in (Rico et al., 2004): it is related

to the notions of influence and decisional power as

proposed in (Grabisch and Rusinowska, 2008) with

a formalism close to the one of dynamical models in

control theory as suggested in (Imoussaten et al.,

2009).

()

∫

[]( )

(1 ( ) )

ck−

Cas 1

∫

1[]()

−

1[]()

−

()

Cas 2

(1 ( ) )

ck−

Figure 3: Antagonist exchange.

4 PREFERENCES CALCULUS

This section presents how to compute the preference

during the debate.

Initially each agent

assesses both alternatives

and

1−

with a score in

[0,1]

. These assessments

are noted

and

−

. It is then possible to build

initial preferences and convictions:

prefers alternative

with the highest score,

’s conviction related to alternative

()

jjj

aaa

nnn+

and

’s conviction related to the

other alternative

()

jjj

aaa

nnn+

Preferences changes depend on the way convictions

evolve in time. For any agent

, it is supposed

there exists a threshold

such that when the

difference between two convictions is below this

threshold then the agent

cannot have a

preference. The threshold value may be

characteristic of each agent. To summarize:

- When

jj j

aa a

−<

, then

has no preference;

- When

jj j

aa a

−≥

prefers the alternative

with the highest conviction.

Finally, an agent without preference cannot

intervene is stated as a rule of the debate.

5 ILLUSTRATION

5.1 Simulations of the Debate’s

Outcome

In order to illustrate the principle of the above

dynamical representation of a debate, the four

following elementary models for influence function

have been implemented:

•

is the identity that is to say for any inclination

vector i we have

ii=

•

is the opposite of identity, for any inclination

vector i we have

ii=−

•

is a mass psychology effect function. More

precisely, if we denote

{/}

ikNi

=∈ =

satisfy : for each

iI∈

,()itthenBi i

εεε

>⊇

where

[1, ]tn∈

and

=±

•

is a majority

•

influence function models behaviors of type: if a

majority of agents has an inclination +1, then all

agents decide +1; if not, all agents decide −1

For the four cases, the group decision function

is a mere majority and a basic capacity is designed

as proposed in section 1.3.

Let consider a group of

8N =

agents. The initial

convictions of agents relatively to both alternatives

are considered as variates: 50 random drawings of

these 8 initial probabilities are carried out (Figure 4).

For each of these 50 initial convictions vectors the

order the agents intervene in the debate is then

considered: 200 permutations are randomly selected

(among the

possible rankings) for each initial

convictions vector.

Each of the four elementary illustrations is

plotted in figure 4 (one for each

function). For

each of the 50 initial convictions vectors randomly

selected, a bar represents the number of outcomes

1±

(light-grey for

and dark-grey for

1−

To each of these figures is associated the

maximal number of rounds that have been necessary

to achieve the ground decision for each initial

convictions vector. In the proposed simulations this

number does not exceed 8 rounds in any

-case.

A DYNAMICAL MODEL FOR SIMULATING A DEBATE OUTCOME

The indifference threshold is

0.01

for any

agent. Agents speak in turns according to the order

induced by the 200 permutations on condition they

have a clear opinion: an agent

can speak if

−≥

For a same initial convictions vector it can be

observed that for each function

, the outcome of

the debate may depend on the order the agents

intervene. This type of situation can be interpreted as

weakly marked preferential contexts where any

perturbation can change the debate’s outcome. From

this point of view, influence function

is a

disturbance function in this dynamical model of a

debate. As a consequence, simulations allow

checking that the order the agents intervene in the

debate and their influence are decisive variables with

regard to the convergence of conviction state

equations.

The social influence of an agent may thus be

considered as a disturbance in the deliberation

process except if it is relevantly used by the debate

manager to govern the discussion. Indeed, in this

later case, social influence can be envisaged as an

actuator that enables controlling the outcome of the

debate or at least accelerating its convergency. For

example, when the outcome of the debate is quasi

certain (the bar is almost completely light or dark

grey), then the simplest control could consist in

choosing the order the agents intervene that

minimizes the maximal number of rounds. More

complex control can be clearly envisaged but the

aim of this paper was merely to propose a dynamical

model of the debate in a framework close to control

theory representations, then control techniques

should be naturally implemented in the future.

5.2 Debate as a Decision Making

Process

This part presents a potential application of the

presented dynamical model. The aim is to use it as

a vote system. More precisely, in this example, both

alternatives

1− and 1+ are not considered to be

equivalent: +1 is the right decision while -1 is

associated to an error. This situation may occur in

classification problems when the agents are

competitive classification algorithms.

The agents are expected to provide the right

answer most of the time but they usually disagree on

singular cases. A common solution is to use a voting

process to achieve a group decision. For example, let

the agents be 7 different classification algorithms

whose success rates are respectively: 0.6, 0.7, 0.8,

0.8, 0.6, 0.7 and 0.6; then, the group success rate

using normal vote is 0.86. Even when a weighted

vote is introduced, the same rate is obtained because

of the value of the Shapley–Shubik power index

(Shapley, 1953) which is equal to 1/7 for any

classification algorithms. Indeed as probability are

hardly, bigger than 50% for each classification

algorithms, for the normal vote as for the weighted

vote the chosen value is the one which is chosen by

at least four agents. This effect does not take place

in the proposed method because the least agents are

also the ones who change most easily his point of

view. More precisely, this issue can also be tackled

with our debate model with identity as

function,

and success rates for convictions. It is supposed that

7 competitive classification algorithms are available

and that the right solution is supposed to be

alternative +1. The initial probability of the 7

algorithms to choose the alternative +1 are: 0.6, 0.7,

0.8, 0.8, 0.6, 0.7 and 0.6. Moreover it is supposed

that 10 000 cases are studied by each agent. For each

case, the answer of the agent is inferred according to

his probability to be right ( this is one method to

model the aggregation function corresponding to the

different classification algorithm. Then, for each of

the 10000 cases, the choice with a majority vote

procedure and the collective decision achieved with

our model when convictions at the start are the

initial probabilities are both computed. The program

stops when all the classification algorithms do agree.

While simple and weighted majorities obtain the

right answer with a rate of 86 %, our method rate is

94 %.

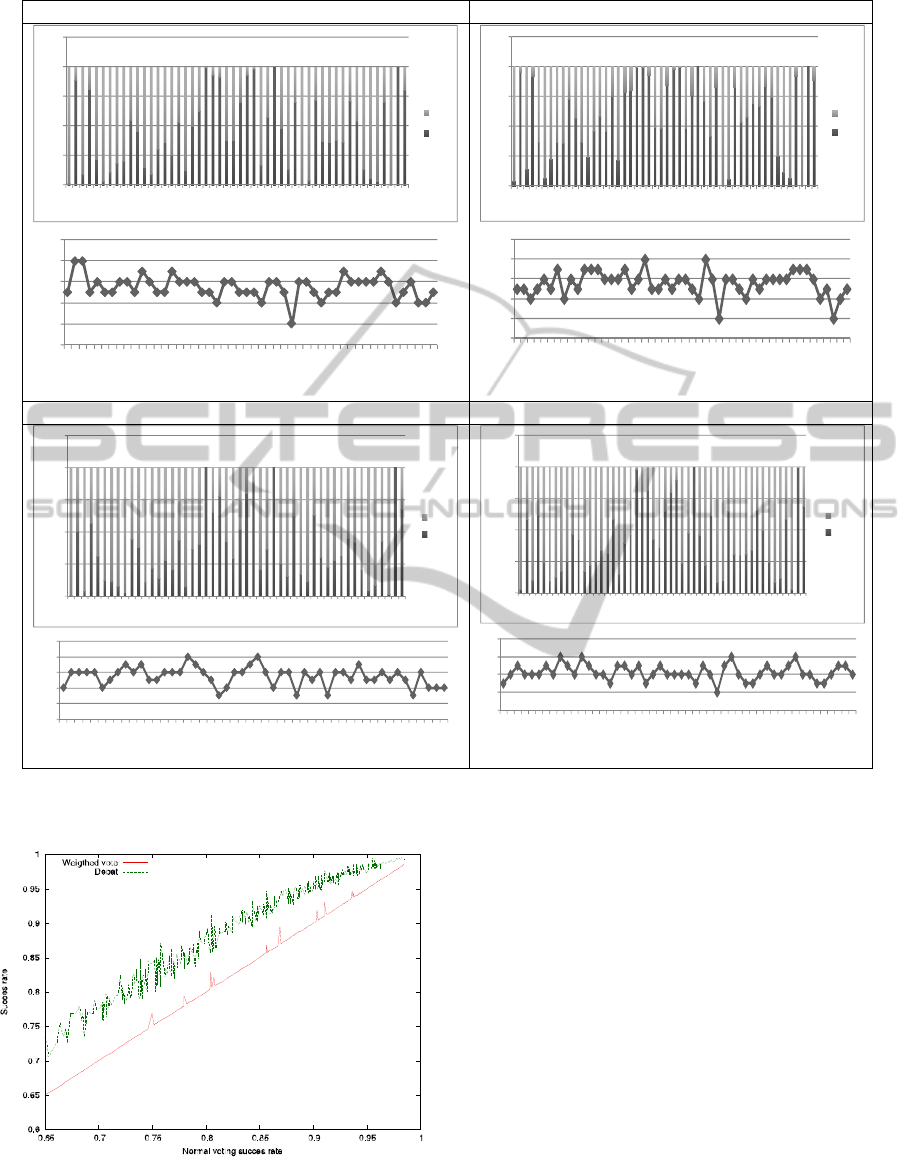
For 7 agents, several values of probability to

make the right decision are randomly generated and

3 rates are computed:

- the rate of success of the vote,

-the rate of success the weighted vote,

- the rate of success of our debate.

The rate of the weighted vote and of our debate

according to the rate of simple vote are plotted in

figure 5. Note that the same rate for the simple vote

can be obtained with very different sets of

probabilities. That is why the rate of success of the

weighted vote is somewhat equal to the simple vote

for very particular sets of probabilities where several

agents (algorithms) are much better than the others.

The debate always gives a better rate but its

preferences change according to the profile of

involved probabilities.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

B := Identity B := -Identity

100

150

200

250

135791113151719212325272931333537394143454749

"+1"

"-1"

1 3 5 7 9 1113151719212325272931333537394143454749

100

150

200

250

1 3 5 7 9 1113151719212325272931333537394143454749

"+1"

"-1"

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49

B := Majority B := Mass Psychology Effect

100

150

200

250

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49

"+1"

"-1"

1 3 5 7 9 1113151719212325272931333537394143454749

100

150

200

250

135791113151719212325272931333537394143454749

"+1"

"-1"

135791113151719212325272931333537394143454749

Figure 4: Simulations of the debate outcomes (50 initial convictions; 200 permutations).

Figure 5: Simulations―weighted vote and debate.

6 CONCLUSIONS

AND PERSPECTIVES

The state equations that have been established in this

paper allow simulating macroscopically the outcome

of a debate according to the initial inclinations of

agents and the social influences in the group (the

influence function is a priori known). The

deliberation outcome depends on the order the

agents intervene in the debate to explain their

opinion and on the influence an agent may exert on a

social network.

The formalism of the model that is proposed in

this paper is close to the one used in control theory

to model dynamical behaviors of technical systems.

Governing a debate could then be seen as a control

problem whose aim could be, for example, how to

A DYNAMICAL MODEL FOR SIMULATING A DEBATE OUTCOME

reach as quick as possible a consensus or how to

reinforce one alternative rather than the other one,

etc.

A debate is thus seen as continuous dynamical

system: a state equations representation has been

preferred to the muticriteria decision-making

framework in (Rico et al., 2004) because time

explicitly appears in revision of convictions. The

model semantic is also inspired of games theory

concepts proposed in (Grabisch and Rusinowska,

2008): influence and decisional power in a social

network. In our dynamical extension, the decisional

power is a time-varying variable itself and can be

used as the actuator signal in the control loop of

debate. The state equations system established in

this paper allow stochastically simulating the

outcome of a debate and effects of a control strategy

on this issue.

One possible application of this model is

obviously simulating a debate’s outcome in order to

obtain some indications about the final collective

decision. When simulations are performed for a

great number of initial agents’ convictions and of

speaker intervention rankings, the probability the

outcome is

1± can be estimated. Hence, the

dynamical influence model can be used to make the

debate outcome more certain (it may appear as a

dishonest method when agents are human beings but

as a relevant technique when agents are artificial

agents such as sensors or classifiers) or modify the

convergence dynamics of the debate.

REFERENCES

Bonnevay, S., Kabachi, N., Lamure, M and Tounissoux,

D., 2003, A multiagent system to aggregate

preferences. In IEEE International Conference on

Systems, Man and Cybernetics, pages 545-550,

Washington, USA.

Grabisch, M. and Labreuche, C., 2002. The symmetric and

asymmetric choquet integrals on finite spaces for

decision making. Statistical paper, Springer Berlin /

Heudelberg, vol. 43, 2002 pp 37-52.

Grabisch, M. and Rusinowska, A., 2008. A model of

influence in a social network. Business and

Economics. s.l.: Springer Netherlands.

Grabisch, M. and Rusinowska, A., 2009. Measuring

influence in command games, Social Choice and

Welfare 33: 177-209.

Hoede, C, Bakker, R., 1982. A theory of decisional power.

Journal of Mathematical Sociology, 8:309-322.

Imoussaten, A., Montmain, J. et Rigaud, E., 2009.

Interactions in a Collaborative Decision Making

Process: Disturbances or Control Variables?.

COGIS’2009, Paris.

Rico, A., Bonnevay, S., Lamure, M., Tounissoux, D. A,

2004. Debat modelisation with the Sipos integral.

LFA’2004, Nantes.

Rusinowska, A. and De Swart, 2007. On some properties

of the Hoede-Bakker index. Journal of Mathematical

Sociology 31: 267-293.

Shapley, L. S., 1953. A Value for n-Person Games. in H.

Kuhn and A. Tucker (Eds.), Contribution to the

Theory of Games, vol. II, number 28 in Annals of

Mathematics Studies Princeton, pp. 303-317.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence