CHAOS LEVEL INVESTIGATION OF CENTRE-OF-PRESSURE
SINGLE-STEP DISPLACEMENT IN STATIC AND DYNAMIC
VISUAL CONDITIONS
Lili Pei
1,2,3
, Shujia Qin
1,2
, Wei Ding
1,2
, Lei Miao
1
and Hongyi Li
1
1
State Key Laboratory of Robotics, Shenyang Institute of Automation Chinese Academy of Sciences, Shenyang, China
2
Graduate School of Chinese Academy of Sciences, Beijing, China
3
College of Physics and Electronics, Shanxi University, Taiyuan, China
Keywords: Postural control, Centre-of-pressure, Visual condition, Entropy.
Abstract: As a convenient and feasible measure of postural control, centre-of-pressure (CoP) trajectories are investi-
gated in most of postural research. The characteristics extracted from CoP trajectories provide valuable
evidences in nature explorations of postural control. In this research, Shannon entropy is introduced into
CoP trajectories analysis to reveal random characteristics of human upright postural control. In our Shannon
entropy analysis, chaos level of CoP single-step displacement is inspected in static and dynamic visual
conditions. Experimental results from twenty-one subjects under four visual conditions indicate that human
postural control in upright stance appears more regulated in direction control than in amplitude control. This
conclusion has specific significance in postural experiment design and postural control improvement.
1 INTRODUCTION
Postural control is widely investigated in posture-
related realms, such as balance assessment, motion
analysis, disease rehabilitation and elderly or dis-
abled assistance. Numerous researchers performed
their explorations of postural control through signal
analysis (Rougier, 1999), model simulation (Hide-
nori & Jiang, 2006) and sense-influence investiga-
tion (Rougier, 2004). Although these researchers
have made many achievements, current investigation
into postural control is still far from completion.
Sense-influence investigators care about visual,
vestibular, and proprioceptive influence on postural
control. These researchers inspect subjects’ postural
responses by manipulating postural environments.
Bronstein (1986) studied visually evoked postural
response by positioning subjects on an earth-fixed
force platform inside a movable room. Mergner
(2005) and his cooperators placed subjects on a rota-
tional force platform inside a rotational cabin to ex-
plore the visual induced postural saturation.
Other investigators focus their efforts on postural
data analysis and model simulation. As a measure of
posture, displacements of centre-of-pressure (CoP)
are largely analyzed in postural control research.
The CoP is the point location at which the vertical
ground reaction force is applied. Collins and De
Luca (1993) analyzed CoP trajectories of upright
stance and presented a stabilogram-diffusion plot.
Based on the plot, the researchers suggested that
open-loop and closed-loop control schemes were
utilized by the postural control system over different
time intervals. Peterka (2000) demonstrated similar
plots through simulation with a purely closed-looped
control model. Therefore, Peterka (2000) hypothe-
sized that a nonlinear open-loop operation might be
unnecessary for upright stance maintenance.
In our research, Shannon entropy is introduced
into the analysis of CoP trajectories in order to re-
veal random characteristics of human upright pos-
tural control. With the entropy analysis, CoP single-
step displacements are investigated both in ampli-
tude and deflection angle. Furthermore, static and
dynamic visual conditions are designed to confirm
the validity of our findings.
2 METHODS
Upright stance in two static (S1 and S2) and two
dynamic (D1 and D2) visual conditions is examined
262
Pei L., Qin S., Ding W., Miao L. and Li H..
CHAOS LEVEL INVESTIGATION OF CENTRE-OF-PRESSURE SINGLE-STEP DISPLACEMENT IN STATIC AND DYNAMIC VISUAL CONDITIONS.
DOI: 10.5220/0003126702620265
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 262-265
ISBN: 978-989-8425-36-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

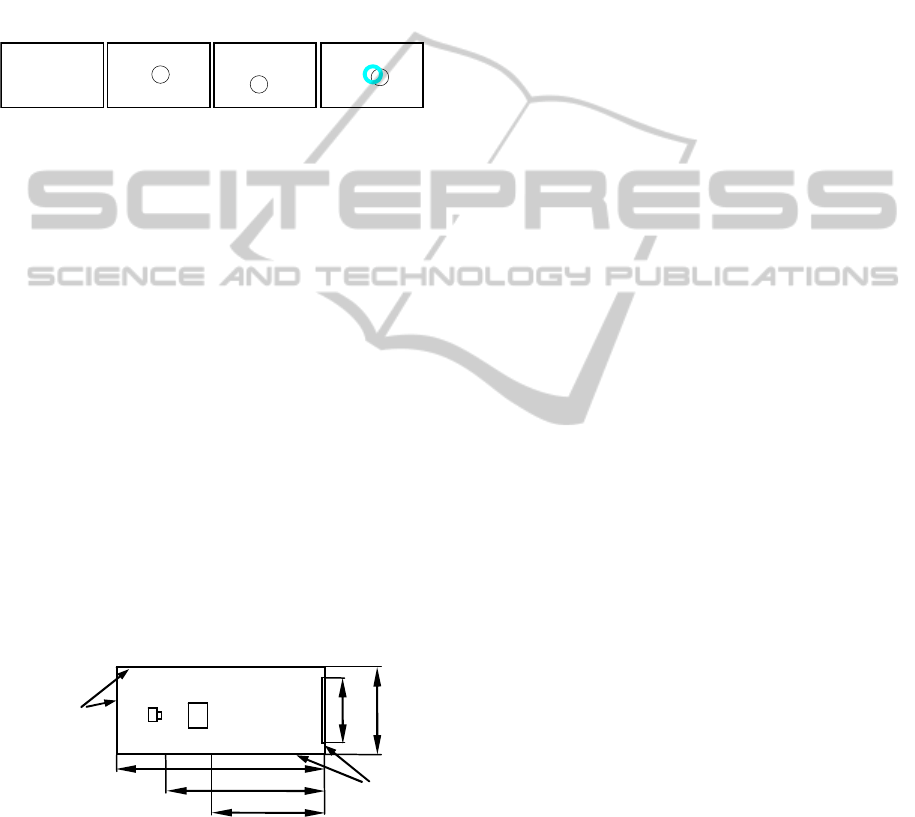
in this study. As Figure 1-a shows, the first visual
scene (in S1) displays a stationary black background;
as Figure 1-b indicates, in the second scene (in S2),
a stationary white spot is added in the centre of the
aforementioned background; as Figure 1-c pointed
out, in the third scene (in D1), the white spot moves
with its position controlled by preset signals; and as
Figure 1-d exhibits, in the last scene (in D2), the
motion of the white spot follows the changes of CoP
of each subject, and a stationary blue circle is addi-
tionally displayed in the centre of the background.
Black
Black
Black
Black
da b c
Figure 1: Schematic representation of static and dynamic
visual scenes.
2.1 Subjects
Twenty-one healthy adult volunteers (seven females
and fourteen males) aging from twenty-two to thirty-
two years (mean ± standard deviation: age 25.7 ± 1.6
years; weight 61.4 ± 7.9 kg; height 169.1 ± 5.5 cm)
were included in this study. Every subject partici-
pated in all 40 trials of the four visual conditions.
None of the subjects had evidence or known history
of any gait, postural, or musculoskeletal disorder.
All of the subjects had normal or corrected-to-
normal vision. Informed consents were obtained
from all subjects prior to their participations.
2.2 Apparatus
The experiment was conducted in a closed area
(2.5m×4.0m) that was isolated with a shade curtain
and two walls, as shown in Figure 2.
Projector
2.5m
Force platform
4m
3m
Projection screen
2.2m
Wall
2m
Shade curtain
Figure 2: Schematic experimental environment.
In the closed area, a projection screen (1.5m
×2m) was hung on the front wall, a projector (To-
shiba TDP-T355) was fixed on the ceiling, and a
force platform (Kistler 9286BA) was settled hori-
zontally 2.2m from the projection screen. Connected
with the projector and the force platform, a desk-top
computer generated visual scenes, controlled the
CoP data acquisition, and performed other necessary
work, for example, data saving and processing.
2.3 Procedure
Subjects were instructed to stand barefoot on the
force platform in a comfortable stance, in front of
the projection screen, with their arms hanging natu-
rally beside their body.
In S1 and S2, subjects were required to keep
their body as immovable as possible, with their eyes
looking straight at the black background (for S1) or
focusing on the stationary white spot (for S2).
For D1, the spot rested at the centre of the back-
ground in the first five seconds, and moved with
preset signals during the left time of a trial. In verti-
cal direction, the preset signal was the summation of
a sinusoidal curve and a white noise, but in the hori-
zontal, just a white noise. In D1, subjects were asked
to keep their body as still as possible, with their eyes
fixed on the spot whether it held still or moved.
In the first five seconds of D2, the spot was lo-
cated at the centre of the background. In this stage,
subjects were asked to keep their body immovable
as much as possible, with their eyes focused on the
spot. At the end of this stage, the mean position
CoP
mean
of CoP was calculated, and the spot began
to move. During the left time of D2, the spot was
controlled by CoP of subjects and the displacement
of the spot was linear to the difference between the
current CoP and CoP
mean
. In coordinates, motions of
the spot from top to bottom and from left to right on
the background respectively denoted movements of
the CoP in anterior-posterior and media-lateral di-
rection. In this stage, subjects were instructed to
control their upright posture to make the spot to be
overlapped by the stationary circle, but relative
movements between the body components were not
allowed except between the feet and the else body
parts.
Several practice runs were performed prior to the
test to ensure that subjects had mastered the relation-
ship between the spot motion and their body sway,
and could act as the instructions asked them to do.
In our research, subjects needed to finish ten
40s-lasting trials for each condition. Between every
two of these ten repeated trials, subjects had one
minute of rest time, and after all of these ten trials, at
least ten minutes. Although only the data of the last
30s were valid in the signal processing, CoP data
were recorded all through every trial, with a 1 KHz
sampling frequency.
CHAOS LEVEL INVESTIGATION OF CENTRE-OF-PRESSURE SINGLE-STEP DISPLACEMENT IN STATIC AND
DYNAMIC VISUAL CONDITIONS
263

2.4 Signal Processing
According to Shannon entropy theory, the entropy of
a random variable is related to the information that
the observation of the variable gives. The more un-
predictable and unstructured the variable is, the lar-
ger its entropy (Hyvarinen, Karhunen, & Oja, 2001).
In our investigation, the CoP single-step displace-
ment is regarded as a random variable. Entropy of
this variable reflects the adjustment effects of the
postural control system. The larger the entropy is,
the less the variable is controlled.
Defined by Shannon entropy theory, the entropy
E of a random variable Y with probability mass func-
tion p
Y
(y
k
) is:
() () ()
∑
+∞
−∞=
−=
k
kYkY
ypypYE log
(1)
To get the entropy, the probability mass function of
CoP single-step displacements needs to be estimated.
Postulate the modulus R and the deflection angle Θ
of CoP single-step displacements are random vari-
ables. Their observations, r
k
>0 and θ
k
∈[0, π), are
calculated from CoP trajectories as demonstrated in
Figure 3 by the following equations:
()( )
2
1
2
1 −−
−+−=
kkkkk
yyxxr
(2)
1
1
arccos
−
−
⋅
⋅
=
kk
kk
k
rr
rr



θ
(3)
where
()( )
2111 −−−−
−−=⋅
kkkkkk
xxxxrr

()( )
211 −−−
−−+
kkkk
yyyy
(4)
()()
2
1
2
1 −−
−+−=
kkkkk
yyxxr

(5)
()( )
2
21
2
211 −−−−−
−+−=
kkkkk
yyxxr

(6)
(x
k,
y
k
)
(x
k-1,
y
k-1
)
(x
k-2,
y
k-2
)
θ
k
r
k
r
k-1
r
k+1
θ
k+1
(x
k+1,
y
k+1
)
Figure 3: Schematic representation of calculation of
r
k
and
θ
k
. (x
k-2
, y
k-2
), (x
k-1
, y
k-1
) , (x
k
, y
k
) and (x
k+1
, y
k+1
) are sequen-
tial points on a CoP trajectory.
Then, the finite value ranges [min(r
k
), max(r
k
)]
and [min(θ
k
), max(θ
k
)] of r
k
and θ
k
are divided into n
equal-lengthed subintervals individually:
() () []
∪
1
0
max,min
−
=
=
n
i
ikk
Rrr
(7)
() ()
[]
∪
1
0
max,min
−
=
Θ=
n
j
jkk
θθ
(8)
where ∀p, q∈[0, n-1], p≠q, R
p
∩R
q
=∅, and Θ
p
∩Θ
q
=∅.
Suppose m(
•) represent Lebesgue measure in R
1
. The
following equations are satisfied:
m
(R
0
)=m(R
1
)=…=m(R
n-1
) (9)
m
(Θ
0
)=m(Θ
1
)=…=m(Θ
n-1
) (10)
Let f
R
(i) and f
Θ
(j) respectively represent the ra-
tios of the numbers of r
k
and θ
k
in arbitrary subinter-
vals i and j and the total numbers of r
k
and θ
k
. The
estimation of the probability mass functions f
R
(r
k
)
and f
Θ
(θ
k
) of R and Θ can be obtained as follows:
() ()
()
()
}{
}:{
ˆ
k
ikk
RkR
r
Rrr
ifrf
μ
μ
∈
==
(11)
() ()
(
)
()
}{
}:{
ˆ
k
jkk
k
jff
θμ
θθμ
θ
Θ∈
==
ΘΘ
(12)
where i, j∈[0, n-1] and μ(
•) denoting the amount of
the elements in the set. Thus, the entropy of R and of
Θ are obtained by the following expressions:
()
)(log)(
10
1
0
ififRE
R
n
i
R
∑
−
=
−=
(13)
() )(log)(
10
1
0
jfjfE
n
j
Θ
−
=
Θ
∑
−=Θ
(14)
3 RESULTS
In a total of 840 trials in our investigation, for all
subjects and all visual conditions, the resultant en-
tropy of R of CoP single-step displacement remains
larger than entropy of Θ, without exception. Figure 4
demonstrates an example of our experiment results
for an individual subject, and Table 1 shows the en-
tropy results for the whole population of subjects in
different visual conditions.
Figure 4 and Table 1 explicitly indicate a regula-
tion that the entropy of R is always larger than en-
tropy of Θ, no matter in which visual environment.
This regulation reveals that the chaos level of CoP
single-step displacement is higher in amplitude than
in angular. Since CoP trajectories reflect perform-
ance of postural control, speculation can be deduced
from this result that human upright posture may be
regulated more in direction control than in amplitude
control under the four specific visual conditions.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
264

0 2 4 6 8 10
3
3.5
4
b
Entropy (Hart)
a
0 2 4 6 8 10
2.5
3
3.5
4
c
Entropy (Hart)
0 2 4 6 8 10
2.5
3
3.5
4
d
Entropy (Hart)
0 2 4 6 8 10
3
3.5
4
Experiment Number
Entropy (Hart)
Entropy
R
Entropy
θ
Figure 4: Entropy of
R and Θ of ten trials from one subject
in both the static and dynamic visual conditions: a. for S1;
b. for S2; c. for D1; d. for D2.
Table 1: General entropy of
R and Θ from the population
of subjects under different visual conditions.
Entropy of R (Hart)
(mean±SD)
Entropy of Θ (Hart)
(mean±SD)
S1 3.5808±0.0215 3.2421±0.0171
S2 3.6156±0.0196 3.2869±0.0173
D1 3.3803±0.0153 3.1407±0.0149
D2 3.3988±0.0135 3.1561±0.0143
4 DISCUSSION
In this study, the entropy of CoP single-step dis-
placement in human upright postural control under
specific visual conditions is investigated. This inves-
tigation presents a result of larger amplitude entropy
and smaller angular entropy of CoP single-step dis-
placement. This result suggests that the angular con-
trol is more regulated than the amplitude control in
human upright stance maintenance.
However, these findings may be related to our
experimental settings, for example, the visual scenes
provided. In our future research, alternation of visual
scenes will be made to further confirm our sugges-
tion that upright stance is more regulated in direction
control than in amplitude control. If this suggestion
can be confirmed, displaying more detectable visual
information will provide a feasible way to improve
the control ability of human upright stance. To this
extent, the chaos level investigation of CoP single-
step displacement through entropy analysis in this
presentation has directive significance for postural
experiment design and meaningful implications to
postural control improvement.
ACKNOWLEDGEMENTS
The author specially appreciates Professor John
Paddison for revising the English text. This research
was supported by National Nature Science Founda-
tion of China through the grant #60705021.
REFERENCES
Bronstein, A. M., 1986. Suppression of visually evoked
postural responses. In
Experimental Brain Research.
655-658.
Collins, J. J., & De Luca, C. J., 1993. Open-loop and
closed-loop control of posture: A random-walk analy-
sis of centre-of-pressure trajectories. In
Experimental
Brain Research
. 308-318.
Hidenori, K., & Jiang, Y., 2006. A PID model of human
balance keeping. In
IEEE Control Systems Magazine.
18-23.
Hyvarinen, A., Karhunen, J., & Oja, E., 2001.
Independent
Component Analysis
, John Wiley & Sons, Inc. New
York.
Mergner, T., Schweigart, G., Maurer, C., & Blümle, A.,
2005. Human postural responses to motion of real and
virtual visual environments under different support
base conditions. In
Experimental Brain Research. 535-
556.
Peterka, R. J., 2000. Postural control model interpretation
of stabilogram diffusion analysis. In
Biological Cy-
bernetics
. 335-343.
Rougier, P., 1999. Influence of visual feedback on succes-
sive control mechanisms in upright quiet stance in
humans assessed by fractional Brownian motion mod-
elling. In
Neuroscience Letters. 157-160.
Rougier, P., 2004. Optimising the visual feedback tech-
nique for improving upright stance maintenance by de-
laying its display: behavioural effects on healthy
adults. In
Gait and Posture. 154-163.
CHAOS LEVEL INVESTIGATION OF CENTRE-OF-PRESSURE SINGLE-STEP DISPLACEMENT IN STATIC AND
DYNAMIC VISUAL CONDITIONS
265