BIOSONAR-INSPIRED SOURCE LOCALIZATION IN LOW SNR
Sasha Apartsin
1
, Leon N. Cooper
2
and Nathan Intrator
1
1
Blavatnik School of Computer Science, Tel-Aviv University, Tel-Aviv, Israel
2
Institute For Brain and Neural Systems and Physics Department, Brown Univeristy, Providence, U.S.A.
Keywords: Biosonar, Underground exploration, Threshold effect, Source localization, Time of arrival.
Abstract: Some mammals use sound signals for communications and navigation in the air (bats) or underwater
(dolphins). Recent biological discovery shows that blind mole rat is capable of detecting and avoiding
underground obstacles using reflection from seismic signals. Such a remarkable capacity relies on the ability
to localize the source of the reflection with high accuracy and in very low Signal to Noise Ratio (SNR)
conditions. The standard methods for source localization are usually based on Time of Arrival (ToA)
estimation obtained by the correlation of received signal with a matched filter. This approach suffers from
rapid deterioration in the accuracy as SNR level falls below certain threshold value: the phenomenon known
in the Radar Theory as a “threshold effect”. In this paper we describe biosonar-inspired method for ToA
estimation and 2D source localization based on the fusion of the measurements from biased estimators
which are obtained using a family of unmatched filters. Suboptimal but not perfectly correlated estimators
are combined together to produce a robust estimator for ToA and 2D source position which outperforms
standard matched filter-based estimator in high noise. The proposed method can be applied for mapping of
underground instalments using low power infrasound pulses.
1 INTRODUCTION
Echolocation, also called Biosonar, is the biological
sonar used by several mammals such as bats,
dolphins and whales. Echolocating animals emit
calls out to the environment, and listen to the echoes
of those calls that return from various objects in the
environment. They use these echoes to locate, range,
and identify the objects. Echolocation is used for
navigation and for foraging (or hunting) in various
environments.
It has been recently discovered (Kimchi et al.,
2005) that the blind mole rat uses sonar-like
exploration of the underground. This rat, which lives
underground and has no functioning eyes, generates
ground stimulation by banging its head on the wall
of its tunnels.
Mole rat can dig a tunnel 300ft long in one night
while detecting and avoiding voids and obstacles
(e.g. stones) that are several feet ahead.
The tunnels of mole rats can reach a length of
two miles and a mole rat runs inside the tunnel at a
thus indicating that it can “see” quite well, although
This work was supported in part by the U.S. Army Research
Office
its eyes are not functioning. From behavioural
studies, we learn that a mole rat finds out if some
intruder got into its tunnel very quickly (as they
become very aggressive).
It thus follows; that the mole rat can utilize its
infrasound exploration device to a long range of
over a mile. How are the ping returns being
transformed into an image, we do not quite know,
but one can expect that the mechanism is similar to
the one employed by Bats, Dolphins and other
biosonar animal. However, in the case of blind mole
rat, the transmitted seismic pulse has low central
frequency or otherwise it will be quickly absorbed
by the soil.
Analysis of signals from returned pings is used
extensively in seismic underground exploration. The
method requires a controlled seismic source of
energy, such as dynamite, a specialized air gun or
vibrators, commonly known by their trademark
name Vibroseis. These seismic sources produce high
energy pulses to ensure high Signal to Noise Ratio at
receivers. Obviously, the energy of the explosion is
nowhere comparable to the power of pulses
generated by blind mole rat.
399
Apartsin S., Cooper L. and Intrator N..
BIOSONAR-INSPIRED SOURCE LOCALIZATION IN LOW SNR.
DOI: 10.5220/0003126803990404
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 399-404
ISBN: 978-989-8425-35-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

The typical analysis of returned signal involves
correlation of the returned signal with a matched
filter. The matched filter approach suffers from
rapid deterioration in the sensing accuracy as SNR
level falls below certain threshold value; the
phenomenon known in the Radar Theory as a
“threshold effect”(Woodward, 1953).
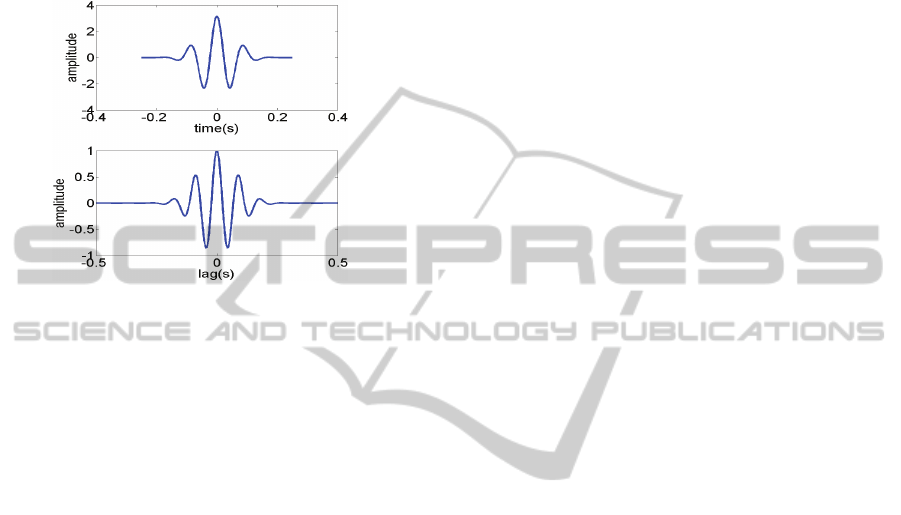
Figure 1: Gaussian modulated sinusoidal pulse (top) and
its autocorrelation function y(t).
According to Woodward who studied the
threshold effect back in 1953, it is “one of the most
interesting features of radar theory”. It appears that
when SNR at a receiver falls below certain threshold
value, the mean square error of the estimation
rapidly increases, causing dramatic drop in sensing
accuracy. A receiver operating with SNR above this
threshold value is said to be in a coherent state. The
matched filter-based estimator is usually used for the
coherent receiver. For the SNR levels substantially
below the threshold value, a receiver said to be
noncoherent with the assumption that most of the
information about the pulse carrier phase is lost due
to the noise. For in-between levels of SNR, a
receiver is said to be a semi-coherent receiver,
balancing between coherent and noncoherent states.
The threshold effect is intensified (i.e. occurs at
higher SNR levels) as pulse central frequency is
reduced. Therefore the conventional matched filter
approach might not be the best choice for the
processing of responses from low-power low-
frequency pulses.
In this paper, we describe a robust single pulse
ToA estimation method for semi-coherent receiver.
We show how to construct a family of suboptimal
and biased estimators, using phase-shifted versions
of source waveform as unmatched filters. The
outcomes of estimators are fused together into a
single ToA estimator, which outperforms
conventional Matched Filter (MF) based estimator
for a range of low SNR levels.
The same idea can be applied to the problem of
2D source localization, provided matched features
have complex reflection cross-section. In 2D case, a
family of unmatched filters can be generated from
the feature’s template using phase shift in several
directions. The increased number of degrees of
freedom (phase shift directions) results in even
larger improvement in the accuracy.
One of the possible applications for the described
method involves detection and mapping of the
underground installments by low-power infrasound
pulses. Using a family of unmatched filters, the
accuracy of the localization can be significantly
improved without increasing the power of source
pulses. Limiting pulse power has great importance
when exploration is performed by autonomous
robots (Morris et al., 2006) with limited energy
source or usage of higher energy pulses is not
desirable (e.g. in order to stay undetected in hostile
environment).
2 MAXIMUM LIKELIHOOD
MATCHED FILTER
ESTIMATOR
In remote sensing applications such as radar or
sonar, the common scenario starts by a transmitter
sending out a pulse waveform 
(

)
. The pulse is
reflected from a target and it is picked up by a
receiver at time 

. The estimated two-way travel
time (lag) can be used to calculate distance to the
target assuming the speed of the pulse propagation
in the medium is known.
The signal recorded at the receiver might be
represented as

(

)
=∗
(
−

)
+()
where 
(

)
is Additive White Gaussian Noise
(AWGN) which corrupts the signal. The  < 1
factor is used to account for all non-free space
propagation losses (e.g. attenuation of the signal in
the medium). We are interested in estimating the
Time of Arrival (ToA) parameter 

under the
assumption that noise  is large relative to c*s(t).
The standard method for ToA estimation
employs Matched Filter (MF) applied to the received
signal. The Matched Filter maximizes peak signal to
mean noise ratio (Whalen, 1995), making its output
suitable for the Maximum Likelihood (ML)
estimator of the ToA. The Matched Filter Maximum
Likelihood (MFML) estimator of ToA is obtained by
taking the position of the global maximum in the
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
400

output of the Matched Filter (MF). The output of the
Matched Filter can be expressed as a correlation of
the signal with the pulse waveform:

(

)
=
(

)
∘
(

)
=
(

)
+()
Where 
(

)
is scaled and shifted version of the
pulse’s autocorrelation function and 
(

)
is filtered
noise. A typical Gaussian-modulated sinusoidal
pulse and its autocorrelation function are shown in
Figure 1.
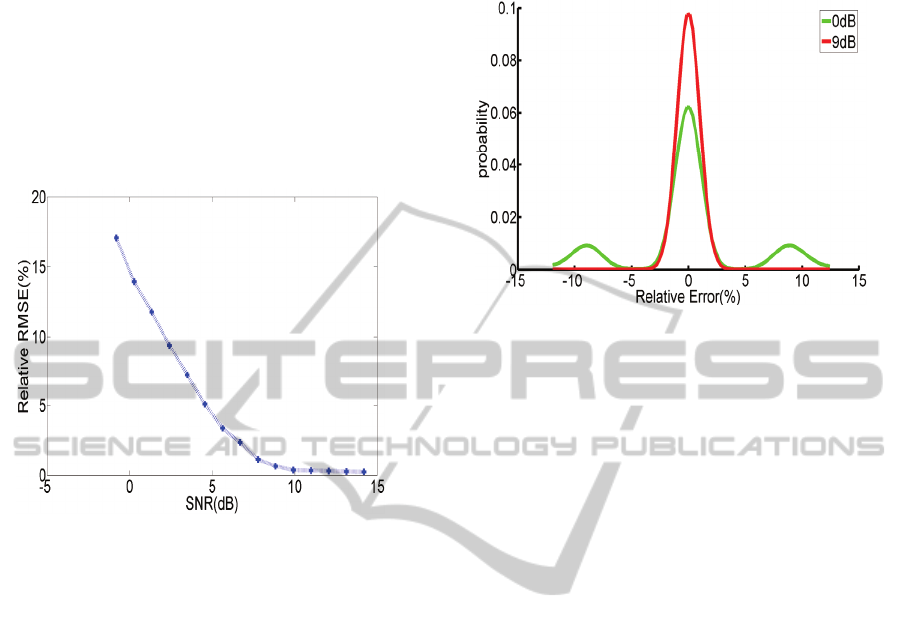
Figure 2: The MFML estimator threshold effect. The error
increases rapidly as SNR falls below a threshold.
In the absence of noise, the maximum value of

(

)
is achieved at  = 

. As the level of noise
increases, the filtered noise 
(

)
may cause a slight
shift in the location of the peak of 
(

)
. However, at
the high noise levels, a location around one of the
side lobes of 
(

)
may occasionally become the
global maximum of 
(

)
.
A side lobe of autocorrelation function
mistakenly taken as its global maximum is a major
reason behind deterioration in accuracy of MFML
estimator known as threshold effect (Woodward,
1953). The threshold effect manifests itself in rapid
increase in the Root Mean Square Error (RMSE) of
the MFML estimator as shown in the Figure 2. In
semi-coherent state, the posterior distribution of the
possible lag locations becomes multimodal (Figure
3) because of the significant height of
autocorrelation function’s side lobes.
The height of the side lobes of the
autocorrelation function is affected by the pulse
bandwidth. Therefore, the threshold effect is
considerable for low-frequency narrowband pulses.
The analysis of the performance of different time-of-
arrival estimation methods is essential for Radar,
Sonar and other remote sensing applications. Rather
than compute the exact error of a specific estimator,
it is often more convenient to lower-bound the error
of any estimators for a given problem.
Figure 3: The probability density function for MFML
estimator error. There are significant local maxima under
low SNR.
The conventional Matched Filter Maximum
Likelihood (MFML) estimator is considered
efficient as it asymptotically attains the Cramer-Rao
Bound (CRB) under sufficiently high SNR
conditions (Van Treese,
1968). However, under
lower SNR levels, the Cramer-Rao Bound appears to
be over-optimistic and a more tight forms of bound
are required if the level of noise is high. The
Barankin Bound (Barankin, 1949) and associated
Barankin Theory provide tools for constructing
useful bounds for mean error of an estimator under
low SNR. Although in its general form the Barankin
bound depends on the estimated parameter and
therefore can’t be easily computed, it is able to
account for the threshold phenomena in the
estimation of the time-of-arrival parameter.
3 UNMATCHED FILTER
MAXIMUM LIKELIHOOD
ESTIMATOR
Given an arbitrary pulse waveform
(

)
, we
construct a pair of Phase Shifted Unmatched (PSU)
filters 


(

)
and 


(

)
by shifting the phase of
each pulse by + and − respectively. A
Gaussian-modulated sinusoidal pulse and its PSU
filter pair generated using =/ are shown in
Figure 4.
The cross correlation of the signal 
(

)
and a
PSU pair’s filter can be expressed as:


±
(

)
=
(

)
∘

±
(

)
=

±
(

)
+

±
(

)
BIOSONAR-INSPIRED SOURCE LOCALIZATION IN LOW SNR
401

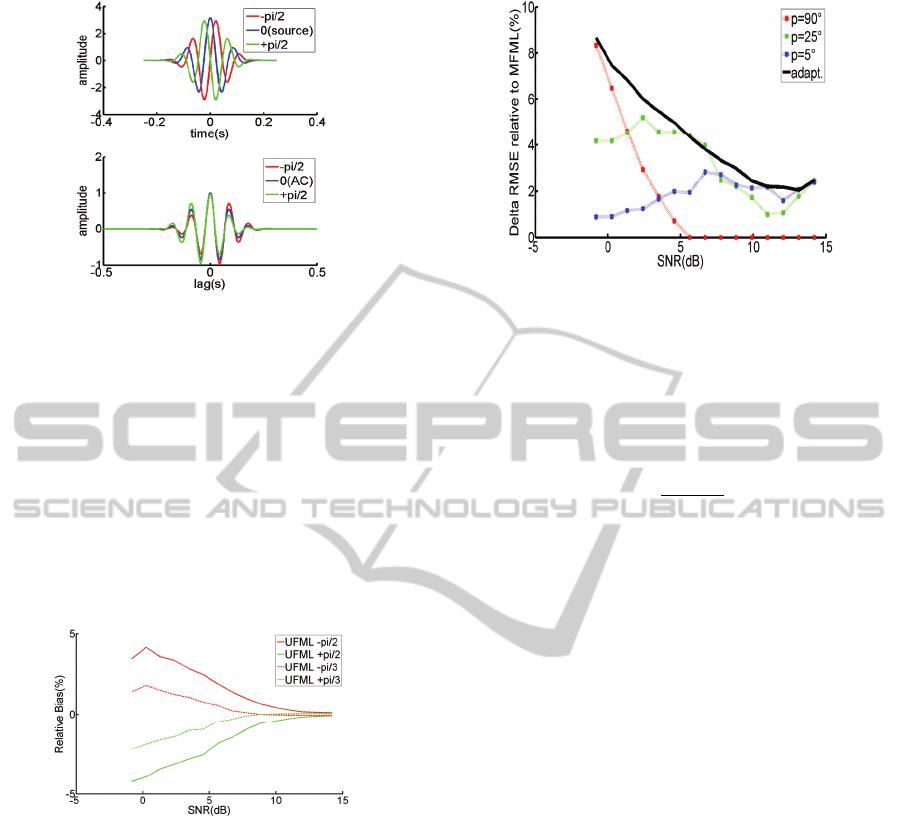
Figure 4: Phase shifted pulses (top) and their cross
correlation functions (bottom). Note asymmetric shape of
side lobes.
The Unmatched Filter Maximum Likelihood
(UFML) estimators 


and 


corresponding to a
PSU pair can be defined as:


±
=

±
(

)
 = (
(

)
∘

±
(

)
)
The side lobes of the cross-correlation function


±
(

)
=
(

)
∘

±
(

)
have unequal heights, making
the UFML estimators biased toward the higher side
lobe as shown in Figure 5.
Figure 5: Bias of UFML estimator pair. Unmatched filter
pair produces biased estimator pair with bias of the same
value but opposite sign.
The bias of the two UFML estimators has equal
absolute value but opposite sign due to symmetry in
the heights and position of the cross-correlation side
lobes. As SNR is increased, the bias decreases since
the position of the cross-correlation maximum is less
affected by the noise. Note that autocorrelation and
PSU filter cross-correlation produce signals of the
same power, however application of unmatched
filter produces lower peak signal-to-mean-noise ratio
as compared to matched filter.
The Root Mean Square Error (RMSE) of a single
UFML estimator is higher as compared to the RMSE
of MFML. However, the UFML estimators
corresponding to a PSU filter pair are not perfectly
correlated.
Figure 6: RMSE improvement by fixed and adaptive phase
AoUFML estimators. For each SNR there is the best
performing value of a phase shift (color lines). The black
line shows error for adaptive selection of phase-shift
value.
Therefore we can define a new estimator by
averaging results from a pair of UFML:


=



+



At low SNR levels, the resulting Average of UFML
(AoUFML) estimator has lower RMSE as compared
to MFML (Figure 6).
The AoUFML estimator outperforms MFML
estimator at SNR levels corresponding to semi-
coherent receiver state. At higher SNR levels, the
effect of side lobes is insignificant, therefore, the
shape of the main peak of cross-correlation function
have critical impact on the estimator’s RMSE. Since
an unmatched filter produces smaller peak signal-to-
mean-noise ratio and the UFML pair is almost
perfectly correlated at higher SNR levels, the MFML
estimator outperform the AoUFML estimator 

at
coherent receiver state.
The crossover points between AoUFML and
MFML RMSE curves can be controlled by choosing
appropriate phase shift parameter  as described in
(Apartsin et al., 2010). Finally, we note that many of
the commonly used source waveforms have side
lobes in their autocorrelation function (e.g. Ryan,
1994). Therefore, although the effectiveness of the
proposed method is demonstrated using Gaussian-
modulated sinusoidal pulse, the method can be
applied to other source waveforms as well.
4 2D SOURCE LOCALIZATION
The described method can be used for the
localization of reflection source in 2D or 3D
seismic/acoustic maps. Using sensor arrays, a 2D or
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
402

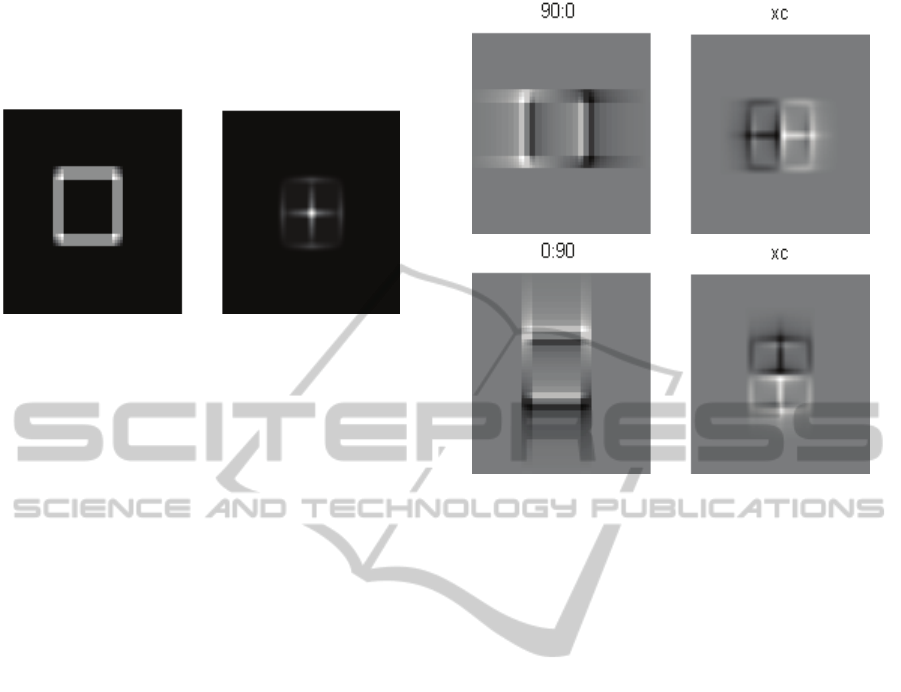
3D image of the underground can be computed. On
the computed map we might want to pinpoint the
location of specific features and voids like a “box”
feature shown at Figure 7(left).
Figure 7: Left: Density map of a “box” feature (void),
Right: 2D autocorrelation function, lighter points
corresponds to larger values. There are 4 local peaks in
autocorrelation function corresponding to 4 edges of the
box.
If underground exploration is performed using
low power low frequency seismic pulses, the
resulting image would be heavily corrupted by noise.
As in one-dimensional case, the estimation of a
feature position using conventional matched filters
or 2D template would suffer from the threshold
effect due to existence of 4 local peaks in the
feature’s 2D autocorrelation function (Figure 7
right). Again, instead of relying on a correlation with
a single matched filter, the family of 2D unmatched
filters using a phase shift can be generated.
Unlike the one-dimensional case, in 2D we have
greater choice of phase directions. It seems
reasonable to choose phase shift values in the
direction of local peaks of the autocorrelation
functions. For “box” feature it translates into the
vertical and horizontal directions of phase shift. This
choice of directions corresponds to the family of 4
unmatched filters (two members of this family are
shown at Figure 8). Estimators corresponding to
each unmatched filter are biased toward one of the
two local maxima in the direction of the phase shift.
However, the estimators are not completely
correlated as in one dimensional case.
Therefore, by averaging the position of the peaks
obtained by cross-correlating noisy map image with
filters from the constructed filter family, the
accuracy of the position estimation (localization) of
the feature is significantly improved (Figure 9). For
features with more complex configuration the
number of filters can be increased even further to
account for all of local maxima in autocorrelation
function.
Figure 8: Phase-shifted 2D filters (left column) and their
cross-correlation with “box” feature (right column) for
horizontal (top row) and vertical (bottom) phase shift
directions.
5 CONCLUSIONS
Inspired by the capability of blind mole rat to cope
with the threshold effect while exploring
underground using low-power low-frequency pulses,
we suggest a method for robust time of arrival
estimation and 2D source localization and template
matching.
We showed that using Phase Shifted Unmatched
(PSU) filters, a pair of Unmatched Filter Maximum
Likelihood (UFML) estimators can be computed to
obtain biased Time of Arrival estimators. In semi-
coherent receiver state, the UFML estimators are not
perfectly correlated and, therefore, can be combined
together into estimator that outperforms
conventional Matched Filter Maximum Likelihood
estimator.
The described method can be applied for 2D
source localization using a family of Unmatched
Filters generated by phase shifting original template
in multiple directions. The method can be applied
for underground exploration and mapping using low
power low frequency seismic signals.
BIOSONAR-INSPIRED SOURCE LOCALIZATION IN LOW SNR
403

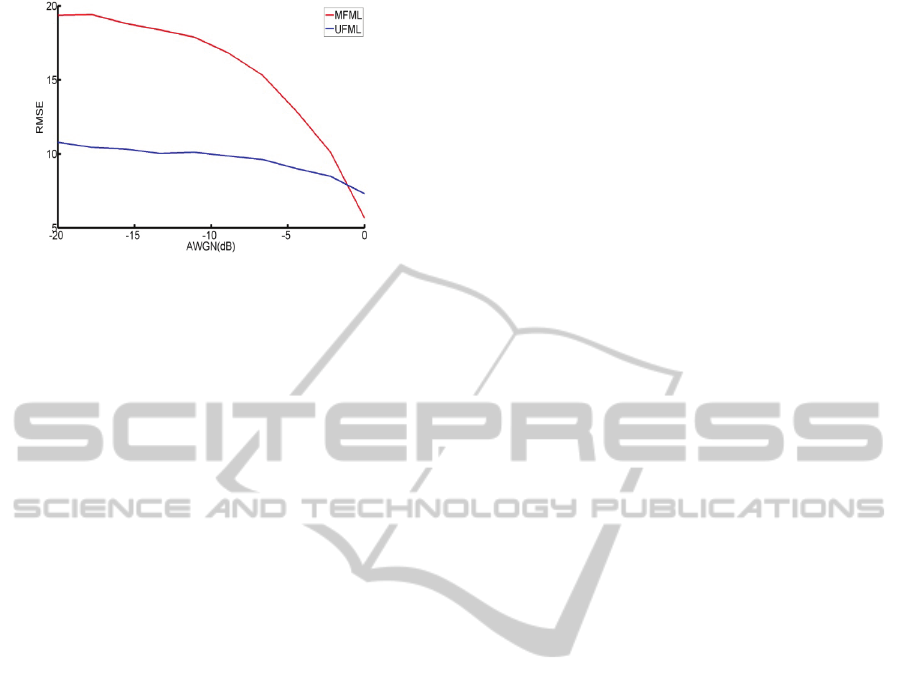
Figure 9: RMSE as function of SNR Using fusing from 4
estimators (2 horizontal phase shift and 2 vertical phase
shift) gives higher accuracy than conventional matched-
filter approach.
REFERENCES
Apartsin, S. Cooper, L. N. and Intrator, N., 2010. SNR-
Dependent Filtering for Time of Arrival Estimation in
High Noise. To appear in Proc. IEEE Int. Workshop
on Machine Learning for Signal Processing (MLSP).
Barankin, E. W., 1949. Locally best unbiased estimates.
Ann Math. Statist., 20, pp477-501.
Kay, S. M., 1993. Fundamental of Statistical Signal
Processing. Prentice Hall.
Kimchi, T., Reshef, M. and Terkel, J., 2005. Evidence for
the use of reflected self-generated seismic waves for
spatial orientation in a blind subterranean mammal.
Journal of Experimental Biology, vol208, pp647-658.
Liao, H. S. and Gan, L. and Wei, P., 2009. A blind SNR
estimation method for radar signal. , IET international
RADAR conference.
McDonough, R. N., Whalen, A. D., 1995. Detection of
Signals in Noise. Academic Press.
Morris, A. and Ferguson, D. and Omohundro, Z., Bradley,
D., Silver, D., Baker, C., Thayer, S., Whittaker, C. and
Whittaker, W., 2006. Recent developments in
subterranean robotics. Journal of Field Robotics,
23(1), 35-57.
Pauluzzi, D. R., Beaulieu N. C., 2000. A comparison of
SNR estimation techniques for the AWGN channel.
IEEE Transaction on Communications. Volume 48,
Issue 10, pp1681-1691.
Ryan, H., 1994. Ricker, Ormsby, Klauder, Butterworth-A
choice of wavelet. CSEG Recorder, Vol. 19-7.
Sadler, B. M., Kozick, R. J., 2006. A Survey of Time Delay
Estimation Performance Bounds. Fourth IEEE
Workshop on Sensor Array and Multichannel
Processing, pp.282-288.
Skolnik, M. I., 1962. Introduction to Radar Systems.
McGraw-Hill.
Succi, G. P., Prado, G., Gampert, R. and Pedersen, T. K.,
2000. Problems in Seismic detection and Tracking.
Proceedings of SPIE, vol. 4040, pp165-173.
Woodward, P., 1953. Probability and Information Theory,
with Applications to Radar. McGraw-Hill.
Van Treese, H. L., 1968. Detection, Estimation and
Modulation Theory. John Wiley & Sons, Inc.
Varshney, L. R., Thomas, D., 2003. Sidelobe reduction for
matched filter range processing. Proceedings of IEEE
Radar Conference, pp446-451.
Yu, L., Neretti, N. and Intrator, N., 2006. Multiple ping
sonar accuracy improvement using robust motion
estimation and ping fusion. Journal of the Acoustic
Society of America. Volume 119, Issue 4, pp2106-
213.
Zeira A. and Schultheiss, P. M., 1994. Realizable lower
bounds for time delay estimation-Part II: Threshold
phenomena. IEEE Trans. Signal Processing,
Volume42, Issue 5, pp1001-1007.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
404