DESIGN OF A PRESSURE SENSOR FOR MONITORING OF

POST-ENDOVASCULAR ANEURYSM REPAIR

A. T. Sepúlveda, A. J. Pontes, J. C. Viana, L. A. Rocha

Institute for Polymers and Composites/I3N, University of Minho, Braga, Portugal

Isa C. T. Santos

Instituto de Engenharia Mecânica e Gestão Industrial / Faculdade de Engenharia, Universidade do Porto, Porto, Portugal

F. Fachin, R. Guzmán de Villoria, B. L. Wardle

Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA, U.S.A.

Keywords: Implantable pressure sensor, Aneurysms, Carbon nanotubes, Pressure sensor design.

Abstract: This paper introduces the design and fabrication process of a flexible pressure sensor for monitoring post-

endovascular aneurysm repairs (EVAR). Biocompatible flexible PDMS membranes with embedded aligned

carbon nanotubes (CNTs) with a conductivity of 11 S.m

-1

and elastic modulus of 2 MPa are used to build a

LC network for passive telemetry readout-out. The pressure sensor has a modelled sensitivity 14fF/mmHg

for a pressure range between 6-47 mmHg, in agreement with the required application. The pressure sensor,

with a 250 µm thickness and total area of 1 cm

, will be contained within the stent-graft and used to

measure the pressure inside the aneurysm sac to detect complications related to the EVAR procedure.

1 INTRODUCTION

An aneurysm can be defined as a permanent and

irreversible localized dilatation of an artery, having

at least a 50% increase in diameter compared with a

normal one. Aneurysms can appear anywhere but

they most commonly occur in the aorta, as well as in

arteries located at the base of the brain and in the

legs.

Two treatments are currently available for the

treatment of aneurysms: conventional surgical repair

(open surgery) (Myers, Devine, Barras and Self,

2001) and endovascular aneurysm repair (EVAR)

(Parodi, Palmaz, and Barone, 1991). The first

involves making a relatively large incision in the

abdomen and inserting a prosthetic graft to replace

the damaged section of the aorta. This procedure can

also be performed laparoscopically, either by hand-

assisted laparoscopic surgery or total laparoscopic

surgery. EVAR is a minimally invasive procedure in

which a stent-graft is guided from the femoral artery

to the affected artery segment in order to prevent

wall rupture, thereby shielding the aneurysm from

the blood pressure. This treatment is usually

associated with less physiological derangement,

lower morbidity and mortality, and more rapid

recovery than open surgery (Chuter, Parodi, and

Lawrence-Brown, 2004) but regular

monitoring/surveillance to detect and prevent

complications such as graft migration, stent fracture,

endoleaks, enlargement of the aneurysm sac, and

abdominal aortic aneurysm AAA rupture are

required (Katzen and MacLean, 2006) after the

procedure.

Comparing both approaches, EVAR is preferable

as it is less stressful, it significantly reduces

systemic complications (Rutherford and Krupski,

2004), and it has both lower costs associated with

inpatient stay and less (or no) need for intensive care

facilities during recovery (Myers et. al. 2001,

Hayter, Bradshaw, Allen, Guduguntla and Hardman,

2005). The durability of open surgery, established

with long-term follow-up studies, is excellent

(Rutherford and Krupski, 2004), so good that there

T. Sepúlveda A., J. Pontes A., C. Viana J., A. Rocha L., C. T. Santos I., Fachin F., Guzmán de Villoria R. and L. Wardle B..

DESIGN OF A PRESSURE SENSOR FOR MONITORING OF POST-ENDOVASCULAR ANEURYSM REPAIR.

DOI: 10.5220/0003127400140022

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 14-22

ISBN: 978-989-8425-37-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

is little or no requirement for long-term surveillance,

in contrast with EVAR whose current results suggest

that there is a need for increased surveillance and re-

intervention (Hayter et al., 2005, Michaels, Drury,

and Thomas, 2005, Greenhalgh, 2005). Considering

the longer life expectancies and the rising public

expectations for quality of life, the costs associated

with follow-up can jeopardize EVAR’s

effectiveness.

The current surveillance protocol involves

imaging at 1, 6, and 12 months after the procedure,

and thereafter, on an annual basis (Milner, Kasirajan

and Chaikof, 2006). In order to reduce and even

eliminate these exams, new surveillance

technologies are being investigated, with the most

promising technique identified thus far being

remote pressure sensing (Milner et al., 2006).

Remote pressure sensing enables the measurement

of both the systolic and diastolic pressures within the

residual aneurysm sac at any given point in time.

Thus far, the Impressure Sensor (Remon Medical

Technologies, Israel) and the CardioMems

EndoSure Wireless AAA Pressure Sensor

(CardioMems, Inc, USA) have been evaluated for

abdominal aortic aneurysms (AAA) (Milner et al.,

2006, Springer, Günther, and Schmitz-Rode, 2007).

This work introduces a new pressure sensor for

endotension measurement. The focus is on the use of

a flexible substrate enabling the conformability of

the sensor to the stent-graft and thus the aorta.

Compared to currently available devices, this aspect

brings several advantagessince the sensor can be

attached to the stent-graft and delivered in a single

procedure (as oposed to the requirement of two

catheters for the CardioMems device) and it enables

the placement of more than one sensor (a sensor

cluster) contributing to a more comprehensive study

of post-EVAR aneurysm evolution (that is currently

not possible).

The contributions in this paper are divided in 5

sections. After an introduction to the topic, the

required sensor specifications are derived followed

by the development of an electro-mechanical

pressure sensor model. Next, a new fabrication

process for the realization of the flexible sensor is

introduced and finally some experimental results and

conclusions are presented.

2 SENSOR SPECIFICATIONS

Research on implantable pressure sensors is very

active and has been supported and justified by the

need of continuous pressure monitoring for patients

with congestive heart failure, as an early diagnostic

mechanism for some risk patients and for post-

EVAR surveillance (Receveur, Lindemans, and de

Rooij, 2007, Potkay, 2008). Implantable pressure

sensors are typically categorized into extra-arterial

blood pressure and intra-arterial blood pressure

(Potkay, 2008) devices. Extra-arterial pressure

sensors are placed around the blood vessel and

perform an indirect pressure measurement through

the wall or through the expansion and contraction of

the artery, requiring however an invasive surgical

procedure for their implant while the intra-arterial

devices are in contact with the blood stream, inside

of the blood vessels.

Potkay (2008) defined a set of requirements for

pressure sensors according to the problem to be

addressed. In the case of EVAR, the requirements of

the pressure sensor are shown in Table 1.

Table 1: Requirements for post-EVAR surveillance

(Potkay, 2008).

Characteristic Value

Measurement location

Between graft and

aneurysm wall

Typical values (mmHg) 20 to 90

Measurement range (mmHg) 20 to 250

Measurement resolution (mmHg) 1

Measurement absolute accuracy

(mmHg)

Signal bandwidth (Hz) 0 to 80

Arterial diameter (mm) 15 to 40

After stent-graft placement, the aneurysm sac

gets depressurized and the pressure drops down to a

few mmHg. A numerical study performed by Li and

Kleinstreuer (2006) shows that after EVAR the

pressure inside the aneurysm sac is around 12% of

the current luminal pressure. Therefore, if one wants

to sense the luminal pressure value (which ranges

typically between 60 – 160 mmHg) through the

aneurysm sac pressure, the sensor must be able to

measure pressures between 6-16 mmHg with a

resolution of 0.1 mmHg. In addition, the sensor

needs a high dynamic range in order to detect stent-

graft complications (in this case the sac gets

pressurized and pressure increases to the luminal

pressure values).

2.1 Telemetry System

The pressure monitoring system under development

uses a passive telemetry system, based on an

DESIGN OF A PRESSURE SENSOR FOR MONITORING OF POST-ENDOVASCULAR ANEURYSM REPAIR

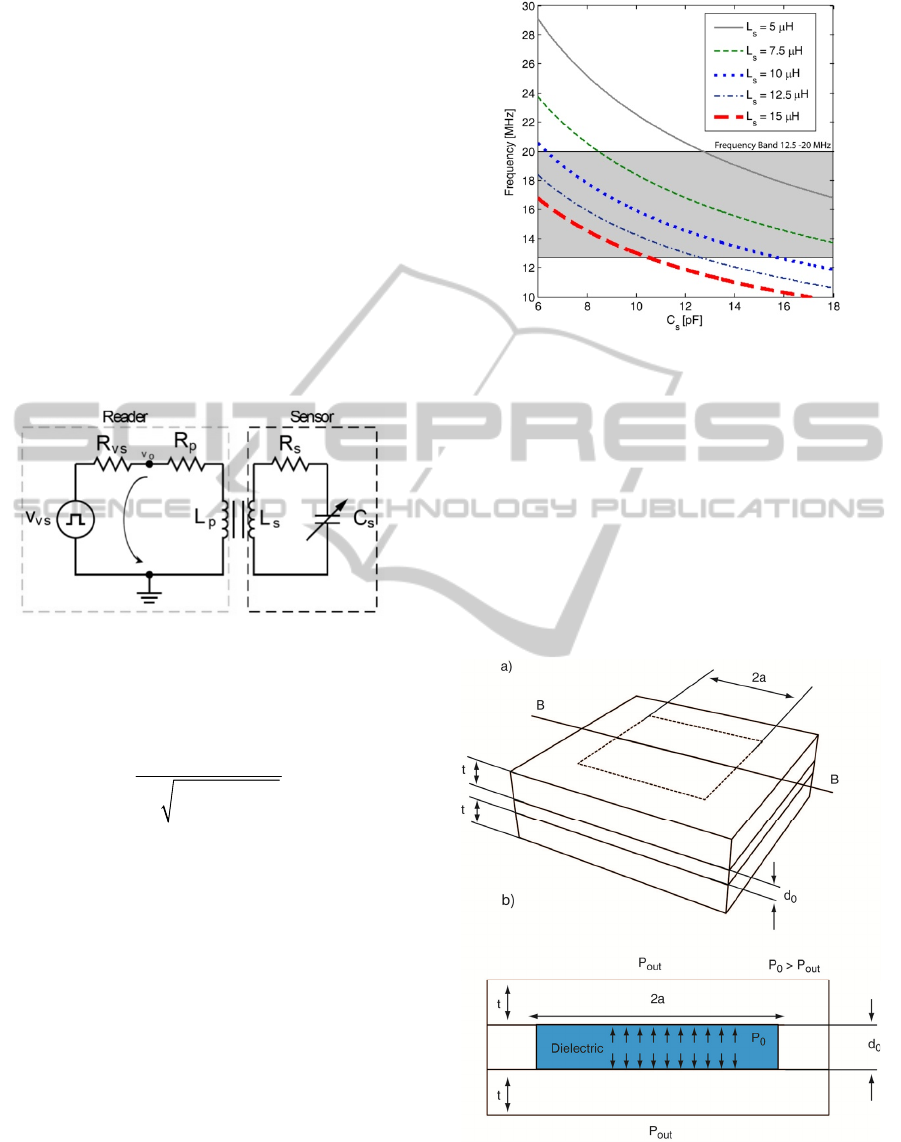
implantable LC resonant network, for the external

readout of the pressure sensor signal. The use of

passive telemetry in implantable medical devices is

well established (Mokwa, 2007) and enables the

realization of active implants with no power

constraints. A circuit representation of the sensor

system and external reader, using the transformer

model (parasitic capacitance is not included), is

presented in Figure 1. The components in the sensor

are modelled as passive elements: a variable

capacitor C

whose value changes with the applied

pressure, connected to an inductor L

, resulting in a

parallel resonant circuit. The schematic

representation in Figure 1 includes also the resistors

and R

which model the parasitic elements

associated with the inductors L

and L

and the

capacitor C

Figure 1: Telemetry circuit.

If the transformer is replaced by its T model, the

following expression for the oscillating frequency is

obtained:

()

osc

kLC

−

(1)

where k represents the coupling coefficient of the

transformer.

The system oscillation frequency was chosen to

operate in the frequency band from 12.5 to 20.0

MHz, allocated specifically for medical applications.

This frequency band presents additional advantages,

unlike low operational frequencies, since the

inductors and capacitors require small dimensions

and therefore small sensors’ area. Assuming a k =

0.06 (expected value for a distance of 5cm between

the sensor system and the external reader) Equation

1 is used to assess the capacitance and inductor

values required for the chosen frequency band. The

results are presented in Figure 2.

Figure 2: Telemetry system oscillating frequency vs.

capacitance for several inductor values.

A detailed analysis as that shown in Figure 2

reveals that for inductors ranging from 5 to 15 μH,

the capacitive changes should be between 5 and 18

pF to be within the chosen frequency band. The

external reader is expected to have a resolution

better than 1 kHz. If an inductor of 12.5 μH is used

during the design of the sensor, the capacitive

pressure sensor changes should be within the

interval 5-12 pF for pressure variations between 6 to

120 mmHg.

Figure 3: Schematic of the pressure square (sidelength =

2a) sensor a) 3D view and b) section cut B-B.

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

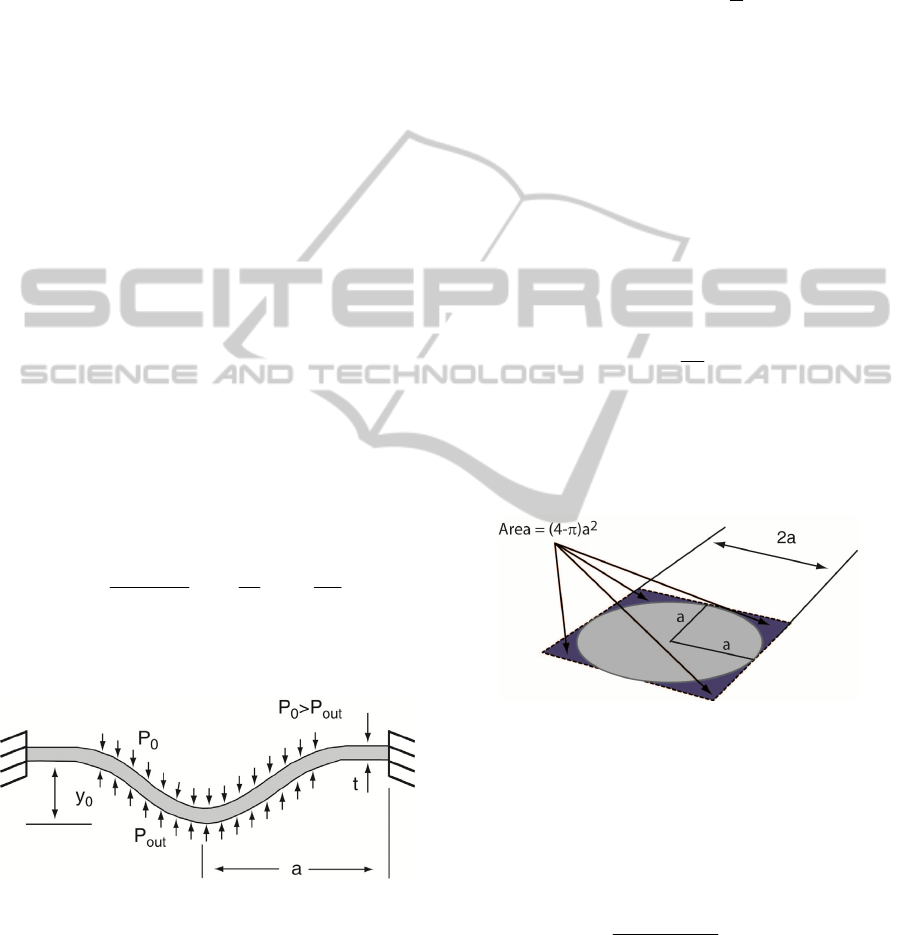
3 PRESSURE SENSOR MODEL

The proposed pressure sensor is based on two

square-plate (diaphragm) electrodes separated by a

dielectric (air, at a pressure P

). Changes on the

outside pressure (P

out

) deform the square plate and

consequently generate a capacitive change. A

schematic of the square platform (sidelenght of 2a)

pressure sensor is shown in Figure 3.

The sensor involves two coupled domains,

mechanical and electrical, that define the sensor

behaviour. An analysis of the behaviour of the two

domains leading to the final model is performed

next.

3.1 Mechanical Domain

The starting point to build the analytical model is the

generic square diaphragm described in Figure 4

where a is the sidelength, t is the thickness and y

the deflection. The diaphragm is clamped at the

edges.

For a clamped diaphragm under a uniform load

(like pressure), the angle of deflection, ϕ, can be

defined as equal to zero at the center (r = 0) and at

the edge (r = a) of the diaphragm. For these

boundary conditions, the deflection of a square

diaphragm under a pressure load can be modelled by

(Chau and Wise, 1987):

24 3

4.20 1.58

(1 )

out

⎡⎤

−= +

⎢⎥

−

⎣⎦

(2)

where

is the Poisson’s ratio, E is the Young’s

modulus, and

P=P

-P

out

is the pressure load.

Figure 4: Generic model for a deflectable diaphragm.

Equation (2) allows the calculation of the

deflection at the center of the diaphragm for a given

pressure load, but, the deflection along the

diaphragm is still required to model the capacitive

changes due to gap variation. The complexity of the

mechanical deflection model makes it difficult to

obtain a closed form solution for the deflection of

the diaphragm from the center to the edges.

Assuming large deflections (expected due to the

elasticity and low Young’s Modulus of the flexible

membranes) a circular deflection is considered and

introduced here as:

() sin arccos

yr y

⎛⎞

⎜⎟

⎝⎠

(3)

Although the profile given by equation (3) might

introduce some errors, it enables the calculation of a

closed form expression for the changes in the

capacitor.

3.2 Electrostatic Domain

A capacitor is an electronic component with two

electrodes that are separated by a dielectric. For the

simple case of a parallel plate capacitor, and in the

absence of displacements, the model for the

capacitor is:

εε

= ,

(4)

where

is the permittivity of free space

(

8.8546x10-12 F/m),

is the relative permittivity, w

and

l are the width and length of the capacitor

electrodes, and

is the gap between the electrodes.

Figure 5: Area of a circular diaphragm vs. square

diaphragm.

Since the capacitive sensor proposed here uses

diaphragm electrodes with a complex bending

profile, integration over the effective area of the

electrodes is required to compute the total

capacitance:

2(,)

Cdxdy

ddxy

εε

∫∫

(5)

where d(x,y) is the distance between electrodes due

to the diaphragm bending at position x, y. The

integration of the bending profile of a square

diaphragm is a complex exercise, and therefore, an

interesting solution is to consider a circular

diaphragm and use integration along the radius to

DESIGN OF A PRESSURE SENSOR FOR MONITORING OF POST-ENDOVASCULAR ANEURYSM REPAIR

compute the capacitance (see Figure 5). With this

simplification and replacing d(x,y) in equation (5)

for y(r) yields for the capacitor model:

()

(

)

00 00 0

2 sin arccos

ln( ln( 2 ) 2

Crdrd

ad d d y y

εε

⎛⎞

⎜⎟

⎝⎠

−++

∫∫

(6)

The total capacitance, considering the areas not

covered by the circular diaphragm, and assuming an

average bending at the corners of 8% of the total

bending is:

(4 )

0.08

total d r

εε

−

(7)

4 FABRICATION PROCESS

Given the characteristics of the application (the

sensor will be attached to the stent-graft) the

capacitive sensor must be foldable, extremely

flexible and characterized by a very small profile. In

addition, the technology should be simple and

biocompatible. Silicon based microtechnologies are

widely used in implantable medical devices

(Receveur et al., 2007), but due to the application

specifications, a new fabrication process is being

developed.

The proposed fabrication process uses aligned

carbon nanotubes (CNTs) to build the conductive

elements, namely the inductor and the capacitor

electrodes. The CNTs are embedded in a flexible

substrate of polydimethylsiloxane (PDMS), a

transparent, nontoxic and biocompatible silicone

elastomer.

The fabrication process flow for the development

of the flexible pressure sensor is schematically

presented in Figure 6. Acrylic moulds are produced

by CNC milling (Figure 6a) for posterior fabrication

of the PDMS membranes. This technique has low

costs and fast production times, but it is associated

with poor dimensional control (dimensions less than

50μm are difficult to achieve).

The electrical components (capacitor electrodes

and inductor) are based on aligned CNTs, as shown

in Figure 6b. Chemical vapour deposition (CVD) is

used to grow forests or “carpets” of vertically-

aligned CNTs (Bello, Hart, Ahn, Hallock,

Yamamoto, Garcia, Ellenbecker and Wardle, 2008).

Figure 6: Fabrication process flow for the development of

a flexible pressure sensor with aligned-CNT/PDMS

nanocomposites.

A silicon substrate with patterned Fe/Al

catalyst

is placed on a horizontal quartz tube furnace at

atmospheric pressure at 750 ºC (Hart, and Slocum,

2006) for the CNT growth. This method has the

advantage of allowing growth of high purity, high

yield and vertically aligned morphology. Next, the

CNTs are embedded into the polymer matrix

(PDMS). This step is schematically represented in

Figure 6c. The substrate is placed against the

moulds, and the PDMS is introduced in the cavities

through a hole, followed by the curing of the

elastomer.

The flexible pressure sensor is composed of three

thin layers, with the top and bottom layers defining

the inductor and the electrodes, and the middle one

defining the dielectric (air). This configuration

requires bonding of PDMS membranes. Eddings,

Johnson and Gale (2008) tested five different

bonding techniques and the highest reported bond

strength was obtained for both partial curing and

uncured PDMS adhesive techniques. The latter

approach has proven successful in our work as well,

and will be used for future experimentation.

5 RESULTS AND DISCUSSION

The key step of the fabrication process is the CNT-

PDMS impregnation and respective mechanical and

electrical properties (required for the sensor design).

Acrylic moulds have been fabricated (Figure 7), and

are being used to build the PDMS flexible

membranes with embedded CNTs (Figure 8).

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

Aligned CNTs are oriented in the out-of-plane (or

normal to the wafer plane) direction such that the

polymer nanocomposite can be presumed

transversely isotropic, i.e., isotropic in the plane of

the sensor. Furthermore, the modulus enhancement

due to CNTs is likely minimal as the long axis of the

CNTs are oriented perpendicular to the loading

direction, such that the PDMS polymer dominates

the response. Recent work has shown significant

increase in modulus due to aligned CNTs in polymer

(PDMS) (Ajayan et al., 2000) and epoxy (Cebeci et

al., 2009) in the CNT axis direction, but little

reinforcement effect in the transverse direction as

used here. This result is expected from composite

micromechanics analyses and experimental results.

Figure 7: Fabricated acrylic moulds for the production of

PDMS membranes.

Figure 8: PDMS membrane with embedded aligned CNTs

a) normal (the “z” axis corresponds to the direction of

CNTs) and b) folded.

5.1 Electrical and Mechanical

Characterization

Preliminary measurements of a series of PNC

samples (PDMS membranes with embedded CNTs)

indicate an electrical conductivity of 11.43 S.m

-1

with a standard deviation of 13.37 S.m

-1

. The

relatively high value of the standard deviation is

related to the manual process being used for the

membrane fabrication which gives origin to some

imperfections.

Some other samples where subject to mechanical

tests to obtain the elastic modulus and tensile

strength. The PDMS/CNTs specimens were

moulded into rectangular shapes with dimensions of

32 x 14 x 0.4 mm

(L x W x H), as shown in Figure

8a. The tensile tests were performed on a Zwick

Z010 machine with a 500 N load-cell and extension

rate of 1 mm/min for all specimens. Through the

measured stress-strain curve, both the elastic

modulus and tensile strength can be determined.

Figure 9 shows an exemplary stress-strain curve of

PDMS/CNTs membrane which has ~1% CNTs by

volume oriented perpendicular to the loading

direction. The tested membranes present an elastic

modulus of about 2.42 MPa (at the initial stage) and

rupture at around 0.87MPa. The pure PDMS has a

Young modulus of approximately 0.5 MPa.

Figure 9: Stress-Strain curve of a flexible PDMS

membrane with embedded CNTs.

5.2 Sensor Geometry

Equations (6) and (2) enable us to analytically

calculate the capacitance changes for a given applied

pressure on the sensor. An analytical model was

implemented using the two equations and was used

to design the sensor. The main concerns during the

design phase were related to the device thickness

(<=300 μm) and the capacitor total area (<=1.5

DESIGN OF A PRESSURE SENSOR FOR MONITORING OF POST-ENDOVASCULAR ANEURYSM REPAIR

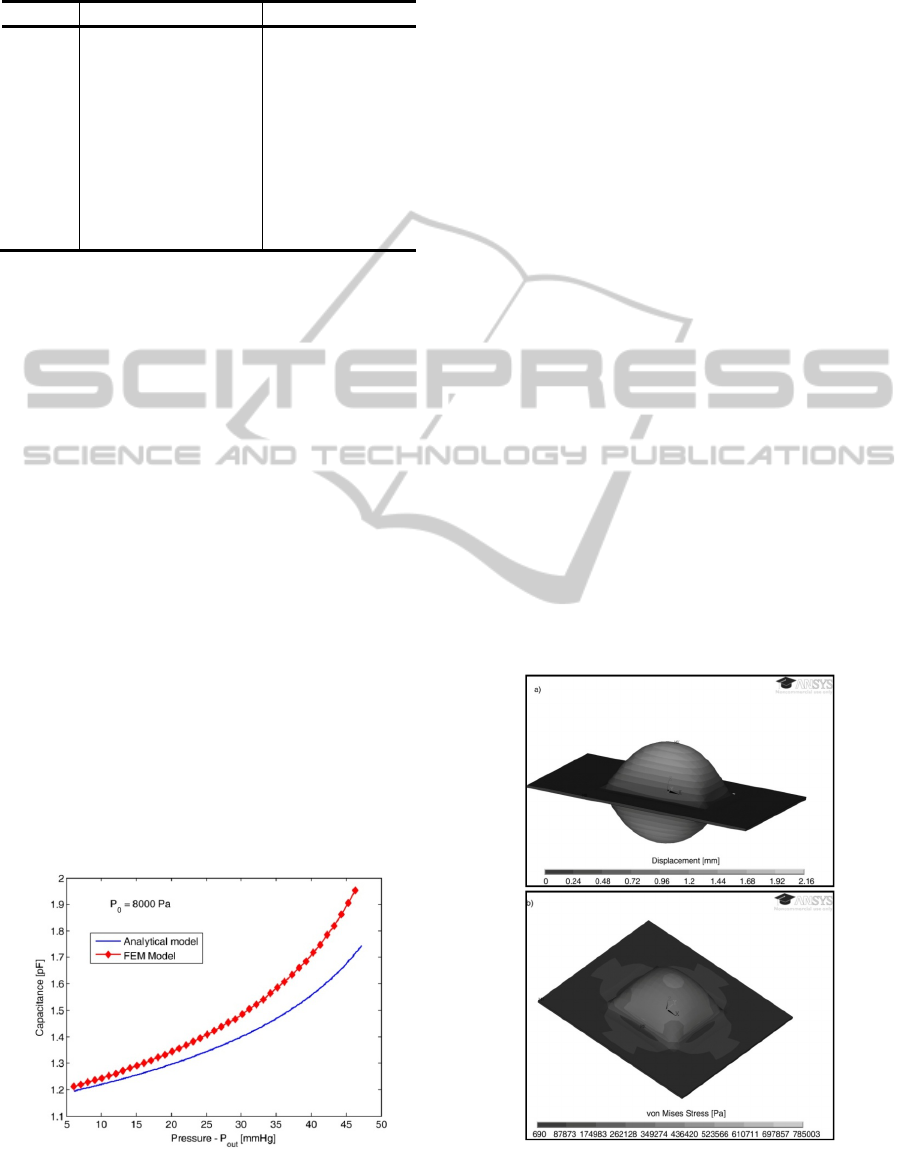
Table 2: Dimensions and material properties of the

pressure sensor.

Parameter Description Value

a radius 5 mm

distance between

electrodes

50 μm

Pressure of the sensor

cavity

8000 Pa

t diaphragm thickness 100 μm

E Elastic Modulus 2.42 MPa

Poisson’s ratio 0.48

relative permittivity 1

permittivity of free space 8.854x10

-12

F/m

An important characteristic of the sensor

behaviour is the sensitivity dependence on the

dielectric cavity pressure (P

). If the last bonding

step is performed in a pressure controlled

environment, P

can be controlled which allows the

realization of sensors with different sensitivities and

dynamic ranges. Table 2 presents the defined sensor

dimensions taking into account that for this

application, the pressure range to be measured is

around 6-16 mmHg, while Figure 10 presents the

expected capacitance changes using the analytical

model.

In order to validate the model, a Finite Element

Model (FEM) was developed in ANSYS using a

coupled domain (mechanical and electrostatic)

approach. The developed FEM model uses initially a

structural physical domain that computes the

bending due to applied pressure. Then, the command

dvmorph is issued and the non-structural areas are

re-meshed (taking into account the displacement of

the diaphragm due to pressure applied). Finally, an

electrostatic physical domain is used to calculate the

capacitance. The comparative results are presented

in Figure 10. The deviations between models are due

to the assumptions made during the derivation of the

analytical model.

Figure 10: Capacitance changes due to external pressure

changes.

Figure 11a shows the bending of the diaphragm for

an external pressure of 6mmHg and Figure 11b the

stress on the membranes.

5.3 Discussion

The results obtained raise three main concerns

regarding the suitability of the realization of a

pressure sensor with passive telemetry using the

proposed technology. The first one is related to the

rather low conductivity of the PDMS membranes

with embedded CNTs. The low conductivity will

generate a rather high resistance of the inductor and

therefore the energy transferred inductively will be

dissipated in the resistor. Solutions to overcome this

problem are already being studied, and the use of

inkjet-printed conductive inks seems to be a good

candidate. Alignment of the continuous CNTs in the

conduction direction is another option, as much

higher conductivities have been reported for PNCs.

A second concern is the low capacitive value (1-

2pF) of the proposed sensor geometry. While the

capacitive changes are within the desirable values,

the total capacitor value is lower than the required

one (see section 2). This problem can be easily

overcome by placing a fixed capacitor in parallel

(using the middle PDMS layer as dielectric) in such

a way that the total capacitance value is within the

required values (5-12pF). PNC morphology changes

may also be used to engineer this quantity as with

electrical resistivity above.

Figure 11: Results from the FEM model a) bending and b)

von Mises stress contours.

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

The third concern relates to the tensile strength

of the membranes. The measured rupture stress of

the samples (~0.87 MPa) is within the range of

stresses given by the FEM model. While the stresses

on the diaphragm are well below this value, the

stresses retrieved from the FEM model on the edges

of the diaphragm approach the membranes tensile

strength meaning that the devices can break during

operation. A solution to reduce the stress in the

edges could be to work on the mould in order to

avoid sharp edges (where stresses tend to

accumulate). Alternatively, one could try to increase

the tensile strength of the membranes by changing

the volume fraction and/or configuration of the

embedded aligned CNTs.

6 CONCLUSIONS

This paper introduces a new approach for the

pressure measurement within an aneurysm sac for

post-EVAR surveillance based on a highly flexible

pressure sensor. The pressure sensor is flexible and

thin so it can be placed on top of a stent-graft and

delivered during the EVAR procedure without the

requirement of an extra surgery step.

The characterization results of the new

introduced fabrication process are promising and

enable the realization of a pressure sensor that has

the required specifications (sensitivity and dynamic

range) for the application. Nevertheless, some

problems are foreseen that can jeopardize the final

implementation. This technology can find

applications in other fields such as e-textiles and

portable medical devices, opening the scope of the

current research.

The first sensor prototypes are under

development, and fully sensor characterization is

expected soon.

ACKNOWLEDGEMENTS

The first author wishes to thank FCT - Fundação

para a Ciência e Tecnologia, Portugal, for the

financial support provided by the grant SFRH/BD/

42922/2008. This work is supported by FCT under

the project MIT-Pt/EDAM-EMD/0007/2008. CNT-

based polymer composite materials were developed

with funding from Airbus S. A. S., Boeing, Embraer,

Lockheed Martin, Saab AB, Spirit AeroSystems,

Textron Inc., Composite Systems Technology, and

TohoTenax Inc. through MIT’s Nano-Engineered

Composite aerospace STructures (NECST)

Consortium.

REFERENCES

Ajayan, P. M., Schadler, L. S., Giannaris, C. and Rubio,

A. (2000), Single-Walled Carbon Nanotube–Polymer

Composites: Strength and Weakness. Advanced

Materials, 12, 750-753.

Bello, D., Hart, A. J., Ahn, K., Hallock, M., Yamamoto,

N., Garcia, E. J., Ellenbecker, M. J., Wardle, B. L.

(2008). Particle exposure levels during CVD growth

and subsequent handling of vertically-aligned carbon

nanotube films. Carbon, 46, 974-977.

Cebeci, H., Guzmán de Villoria, R., Hart, A. J., and B. L.

Wardle (2009). Multifunctional Properties of High

Volume Fraction Aligned Carbon Nanotube Polymer

Composites with Controlled Morphology. Composites

Science and Technology, 69, 2649-2656.

Chau, H.-L. and Wise, K. D. (1987). Scaling limits in

batch-fabricated silicon pressure sensors. IEEE Trans.

Electron Devices ED, 24, 850–858.

Chuter, T., Parodi, J. C. and Lawrence-Brown, M. (2004).

Management of abdominal aortic aneurysm: a decade

of progress. Journal of Endovascular Therapy,

11(Suppl II), S82-S95.

Eddings, M. A., Johnson, M. A., Gale, B. K. (2008).

Determining the optimal PDMS-PDMS bonding

technique for microfluidic devices. J. Micromech.

Microeng. 18, 067001.

Greenhalgh, R. M. (2005). Endovascular aneurysm repair

versus open repair in patients with abdominal aortic

aneurysm (EVAR trial 1): randomised controlled trial.

Lancet, 365(9478), 2179-2186.

Hart, J., Slocum, A. H. (2006). Rapid growth and flow-

mediated nucleation of millimeter-scale aligned

carbon nanotube structures from a thin-film cata-lyst.

Journal of Physical Chemistry B, 110, 8250-8257.

Hayter C. L., Bradshaw S. R., Allen R. J., Guduguntla M.

and Hardman D. T. (2005). Follow-up costs increase

the cost disparity between endovascular and open

abdominal aortic aneurysm repair. Journal of Vascular

Surgery, 42(5), 912-918.

Katzen, B. T. and MacLean, A. A. (2006). Complications

of endovascular repair of abdominal aortic aneurysms:

A review. CardioVascular and Interventional

Radiology, 29(6), 935-946.

Li, Z. and Kleinstreuer, C. (2006). Analysis of

biomechanical factors affecting stent-graft migration

in an abdominal aortic aneurysm model. J. of

Biomechanics, 39 (12), 2264-73.

Michaels, J. A., Drury, D. and Thomas, S. M. (2005).

Cost-effectiveness of endovascular abdominal aortic

aneurysm repair. British Journal of Surgery, 92, 960-

967.

Milner, R., Kasirajan, K. and Chaikof, E. L. (2006). Future

of endograft surveillance. Seminars in Vascular

Surgery, 19(2), 75-82.

DESIGN OF A PRESSURE SENSOR FOR MONITORING OF POST-ENDOVASCULAR ANEURYSM REPAIR

Mokwa, W. (2007). Medical implants based on

Microsystems. Meas. Sci. Technol., 18, R47-R57.

Myers, K., Devine, T., Barras, C., Self, G. (2001).

Endoluminal Versus Open repair for abdominal aortic

aneurysms. 2nd Virtual Congress of Cardiology.

Parodi, J. C., Palmaz, J. C. and Barone, H. D. (1991).

Transfemoral intraluminal graft implantation for

abdominal aortic aneurysms. Annals of Vascular

Surgery, 5(6), 491-499.

Potkay, J. A. (2008). Long term, implantable blood

pressure monitoring systems. Biomed Microdevices,

10, 379–392.

Receveur, R. A. M., Lindemans, F. W. and de Rooij, N .F.

(2007). Microsystems technologies for implantable

applications. J. Micromech. Microeng., 17, R50-R80.

Rutherford, R. B. and Krupski, W. C. (2004). Current

status of open versus endovascular stent-graft repair of

abdominal aortic aneurysm. Journal of Vascular

Surgery, 39(5), 1129-1139.

Springer, F., Günther, R. W. and Schmitz-Rode, T. (2007).

Aneurysm sac pressure measurement with minimally

invasive implantable pressure sensors: An alternative

to current surveillance regimes after EVAR?.

CardioVascular and Interventional Radiology, 31(3),

460-467.

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices