
AUTOMATED COUNTING OF YEAST COLONIES USING
THE FAST RADIAL TRANSFORM ALGORITHM
Jan Schier and Bohumil Kov
´
a
ˇ
r
Institute of Information Theory and Automation of the ASCR, Pod vod
´
arenskou v
ˇ
e
ˇ
z
´
ı 4
CZ-182 08 Prague 8, Czech Republic
Keywords:
Colony counter, Yeast colonies, Image segmentation, Fast radial transform.
Abstract:
A method for counting yeast colonies in images of Petri dishes, based on the fast radial transform by Loy
and Zelinsky, is introduced and evaluated in the paper. The paper focuses on processing images produced
by a general-purpose imaging setup. The characteristic properties of the images, as produced by the setup
used in the cooperating genetics research laboratory, are described. The performance of the method has been
evaluated with a test set of 245 images. The images, included in this set, typically contained between 10 and
70 colonies per dish, with relative coverage of the dish less than 10% of the area. The average counting error
(missed colonies) on this set was under 4%.
A tool, implementing the method, has been developed in Matlab. The tool provides a batch mode for pro-
cessing of larger image sets prepared beforehand in the darkroom and it automates the process of counting as
much as possible. It is available for download or can be requested from the authors of the paper, in both cases
free on charge.
1 INTRODUCTION
Yeast, namely Saccharomyces cerevisiae, is often
used as a model organism in biological research. This
is mainly due to its many favourable properties, such
as the short generation time, easy genetical manipula-
tion, as well as thanks to its established use in indus-
try.
When performing experiments with S. Cerevisiae
yeast, part of the process is growing the yeast colonies
in Petri dishes, and evaluating the growth parame-
ters, such as the coverage of the dish and the num-
ber of colonies. Traditionally, the colonies have
been counted manually, using either manual colony
counter or a counting raster. Examples of the man-
ual counters are the Colony counter SC6 by Stu-
art (www.stuart-equipment.com) or the EW-14211-02
Hand-Held Electronic Colony Counter from Cole-
Parmer (www.coleparmer.com). However, the hand
counting is considered rather laborious and time-
consuming process, error prone due to the fatigue and
eye-strain of the laboratorian. Also, it does not pro-
vide any figures on the coverage of the dish or the
radii of the colonies.
There are also a number of automated colony
counters available – it is of interest that such sys-
tem has been described as early as in 1974 (Goss
et al., 1974). Such system usually consists of a single-
purpose chamber with the illumination and camera
system, where the dishes are placed one-by-one, or of
an automated plate-handler, and a computer running
an image-processing program that performs thresh-
olding and segmentation of the image.
While an automated counter is definitely the
system-of-choice for a commercial lab, in our case,
the requirement was to reuse the imaging equipment
already available in the lab (to achieve a low-cost so-
lution) and to provide an off-line batch processing of a
set of images taken beforehand in the darkroom. Also,
the goal was that the system performs adequately for
typical image variations, as described in the next sec-
tion, with minimum possible manual intervention of
operator. At the same time, it should allow for man-
ual correction of the counting errors (multiple detec-
tions of a single colony or missed colonies). Finally,
it should provide not only the count of colonies, but
also evaluate the total coverage of the dish.
In this paper, we focus on the counting algorithm
used in the system and present the performance data
that we have achieved. The paper is structured in the
following way: in the next section, the characteristics
of typical images are reviewed. Then, the methods for
22
Schier J. and Ková
ˇ
r B..
AUTOMATED COUNTING OF YEAST COLONIES USING THE FAST RADIAL TRANSFORM ALGORITHM.
DOI: 10.5220/0003129000220027
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 22-27
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

(a) Fluffy and touching colonies, di-
verse radii, dish centered
(b) Smooth colonies, dish touching
edge of image
Figure 1: Examples of typical images of yeast colonies.
detecting round or symmetrical objects are surveyed
in brief and the fast radial transform algorithm is de-
scribed. The paper is concluded by description of the
properties of the test data set and by discussion of the
achieved results.
2 CHARACTERISTICS OF
TYPICAL IMAGES
As has been stated, the requirement on the system de-
scribed in this paper was that it would be able to pro-
cess batches of images taken with a simple general-
purpose imaging system; the laboratory is using a
camera/copy stand with lightning units by Kaiser Fo-
totechnik (see www.kaiser-fototechnik.de). The dishes
are manually placed roughly into the center of the im-
age, on a matt black background. No dish holder or
stopper is used.
Examples of typical images of yeast colonies are
shown in Figure 1.
The images are characterized by the following
properties:
• dark background to increase image contrast
• illumination by two linear lights along the short
edges (this is not important for processing,
though)
Figure 2: Dish image after preprocessing.
• variations of dish position – cf. Figure 1(a) and
1(b)
• varying diameter of the dish in image
• varying intensity of the dish background
The colonies themselves are characterized by differ-
ent types of morphologies (both smooth and fluffy),
different size and/or age and by colonies touching
each other.
3 SYSTEM DESCRIPTION
It follows from the image characteristics that the
counting of colonies includes image thresholding,
dish localization, and the counting itself. The process
can be divided into two basic parts:
• Image Preprocessing – includes the following op-
erations:
– Image quality check: faulty images are elimi-
nated to prevent system hangup
– Image thresholding
– Dish localization
– Dish background thresholding
As a result of preprocessing, we get a centered im-
age of the dish, with eliminated background. An
example of such image is given in Figure 2.
• Colony Counting – includes:
– colony diameter estimation
– colony center estimation
The description of the preprocessing part is out of
the scope of this paper. Interested reader may find
some details in technical report (Schier, 2009b). The
method, however, has been simplified and made more
robust since the publication of this report.
AUTOMATED COUNTING OF YEAST COLONIES USING THE FAST RADIAL TRANSFORM ALGORITHM
23

3.1 Colony Counting
The simplest approach is to correlate the contour of
the colonies with a circular pattern, assuming that
the maxima of correlation is located at the centers
of colonies. This has been the first method we have
tested (Schier, 2009a). During experiments, we have
experienced poor performance in the case of big clus-
ters and sensitivity to mismatch between the radius
of the circular pattern diameter and the radius of the
colony (and, hence, sensitivity to dispersion of colony
radii).
An interesting approach to the counting of bac-
teria colonies has been described in (Marotz et al.,
2001): to find colonies, a number of shape and struc-
ture criteria are used on the image pixels, including
e.g. mean object radius, roundness of an object, com-
pactness and asymmetry, radial monotony of fall-off
in intensity, etc. These criteria are combined into
shape and structure quality parameters and evaluated
using fuzzy logic. The method works best under the
assumptions of well-defined circular shape and mono-
tone intensity fall-off of the colonies, which are well
satisfied for bacteria (the case treated in the paper),
but not necessarily in our case of the yeast colonies.
A popular method to detect circular objects is the
circular Hough transform (for definition see e.g. (Bal-
lard and Brown, 2003)). Based on our experiments, if
multiple yeast colonies are overlapping or touching,
it tends to detect (incorrectly) adjacent colonies as a
single object. Also, following the results presented
in (Loy and Zelinsky, 2003), the output of the Hough
transform may be rather noisy.
Another possibility is to use the radial symme-
try-based methods: the radial symmetry transform
has been introduced in the work of Reisfeld (Reis-
feld et al., 1995). Fast radial transform – a modi-
fied version of the radial symmetry transform with
improved computational complexity – has been pre-
sented in (Loy and Zelinsky, 2003). Since this trans-
form is the method that is currently employed in our
tool, it will be reviewed in the next section.
3.1.1 Fast Radial Transform
Fast Radial Transform is a transform that maps the
original image to the transformed image according to
its contribution to radial symmetry of the gradients at
distance n ∈ N (N is the set of radii) away from each
point. For full details of the method see the original
description in the paper of Loy and Zelinsky.
First, image gradient g
i,j
at each point (i, j) is cal-
culated. Then, the positively- and negatively-affected
pixels are determined:. The affected pixel is defined as
the point in the direction of the gradient vector g
i, j
is
(for the positively-affected ones) or counter the direc-
tion of the gradient vector (for the negatively-affected
ones), at a distance n pixels away from the point at
coordinates (i, j). The coordinates of affected pixels
are given by
p
+
(i, j) = (i, j) + round
g
i, j
kg
i, j
k
n
p
−
(i, j) = (i, j) − round
g
i, j
kg
i, j
k
n
The gradient matrix g, together with the coordi-
nates of affected pixels, is used to determine the ori-
entation and magnitude projection images O
n
and M
n
for the given radius n:
O
n
(p
+
(i, j)) = O
n
(p
+
(i, j)) + 1,
O
n
(p
−
(i, j)) = O
n
(p
−
(i, j)) − 1,
M
n
(p
+
(i, j)) = M
n
(p
+
(i, j)) + kg
i, j
k,
M
n
(p
−
(i, j)) = M
n
(p
−
(i, j)) − kg
i, j
k.
The radial symmetry at radius n is defined by con-
volution
S
n
= F
n
∗ A
n
,
where
F
n
(i, j) =
M
n
(i, j)
k
n
|
˜
O
n
(i, j)|
k
n
α
,
and
˜
O
n
(i, j) =
(
O
n
(i, j) i f O
n
(i, j) < k
n
k
n
otherwise.
A
n
is a two-dimensional Gaussian, α is the radial
strictness parameter and k
n
is a scaling factor used to
normalize M
n
and O
n
. Projection images M
n
and O
n
are initially set to zero.
An example of a symmetry map for a dish with
yeast colonies is given in Figure 3.
To estimate the colony centers, the transform must
be completed with two additional procedures: esti-
mation of the set of radii N to be tested, and by a
procedure to find local maxima (corresponding to the
centers) in the symmetry map S (map S is a weighted
sum of all symmetry maps S
n
). Both procedures will
be discussed in the following sections.
3.1.2 Colony Radius Estimation
To estimate the range of radii of the objects contained
in the image, the following steps are used:
• the equivalent diameter d and eccentricity ε of all
objects in the image is computed. The diameter
is computed from area A (number of pixels) of an
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
24
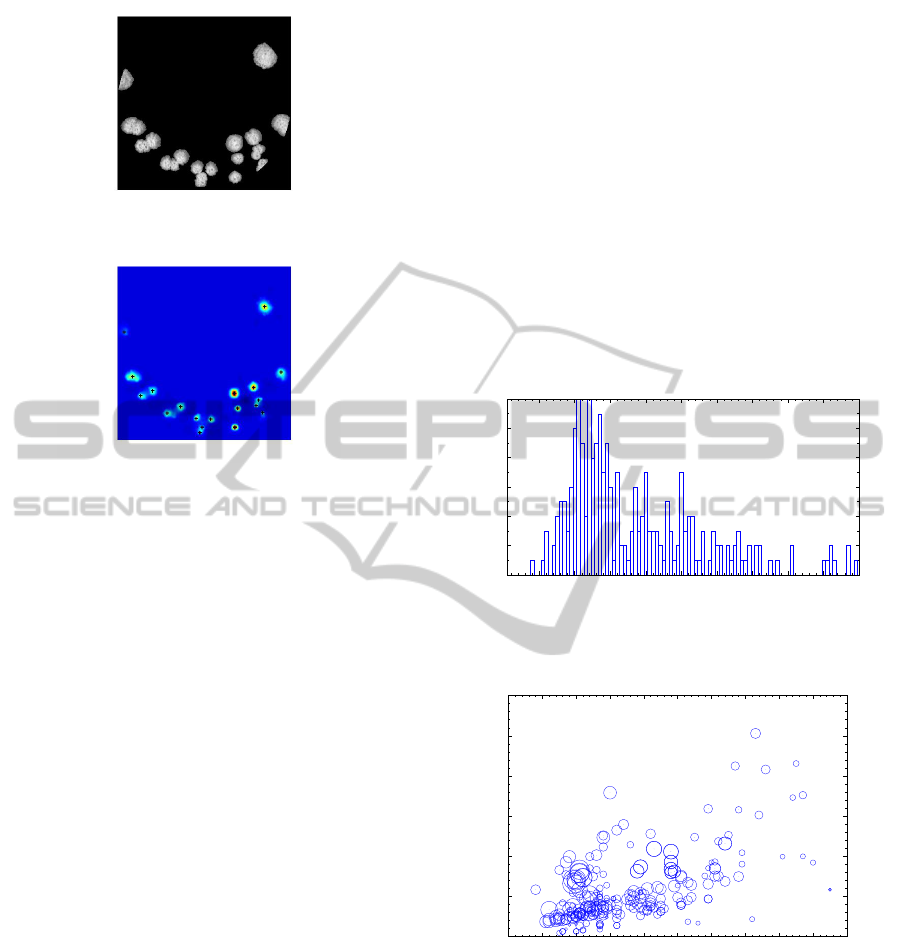
(a) Preprocessed image of colonies
(b) Symmetry map S with the centers of
colonies
Figure 3: Illustration of function of the radial symmetry al-
gorithm.
object. The eccentricity equals to the eccentricity
of an ellipse with the same second-moments as the
object. It equals to ε = 0 for a circle and to ε = 1
for a line segment.
• Nearly circular objects (with eccentricity ε < θ
ε
,
θ
ε
is the eccentricity threshold), are selected.
• Min and max diameter d
min
and d
max
of the ob-
jects in the set of circular objects are determined.
The interval between them is divided to ν equidis-
tant subintervals. The set of radii N for the fast
radial transform is then given by:
∆ = d
max
− d
min
N = {d
min
+ [0,...,ν] · ∆/ν}/2
3.1.3 Estimation of Colony Centers
The centers of the colonies are represented by local
maxima of the symmetry matrix S. To find these
maxima, the nonmaxsuppts() function for Matlab
(Kovesi, 2005) is used. It performs grey scale dilation
of the input image and finds the points in the dilated
image that match the original and that are greater than
the threshold. Finally, it returns the row and column
coordinates of these points.
4 EXPERIMENTS AND RESULTS
To test system recognition performance, it was evalu-
ated using 245 images, containing colonies with dif-
ferent morphology and relative coverage of the dish.
The distribution of the test set in the terms of fre-
quencies of the number of colonies in the dish is
shown in Figure 4. Figure 5 shows the distribution
of relative coverage of the dish and mean diameter of
colonies (marker size) in comparison with the number
of colonies in the dish. It can be seen that the typical
dish contains less than 70 colonies, with relative cov-
erage less than some 10%.
The illustrative counting results for typical images
used in these tests are shown in Figure 6 on the next
page.
0
2
4
6
8
10
12
10 20 30 40 50 60 70 80 90 100
Occurrences
Number of colonies
Figure 4: Petri dishes with the same number of yeast
colonies.
0
5
10
15
20
25
30
0 10 20 30 40 50 60 70 80 90 100
Relative area [%]
Number of colonies
Figure 5: Distribution of the test set – relative dish coverage
in comparison with the number of colonies. Diameter of
markers represents mean radius of the colonies in the dish.
4.1 Counting Tool
The algorithms, as described in Section 3, have been
implemented in a counting tool. In the background,
this tool performs fully automatic thresholding of
the image, localization of the dish and counting of
colonies. It provides an environment for selecting the
directory tree with images to process, the file to store
AUTOMATED COUNTING OF YEAST COLONIES USING THE FAST RADIAL TRANSFORM ALGORITHM
25

(a) (b)
(c) (d)
Figure 6: Examples of algorithm detection and counting re-
sults. Figures (a) - (b) illustrate dishes with high coverage,
(c) - (d) dishes with low coverage.
the counting results, and the counting mode: in the
semi-automatic mode, a simple point-and-click editor
can be used for manual correction of the output of the
counting algorithm, in the fully-automatic mode, the
output of algorithm is directly stored into the result
file.
This tool was used also to obtain the reference re-
sults used in this paper: using manual correction, we
obtained the correct counts of colonies in Petri dishes,
which were used to evaluate counting error rates.
4.2 Algorithm Settings
The following settings were used in our experiments:
• Parameters of the fast radial transform:
k
n
= 6, α = 4
• Parameters of non-maxima suppression:
threshold = 4, radius = 0.8 · min(N),
where N is the set of radii for the fast radial trans-
form.
• Construction of N:
eccentricity threshold θ
ε
(see Section 3.1.2) is ini-
tially set to θ
ε
= 0.25. The number of equidistant
intervals ν is set to ν = 4. At least five colonies of
given eccentricity must be in the image, else the
eccentricity is increased by 0.1.
4.3 Typical Detection Errors
Figure 7 illustrates typical detection errors of fast ra-
dial transform. A colony may be missed if it touches
other colony or, rather, multiple colonies, so that they
form a cluster. This detection error is almost absent if
the colonies touch only at one point and thus creates
a structure similar to a chain. If more colonies are
touching each other, they form a structure in which
their shape is distorted and internal colonies cease to
be circular. The circular outer border of colony lo-
cated in such cluster could be too short for the pro-
posed method to work properly.
(a) (b)
Figure 7: Example of typical detection error of fast radial
transform.
The counting errors for various number of
colonies are summarized in the Table 1. The relatively
high counting error for the dishes with the colony
counts greater than 60 is given by two factors. First,
with the increasing number of colonies increases also
the probability that there will be colonies touching
each others (Figure 7a). Second, the number of sam-
ples with this high density of coverage was relatively
low, thus increasing the evaluation error (Figure 4).
Table 1: Dependence of the counting errors on the number
of colonies in the dish. The system average counting error
is under 4%
] colonies samples missed [%] false [%]
0 – 17 21 1.47 0
18 – 20 19 2.99 0
21 – 23 25 3.31 0
24 – 26 29 4.00 0
27 – 29 27 3.28 0
30 – 40 35 4.17 0
41 – 49 30 4.00 0
50 – 60 29 3.87 2.00
> 60 30 5.36 3.22
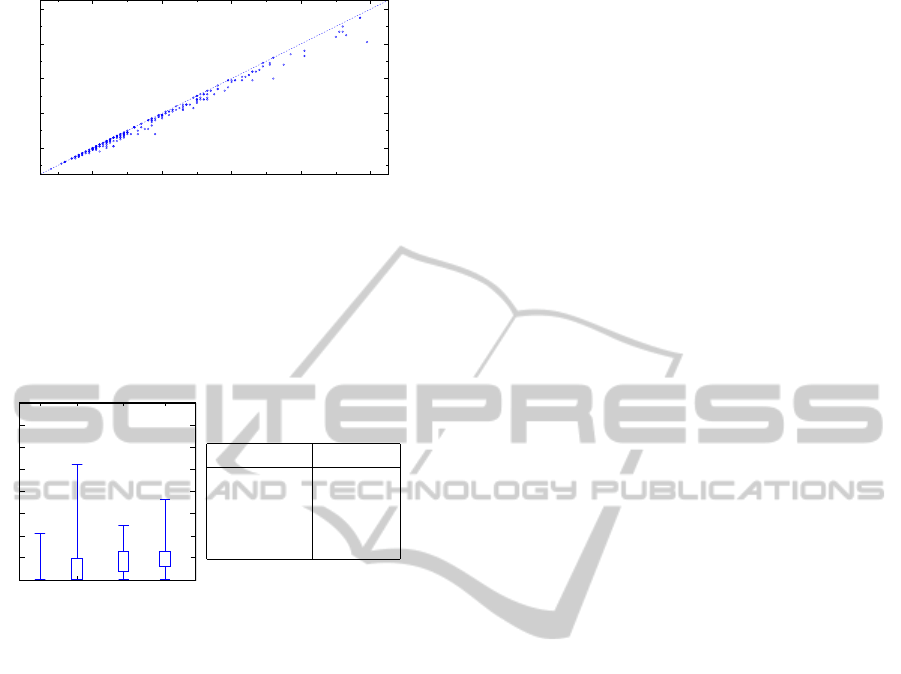
Figure 8 shows the recognition performance re-
lated to the number of colonies in the dish. A typical
dish used in our experiments contains from 10 to 40
yeast colonies. The figure also shows the recognition
performance of the fast radial transform for the de-
tection of circular objects. The dishes, where some
colonies have not been detected are shown below the
dashed line.
Another view on the algorithm performance is
provided by Figure 9, which presents a box-whisker
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
26
20
40
60
80
100
20 40 60 80 100
Number of detected colonies
Number of colonies
Figure 8: Algorithm recognition performance regarding to
number of colonies.
plot of relative counting error (missed colonies) in
several groups of the colony counts. The numbers of
samples in each group are given in the table, included
with this plot.
0
5
10
15
20
25
30
35
40
0-20 20-40 40-60 >60
Missed colonies (normalized) [%]
Number of colonies
# colonies samples
0–20 40
20–40 123
40–60 52
>60 30
Figure 9: Relative number of missed colonies dependent on
the number of colonies.
5 CONCLUSIONS
In the paper, we have presented the method for count-
ing of yeast colonies, based on fast radial transform.
The method has been tested on a set of 245 images
with different degrees of coverage. The distribution
of the data in the test set and the performance of the
counter is discussed. It should be noted that the av-
erage counting error is below 4%. It is difficult to
compare the performance with the commercial solu-
tions, since the performance data of these systems are
not available.
The algorithm has been implemented in a
Matlab-based tool which provides environment
for automatic or semi-automatic processing of
batches of images. This tool has been suc-
cessfully deployed in the cooperating biology
research laboratory and is available for download at
http://zs.utia.cz/index.php?ids=results&id=yeastcolco
unt&lang=enghttp://zs.utia.cz/index.php?ids=results&
id=yeastcolcount&lang=eng.
ACKNOWLEDGEMENTS
This research has been supported from the 1M0567
”Centre for Applied Cybernetics” project of the Min-
istry of Education, Youth and Sports, the Czech Re-
public.
We would like to thank the staff of the Yeast
Colony Group, Department of Genetics and Micro-
biology, Faculty of Sciences, Charles University, who
have introduced us into the problem and provided us
with the sample images from their experiments.
REFERENCES
Ballard, D. H. and Brown, C. M. (2003). Computer Vision.
Online Book.
Goss, W. A., Michaud, R. N., and McGrath, M. B. (1974).
Evaluation of an automated colony counter. Appl Mi-
crobiol, 27:264–267.
Kovesi, P. D. (2005). MATLAB and Octave functions
for computer vision and image processing. School
of Computer Science & Software Engineering,
The University of Western Australia. Available
from: http://www.csse.uwa.edu.au/∼pk/research/
matlabfns/.
Loy, G. and Zelinsky, A. (2003). Fast radial symmetry for
detecting points of interest. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 8(25):959–
973.
Marotz, J., L
¨
ubert, C., and Eisenbeiss, W. (2001). Effective
object recognition for automated counting of colonies
in petri dishes (automated colony counting). Com-
puter Methods and Programs in Biomedicine, 66(2–
3):183–198.
Reisfeld, D., Wolfson, H., and Yeshurun, Y. (1995).
Context-free attentional operators: The generalized
symmetry transform. International Journal of Com-
puter Vision, 14(2):119–130.
Schier, J. (2009a). Counting of yeast colonies in petri dish
images. Technical report, Inst. of Information Theory
and Automation of the ASCR. Also available online at
http://zs.utia.cz/index.php?ids=results&id=dishcount.
Schier, J. (2009b). Preprocessing of images of petri dishes.
Technical report, Inst. of Information Theory and Au-
tomation of the ASCR. Also available online at
http://sp.utia.cz/index.php?ids=results&id=dishprep.
AUTOMATED COUNTING OF YEAST COLONIES USING THE FAST RADIAL TRANSFORM ALGORITHM
27
