METABOLIC MODELING OF CONVERGING METABOLIC

PATHWAYS

Analysis of Non-steady State Stable Isotope-resolve Metabolism

of UDP-GlcNAc and UDP-GalNAc

Hunter N. B. Moseley, Richard M. Higashi, Teresa W-M. Fan

Department of Chemistry, University of Louisville, 2320 S Brook Street, Louisville, KY 40292, U.S.A.

Structural Biology Program, JG Brown Cancer Center, University of Louisville, Louisville, KY 40202, U.S.A.

Andrew N. Lane

Department of Chemistry, University of Louisville, 2320 S Brook Street, Louisville, KY 40292, U.S.A.

Structural Biology Program, JG Brown Cancer Center, University of Louisville, Louisville, KY 40202, U.S.A.

Department of Medicine, Clinical Translational Research Building, 505 S. Hancock St., Louisville KY 40202, U.S.A.

Keywords: Metabolic modelling, Systems biochemistry, Model optimization, Model selection, Non-steady state,

Stable isotope-resolved metabolomics, SIRM, GAIMS, Mass spectrometry, UDP-GlcNAc, UDP-GalNAc.

Abstract: We have developed a novel metabolic modeling methodology that traces the flow of functional moieties

(chemical substructures) through metabolic pathways via the deconvolution of mass isotopologue data of

specific metabolites. We have implemented a general simulated annealing/genetic algorithm for parameter

optimization called Genetic Algorithm for Isotopologues in Metabolic Systems (GAIMS), with a model

selection method developed from the Akaike information criterion. GAIMS is tailored for analysis of ultra-

high resolution, high mass-accuracy isotopologue data from Fourier transform-ion cyclotron resonance mass

spectrometry (FT-ICR-MS) for interpretation of non-steady state stable isotope-resolved metabolomics

(SIRM) experiments. We applied GAIMS to a time-course of uridine diphospho-N-acetylglucosamine

(UDP-GlcNAc) and uridine diphospho-N-acetylgalactosamine (UDP-GalNAc) isotopologue data obtained

from LNCaP-LN3 prostate cancer cells grown in [U-

C]-glucose. The best metabolic model was identified,

which revealed the relative contribution of specific metabolic pathways to

C incorporation from glucose

into individual functional moieties of UDP-GlcNAc and UDP-GalNAc. Furthermore, this analysis allows

direct comparison of MS isotopologue data with NMR positional isotopomer data for independent

experimental cross-verification.

1 INTRODUCTION

Modeling of cellular metabolism is a well-

established technique for studying the flow of matter

and energy through cells for a variety of purposes

including: i) understanding cellular growth (Edwards

et al., 2001), ii) determining the effects of gene and

signalling pathways on cellular metabolism (Sauer,

1999); and iii) detection of biomarkers (Harrigan

and Goodacre, 2003). Several common and related

modeling techniques such as metabolic balance

analysis (Fell, 1984; Savinell and Palsson, 1992;

Kaufman et al., 2003) and metabolic control analysis

(Fell, 1997; Stephanopoulos, 1999; Hellerstein,

2003; Sauer, 2006) have been developed which use a

series of differential equations to model the flux of

metabolites. These techniques typically require

steady-state conditions that allow the application of

standard numerical methods to solve a system of

differential equations in the form of an eigensystem.

While steady-state conditions are often assumed, in

reality they are quite hard to establish, maintain, and

verify for actual experiments involving mammalian

cells. For multicellular organisms, steady state

conditions for all metabolites are practically

impossible to establish. Also, most applications of

108

N. B. Moseley H., M. Higashi R., W-M. Fan T. and N. Lane A..

METABOLIC MODELING OF CONVERGING METABOLIC PATHWAYS - Analysis of Non-steady State Stable Isotope-resolve Metabolism of

UDP-GlcNAc and UDP-GalNAc.

DOI: 10.5220/0003129401080115

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 108-115

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Structure of UDP-GlcNAc labeled by its functional moieties and their biosynthetic pathways from a [U-

C]-

glucose source. Uracil moiety is derived from glycolysis, citric acid cycle and pyrimidine biosynthesis. Ribose moiety is

derived from the pentose phosphate pathway and pyrimidine biosynthesis. A

cetyl moiety is derived from glycolysis.

lucose moiety is directly incorporated. UDP-GalNAc has an identical structure and pathway derivation with glucose

replaced by its isomer G

alactose.

Figure 2: Converging metabolic pathways leading from [U-

C]-glucose to UDP-GlcNAc and UDP-GalNAc.

C-labeled

glucose is incorporated into the nucleotide sugars via four routes: i) direct incorporation via the right UDP-hexose

biosynthetic pathway; ii) via glycolysis; iii) via glycolysis, citric acid acid cycle, and pyrimidine biosynthesis; and iv) via

the pentose phosphate pathway and pyrimidine biosynthesis.

these modelling techniques rely on total metabolite

concentrations or isotopic ratios derived from

experiment, which creates an underdetermined

system of equations where there are more variables

than independent data. Thus, unique meaningful

solutions to these numerical systems are not always

possible (Schellenberger and Palsson, 2009) and

their use in testing model validity is therefore

limited.

Using stable isotope resolved metabolomics

(SIRM) to determine individual isotopomers and

isotopologues detected by NMR and mass

spectrometry, respectively, can greatly increase the

ratio of experimental data to equation variables

(Lane et al., 2009). Supplying [U-

C]-glucose to

cells in culture allows each carbon in a detected

metabolite to be a separate sensor for

incorporation. However, detection, resolution, and

unique identification of individual isotopologues

requires the ultra-high mass accuracy provided by

FT-ICR-MS (Lane et al., 2008; Lane et al., 2009;

Moseley, 2010). Moreover, steady-state conditions

are even harder to establish with isotopomer and

isotopologue data (Lane et al., 2009), and may be

undesirable when one seeks to maximize the

information content of the data (Wahl et al., 2008).

Since steady-state conditions for SIRM

experiments are neither achievable, nor desirable in

mammalian cells, we have developed a novel

metabolic modeling methodology that interprets

isotopologue data of detected metabolites as flows of

functional moieties through metabolic pathways.

Such moieties correspond to actual, individual

biochemical entities, rather than sums of species.

These moiety models are optimized using a

combined simulated annealing genetic algorithm

METABOLIC MODELING OF CONVERGING METABOLIC PATHWAYS - Analysis of Non-steady State Stable

Isotope-resolve Metabolism of UDP-GlcNAc and UDP-GalNAc

109

called Genetic Algorithm for Isotopologues in

Metabolic Systems (GAIMS). GAIMS optimizes

model variables to fit a given moiety model to

isotopologue data of specific metabolites obtained

from non-steady state SIRM experiments.

We used GAIMS to optimize moiety models

against time-course isotopologue data for UDP-

GlcNAc and UDP-GalNAc obtained from LNCaP-

LN3 prostate cancer cells grown in [U-

C]-glucose.

Metabolic control of UDP-GlcNAc and UDP-

GalNAc underlies the regulation of many biological

processes via O-linked glycosylation of proteins,

including nutrient sensing, protein degradation, gene

expression (Hart et al., 2007), and embryogenesis

(Gambetta et al., 2009). UDP-GlcNAc and UDP-

GalNAc are composed of four functional moieties as

shown in Figure 1: glucose or galactose, ribose,

acetyl, and UDP. These four functional moieties

represent the convergence of several major

metabolic pathways that lead from [U-

C]-glucose

to UDP-GlcNAc and UDP-GalNAc biosynthesis as

shown in Figure 2. These pathways include

glycolysis, the citric acid cycle, the pentose

phosphate pathway, pyrimidine biosynthesis, and the

UDP-hexose biosynthetic pathway referred to as the

“direct” pathway. Furthermore, other carbon sources

can contribute to the synthesis of the uracil and

acetyl moieties, to an extent that is cell and

condition dependent. The moiety modeling seeks to

determine the relative contributions for each

pathway segment.

UDP-GlcNAc and UDP-GalNAc are handled

together in this analysis because as these two

metabolites have identical mass-to-charge ratios, the

isotopologue peak intensities are the sum of both

metabolites. However, from NMR isotopomer

analysis (data not shown), UDP-GlcNAc is the

major contributor to the isotopologue intensities and

that this contribution is proportional across the set of

isotopologue peaks. This makes logical sense

because UDP-GlcNAc and UDP-GalNAc are

separated by a single reversible enzymatic reaction

catalyzed by the UDP-glucosamine epimerase.

2 METHODS

2.1 Data Acquisition and Natural

Abundance Correction

LNCaP-LN3 prostate cancer cells (donated from

Roswell Park) were grown to 70% confluence at 37º

C in RPMI 1640 medium supplemented with: 10%

FBS, 100 units/mL penicillin, 100 µg/mL

streptomycin, 0.2% glucose, and 5% CO

. Next,

medium was replaced with a similar RPMI 1640

medium containing 0.2% [U-

C] glucose. Cells

were harvested at different time points, centrifuged,

extracted with 10% trichloroacetic acid, lyophilized,

and dissolved in H

O. These samples were then

analyzed via direct infusion nanoelectrospray FT-

ICR-MS in negative ion mode using a Thermo 7T

LTQ FT-MS. Isotopologue peaks were assigned

using the software PREMISE (Lane et al., 2009) and

each peak intensity was measured and normalized to

the sum of the isotopologue intensities:

obs

= I

raw

/Σ I

raw

(1)

Finally, the set of UDP-GlcNAc and UDP-

GalNAc isotopologue intensities were corrected for

C natural abundance using the following three

equations implemented in an iterative algorithm

(Moseley, 2010).

(2)

(3)

(4)

2.2 Moiety Modeling

As is shown in Figure 1, UDP-GlcNAc is composed

of four functional moieties, glucose, ribose, acetyl,

and uracil, representing convergence of several

metabolic pathways. We can represent each moiety

as a set of state variables reflecting the probabilities

C incorporation into each moiety. The state

variables g0,r0,a0,u0 represent the probability of no

C incorporation in glucose, ribose, acetyl, and

uracil, respectively. From Figure 2, it seems

reasonable to restrict

C incorporation for glucose,

ribose, and acetyl to the fully labelled state variables

g6, r5, and a2, respectively. This is experimentally

corroborated by the absence of partially labelled

isotopomers of glucose, ribose, and acetate.

Naturally, then the following relationships hold for

the state variables of glucose, ribose, and acetyl:

g6 = 1 – g0

r5 = 1 - r0

a2 = 1 – a0

(5)

However, the biosynthesis of uracil mixes

from labelled glucose via

-acetyl-CoA with

from other (unlabeled) sources during the citric acid

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

110

cycle. Thus, multiple state variables u1,u2, and u3

must be used to represent the partial labelling of

uracil. There is no u4 state variable since one carbon

of uracil is derived from unlabeled CO

. These state

variables have the following relationship:

u0 + u1 + u2 + u3 = 1 (6)

The state variables for all four moieties can

describe the probabilities for 32 different

isotopomers of UDP-GlcNAc and the intensities for

18 isotopologues via the following set of equations:

= g0r0a0u0

= g0r0a0u1

= g0r0a0u2 + g0r0a2u0

= g0r0a0u3 + g0r0a2u1

= g0r0a2u2

= g0r5a0u0 + g0r0a2u3

= g6r0a0u0 + g0r5a0u1

= g6r0a0u1 + g0r5a2u0 + g0r5a0u2

= g6r0a2u0 + g6r0a0u2 + g0r5a0u3 + g0r5a2u1

= g6r0a0u3 + g6r0a2u1 + g0r5a2u2

= g6r0a2u2 + g0r5a2u3

= g6r5a0u0 + g6r0a2u3

= g6r5a0u1

= g6r5a0u2 + g6r5a2u0

= g6r5a0u3 + g6r5a2u1

= g6r5a2u2

= g6r5a2u3

= NA contribution only

(7)

In addition, these state variables and their

constraining relationships provide six optimizable

parameters (g6, r5, a2, u1, u2, u3), one each for

glucose, ribose, and acetyl and three for uracil.

These variables are time dependent, and constitute

the starting point for detailed flux analysis of the

specific metabolic network that described the

synthesis of the observed product.

2.3 GAIMS

To extract the variables from the data, we have

developed a combined simulated annealing and

genetic algorithm called Genetic Algorithm for

Isotopologues in Metabolic Systems (GAIMS) to

optimize moiety model parameters. GAIMS uses a

description of the moiety model to calculate

isotopologue intensities (Equations 7). The program

then uses these calculated isotopologue intensities

n,calc

) with the observed experimental isotopologue

intensities (I

n,obs

) to create a target function that

compares calculated isotopologue intensities to their

experimentally observed counterparts:

target_function = Σabs(I

obs

– I

calc

)

(8)

Other target functions were tested including the

commonly used sum of squared differences;

however, that function tended to fit stronger

isotopologue intensities at the expense of weaker

isotopologue intensities. Also, target functions

normalized by intensity demonstrated poorer

convergence, probably due to the higher fractional

error in the weaker isotopologue intensities. Overall,

the target function represented by Equation 8

provided the best behaviour.

For each parameter optimization, GAIMS used a

linear annealing scheme over 1,000,000 steps.

Genetic algorithm settings included a population

size of 20 with a cross-over versus mutation rate

ratio of 1:20. Mutation steps changed three

parameters at a time to compensate for any

dependencies between parameters. Each

optimization was performed 50 times to verify

robustness (i.e. avoidance of local minima) and to

provide meaningful statistics of convergence.

2.4 Model Selection using AIC

We developed a model selection method using the

following form of the Akaike information criterion

or AIC (Akaike, 1974):



 ≈ 2 + log

∑



,



,















(9)

In Equation 9, k is the number of moiety model

parameters being optimized. The log of the average

sum of squares of differences approximates the log

likelihood of a given model. The calculated

isotopologue intensities I

i,calc

are derived from

average moiety model parameters for all 50

optimizations. With this equation, we can compare

models with a different number of optimizable

parameters. This model selection method was

developed as a part of GAIMS.

3 RESULTS

3.1 Fit of Expert-derived

Moiety Model

Figure 3 shows the fit of calculated isotopologue

intensities from the expert-derived moiety model

(Equations 7) to the 72-hour time point of

experimental isotopologue intensities representing

METABOLIC MODELING OF CONVERGING METABOLIC PATHWAYS - Analysis of Non-steady State Stable

Isotope-resolve Metabolism of UDP-GlcNAc and UDP-GalNAc

111

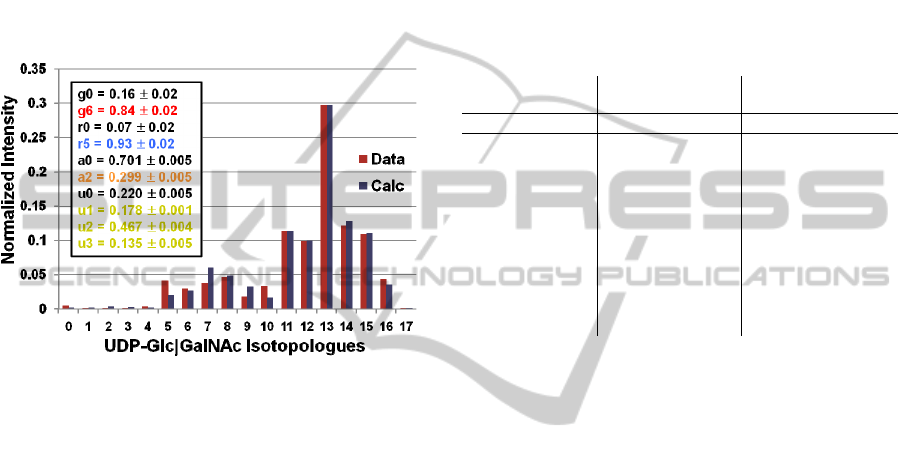
both UDP-GlcNAc and UDP-GalNAc. From this fit,

we obtain values for each functional moiety state

variable. All fifty optimizations converged quite

well as indicated by the standard deviations in state

variables. Interestingly, the fit of high intensity

isotopologues appears better than low intensity

isotopologues. In addition, we repeated this analysis

with 50 optimizations using 10,000,000 steps and 50

optimizations using 100,000 steps and obtained very

similar results in both parameter values and standard

deviations (data not shown), further demonstrating

the robustness of the parameter optimization.

Figure 3: Fit of optimized expert-derived moiety model to

FT-ICR-MS isotopologue data of UDP-GlcNAc and UDP-

GalNAc from tissue culture sample after 72 hours of

labeling with uniformly

C-labeled glucose.

3.2 Comparison of Models

using a Target Function

To explore reasons why some of the low intensity

isotopologues did not fit as well, we examined

alternative moiety models that tested assumptions of

our original model. From the pathway diagram in

Figure 2, there is the possibility that scrambling of

C incorporation in the acetyl moiety might be

occurring via amino acid biosynthetic and catabolic

pathways on the time-scale of 72 hours. So we

created an extended acetyl model with additional

terms (i.e., I

= g0r0a0u1 + g0r0a1u0) in Equations

7 using the acetyl moiety state variable a1 along

with the following relationship:

a0 + a1 + a2 = 1 (10)

In a similar manner, we created another

alternative moiety model with the addition of the u4

state variable for the uracil moiety. This CO

inclusive model tested the hypothesis that all CO

used in uracil biosynthesis is unlabeled. Likewise,

the relationship between uracil state variables was

expanded in the following manner:

u0 + u1 + u2 + u3 + u4 = 1 (11)

Table 1 shows the comparison between the three

moiety models. The value indicated for the target

function is the average across all 50 optimizations

for each model. Equation 8 clearly indicates that this

is a minimizing target function and thus lower

values are better.

Table 1: Comparison between three moiety models using

the average value of the target function.

-Inclusive

(7_G1R1A1U4)

Expert-Derived

(6_G1R1A1U3)

Extended Acetyl

(7_G1R1A2U3)

TF = 0.1103 TF = 0.1096 TF = 0.0913

g0 = 0.15

g6 = 0.85

r0 = 0.08

r5 = 0.92

a0 = 0.70

a2 = 0.30

u0 = 0.22

u1 = 0.18

u2 = 0.47

u3 = 0.14

u4 = 0.001

g0 = 0.16

g6 = 0.84

r0 = 0.07

r5 = 0.93

a0 = 0.70

a2 = 0.30

u0 = 0.22

u1 = 0.18

u2 = 0.47

u3 = 0.14

g0 = 0.15

g6 = 0.85

r0 = 0.08

r5 = 0.92

a0 = 0.28

a1 = 0.15

a2 = 0.57

u0 = 0.54

u1 = 0.15

u2 = 0.22

u3 = 0.09

The results in Table 1 clearly indicate that the

-inclusive model is worse than the expert-

derived model. Moreover, the extended acetyl model

appears to be the best model. However, the extended

acetyl model has one additional optimizable

parameter, which might afford the improvements

observed in the target function.

We also optimized an additional CO

-inclusive

model where the

C incorporation via CO

was

modelled as its own state variables c0 and c1. This

moiety model gave very similar results to those for

the original CO

-inclusive model, indicating that the

specific implementation of a model is not critical

(data not shown).

3.3 Comparison of Models using AIC

We used the form of the AIC in Equation 9 to

address the issue of model comparison involving

different number of optimizable parameters. The

AIC is calculated for each model using the average

parameter values across the 50 GAIMS

optimizations. But instead of just comparing three

possible models, we created a set of over 40 moiety

models to compare, ranging from plausible to

completely nonsense models. The expert-derived

model is represented by the identifier 6_G1R1A1U3,

where the first number indicates the number of

optimizable parameters in the model and

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

112

G1R1A1U3 represents one parameter in the glucose

moiety, one parameter in the ribose moiety, one

parameter in the acetyl moiety, and three parameters

in the uracil moiety, respectively. Deviations from

the expert-derived model are indicated by state

variables that are modified or added.

Table 2: Comparison of 40 moiety models using the AIC

and the experimental FT-ICR-MS isotopologue data of

UDP-GlcNAc and UDP-GalNAc at the 72-hour time

point.

AIC Moiety Model

-157.43

-109.64

-136.29

-154.32

-137.17

-133.12

-159.00

-72.52

-151.40

-153.52

-156.29

-158.25

-153.65

-159.24

-147.55

-163.39

-153.95

-153.64

-158.87

-151.21

-160.84

-154.17

-156.58

-158.22

-154.14

-159.10

-157.39

-148.47

-161.97

-153.91

-154.09

-158.85

-151.36

-159.52

-155.89

-154.77

-156.24

-152.79

-156.13

-155.50

6_G0R2A1U3_g3r2r3_g6r5

6_G1R1A1U3_a1

6_G1R1A1U3_g5

6_G1R1A1U3

6_G1R1A1U3_r4

6_G1R1A1U3_u4

7_G0R2A2U3_g3r2r3_g6r5

7_G0R3A1U3_g3r2r3_g6r5_g5r4

7_G0R3A1U3_g3r2r3_g6r5_r4

7_G1R1A1U3C1

7_G1R1A1U4

7_G1R1A2U3

7_G1R2A1U3_g3r2r3

7_G1R2A1U3_r1

7_G1R2A1U3_r2

7_G1R2A1U3_r3

7_G1R2A1U3_r4

7_G2R1A1U3_g1

7_G2R1A1U3_g2

7_G2R1A1U3_g3

7_G2R1A1U3_g4

7_G2R1A1U3_g5

8_G1R1A2U3C1

8_G1R2A2U3_g3r2r3_g6r5_g5

8_G1R2A2U3_g3r2r3

8_G1R2A2U3_r1

8_G1R2A2U3_r2

8_G1R2A2U3_r2r3

8_G1R2A2U3_r3

8_G1R2A2U3_r4

8_G2R1A2U3_g1

8_G2R1A2U3_g2

8_G2R1A2U3_g3

8_G2R1A2U3_g4

8_G2R1A2U3_g5

9_G2R2A2U3_r2r3_g1

9_G2R2A2U3_r2r3_g2

9_G2R2A2U3_r2r3_g3

9_G2R2A2U3_r2r3_g4

9_G2R2A2U3_r2r3_g5

9_G2R2A2U3_r2r3_g6r5_g3_g5

Table 2 shows the AIC for all these models

based on the 72-hour time point of experimental

isotopologue intensities. The models in red all

indicate AICs that are better than the expert-derived

model. However, the 7_G1R2A1U3_r4 model gave

the best (lowest) AIC even though this model with

ribose state variables r5, r4, and r0 makes no

biochemical sense given the known information

about the pentose phosphate pathway in human

cells. In fact, many nonsense models gave better

results than the expert-derived model, indicating a

significant problem with overfitting.

3.4 Model Selection using AIC

with Multiple Time Points

Table 3: Comparison of 40 moiety models using the AIC

and the experimental FT-ICR-MS isotopologue data of

UDP-GlcNAc and UDP-GalNAc at the 34-hour, 48-hour,

and 72-hour time points.

AIC Moiety Model

-321.81

-355.87

-326.98

-428.98

-332.69

-308.16

-291.31

-287.32

-290.16

-306.58

-293.12

-299.86

-294.52

-308.59

-288.94

-277.44

-244.47

-318.01

-317.89

-286.93

-277.12

-252.21

-288.84

-296.01

-288.88

-290.93

-296.67

-296.18

-251.87

-239.25

-303.97

-293.45

-288.32

-260.59

-236.42

-293.74

-279.33

-291.46

-241.63

-227.58

-276.84

6_G0R2A1U3_g3r2r3_g6r5

6_G1R1A1U3_a1

6_G1R1A1U3_g5

6_G1R1A1U3

6_G1R1A1U3_r4

6_G1R1A1U3_u4

7_G0R2A2U3_g3r2r3_g6r5

7_G0R3A1U3_g3r2r3_g6r5_g5r4

7_G0R3A1U3_g3r2r3_g6r5_r4

7_G1R1A1U3C1

7_G1R1A1U4

7_G1R1A2U3

7_G1R2A1U3_g3r2r3

7_G1R2A1U3_r1

7_G1R2A1U3_r2

7_G1R2A1U3_r3

7_G1R2A1U3_r4

7_G2R1A1U3_g1

7_G2R1A1U3_g2

7_G2R1A1U3_g3

7_G2R1A1U3_g4

7_G2R1A1U3_g5

8_G1R1A2U3C1

8_G1R2A2U3_g3r2r3_g6r5_g5

8_G1R2A2U3_g3r2r3

8_G1R2A2U3_r1

8_G1R2A2U3_r2

8_G1R2A2U3_r2r3

8_G1R2A2U3_r3

8_G1R2A2U3_r4

8_G2R1A2U3_g1

8_G2R1A2U3_g2

8_G2R1A2U3_g3

8_G2R1A2U3_g4

8_G2R1A2U3_g5

9_G2R2A2U3_r2r3_g1

9_G2R2A2U3_r2r3_g2

9_G2R2A2U3_r2r3_g3

9_G2R2A2U3_r2r3_g4

9_G2R2A2U3_r2r3_g5

9_G2R2A2U3_r2r3_g6r5_g3_g5

METABOLIC MODELING OF CONVERGING METABOLIC PATHWAYS - Analysis of Non-steady State Stable

Isotope-resolve Metabolism of UDP-GlcNAc and UDP-GalNAc

113

To address the issue of overfitting, we optimized

the isotopologue data for the 34-hour, 48-hour, and

72-hour time points simultaneously and calculated

an AIC for the combined optimization. The expert-

derived model had the best AIC of -428.98. The next

best model 6_G1R1A1U3_a1 was significantly

worse with an AIC of -355.87, indicating that

overall, the expert-derived model provides the best

description of the data.

4 CONCLUSIONS

We have demonstrated a novel metabolic modelling

methodology applied to FT-ICR-MS isotopologue

intensity data for UDP-GlcNAc and UDP-GalNAc.

Our implementation, GAIMS, interprets a set of

isotopologues as the flow of functional moieties

through metabolic pathways. This is represented by

a set of optimizable parameters for a given moiety

model. Figure 2 demonstrates a solid convergence of

50 individual optimizations for an expert-derived

model based on what is currently known about

UDP-GlcNAc biosynthesis. However, the standard

deviations for parameter values should not be

interpreted as a close representation of parameter

error, especially with the indication of model

overfitting in results from Table 2.

In addition, we demonstrate a robust model

selection method, which uses a form of the Akaike

information criterion (Equation 9). Our use of the

average parameter values from a set of optimizations

allows the AIC to sense smoothness of the error

surface for the target function of a given moiety

model. This application of the AIC along with the

use of isotopologues from multiple time points

enables our model selection method to overcome

issues of model overfitting for a set of isotopologues

at individual time points. We envision the coupling

of this robust model selection method with newer

non-steady-state metabolic flux analytical methods

(Selivanov et al., 2006; Wahl et al., 2008) as a

logical next step.

ACKNOWLEDGEMENTS

This work was supported in part by National Science

Foundation EPSCoR grant # EPS-0447479, NIH

NCRR Grant 5P20RR018733, 1R01CA118434-

01A2 (TWMF), 1RO1 CA101199 (TWMF)

R21CA133688-01 (ANL) from the National Cancer

Institute, DOE Grant Number DE-EM0000197

(HNBM), the Cardinal Research Cluster, the

Kentucky Challenge for Excellence, and the Brown

Foundation.

REFERENCES

Akaike, H., 1974. “A new look at the statistical model

identification”, IEEE Transactions on Automatic

Control, 19, 716–723.

Edwards, J. S., Ibarra, R. U., Palsson, B. O., 2001. “In

silico predictions of Escherichia coli metabolic

capabilities are consistent with experimental data”,

Nature Biotech, 19, 125-130.

Fell, D. A., 1984. “Fat synthesis in adipose tissue. An

examination of stoichiometric constraints”, J Biochem,

238, 781-786.

Fell, D.A., 1997. Understanding the Control of

Metabolism, London: Portland Press.

Gambetta, M. C., Oktaba, K., & Müller, J., 2009.

“Essential Role of the Glycosyltransferase Sxc/Ogt in

Polycomb Repression”, Science, 325, 93-96.

Harrigan, G. G., Goodacre, R. (Ed), 2003. Metabolic

profiling: its role in biomarker discovery and gene

function analysis, Boston: Kluwer Academic

Publishers.

Hart G. W., Housley M. P., Slawson C., 2007. "Cycling of

O-linked beta-N-acetylglucosamine on

nucleocytoplasmic proteins", Nature, 446, 1017-1022.

Hellerstein, M. K., 2003. “In vivo measurement of fluxes

through metabolic pathways: the missing link in

functional genomics and pharmaceutical research”,

Annu Rev Nutr, 23, 379-402.

Kauffman, K. J., Prakash, P., Edwards, J. S., 2003.

“Advances in flux balance analysis”, Curr Opin

Biotech, 14, 491-496.

Lane A. N., Fan T. W-M., Higashi R. M., 2008.

“Isotopomer-based metabolomic analysis by NMR and

mass spectrometry". Methods in Cell Biology,Vol 84.

Biophysical Tools for Biologists, Vol 1,ed. Correia JJ,

Detrich HW. Elsevier Science & Technology Books

Ch.18. 541-588.

Lane, A. N., Fan, T. W-M., Xie, Z., Moseley, H. N. B.,

Higashi, R. M., 2009. “Stable isotope analysis of lipid

biosynthesis by high resolution mass spectrometry and

NMR.”, Anal Chim Acta, 651, 201-208.

Moseley, H. N. B., 2010. “Correcting for the Effects of

Natural Abundance in Stable Isotope Resolved

Metabolomics Experiments Involving Ultra-High

Resolution Mass Spectrometry”, BMC Bioinformatics,

11, 139-144.

Savinell, J. M., Palsson, B. O., “Optimal selection of

metabolic fluxes for in vivo measurement. I.

Development of mathematical methods”, J Theor Biol,

155, 201-214.

Sauer, U., Lasko, D. R., Fiaux, J., Hochuli, M., Glaser, R.,

Szyperski, T., Wuthrich, K., Bailey, J. E., 1999.

“Metabolic Flux Ratio Analysis of Genetic and

Environmental Modulations of Escherichia coli

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

114

Central Carbon Metabolism”, J Bacteriol, 181, 6679-

6688.

Sauer, U., 2006. “Metabolic networks in motion: 13C-

based flux analysis”, Mol Syst Biol, 2, 62.

Schellenberger, J., Palsson, B. O., 2009. “Use of

Randomized Sampling for Analysis of Metabolic

Networks”, J Biol Chem, 284, 5457-5461.

Selivanov, V. A., Marin, S., Lee, P. W. N., Cascante, M.,

2006. “Software for dynamic analysis of tracer-based

metabolomics data: estimation of metabolic fluxes and

their statistical analysis”, Bioinformatics, 22, 2806-

2812.

Stephanopoulos, G., “Metabolic fluxes and metabolic

engineering”, Metab Eng, 1, 1-11.

Wahl, S. A., Nöh, K., Wiechert, W., 2008. “13C labelling

experiments at metabolic nonstationary conditions: An

exploratory study”, BMC Bioinformatics, 9, 152-169.

METABOLIC MODELING OF CONVERGING METABOLIC PATHWAYS - Analysis of Non-steady State Stable

Isotope-resolve Metabolism of UDP-GlcNAc and UDP-GalNAc

115