MODELING DELAYS IN STATE TRANSITION OF A BISTABLE
GENETIC SWITCH UNDER THE INFLUENCE OF EXTRINSIC
NOISE
Jaroslav Albert and Marianne Rooman
BioSystems, BioModeling and Bioprocesses, Universit´e Libre de Bruxelles
CP 165/61 avenue Roosevelt 50, 1050 Bruxelles, Belgium
Keywords:
Bistable genetic switches, Delays, Modeling gene expression, Moise, Robustness.
Abstract:
Among other functions, bistable genetic switches serve as decision-makers, accepting or rejecting noisy input
signals. In some instances, e. g. during developmental stages, it is imperative that, once an input signal is
accepted, the gene’s expression remains virtually unchanged for a certain period of time before evolving to
its other stationary state. In this paper, we aim to tackle the question of what causes this delay to occur. We
look at a particular model of a bistable switch and study the conditions which lead to delayed state transitions.
Given that every biological system is subject to noise, it is imperative that any model capable of explaining
and predicting these delays is robust against random parameter perturbations. Therefore, in order to test the
robustness of the model, we subject the system to random noise and show that for particular combinations of
parameter values, its effects on the delays are negligible. It is demonstrated that the ratio of protein to mRNA
degradation rates plays a critical role in the system’s confidence to generate accurate delays.
1 INTRODUCTION
For a long time, bistable switches have been the focus
of extensive research in both experimental and theo-
retical domains ((Griffith (1968); Kauffman (1975);
Watson (1976); Meinhardt and Gierer (1980); Cherry
and Adler (2000); Gardner et al. (2000))). One area
of study has focused on the ability of switches to dis-
tinguish important input signals from random noise
((Fritz et al. (2007))), while in other studies noise
was shown to play a positive role in regulating gene
expression and amplification of protein production
((Hasty et al. (2000))) and inducing state transitions
((Horsthemke and Lefever (1984))). Although a lot
of progress has been made towards understanding the
dynamics of bistable switches in noisy environments
and the conditions under which they can reliably op-
erate ((Guantes and Poyatos (2008))), much less at-
tention has been payed to the ability of some switches
to delay their transition from one stationary state to
another. In this paper, we aim to explore this phe-
nomenon.
First, we examine the properties of a bistable
switch in terms of an analogy to a particle, moving
in one-dimensional potential while being resisted by
a frictional force. The shape of the potential, which is
a function of only two effective model parameters, is
shown to be the only factor in determining whether or
not switching occurs. Next, we model the dynamics
of the switch in the presence of noise, acting on the
model parameters, and study its effects on delays. Fi-
nally, the most suitable conditions, i. e. the range of
parameter values, for inducing delays under the influ-
ence of noise are discussed.
2 MODEL STRUCTURE OF A
BISTABLE SWITCH
Us and ((Trotta et al. (2010))) have independently an-
alyzed the mechanism of delayed switching based on
the Griffith model discussed below. Here, we briefly
summarize our analysis.
The evolution of a bistable switch can be captured
by the following set of differential equations first pro-
posed by Griffith ((Griffith (1968))):
˙x = r
(γy)
2
1+ (γy)
2
− k
x
x+ r
0
, (1)
˙y = Kx− k
y
y, (2)
where x and y are the mRNA and protein concen-
278
Albert J. and Rooman M..
MODELING DELAYS IN STATE TRANSITION OF A BISTABLE GENETIC SWITCH UNDER THE INFLUENCE OF EXTRINSIC NOISE.
DOI: 10.5220/0003133402780282
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 278-282
ISBN: 978-989-8425-36-2
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

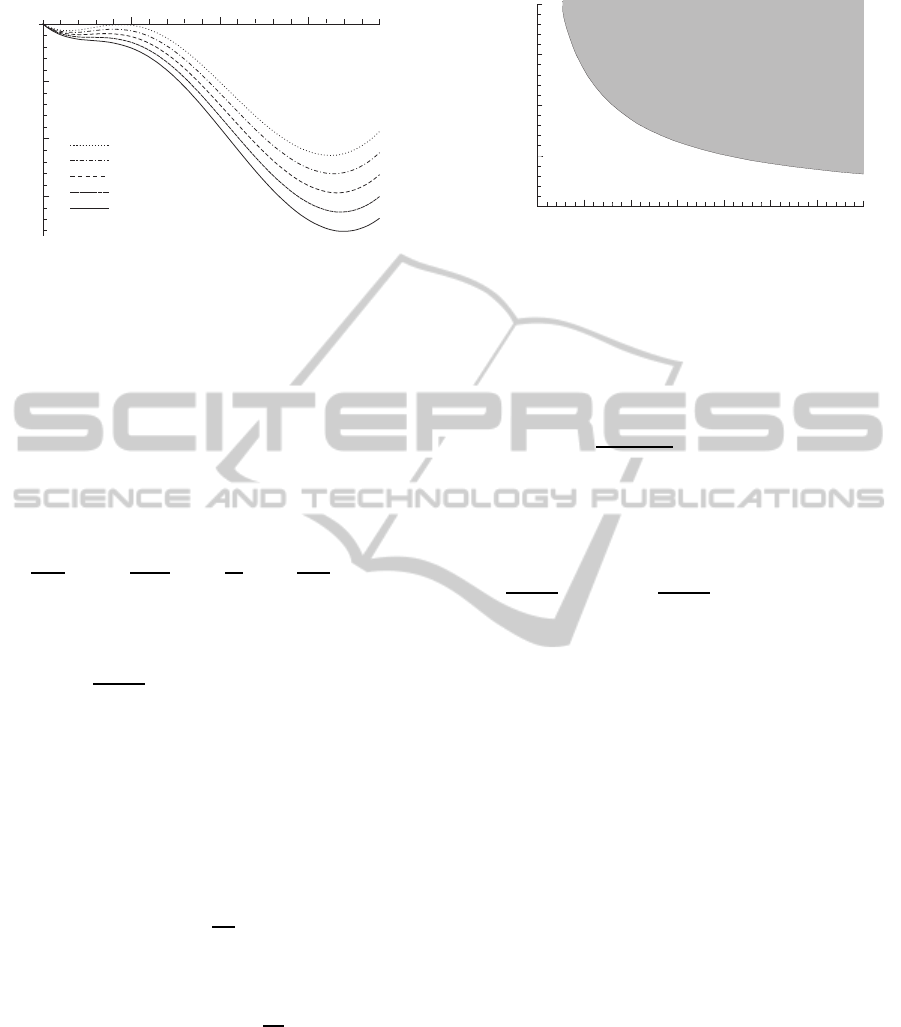
-0.05
-0.10
-0.15
0.5
1.0
1.5
a = 0.10
0
a = 0.11
0
a = 0.12
0
a = 0.13
0
a = 0.14
0
V()
h
h
Figure 1: Potential curves corresponding toα
0
= 0.10, 0.11,
0.12, 0.13, 0.14 and α = 2.1.
tration levels respectively. In respective order, the
model parameters in Eq. (1), r, γ, k
x
and r
0
, stand
for the maximum transcription rate, the inverse dis-
sociation factor, degradation rate of mRNA, and the
minimum or basal transcription rate. In Eq. (2), K is
the rate of translation while k
y
is the degradation rate
of the translated protein. For simplicity, we redefine
all quantities in Eqs. (1) and (2) as follows:
α ≡
Kγr
k
x
k
y
, α
0
≡
Kγr
0
k
x
k
y
, β ≡
k
y
k
x
, ξ ≡
Kγx
k
y
, η ≡ γy.
(3)
This leads to a set of equations with fewer parameters:
˙
ξ = α
η
2
1+ η
2
− ξ+ α
0
,
˙
η = β(ξ − η), (4)
where the dot denotes derivative with respect to τ =
k
x
t.
In order to get a sense for the model structure and
its implications on the system dynamics, we first dif-
ferentiate Eq. (2), and then, solving algebraicly for
˙
ξ
and ξ in terms of
˙
η and η, write a second order differ-
ential equation entirely in terms of η as
¨
η = −ν
˙
η−
∂
∂η
V(η), (5)
where
V(η) = −β

α(η− tan
−1
η) −
η
2
2
+ α
0
η

, (6)
and ν = 1+ β. Equation (5) describes a particle acted
on by two forces: −∂V(η)/∂η and a frictional force
ν
˙
η. Since β in Eq. (6) is merely a multiplicative fac-
tor, it plays no role in determining the shape of the
potential. Figure 1 shows the shape of V(η) as a func-
tion of α and α
0
.
With rising α
0
, the potential barrier between the
two minima decreases and disappears completely
0.05
0.10
0.15
0.20
0.00
1 2
3
4 6 7 8
a
a
0
5
Geneoff
Geneon
Figure 2: A section of the parameter space (α, α
0
). Any
combination of parameters which falls onto the shaded re-
gion guarantees gene activation. For a fixed value of β, each
point in this region corresponds to a particular delay.
when the first local minimum and maximum converge
into a zero inflection point: ∂
2
V(η)/∂η
2
= 0 or
2αη
(1+ η
2
)
2
− 1 = 0. (7)
If we let η
0
denote the first real solution to this equa-
tion, then the necessary condition for a transition to
the global minimum becomes
∂V(η)
∂η




η=η
0
= −α
η
2
0
1+ η
2
0
+ η
0
− α
0
< 0. (8)
Figure 2 shows the region in parameter space that al-
lows this transition to occur. Since α and α
0
together
contain all the other model parameters, the condition
expressed in Eq. (8) can provide biologically relevant
information about the state of the genetic switch.
The time it takes the system to evolve from one
minimum to the other depends on the slope at the in-
flection point η
0
and the coefficient of friction ν. The
less negative this slope and the larger ν, the longer
it takes to make this transition. By selecting values
for the model parameters, one can set the gene, much
like an alarm clock, to become activated after a de-
sired time.
3 DELAYED STATE
TRANSITIONS IN THE
PRESENCE OF NOISE
Noise is an unavoidable part of all biological systems.
Hence, only those models that can reproduce a sys-
tem’s behavior under noisy conditions can be said to
have any biological significance. We distinguish be-
tween two types of noise: intrinsic and extrinsic.
MODELING DELAYS IN STATE TRANSITION OF A BISTABLE GENETIC SWITCH UNDER THE INFLUENCE OF
EXTRINSIC NOISE
279

3.1 Intrinsic Versus Extrinsic Noise
Intrinsic noise comes about as a consequence of ran-
dom collisions among DNA, RNAs, proteins, and
small molecules within the cell ((Hasty et al. (2000))).
In small systems, i. e. systems with low concen-
tration levels of mRNA and Protein, and small cell
volumes, these collisions cause the concentration lev-
els to fluctuate with frequencies comparable to the
macroscopic rates of transcription, translation, and
degradation (see (Koern et al. (2005)) for a review).
In the opposite limit however, the system dynamics
tend towards the deterministicly predicted behavior
as, for example, described by differential equations
((Kampen (1992))).
Extrinsic noise arises from slow (compared to
typical collision frequencies) fluctuations of one or
more of the macroscopic parameters as a response to
changes in the chemical environment ((Hasty et al.
(2001))). As an example, one can consider a postrans-
lational modification of a particular protein, causing
its degradation rate to change ((Guantes and Poyatos
(2008); ?)). The specific molecules responsible for
this modification will fluctuate in concentration due
to macroscopic effects such as spacial inhomogene-
ity and cell division, and will modify the differential
equations through an addition of a random function
added to the protein degradation rate. Similar argu-
ments can be applied to all other parameters.
3.2 Effects of Extrinsic Noise on Time
Delays
We model the effects of extrinsic noise on time de-
lays by multiplying one model parameter at a time
by a stochastic term 1 + δ(τ), where δ(τ) is a piece-
wise continuous function whose value changes ac-
cording to a Gassian distribution with variance σ
2
n
.
The changes in δ(τ) are separated by time intervals
whose values are assigned probabilistically according
to the Poisson distribution. This function is analogous
the one representing the velocity of a Brownian parti-
cle moving along one-dimension.
Without an external input, i. e. a chemi-
cal acting on one of the parameters, α and α
0
are
set to 2.1 and 0.1 respectively for five cases of β:
0.1,0.3,0.5,0.7,0.9. The exact combination of the
parameter values for r, γ, k
x
, r
0
, K, and k
y
is irrel-
evant as long as the chosen values of α, α
0
and β
are respected. For the parameter that is varied - here
called the control parameter - twentyfive combina-
tions of noise variance σ
2
n
and frequency f are cho-
sen, corresponding to σ
n
= 0.05,0.1,0.15,0.2,0.25
and f
−1
= 0.02,0.04,0.06,0.08,0.1. Twelve values
.
.
.
.
.
.
.
.
.
.
.
.
40
60
80
100
120
140
160
60
80
100
120
140
160
40
Delaywithoutnoise
Delaywithnoise
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
40
60
80
100
120
140
160
60
80
100
120
140
160
40
Delaywithoutnoise
Delaywithnoise
.
.
.
.
.
.
.
.
.
.
.
.
a)
b)
Figure 3: Exact delays d
Ex
versus the average delays d
Av
for k
y
as the control parameter subject to noise with σ
n
=
0.15, f
−1
= 0.04. In a) β = 0.1 and b) β = 0.7. The total
variance σ
L
+ σ
R
for each delay shown in the two figures
demonstrates the importance of β on the delays.
are selected for each control parameter in such a way
that, in the absence of noise, the delays range from
40 to 150 (in arbitrary units) by steps of ten. For
every one of the twelve values of a control parame-
ter, we compute the delay d thirty times, and record
their average d
Av
. The left (right) standard deviation
σ
L
(σ
R
), which corresponds to all points satisfying
d < d
Av
(d > d
Av
) is also computed. Figure 3 illus-
trates the comparison between the delays in the pres-
ence versus the absence of noise for two values of β.
To have a quantitative measure of how well the de-
lays of the stochastic system match up with the exact
delays, we define
Q =
s

σ
L
+ σ
R
d
Av

2
+

d
Av
− d
Ex
d
Ex

2
, (9)
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
280

where d
Ex
stands for the exact delay in the absence of
noise. The bar charts in figures 4 a, b, and c show
the values of Q for all parameters (see figure cap-
tions) and for three different delays, d
Ex
= 40, 10,15,
respectively.
0.05
0.10
0.15
0.20
0.25
0.30
0.1
0.2
0.3
0.4
0.5
0.6
0.2
0.4
0.6
0.8
Q
Q
Q
a)
c)
b)
Figure 4: Bar charts showing Q along the vertical axis for
three different delays: a) d
Ex
= 40, b) d
Ex
= 100, and c)
d
Ex
= 150. Each shade of gray represents one parameter in
the order (left to right) r, r
0
, k
x
, γ, K, and k
y
. Within each
shade, the columns correspond to the five values of β: 0.1,
0.3, 0.5, 0.7, 0.9.
4 CONCLUSIONS
We have studied the effects of extrinsic noise on the
activation delays of a genetic switch. Our analysis
shows that, although any of the parameters in the
model can be manipulated to generate delays, not all
parameters are equally robust against external noise.
In particular,looking at theaverage
¯
Q =
∑
β
Q for each
parameter, one finds that K, the translation rate, is
most suseptible to external noise and therefore least
suitable for generating delays. On the other hand, r
and r
0
, having the lowest
¯
Q among all parameters, can
be used to induce delays with the highest confidence.
Two observations should be made: first, the above
results indicate that all parameters gain robustness
with decreasing β; and second, Q falls as the de-
lays increase. Therefore, knowing β for a partic-
ular gene, one can estimate the likelyhood of that
gene to play a role in generating delays. In most
cases, β is always less than 1 ((Hargrove and Schmidt
(1989))) and can be as small as 0.007 ((Yamamoto
et al. (1988))). However, for some proteins and their
corresponding mRNA’s, such as the Glucocorticoid
receptor ((Rosewicz et al. (1988))) and Ornithine de-
carboxylase ((Rogers et al. (1986))), it can range from
1 up to 4. Although in the deterministic case the de-
lays can reach infinity, in the presence of noise Q in-
creases as a function of d
Ex
, which suggests a limit on
the length of time the switch can be reliably delayed.
As a final comment, we point out that some mod-
els of the genetic switch neglect the translational time
lapse between the synthesis of mRNA and the cor-
responding protein. Under this assumption the two
quantities ξ and η in Eqs. (4) can be equated, which
leads to a single equation for ξ. Mathematically, this
simplification can be justified only for β ≫ 1. As this
limit is unrealistic for most biological systems, one
may conclude that in the context of delayed switch-
ing, Eqs. (4) constitute the minimal model required
to explain long time activation delays.
ACKNOWLEDGEMENTS
We thank L. Trotta, E. Bullinger, M. Kinnaert and T.
Konopka for useful discussions.
REFERENCES
J. S Griffith, J. theor. Biol. vol. 20, no. 2, pp. 65-88 (1968)
S. Kauffman, Ciba Foundation Symp. vol. 29, p. 201
(1975), Amsterdam: Elsevier.
J. D. Watson, Molecular Biology of the Gene W. A. Ben-
jamin, Inc.(1976) Manlo Park
H. Meinhardt,A. Gierer, J. theor. Biol. vol. 85, p. 429-450
(1980)
J. L. Cherry, F. R. Adler, J. theor. Biol. vol. 203, p. 117-133
(2000)
T. S. Gardner, C. R. Cantor, J. J. Collins, Nature vol. 403,
p. 339-342 (2000)
G. Fritz, N. E. Buchler, T. Hwa, U. Gerland, Syst. Synth.
Biol. vol. 1, p. 89-98 (2007)
J. Hasty, J. Pradines, M. Dolnik, J. J. Collins, PNAS vol.
97, no. 5, p. 2075-2080 (2000)
MODELING DELAYS IN STATE TRANSITION OF A BISTABLE GENETIC SWITCH UNDER THE INFLUENCE OF
EXTRINSIC NOISE
281

W. Horsthemke, R. Lefever, Noise-Induced Transitions
Springer-Verlag (1984) Berlin
R. Guantes, J. F. Poyatos, PLOS Comp. Biol. vol. 4, Issue
11, e1000235 (2008)
L. Trotta, R. Sepulchre, E. Bullinger, accepted to the 2010
IEEE Conference on Decision and Control (2010)
M. Koern, T. C. Elston, W.j. Blake, J.J. Collins, Nature
Reviews vol. 6, p. 451-464 (2005)
N. G. vanKampen, Stochastic Processes in Physics and
Chemistry North-Holland Personal Library, (1992)
Amsterdam
J. Hasty, F. Isaacs, M. Dolnik, D. McMillen, J. J. Collins,
Chaos vol. 11, p. 207-220 (2001)
J. Wang, J. Zhanf, Z. Yuan, T. Zhuo, BMC Systems Biology
vol. 1, p. 50 (2007)
J. L. Hargrove, F. H. Schmidt, The FASEB Journal vol. 3,
p. 2360-2370 (1989)
M. Yamamoto, S. Kure, J. D. Engel, K. Hiraga, J. Biol.
Chem. vol. 263, p. 15973-15979 (1988)
S. Rosewicz, A. R. McDonald, B. A. Maddux, I. D.
Goldfine, R. L. Miesfeld, C. D. Lugsdon J. Biol.
Chem. vol. 263, p. 2581-2584 (1988)
S. Rogers, R. Wells, M. Rechsteiner, Science vol. 234, p.
364-368 (1986)
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
282