OPTIMAL SAMPLE SELECTION FOR BATCH-MODE

REINFORCEMENT LEARNING

Emmanuel Rachelson, Franc¸ois Schnitzler, Louis Wehenkel and Damien Ernst

Monteﬁore Institute, University of Li

ege, B-4000 Li

ege, Belgium

Keywords:

Stochastic optimal control, Sample control, Reinforcement learning.

Abstract:

We introduce the Optimal Sample Selection (OSS) meta-algorithm for solving discrete-time Optimal Control

problems. This meta-algorithm maps the problem of ﬁnding a near-optimal closed-loop policy to the iden-

tiﬁcation of a small set of one-step system transitions, leading to high-quality policies when used as input

of a batch-mode Reinforcement Learning (RL) algorithm. We detail a particular instance of this OSS meta-

algorithm that uses tree-based Fitted Q-Iteration as a batch-mode RL algorithm and Cross Entropy search as a

method for navigating efﬁciently in the space of sample sets. The results show that this particular instance of

OSS algorithms is able to identify rapidly small sample sets leading to high-quality policies.

1 INTRODUCTION

Many problems in the ﬁelds of Finance, Engineer-

ing or Medicine can be cast as discrete-time Optimal

Control problems. Such problems feature a dynamic

system that evolves over several time steps and re-

ceives various rewards along the way, depending on

how well it performs. Solving these problems con-

sists in generating a sequence of appropriate control

inputs, in order for the system to follow a trajectory

providing an optimal cumulated reward. In the gen-

eral case, this resolution rapidly becomes very chal-

lenging as the problem’s size grows. Optimal Control

problems have been studied by various communities

(e.g., Artiﬁcial Intelligence, Control Systems, Opera-

tions Research, or Machine Learning), each using dif-

ferent assumptions and formalisms to design algorith-

mic solutions.

Reinforcement Learning (RL) (Sutton and Barto,

1998) is a subﬁeld of Machine Learning where one

tries to infer a good closed-loop control policy from

the sole knowledge of an observed set of one-step sys-

tem transitions and their associated rewards. Such a

set results from the sampling of the system’s under-

lying dynamics and rewards. When this set of sam-

ples is given at once, as an input of the learning al-

gorithm, one talks of batch-mode RL. In recent years,

batch-mode RL algorithms, such as the tree-based Fit-

ted Q-Iteration (FQI) (Ernst et al., 2005) or the Least

Squares Policy Iteration (Lagoudakis and Parr, 2003a)

algorithms, proved successful in tackling large Opti-

mal Control problems. These methods relied on ap-

propriate approximation architectures to efﬁciently

generalize information throughout the state space. We

now wish to understand how they could be used for

solving large-scale problems when one has some free-

dom in the sample set input. In other words, we break

free from the standard batch-mode RL hypothesis of

a ﬁxed, imposed sample set, and suppose that a gen-

erative model is available, providing an unconstrained

way of picking new sample sets. Suppressing the con-

straint of a ﬁxed, unquestionable input sample set,

and allowing this input to be considered as a prob-

lem’s variable, raises the question of identifying a set

of one-step transitions which maximizes the learning

algorithm’s output, while keeping the number of such

one-step transitions low, so as to extract good policies

from the sample set in a reasonable amount of time.

An immediate approach at answering this question

would be to collect experience uniformly and exten-

sively over the problem’s state-action space, as ﬁnely

as necessary to provide a good representation of the

system. But for large scale problems, as the dimen-

sion of this state-action space grows, such a sample

set becomes so large that processing it becomes in-

creasingly difﬁcult (as reported in (Ernst, 2005) for

instance). Hence, the problem we address in this con-

text consists in identifying a training set of one-step

transitions which both has a limited size, and max-

imizes the algorithm’s output. For this purpose, we

concentrate on the question of ﬁnding the input sam-

ple set of size N that will generate the best possible

Rachelson E., Schnitzler F., Wehenkel L. and Ernst D..

OPTIMAL SAMPLE SELECTION FOR BATCH-MODE REINFORCEMENT LEARNING.

DOI: 10.5220/0003133500410050

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 41-50

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

output policy, for a given batch-mode RL algorithm

and a predeﬁned sample set size N.

After recalling, in Section 2, the main notions

of discrete-time Optimal Control and Reinforcement

Learning, we formulate the search for an optimal

ﬁxed-size sample set as an optimization problem and

discuss its properties in Section 3. This leads to the

deﬁnition of the general Optimal Sample Selection

(OSS) meta-algorithm for solving Optimal Control

problems. Section 4 details a particular instance of

OSS, using the tree-based FQI algorithm and Cross-

Entropy search. Section 5 reports the method’s re-

sults on the “car on the hill” domain, empirically il-

lustrating the fact that small optimized sample sets

can lead to high quality policies. Building on these

optimization results, Section 6 discusses some more

general properties of OSS methods, highlighting their

strengths, weaknesses and perspectives. We particu-

larly emphasize their potential for solving large scale

Optimal Control problems. We ﬁnally summarize our

contribution and conclude in Section 7.

2 OPTIMAL CONTROL AND

REINFORCEMENT LEARNING

The framework of discrete-time Optimal Control

(Bertsekas and Shreve, 1996) covers decision prob-

lems where one tries to control a system, character-

ized by its state x ∈ X, through the application of a

sequence of discrete-time commands (u

)

t∈N

∈U,

in order to optimize a criterion based on the system’s

trajectory. Formally, such problems are described by

a four-tuple hX ,U, f ,ri, where X is the state space in

which the system evolves, U is the set of all possi-

ble commands (or actions), f and r are respectively a

transition and a reward model as illustrated on Figure

1. In the deterministic case, at time step t, if command

u is applied while the system is in state x, a transition

is triggered to the next state x

= f (x, u). For this tran-

sition, a reward r(x, u) is gained.

In the general case of stochastic Optimal Control,

the (stationary) transition model is actually stochas-

tic: f (x, u) is a distribution over the possible next

states x

, and one writes x

∼ f (x,u). The reward func-

tion then corresponds to the expected one-step reward

for the considered state-action pair. For the sake of

simplicity, we will consider deterministic problems in

Sections 3 to 5 and will extend our approach to the

stochastic case in Section 6.

A (stationary) closed-loop controller, or decision

policy, for a discrete-time Optimal Control problem

is a function µ : X →U (µ ∈ F (X,U)), mapping each

state x to an action u to undertake. The criterion J

t + 1

′

= f (x, u)

r(x, u)

reward:

state:

time:

Figure 1: Transition and reward models of a discrete-time

control problem.

will consider in order to discriminate between policies

and deﬁne optimality is the standard, inﬁnite horizon,

γ-discounted criterion. It maps each state x to the sum

of the γ-discounted successive rewards obtained when

applying policy µ from x, for an inﬁnite number of

steps: ∀x ∈X,

(x) =

∞

∑

t=0

r(x

,µ(x

)) with



= x and

t+1

= f (x

,µ(x

))

Then, a policy µ

∗

is said to be optimal if:

∀x ∈ X ,µ ∈ F (X,U), J

∗

(x) ≥ J

(x)

The J

function of a policy µ is called its value

function. One writes J

∗

the value function of any op-

timal policy.

RL algorithms aim at ﬁnding the best control pol-

icy when the transition and reward models of the pro-

cess are unknown. Instead, they rely on the collec-

tion of one-step transition samples from this under-

lying model. Each sample describes a one-step tran-

sition as a four-tuple (x, u,r, x

). These samples can

be obtained either from interaction with the physical

system or from a generative model. Hence, the stan-

dard input of any batch-mode RL algorithm is a set

of samples D = {(x,u,r,x

)}, approximating the tran-

sition and reward models, from which the algorithm

infers a policy µ

∗

Since many applications of RL have very large

or multi-dimensional, continuous state spaces, ﬁnd-

ing an exact representation of the optimal policy or

value function is often a very difﬁcult task. Conse-

quently, there is a need for approximation methods

that are able to solve the policy inference problem in

a compact and efﬁcient fashion (Bus¸oniu et al., 2010).

In order to overcome this difﬁculty, different value

function and policy approximation architectures have

been proposed in the literature, such as combinations

of linear features (Boyan, 1999), kernel methods (Or-

moneit and Sen, 2002), forests of trees (Ernst et al.,

2005) or classiﬁers (Lagoudakis and Parr, 2003b). All

these methods have greatly contributed to extending

the practical applicability of RL.

3 OPTIMIZING SAMPLE SETS

The general goal of batch-mode RL is, given a sam-

ple set D as input, to compute a policy µ

∗

which is as

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

sample(·)

policy inference(·)

∗

score(·)

M (θ)

Figure 2: Score of a sampling scheme.

close as possible to an optimal policy for the system

the samples were gathered from. The RL literature

provides a whole span of efﬁcient methods to com-

pute such a µ

∗

Consider the context where a generative model of

the system is available. Such a model outputs a one-

step transition (x,u, r,x

) when presented with a state x

and an action u. In many Optimal Control problems,

such a model is often available. Since we have this

generative model, the input sample set D is no longer

imposed to us. The Optimal Control practitioner will-

ing to exploit batch-mode RL methods then needs to

answer the simple question of how to generate a good

sample set, prior to running his favourite algorithm.

The generic question of collecting data for batch-

mode RL algorithms has received little attention in

the literature, as this problem is usually tackled from

a problem-speciﬁc point of view (e.g., (Neumann and

Peters, 2009; Riedmiller, 2005; Ernst et al., 2006)).

We investigate a way to tackle this problem from a

generic, problem-independent, point of view.

3.1 Optimal Sample Selection

We consider the framework where the sample set’s

size is ﬁxed and the batch-mode RL algorithm is

chosen, and, in this context, we introduce a meta-

algorithm

for generating good sample sets D.

Consider a sample set D =

{

(x,u, r,x

)

}

and let us

introduce the set θ =

{

(x,u)

}

which we call the sam-

pling scheme leading to D. Although, in the determin-

istic case, there is a complete equivalence between θ

and D, this distinction will appear necessary when we

extend this contribution to stochastic systems in Sec-

tion 6. Suppose also that, for convenience, we ordered

the different elements

in D and θ:

D =





i∈[1;N]

θ =

{

)

}

i∈[1;N]

Let sample(·) be the operator that computes D

from θ, using the generative model. Let also

policy inference(·) denote the batch-mode RL algo-

rithm used, taking a set D as input, and outputting a

We refer to it as “meta” because it considers a generic

batch-mode RL algorithm among its inputs.

For the sake of simplicity, in the remainder of the pa-

per, we will make a slight notation abuse and will refer to θ

indifferently as the set

{

(x,u)

}

or as the vector of variables

describing the elements of this set.

policy µ

∗

, which is optimal (or quasi-optimal) with

respect to an implicit, approximate problem, implied

by D. Let us ﬁnally assume there exists a generic cri-

terion score(µ), allowing to evaluate the actual quality

of a policy µ, when applied to the domain at hand.

Then we propose to identify a good training set by

formulating the following optimization problem (il-

lustrated on Fig 2):

∗

∈ argmax

θ∈(X×U)

M(θ) (1)

M(θ) = (score ◦policy inference ◦sample) (θ)

Hence, given an Optimal Control problem’s gen-

erative model, a batch-mode RL algorithm, and a size

N of sample sets, we call Optimal Sample Selection

method of parameter N (OSS(N)), an optimization

method searching for this optimal sampling scheme

∗

and returning µ

∗

= policy inference(sample(θ

∗

)),

as shown in Algorithm 1.

Algorithm 1: General layout of the OSS (N) meta-

algorithm.

Input: Batch-mode RL alg. policy inference(·), ;

Policy evaluation method score(·),;

Generative model sample(·).;

Deﬁne M(θ) as in Equation (1). ;

Compute θ

∗

= argmax

M(θ). ;

Return policy inference(sample(θ

∗

)).

3.2 Creating Instances of OSS(N)

The performance and behaviour of an OSS(N) in-

stance will depend on the choices made for score(·)

and policy inference(·), but also on the value of N

and on the optimization method used to solve prob-

lem 1. We provide hereafter some elements that may

help make these choices.

Score Function. The score function should be cho-

sen in order to guarantee that a policy which max-

imises this score is indeed a policy which, when used

to control the real system, leads to high cumulated re-

wards. If the initial states from which the policy will

have to drive the real system are known, a suitable

choice for the score(·) function could be for exam-

ple the average return of the policy over these initial

states. These returns can be evaluated through Monte-

Carlo simulations, using the generative model.

Batch-mode RL Algorithm. Most efﬁcient batch-

mode RL algorithms rely on value function or policy

approximation architectures. A necessary condition

for the OSS algorithm to work well is that there must

OPTIMAL SAMPLE SELECTION FOR BATCH-MODE REINFORCEMENT LEARNING

exist a sampling scheme leading to high-performance

policies, which implies that these architectures need

to be able to represent accurately (at least) the optimal

policy. In general, this necessary condition is more

likely to be veriﬁed if the RL algorithm relies on a

rich, versatile approximation architecture. Note also

that from one RL algorithm / approximation method

to the other, the optimal sampling scheme θ

∗

might

vary.

Choosing N. Picking N is a compromise between

policy quality and computation time. Larger N in-

crease the chance to ﬁnd good policies, since the do-

main dynamics are captured more ﬁnely, but also re-

sult in increased computation burden. As Section

4 will illustrate, the main source of complexity of

ﬁnding an optimal θ comes from the dependency of

policy inference(·)’s complexity on N. Hence, look-

ing for very small sample sets seems desirable. On the

other hand, below a certain threshold on N, the search

space (X ×U)

might not contain any element able to

generate a policy leading to an optimal score. When

N increases, there may exist more and more elements

in this search space that lead to policies having near-

optimal scores, and hence, ﬁnding such elements in

the resolution of problem 1 can be easier. Therefore,

the choice of N needs to balance the need for ﬁne do-

mains representation with the processing abilities of

policy inference(·). In very large domains, the former

constraint will prevail.

Optimization Algorithm. Computing or evaluat-

ing the gradient

∂M

∂θ

, or any subgradient of M(·) may

reveal itself very difﬁcult in the general case. In

some very speciﬁc cases of RL algorithms, approx-

imation architectures, and criteria used for M, an an-

alytic formulation might be found, but we concen-

trate on the general case where such a gradient is

not available. As a matter of consequence, we need

to carefully choose the optimization method we will

use in order to ﬁnd θ

∗

. Since we cannot use any

derivative of the M function, our resolution method

needs to be of “order zero”. These methods corre-

spond to gradient-free optimization methods (such as

EDA optimization, simulated annealing or genetic al-

gorithms). However, such methods require numerous

computations of M(·), each of them being costly in

terms of calculation resources because each implies

performing all the steps of the RL algorithm for which

the problem is deﬁned. While the reduced number of

variables in θ helps leveraging this computational bur-

den, experience dictates it cannot make it negligible.

So this second constraint of M’s evaluation cost must

be carefully taken into account when choosing the op-

timization method.

4 OSS(N), TREE-BASED FQI AND

CROSS-ENTROPY SEARCH

In this section, we deﬁne an instance of OSS(N) by

using tree-based FQI as policy inference(·), Monte-

Carlo simulation as score(·), and Cross-Entropy

search as the optimization technique.

A simple and efﬁcient way of searching for a func-

tion’s maximum — when computing its gradient is

not possible — consists in transforming this deter-

ministic problem into a so-called associated stochas-

tic problem

(Kroese et al., 2006). Cross-Entropy

(CE) search (Rubinstein and Kroese, 2004) is one of

the methods that proved successful in this framework.

The key idea of CE search, applied to our RL set-

ting, is to let a distribution on (X ×U)

converge to-

wards the best sample set, with respect to M(θ). Al-

gorithm 2 presents, in a nutshell, the CE optimization-

based OSS method applied to the computation of an

optimal policy with the tree-based FQI

algorithm.

Algorithm 2: OSS(N) with FQI and CE search.

Input: policy inference(D) = tree-based FQI

FQI

, ;

score(µ) = Monte-Carlo evaluation of µ on a ;

set of representative initial states,;

sample(θ) = the generative model.;

CE param.: initial distrib. d on (X ×U)

, N

T S

, ρ

. ;

repeat

T =

0 ;

for i = 1 to N

T S

= draw a sampling scheme according to d ;

T ← T ∪

{

}

;

foreach sampling scheme θ

∈ T do

D = sample(θ

) ;

∗

= policy inference(D) ;

M(θ

) = score(µ

∗

);

S = sort

{

(θ,M(θ))

}

according to M(θ). ;

= (1 −ρ

)-quantile of S. ;

= elements of T having scores above M

. ;

d ← maximum likelihood distribution over S

until no more improvement in M

;

∗

= draw a sampling scheme according to d ;

return policy inference(sample(θ

∗

))

The deterministic optimization problem is transformed

into a rare event estimation problem, which is then tackled

using an adaptive density estimation algorithm.

For the sake of simplicity, we do not recall the details

on the tree-based FQI method and refer the interested reader

to (Ernst et al., 2005) for that purpose. The few parame-

ters this algorithm requires (number of iterations and tree-

related parameters) are generically denoted p

FQI

hereafter.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

The algorithm starts with an initial distribution d

over the (X ×U)

search space. A family T of N

T S

small sample sets is drawn from d, and for each sam-

ple set, the optimal policy is computed and evaluated.

This provides a set S of (θ, M(θ)) pairs, ordered by in-

creasing value of M(θ). Then, according to the impor-

tance sampling method of CE-optimization, the ρ

best θ values are selected out of the initial S set; this

provides the S

set and d is updated to ﬁt the distribu-

tion of the sample vectors in S

In the particular case of continuous states and dis-

crete actions, we chose to represent d as a product

of Gaussian densities on the continuous X space (of

dimension d

), and Bernoulli distributions on the dis-

crete U space (of size d

). More speciﬁcally, d uses a

Gaussian model for each of the Nd

continuous vari-

ables of θ and a categorical distribution for each of the

actions (which boils down to a Bernoulli distri-

bution when there are only two actions). We made the

hypothesis that all continuous variables in θ were in-

dependent, hence the covariance matrix of the global

Gaussian distribution on X

is diagonal. Although

this hypothesis can seem too naive, it still provided

good results as Section 5 will illustrate.

The main advantage of such a simple distribu-

tion model over (X ×U)

is the simplicity of its up-

date phase. According to the importance sampling

foundations of CE optimization, each Gaussian and

Bernoulli model in d is updated to ﬁt the maximum

likelihood distribution of its corresponding variable in

. Updating the Gaussian distributions on the contin-

uous variables of θ corresponds to ﬁnding the average

and the standard deviation for the associated variable

in S

. Similarly, updating the distributions over the

discrete variables (the actions) corresponds to com-

puting the new thresholds of the Bernoulli distribu-

tions, by counting the occurrences of each action in

Similarly, N

T S

(and ρ

) should be chosen by

keeping in mind that ρ

·N

T S

elements of S will be

kept in order to update the distribution d. Hence, these

·N

T S

should be informative enough to approxi-

mate a sufﬁcient statistics for the new value of d.

For domains where some previous information

(about reachability for instance) is available, the ini-

tial value of d can be designed to incorporate such

domain-speciﬁc, prior knowledge. Namely, in large

domains, random or ε-greedy initial walks can help

initialize d to non-zero values only in reachable re-

gions of the X ×U space.

The complexity of an iteration of the above

OSS(N) instance can be analyzed as follows. The

sampling phase is O(NN

T S

) and, since we train N

T S

−0.2

0.2

0.4

−1. −.5 0.0 0.5 1.

Resistance

Hill(p)

Figure 3: Car on the hill.

policies on sets of N samples with tree-based FQI

the policy training part is O(N

T S

N log(N)). Finally,

the density update phase is O(N

T S

N). So the over-

all time complexity of this OSS(N) algorithm is

O(N

T S

N log(N)).

5 EXPERIMENTS

5.1 Experimental Protocol

The “Car on the Hill” Domain. In order to il-

lustrate how the previous section’s OSS(N) method

performs in practice, and to visualize graphically

the sample set’s evolution in a two-dimensional state

space, we report optimization results on the “car on

the hill” domain. In this domain, an under-powered

car tries to reach the top of a hill, in order to escape

from a valley as illustrated on Figure 3. A positive re-

ward is gained when the car exits from the right hand

side of the domain. If the car goes too fast or exits

from the left-hand side, it receives a negative feed-

back. Otherwise, zero rewards are obtained.

The action space is composed of the two “±4N”

forces: U = {−4, 4}. The discrete-time dynamics are

obtained from the integration of the car’s law of mo-

tion, over time intervals of 0.1s. We chose to use a

γ factor of 0.95 as in (Ernst et al., 2005). With p the

horizontal position of the car, H(p) the hill’s equa-

tion, and g the gravitational constant, the continuous

time dynamics of the system are:

H(p) =

(

+ p if p < 0

√

1+5p

if p ≥ 0

¨p =

u −gH

(p) − ˙p

(p)H

(p)

1 + H

(p)

The state space of the system is spanned by the

two variables (p, ˙p) and is bounded: X = [−1; 1] ×

[−3;3] ∪

{

∞

}

. The additional state x

∞

is an abstract

Which has time complexity of O(N log(N)).

OPTIMAL SAMPLE SELECTION FOR BATCH-MODE REINFORCEMENT LEARNING

absorbing state, entered only when the car’s dynamics

let it escape the domain’s bounds (either in speed or

position). The only non-zero rewards received in this

domain are for the transition to x

∞

r(x

) =







1 if p

t+1

> 1 and | ˙p

t+1

| ≤ 3

−1 if p

t+1

< −1 or | ˙p

t+1

| > 3

0 otherwise

Initializing d. We initialized the distribution d by

using a regular paving with N Gaussian elements in

the state space and by drawing all actions at random

(Bernoulli distribution with a 0.5 threshold), as illus-

trated in Figure 5(a), in order to promote sample di-

versity. Note however that many other choices for the

initial d were possible, even the blind initialization of

all Gaussian distributions to the same value.

Choosing N, N

T S

and ρ

. Recall that the ﬁrst pur-

pose of OSS is to use batch-mode RL algorithms in

order to tackle large state-action spaces. We illustrate

its properties on small domains, in order to show one

can obtain optimal policies with small sample sets,

but the real use of OSS(N) for RL practitioners lies

in the case where the state-action space is too large to

be uniformly partitioned and where N is strongly con-

strained by the available computational resources. In

order to illustrate the ability of OSS to ﬁnd efﬁcient

policies with few samples, we report experimental re-

sults with N = 20. Note that similar results were ob-

tained with even lower values of N. We chose a value

of 500 for N

T S

with a ρ

of 0.1.

Parameters of Tree-based FQI. Tree-based FQI

presents the advantage of requiring only few param-

eters to tune. In our case, each Q-function is rep-

resented with a mixture of 200 fully-developed ex-

tremely randomized trees and 30 iterations of FQI are

performed to obtain an estimate of the Q

∗

function.

Scoring Function. We chose to evaluate a policy’s

quality by using a set of initial states corresponding

to different initial values of p and to a null initial ve-

locity. The policy’s score is the average of the ini-

tial states’ values, estimated by performing rollouts.

These initial states are seven regularly dispatched po-

sitions on the hill, with zero velocity (the small bullets

on the horizontal axis of Figures 5(a) to 5(i)).

5.2 Results

Figure 4 reports the evolution of the policy scores

throughout the algorithm’s iterations. The lowest

curve represents the evolution of the worse sample

-0.8

-0.6

-0.4

-0.2

0.2

0.4

0.6

0 5 10 15 20 25 30 35 40

score

iteration

(a) M

min

, M

and M

max

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0 5 10 15 20 25 30 35 40

score

iteration

(b) M

Figure 4: Evolution of the scores throughout the iterations.

set’s (among the set T ) value M

min

. The middle one is

the evolution of M

and the top one corresponds to

the value M

max

of the best sample set of T . The most

signiﬁcant result of this ﬁgure is the steady evolution

of the (1 −ρ

)-quantile M

since both M

min

and

max

can be due to lucky outliers. As expected, all

three scores increase with the number of iterations,

with a larger variance for M

max

and M

min

. One can

note the steady increase of M

towards the optimal

value for this domain (0.49).

An interesting property can be noted if one allows

for a slight modiﬁcation of Algorithm 2. If, instead

of returning policy inference(sample(θ)) in the end,

one stores ofﬂine the best policy obtained at each it-

eration, then, because M

max

’s high variance allows it

to reach some optimal values very early in the iter-

ations, a close-to-optimal policy can be found much

before M

converges to the optimal score. This adds

very little overhead to the algorithm since it only re-

quires one disk writing operation per iteration and can

be beneﬁcial in an anytime setting: the best policy

is stored on disk and always available for retrieval

if needed, and the probability of ﬁnding even better

policies increases with the iterations (until asymptotic

convergence of M

Figure 5 reports the graphical evolution of the

Gaussian densities of d, describing where the crucial

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

samples concentrate in the state space. The triangles

in these ﬁgures represent the samples the distributions

are computed from. Hence, in a single ﬁgure, there

are ρ

·N

T S

·N = 0.1 ·500 ·20 = 1000 samples. A

triangle oriented to the left (resp. right) stands for

a −4 (resp. +4) action. Since we chose the naive

model of uncorrelated variables, all the ellipses repre-

sented have their principal directions along the state

space’s axes. A richer covariance model might allow

for a better sample set description at the cost of a more

complex distribution parameter update phase.

The main conclusion one can draw from these re-

sults is that, by comparing the inﬂuence of different

sample sets on the optimal policy computed by FQI,

and by using a probability density-based optimiza-

tion method, we were able to identify a distribution

on the sampling scheme (Figure 5(i)) which induces

very good policies with as little as 20 samples. In

contrast, the original paper on tree-based FQI (Ernst

et al., 2005) suggests that, in average, it is necessary

to collect tens of thousands of samples via random

walk in the state space, before an optimal policy can

be found. The generalization of this experimental re-

sult indicates that instead of an ever-reﬁning process

for the sample set, batch-mode RL algorithms can

take advantage of sample set optimization, through

OSS(N) algorithms, in order to reach optimal policies

with a low number of samples.

6 DISCUSSION

6.1 Time and Space Efﬁciency

When the state-action space’s dimension becomes

large, processing times for batch-mode RL algorithms

increase dramatically, since the sample complexity

of these algorithms is often worse than linear (e.g.,

O(Nlog(N)) for tree-based FQI). At a certain point,

it might become preferable to run N

T S

sample col-

lections and policy optimizations for small policies

based on sample sets of size N, than one large compu-

tation on the very large equivalent sample set of size

T S

·N (if this computation is at all possible). More

formally, this is supported by the complexity estimate

of Section 4, which illustrates an O(N

T S

N log(N))

time per OSS iteration which can be advantageously

compared to the O(N

T S

N log(N

T S

N)) time complex-

ity of applying tree-based FQI to the huge set of N

T S

samples (recall N

T S

is the large value here, N being

ﬁxed to a small value by the user).

On the space complexity side, both approaches re-

quire O(N

T S

N) space to store the trees and the sample

sets. However, OSS can beneﬁt easily from possible

disk storage since all the sample sets are used inde-

pendently and at different times. If one allows disk

storage, then the space complexity of OSS boils down

to O(N) since an iteration of OSS(N) only requires

keeping and processing one set of size N at once.

Furthermore, it is interesting to point out that com-

puting the score of a given θ is fully independent of

any other score computation. Hence OSS methods

can be easily adapted to a setting of distributed com-

putation on several small computers and can thus take

advantage of parallel architectures, distributing the

computational burden into small light-weight tasks.

6.2 Stochastic RL Algorithms

One of the possible caveat of using a forest of ex-

tremely randomized trees for the regressor in FQI is

related to the possible variance in the results and the

associated variance in policy quality. So far, all RL al-

gorithms are implicitly supposed to be deterministic,

ie. given a ﬁxed sample set as input, they always out-

put the same result. This is not true for extremely ran-

domized trees. Their use in the general case of FQI is

still relevant because the variance in the results tends

to zero when the number of samples grows. But in

our case, since we voluntarily kept the samples num-

ber very low, we witnessed a very large variance in the

policies generated from a given set of 20 samples. To

avoid such a variance, a simple option is to increase

the number of trees in the forest, since the variance

also tends to zero with a large number of trees. Al-

though the 200 trees used per Q-function in the previ-

ous experiment were already a large forest compared

to the one reported in (Ernst et al., 2005) (which only

had 50 trees), we tried to run the OSS meta-algorithm

on FQI with even larger numbers of trees (up to 1000)

and observed the same behaviour as reported in Sec-

tion 5.2. Obviously, when using a non-deterministic

algorithm such as tree-based FQI, one cannot guar-

antee anymore that OSS will converge to a sample set

providing the optimal policy every time, but instead, it

will lead to a training set θ

∗

that provides the optimal

policy with high probability. For the case where the

variance in the results tends to zero (with a very large

number of trees or with a deterministic algorithm such

as LSPI), then this probability should tend to one.

It is also interesting to note that variance in the al-

gorithm’s output policies might actually be desirable,

since it extends the set of policies which are “reach-

able” from an N-sized sample set. Then, by allowing

the storage of the best found policies along the way,

good policies can be found early in the search process

(as Figure 4 illustrates).

These experiments highlighted an interesting (un-

OPTIMAL SAMPLE SELECTION FOR BATCH-MODE REINFORCEMENT LEARNING

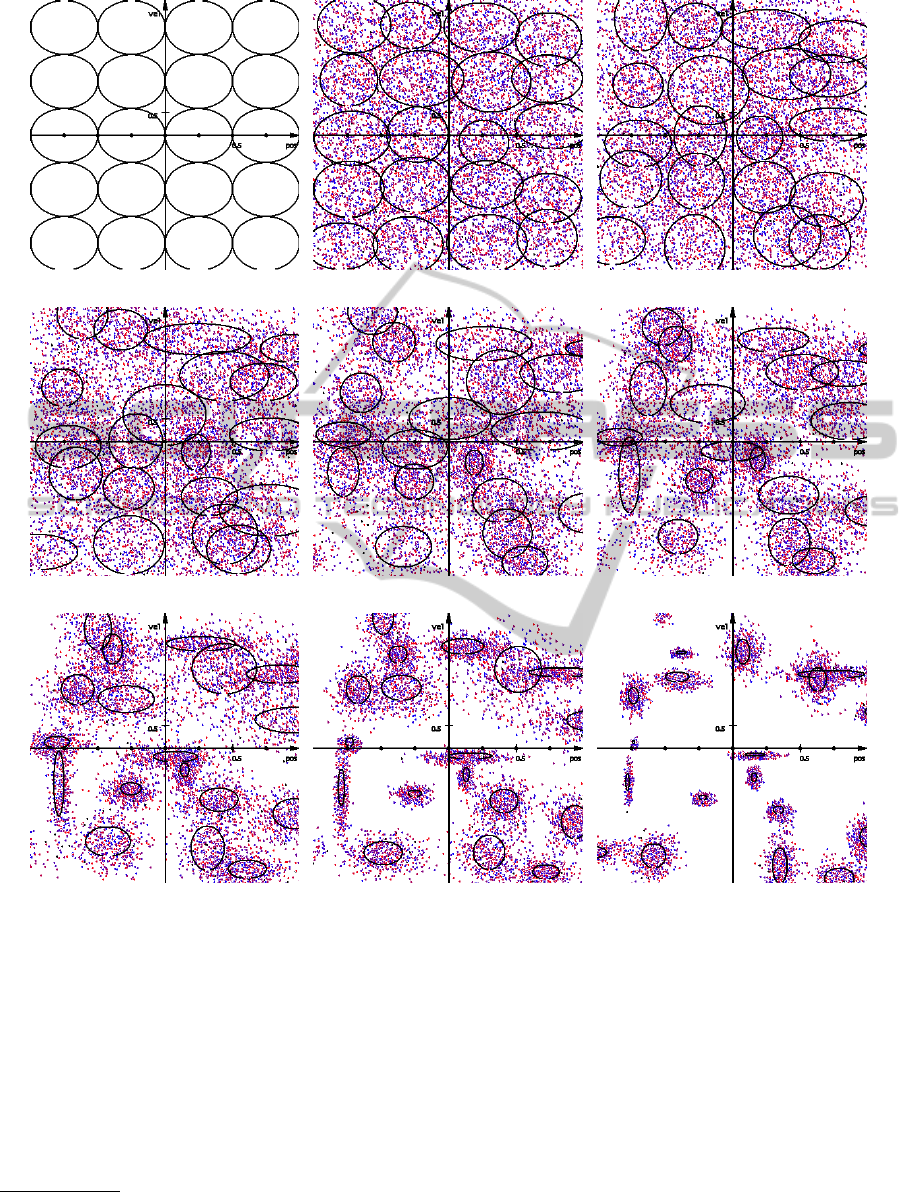
(a) Initial distribution. (b) Iteration 1. (c) Iteration 3.

(d) Iteration 5. (e) Iteration 11. (f) Iteration 16.

(g) Iteration 21. (h) Iteration 26. (i) Iteration 40.

Figure 5: Evolution of the distribution density with the iterations.

expected) property of variance reduction for OSS(20).

During the ﬁrst iterations, if several policies are

trained from a given sample set, we observe a large

variance in the output

. However, as the iteration

number grows and the distribution d concentrates on

crucial samples, we observe both an increase in the

expected value of M(θ) and a strong reduction in the

output policy’s variance: at iteration 40, when one

trains several policies using a single sample set drawn

The statistical relevance of the S

set is still insured be-

cause the large number N

T S

of sample sets averages out this

variance for the update of d.

from d, those policies both perform much better and

are much closer to each other than the ones of itera-

tion 1 were.

6.3 Dealing with Stochastic Problems

Algorithm 2 can be applied to stochastic problems

without any change. However, the results need to be

interpreted slightly differently. In stochastic domains,

the equivalence between (x,u) and (x, u,r, x

) does not

hold anymore and, thus, one needs to emphasize the

difference between the sets θ and D. As stated in Sec-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

tion 3, θ deﬁnes a sample collection scheme. Then,

ﬁnding the optimal θ consists in ﬁnding the sample

collection scheme that will lead to the best expected

policy, with respect to the transition model’s distribu-

tions.

Indeed, in Section 3, we did not focus explicitly

on the sample collection phase since a single θ al-

ways induced the same D set in the deterministic set-

ting. But, in the stochastic case, one cannot make use

of such a shortcut and one should note that we do not

compute µ

∗

anymore, but an optimal policy ˆµ

∗

for one

possible training set D, drawn according to θ, among

many others. This clariﬁcation raises the question of

sampling several D from θ to assess the true value of

M(θ). But, as for the variance reduction property of

the previous section, we argue one does not need to do

so and, instead, can rely on the large number of θ val-

ues drawn from d to average out the different possible

D sets. This question remains open nevertheless and

should be addressed in more detail in future research.

6.4 Related Work

In order to collect relevant sample sets for batch-mode

RL algorithms, the naive approach of uniform grid

sampling across the state-action space does not scale

to high-dimensional domains since the RL algorithms

become very slow (if able at all) at processing this ex-

ponentially increasing amount of data. We mentioned

earlier the domain-speciﬁc approaches of (Neumann

and Peters, 2009; Riedmiller, 2005; Ernst et al., 2006;

Kalyanakrishnan and Stone, 2007). In the latter, the

authors alternate a policy computation and a sample

gathering phase, where the sample gathering is a care-

fully tuned ε-greedy exploration, with respect to the

last computed policy, regularly reset to the start state.

All the discovered samples are then added to the sam-

ple set and the optimal policy is recomputed. Such

data collection schemes rely on Monte-Carlo explo-

ration methods and present similarities with online-

RL approaches, which provide reachability guaran-

tees while incrementally extending the sample set.

In general, these methods suffer from two defaults,

which come in contrast with the OSS approach:

• They often require a lot of domain speciﬁc hand-

tuning to be efﬁcient.

• They keep on enriching the sample set, letting it

grow up to a point where its size becomes again

problematic for the batch-mode RL method.

The work of (Ernst, 2005) presents a method to select

concise sets of samples for the same tree-based FQI

algorithm than the present work. But their goal and

approach was very different: instead of searching for

the best possible ﬁxed-size set of samples, they started

with a very large constrained sample set and tried to

extract a subset that would still provide policies with

good performances, without requiring any extra sam-

pling from a generative model. They based their ap-

proach on a Bellman error criterion and illustrated a

pathological case where the subset found critically

concentrates samples around Q-function discontinu-

ities. It is also interesting to note that the reported

original motivation of their paper conﬁrms ours: their

goal being to “lighten the computational burden of

running the ﬁtted Q-iteration algorithm on the whole

set of four-tuples”.

Finally, Cross Entropy methods, such as the one

used in our experiment, have been quite widely used

in recent years in the RL literature, for instance for

the task of reﬁning policies for Tetris (Szita and

orincz, 2006), or for adapting feature functions for

linear architectures (Menache et al., 2005), or to opti-

mize fuzzy state space partitions for fuzzy Q-iteration

(Bus¸oniu et al., 2008). An interesting parallel can be

made between the latter approach and the present one:

they deﬁne fuzzy partitions for the value function, im-

plicitly identifying speciﬁc areas in the X ×U space,

similar to the areas of interest deﬁned for samples by

our density-based optimization method. Although CE

search is not an imperative choice for OSS (other op-

timization methods are available), it seems to be well

suited to handle the large dimensional, gradient-less

optimization problems that arise in RL.

7 CONCLUSIONS

We introduced the Optimal Sample Selection meta-

algorithm, in order to generate optimal policies for

large sequential control problems. This approach con-

sists in looking directly for a set of training exam-

ples that — given a batch-mode RL algorithm —

will induce an optimal policy for the domain at hand.

More speciﬁcally, an OSS(N) algorithm takes as in-

put a generative model, a batch-mode RL algorithm,

an evaluation procedure, then deﬁnes the search for

an optimal set of N training examples as an optimiza-

tion problem, and ﬁnally solves it using a stochastic

optimization method. The instance of OSS we tested

uses tree-based ﬁtted Q-iteration as the batch-mode

RL algorithm, evaluates a policy by generating trajec-

tories to compute its average return over a set of ini-

tial states and optimizes the sample set by using Cross

Entropy search. We studied this instance’s properties

under various simulation conditions. One remarkable

property of OSS(N) is that a very small set of 20 care-

fully chosen samples was sufﬁcient to generate a near-

OPTIMAL SAMPLE SELECTION FOR BATCH-MODE REINFORCEMENT LEARNING

optimal policy.

Based on these results and on other experiments

not reported in this paper, we conjecture that for

many Optimal Control problems, there exist sam-

ple sets of “acceptable size” which can lead to near-

optimal policies when used as input of batch-mode

RL algorithms and that ﬁnding these sets is compu-

tationally feasible. This leads us to believe that this

OSS meta-algorithm may perform well, where other

sampling/discretization-based resolution schemes in

Optimal Control fail, due to limitations in the size of

the sample sets that can be manipulated in a reason-

able time by a computer.

ACKNOWLEDGEMENTS

Emmanuel Rachelson acknowledges the support of

the Belgian Network DYSCO, IAP Programme.

Franc¸ois Schnitzler is supported by FRIA. Damien

Ernst is a research associate of the FRS-FNRS. The

scientiﬁc responsibility rests with the authors.

REFERENCES

Bertsekas, D. P. and Shreve, S. E. (1996). Stochastic Opti-

mal Control: The Discrete-Time Case. Athena Scien-

tiﬁc.

Boyan, J. (1999). Least-squares temporal difference learn-

ing. In Int. Conf. Machine Learning, pages 49–56.

Bus¸oniu, L., Babu

ska, R., Schutter, B. D., and Ernst, D.

(2010). Reinforcement Learning and Dynamic Pro-

gramming using Function Approximators. Taylor &

Francis.

Bus¸oniu, L., Ernst, D., Schutter, B. D., and Babu

ska, R.

(2008). Fuzzy partition optimization for approximate

fuzzy Q-iteration. In IFAC World Congress.

Ernst, D. (2005). Selecting concise sets of samples for a re-

inforcement learning agent. In Int. Conf. on Compu-

tational Intelligence, Robotics and Autonomous Sys-

tems.

Ernst, D., Geurts, P., and Wehenkel, L. (2005). Tree-based

batch mode reinforcement learning. Journal of Ma-

chine Learning Research, 6:503–556.

Ernst, D., Stan, G. B., Goncalves, J., and Wehenkel, L.

(2006). Clinical data based optimal STI strategies

for HIV: a reinforcement learning approach. In IEEE

Conference on Decision and Control.

Kalyanakrishnan, S. and Stone, P. (2007). Batch reinforce-

ment learning in a complex domain. In AAMAS, pages

650–657.

Kroese, D. P., Rubinstein, R. Y., and Porotsky, S. (2006).

The cross-entropy method for continuous multiex-

tremal optimization. Meth. and Comp. in App. Prob.,

8:383–407.

Lagoudakis, M. and Parr, R. (2003a). Least-squares pol-

icy iteration. Journal of Machine Learning Research,

4:1107–1149.

Lagoudakis, M. G. and Parr, R. (2003b). Reinforcement

learning as classiﬁcation: Leveraging modern classi-

ﬁers. In 20th Int. Conf. on Machine Learning, pages

424–431.

Menache, A., Mannor, S., and Shimkin, N. (2005). Ba-

sis function adaptation in temporal difference rein-

forcement learning. Annals of Operations Research,

134(1):215–238.

Neumann, G. and Peters, J. (2009). Fitted Q-iteration by

advantage weighted regression. In Neural Information

Processing Systems.

Ormoneit, D. and Sen, S. (2002). Kernel-based reinforce-

ment learning. Machine Learning Journal, 49:161–

178.

Riedmiller, M. (2005). Neural ﬁtted Q-iteration - ﬁrst ex-

periences with a data efﬁcient neural reinforcement

learning method. In 16th European Conference on

Machine Learning, pages 317–328.

Rubinstein, R. Y. and Kroese, D. P. (2004). The Cross-

Entropy Method: a Uniﬁed Approach to Monte Carlo

Simulation, Randomized Optimization and Machine

Learning. Springer Verlag.

Sutton, R. S. and Barto, A. G. (1998). Reinforcement Learn-

ing: An Introduction. The MIT Press, Cambridge.

Szita, I. and L

orincz, A. (2006). Learning tetris using the

noisy cross-entropy method. Neural Computation,

18(12):2936–2941.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence