AN ADAPTIVE SINGLE FREQUENCY PHASE VOCODER FOR

LOW-POWER HEART RATE DETECTION

Development of a Fast and Low-power Heart Rate Estimation Algorithm for Mobile

Phone Applications

Walter Karlen, Guy Dumont

Electrical and Computer Engineering in Medicine (ECEM), The University of British Columbia, Vancouver, Canada

Chris Petersen, Jennifer Gow, J. Mark Ansermino

Pediatric Anesthesia Research Team (PART), BC Children’s Hospital, Vancouver, Canada

Keywords:

Pulse detection, Heart rate estimation, Mobile phones, Embedded systems, Photoplethysmography, Vocoder.

Abstract:

Mobile phones can be used as a platform for clinical decision making in resource-poor and remote areas. Their

limited battery and computational resources, however, demand efﬁcient and low-power algorithms. We present

a new algorithm for the fast and economical estimation of heart rate (HR) from the photoplethysmogram (PPG)

recorded with a pulse oximeter connected to a mobile phone. The new method estimates the HR frequency by

adaptively modeling the PPG wave with a sine function using a modiﬁed phase vocoder. The obtained wave is

also used as an envelope for the detection of peaks in the PPG signal. HR is either computed using the vocoder

center frequency or the peak intervals in a histogram. Experiments on a mobile device show comparable

speed performance with other time domain algorithms. Preliminary tests show that the HR computed from

the vocoder center frequency is robust to Noise in the PPG. The instantaneous HR calculated with the vocoder

peak detection method was more sensitive to short-term HR variations than the vocoder center frequency

method. These results point to further developments using a combination of both HR estimation methods that

will enable the robust implementation of adaptive phase vocoders into mobile phone applications.

1 INTRODUCTION

Mobile health technology is a rapidly advancing ﬁeld

that holds great promise for improving medical ser-

vices and changing the way that health care is de-

livered. A common theme in this area is the use of

general purpose consumer devices, in particular smart

phones. An increasing number of health care applica-

tions use these mobile platforms to interface directly

to physiological sensors, such as heart rate (HR) de-

tectors. While this reduces or eliminates the cost of

custom embedded hardware, features such as an in-

creased noise level, limited battery and computational

resources, and the requirement for on-line processing

challenge the accurate, real-time detection of physio-

logical parameters, such as HR peaks.

In this paper, we consider the extraction of heart

rate (HR) from a photoplethysmography (PPG) signal

that originates from an oximeter sensor interfaced to

a smart phone. We propose a novel approach to com-

pute HR from the PPG signal based on a dynamically

adapted, single frequency phase vocoder algorithm.

This algorithm is intended to form a core engine for

more complex mobile signal analyzers within a fully

functional low-cost, smart phone-based pulse oxime-

ter.

1.1 Related Work

The traditional methods used for peak detection in the

ECG signal for HR estimation, which have a long his-

tory in biomedical signal processing, can be applied

to PPG signals. HR estimation algorithms operate ei-

ther in the time or the frequency domain. Common

time domain algorithms include linear and non-linear

ﬁlters, artiﬁcial neural networks, genetic algorithms,

ﬁlter banks, and heuristic methods based on nonlin-

ear transforms. Frequency domain algorithms include

various wavelet and Fourier transforms. However, not

all of these methods are suitable for on-line computa-

Karlen W., Dumont G., Petersen C., Gow J. and Mark Ansermino J..

AN ADAPTIVE SINGLE FREQUENCY PHASE VOCODER FOR LOW-POWER HEART RATE DETECTION - Development of a Fast and Low-power

Heart Rate Estimation Algorithm for Mobile Phone Applications.

DOI: 10.5220/0003134200300035

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 30-35

ISBN: 978-989-8425-37-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

tion (Kohler et al., 2002). In particular, algorithms

must be computationally efﬁcient for mobile applica-

tions, where power and computational resources are

limited. Algorithms are commonly trimmed in or-

der to achieve computational efﬁciency (Kohler et al.,

2002). However, this comes at the expense of accu-

racy and performance. Our aim was to design an ac-

curate HR estimation algorithm for PPG that requires

low processing power so as to be suitable for battery-

powered mobile applications.

2 ALGORITHM DEVELOPMENT

Since cardiac signals are quasi periodic, a time-

frequency transformation algorithm could be appro-

priate to extract HR. However, Fourier or wavelet

based transformations on time series require segmen-

tation of the signal, which is not always practical in an

on-line, low-cost system. Their relatively high pro-

cessing power and memory usage requirements add

to this unsuitability. Instead, we propose to operate in

the time domain, using a methodology inspired by the

phase vocoder originally developed for the compres-

sion of voice signals in telecommunications (Flana-

gan et al., 1965). In this method, a vocoder models

the input signal with one or multiple sinusoidal waves

that vary in time. The parameters that have to be es-

timated are the time varying amplitude and frequency

of each sine wave that comprises the original signal.

The phase vocoder can be seen as a ﬁlter bank con-

sisting of a series of band-pass ﬁlters with successive

center frequencies (Dolson, 1986).

In our case, we are solely interested in the dom-

inant frequency in the signal (the heart beat). It is,

therefore, sufﬁcient to represent the input signal by

only one sinusoidal wave that varies over time. The

ﬁlter-bank with a distinguished set of frequencies is

replaced with a single band-pass ﬁlter whose center

frequency is adapted over time. This can be achieved

by scanning the incoming signal and computing the

difference in phase. The obtained frequency parame-

ter, where the system eventually locks-in, can be seen

as a ﬁltered frequency of the incoming signal that

would correspond to an averaged HR. The method

can also ﬁnd the location in time of each heart beat

by using the output sine wave as an envelope to locate

maximal peaks in the input waveform.

2.1 Algorithm Description

The raw PPG signal is high-pass ﬁltered to remove

the baseline using a second-order Butterworth ﬁlter

with a cut-off frequency at 0.5 Hz (Figure 1-1). The

ﬁltered signal is then routed into two parallel streams.

The signal is multiplied by a sine wave in one stream

and by a cosine wave in the other (Figure 1-2). Co-

sine and sine waves have the same unitary amplitude

and frequency w

. The frequency w

is set to the es-

timated vocoder frequency of the previous iteration

(Figure 1-8). The two parallel streams are, therefore,

identical with the exception of the π/2 shifted phase

of the multiplying waveform. This step creates a new

signal that is composed of two periodic signals with

shifted frequencies of ±w

as follows:

cos(w

∗t) ∗cos(w

∗t) =

cos((w

−w

) ∗t) + cos((w

+ w

) ∗t),

(1)

where w

is the frequency of the incoming wave at

timestep t. Next, each of the two streams is fed to

a moving average low-pass ﬁlter (Figure 1-3). The

application of this heterodyning step has two effects.

First, input frequencies in proximity of the vocoder

frequency w

are shifted down close to DC and are

allowed to pass the ﬁlter. All other frequency compo-

nents will also be shifted but they will not go through

the low-pass ﬁlter. Secondly, the heterodyning pro-

vides a way to compute the time-varying amplitude

and frequency of the resulting signal in the next step.

The two ﬁltered waveforms are subsequently trans-

formed from Cartesian to Polar coordinates to obtain

a single amplitude r

and phase θ

(Figure 1-4). The

amplitude is calculated as the square root of the sum

of the squares of the two heterodyned signals as fol-

lows:

= 4 ∗

sin

∗y

cos

, (2)

where y

sin

and y

cos

are the heterodyned signals for the

sine and the cosine streams, respectively. Similarly,

at each point in time t is the angle whose tangent

is the ratio of the vertical to the horizontal position as

follows:

= arctan(

sin

cos

). (3)

The phase is subsequently unwrapped. The real time-

varying frequency of the original wave is then esti-

mated by computing the difference between the ac-

tual and previous phase (Figure 1-5), and subtracting

it from the current center frequency (Figure 1-6) as

follows:

ˆw

= w

−1

)

−∆θ, (4)

where ∆θ = θ

−1

)

−θ

. The amplitude and the newly

computed center frequency are used to compute the

vocoder output y

out

(Figure 1-7) as follows:

out

= r

∗sin(2 ∗π ∗w

∗t). (5)

The output signal frequency w

is also used to esti-

mate the instantaneous HR. Algorithm 1 shows a pos-

sible implementation of the adaptive single-frequency

phase vocoder in pseudo C code.

AN ADAPTIVE SINGLE FREQUENCY PHASE VOCODER FOR LOW-POWER HEART RATE DETECTION -

Development of a Fast and Low-power Heart Rate Estimation Algorithm for Mobile Phone Applications

8 6

z

∆θ

z

Figure 1: Operation of the adaptive single-frequency phase

vocoder: (1) high-pass ﬁlter to remove DC value, (2) het-

erodyning the input with both a sine and a cosine wave in

parallel, and a (3) low-pass ﬁlter, (4) converting the two sig-

nals from rectangular to polar coordinates and unwrapping

the angular-position values, (5) subtracting successive un-

wrapped angular-position values, (6) subtracting the phase-

difference from the previous center frequency to obtain the

new center frequency, (7) generating the vocoder output

wave for peak detection, and (8) feeding the center fre-

quency back into the heterodyne function.

Algorithm 1: Adaptive Phase Vocoder.

1: initialization

2: while TRUE do

3: val = input

4: val ← highpass(val)

5: y

sin

← lowpass(val ∗sin( f req

−1

∗t));

6: y

cos

← lowpass(val ∗cos( f req

−1

∗t));

7: phase ← unwrap(atan2(y

sin

cos

), phase

−1

)

 unwrap the phase

8: ampl ← 4 ∗

√

sin

∗y

sin

+ y

cos

∗y

cos

9: f req ← f req

−1

−(phase

−1

−phase) adjust

frequency to lock onto the waveform

10: if f req < 0.00001 then  clamp to avoid

negative frequency values

11: f req ← 0.00001

12: end if

13: end while

To detect the location of the HR peaks, the mono-

phone sinusoidal vocoder output y

out

is used as an in-

dicator of the approximate location of the peaks in

the actual PPG waveform. The simple form of the

vocoder waveform reduces the problem of detecting

peaks in the noisy PPG signal to a straight-forward

search for the maximum amplitude within the tem-

poral interval of a positive half cycle of the vocoder

output signal. The time elapsed from the previously

detected peaks is binned into a moving histogram of

heart rate intervals. This serves to eliminate artifacts

caused by motion and other spurious effects, with the

largest histogram bin giving a direct representation of

the instantaneous HR. The sensitivity of this peak de-

tection method can be adjusted by offsetting the si-

nusoidal vocoder signal; a positive or negative offset

adjustment will result in a wider or narrower positive

half cycle interval, respectively.

2.2 Algorithm Validation

In order to test the algorithm, following institutional

review board approval, data was gathered from nine

children (1-7 years old, 14 kg ± 6.2) who underwent

general anesthesia. The recordings obtained included

ECG, capnometry, and PPG signals. All signals were

recorded with Collect S/5 software (Datex-Ohmeda,

Finland) using a sampling frequency of 300Hz. An 8-

minute segment of reliable recording of spontaneous

breathing was selected from each case. These seg-

ments are available from the on-line database Cap-

noBase.org (Karlen et al., 2010).

The ECG waveform was used as the reference

recording for computing HR. A technician indepen-

dently validated the reference measurement using the

CapnoBase Signal Evaluation Tool (Karlen et al.,

2010). The mean HR of a sliding window was calcu-

lated. The window size was set to 20 s; a size that cor-

responds to that commonly used in commercial pulse

oximeters.

The performance of the adaptive algorithm was

assessed using the normalized root mean square

(NRMS) error (%) of the calculated HR from the

vocoder output frequency. The NRMS error corre-

sponds to the square root of the sum of the squares

of the differences between the test and reference HR

measurements, divided by the sum of the reference

measurements:

NRMS error =

∑

i=1

re f

−x

alg

)

∗n

∑

i=1

re f

. (6)

A measurement error was calculated for each test

measurement by comparing it with the reference mea-

surement that was nearest to it in time. The ﬁrst 50s

were used to initialize the high-pass ﬁlters and the

vocoder sliding window, and so were not analyzed.

To evaluate the computational load of the algo-

rithm executed on a mobile device, we built a pro-

totype device consisting of a PureLight medium soft

sensor connected to an Xpod OEM module (Nonin,

Plymouth, USA) (Figure 2). The module was con-

nected to a 2

generation iPod Touch (Apple, Cuper-

tino, USA). The iPod Touch displayed the PPG wave-

form and recorded the continuous data stream. The

PPG was recorded with a 16bit resolution at a sam-

pling rate of 75 Hz. The algorithm was implemented

in C and embedded into the iOS application software,

called Phone Oximeter

, to process the raw PPG sig-

nal in real-time. The computational load was mea-

http://www.phoneoximeter.org

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

Figure 2: Phone Oximeter (Mobile phone pulse oximeter)

application. 1) Soft ﬁnger probe; 2) Nonin Xpod OEM

pulse oximeter module; 3) raw PPG waveform display on

iPod Touch; 4) SpO2 value computed by the Xpod module;

5) HR computed by the adaptive vocoder algorithm.

sured in microseconds using interrupts during pro-

gram execution.

For comparison, we implemented into the iOS ap-

plication two other HR estimation methods. The ﬁrst

used the Pan-Tompkins algorithm (Pan and Tomp-

kins, 1985). This time domain based method makes

use of a cascade of band-pass ﬁlter, integrator, squar-

ing, and differentiators. An adaptive threshold was

applied to detect the heart beat pulses. The second

method calculated the power spectral density with a

Fast Fourier Transform (FFT) algorithm from (Press

et al., 1992) that was implemented in the C library

from (Goldberger et al., 2000). A 50s window size

was selected, border effects were reduced using a

Hamming windowing function, and the maximum

power band was chosen to estimate the HR. The FFT

was recalculated every second by shifting the window

by 75 samples.

3 RESULTS

The parameters used in the adaptive vocoder algo-

rithm are shown in Table 1.

With an average NRMS error of 3.33% (Table

2), the HR calculated directly from the vocoder out-

put frequency was accurate. However, two cases ex-

hibited higher NRMS error than the others (0030l

Table 1: Algorithm conﬁguration parameters.

Parameter Value

heterodyne low-pass cut-off frequency 0.04 Hz

initial vocoder frequency w

(0)

50 Hz

initial vocoder amplitude r

(0)

number of histogram bins 32

Table 2: Normalized root mean square (NRMS) error be-

tween the reference HR obtained from ECG and the HR

estimated by the vocoder frequency or vocoder peak detec-

tion method respectively. The last column is the mean ECG

HR used for calculating the NRMS error.

Case HR NRMS error mean HR

[%] [bpm]

vocoder vocoder ECG

freq peak

0009l 3.4979 1.7496 92.5807

0015l 0.5915 0.6440 108.454

0018l 0.5170 1.2345 127.149

0023l 2.3822 1.3859 92.3054

0028l 2.4448 2.8312 66.4234

0030l 6.8719 4.3432 107.406

0032l 2.3679 2.8300 77.2644

0035l 2.9794 1.4727 102.547

0038l 8.3220 1.2452 108.462

Average 3.3305 1.9707 98.0658

and 0038l). Closer inspection of these cases illus-

trates that reduced performance of the vocoder fre-

quency HR is mainly due to its low responsiveness to

a rapidly changing HR of more than 10bpm (Figure 3

and 4).

With an average NRMS error of 1.97% (Table 2),

the HR calculated from the vocoder peak detection

using histograms was more accurate than the vocoder

frequency estimations. The disagreement between

ECG reference HR and HR obtained from vocoder

peak detection resulted from a delay in the HR estima-

tion of the latter; a 5s to 10s delay observed through-

out these cases can be attributed to the size of the his-

togram for HR calculation. Cases 0028l, 0030l, and

0032l showed greater decreases in performance than

the mean of the cases. In these cases, the poor quality

of the PPG signal prevented the vocoder peak detec-

tion algorithm from accurately estimating HR (Figure

3). The vocoder peak detection was able to track fast

variations and compensate for the low responsiveness

of the direct vocoder frequency calculation.

The adaptive vocoder algorithm including peak

detection required an average of 47.33 us to pro-

cess a new value, which was slower than the Pan-

Tompkins algorithm (Table 3). Both were signiﬁ-

cantly faster than the inter-sampling distance of 13.3

AN ADAPTIVE SINGLE FREQUENCY PHASE VOCODER FOR LOW-POWER HEART RATE DETECTION -

Development of a Fast and Low-power Heart Rate Estimation Algorithm for Mobile Phone Applications

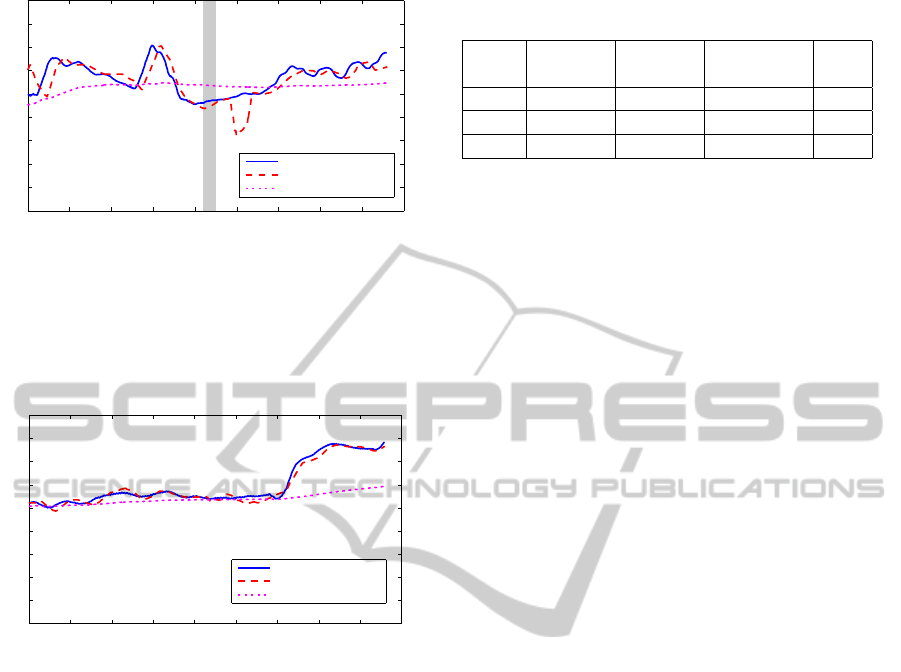
PPG Artifacts

50 100 150 200 250 300 350 400 450 500

100

110

120

130

140

150

time [s]

heart rate [bpm]

Case 0030l

HR (ECG)

HR (vocoder peak)

HR (vocoder freq)

Figure 3: HR agreement comparison for Case 0030l. The

HR calculated by the vocoder peak method is degraded af-

ter a time offset (at 300s) when the raw PPG signal was cor-

rupted with noise over a certain period of time (gray bar).

The HR estimated by the vocoder frequency is smoothed

out and does not respond quickly to large variations in HR.

50 100 150 200 250 300 350 400 450 500

100

110

120

130

140

150

time [s]

heart rate [bpm]

Case 0038l

HR (ECG)

HR (vocoder peak)

HR (vocoder freq)

Figure 4: HR agreement comparison for Case 0038l. The

HR estimated by the vocoder frequency does not respond

rapidly to a large permanent change in HR after 350s. The

HR calculated by the vocoder peak method is accurately

following the ECG HR trend.

ms. The algorithms can be computed in real-time on

the phone while sufﬁcient processing power is avail-

able for other computing tasks. The FFT HR esti-

mation method was about 40 times slower than the

vocoder algorithm (Table 3).

4 DISCUSSION

We can conclude from these preliminary tests that the

major design criteria of accuracy and on-line capabili-

ties for a mobile phone HR estimation algorithm were

met. With an average accuracy of 1.97% NRMS, the

HR prediction is acceptable for a mobile device. The

speed tests show that the proposed algorithm achieves

this within the range of traditional ﬁltering methods

and faster than frequency domain-based approaches.

The adaptive vocoder frequency output ﬁltered

short variations in HR and PPG artifacts effectively.

Table 3: Algorithm execution time per sample on the iPod

Touch calculated over 16 measurements of one minute.

Vocoder Vocoder Pan- FFT

freq peak Tompkins

[us] [us] [us] [us]

Mean 41.25 47.33 28.84 1937

SD 0.9 0.8 0.45 4.06

However, the algorithm was not able to detect large,

rapid changes in HR and lock into the new frequency

in a reasonable amount of time. The vocoder respon-

siveness could be improved by tuning the cut-off fre-

quency of the low-pass ﬁlter shown in Figure 1-3. On

the other hand, the vocoder peak detection method

was able to rapidly track changes in HR. However,

this attribute made it more vulnerable to errors when

the PPG was corrupted with noise.

It is, therefore, evident that the advantages and

drawbacks of the two approaches are complemen-

tary. A logical step would be the combined use of

these vocoder based HR extraction methods. A sys-

tem that detects short-term variations with the peak

detection and long-term trends with the vocoder fre-

quency could provide increased diagnostic informa-

tion.

A desired improvement to the vocoder peak HR

estimation algorithm is to reduce the delay that was

introduced by the histogram detection algorithm. We

also plan to increase its robustness to poor quality

PPG signals by adding a signal quality index to the al-

gorithm. Active detection of poor signal will prevent

the erroneous HR output and increase overall estima-

tion performance.

Although we compared processing speed of dif-

ferent HR estimation algorithms when embedded into

a mobile device, we did not compare the estimation

performance between these methods in this study. We

plan to proceed with a performance comparison as

soon we have implemented the suggested improve-

ments in a prototype device. This will allow us to

conduct clinical studies for validation on an increased

number of cases.

5 CONCLUSIONS

A novel approach to compute HR based on a dynam-

ically adapted, single frequency phase vocoder algo-

rithm was proposed. Initial experiments showed good

accuracy and low computational costs for the sug-

gested approach. The robustness of the algorithm to-

wards noise in the plethysmogram waveform was an-

other strength. This makes the algorithm suitable to

process on-line PPG signals that are recorded from an

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

oximeter sensor interfaced to a smart phone. We in-

tend to use the algorithm as a core engine for more

complex mobile signal analyzers (i.e. for the estima-

tion of heart rate variability or respiratory rate) within

a smart phone based pulse oximeter. The suggested

algorithm has the potential to be applied to other pe-

riodic signals whose frequency range has to be deter-

mined in real-time.

REFERENCES

Dolson, M. (1986). The Phase Vocoder: A Tutorial. Com-

puter Music Journal, 10(4):14–27.

Flanagan, J. L., Meinhart, D. I. S., Golden, R. M., and

Sondhi, M. M. (1965). Phase Vocoder. The Journal

of the Acoustical Society of America, 38(5):939–940.

Goldberger, A. L., Amaral, L. A. N., Glass, L., Hausdorff,

J. M., Ivanov, P. C., Mark, R. G., Mietus, J. E., Moody,

G. B., Peng, C.-K., and Stanley, H. E. (2000). Phys-

ioBank, PhysioToolkit, and PhysioNet: Components

of a New Research Resource for Complex Physiologic

Signals. Circulation, 101(23):e215—-e220.

Karlen, W., Turner, M., Cooke, E., Dumont, G., and Anser-

mino, J. M. (2010). CapnoBase: Signal database and

tools to collect, share and annotate respiratory signals.

In Annual Meeting of the Society for Technology in

Anesthesia (STA), page 25, West Palm Beach.

Kohler, B., Hennig, C., and Orglmeister, R. (2002). The

principles of software QRS detection. IEEE Engineer-

ing in Medicine and Biology Magazine, 21(1):42–57.

Pan, J. and Tompkins, W. J. (1985). A real-time QRS de-

tection algorithm. IEEE transactions on bio-medical

engineering, 32(3):230–6.

Press, W., Teukolsky, S., Vetterling, W., and Flannery, B.

(1992). Numerical recipes in C: the art of scientiﬁc

computing. Cambridge University Press, New York,

2nd edition.

AN ADAPTIVE SINGLE FREQUENCY PHASE VOCODER FOR LOW-POWER HEART RATE DETECTION -

Development of a Fast and Low-power Heart Rate Estimation Algorithm for Mobile Phone Applications