THE MAMDANI CONTROLLER IN PREDICTION

OF THE SURVIVAL LENGTH IN ELDERLY GASTRIC

PATIENTS

Hang Zettervall, Elisabeth Rakus-Andersson

Department of Mathematics and Science, Blekinge Institute of Technology, 371 79 Karlskrona, Sweden

Henrik Forssell

Blekinge Competence Center, 371 81 Karlskrona, Sweden

Keywords: Fuzzy control, Mamdani controller, Survival length for gastric cancer patients.

Abstract: Strict analytic formulas are the tools derived for determining the formal relationships between a sample of

independent variables and a variable which they affect. If we cannot formalize the function tying the

independent and dependent variables then we will utilize fuzzy control actions. The algorithm is particularly

adaptable to support the problem of prognosticating the survival length for gastric cancer patients. We thus

formulate the objective of the current paper as the utilization of fuzzy control action for the purpose of

making the survival prognoses.

1 INTRODUCTION

Expert-knowledge designs IF-THEN together with

assumptions of fuzzy set theory have given rise to

the creation of fuzzy control (Mamdani and Assilian,

1973; Nguyen et al., 2002; Andrei, 2005).

Typical applications of fuzzy control have

mostly concerned technical processes but, in the

current paper, we intend to prove fuzzy control to

make prognoses of the survival length in patients

with diagnosis gastric cancer.

In the first trials of survival approximation a

survival curve from censored data was introduced

(Kaplan and Meier, 1958). The model was used in

cancer patient examinations to estimate the length of

living (Newland et al., 1994). The Cox regression

(Cox, 1972) of life length prediction was developed

in such studies as logistic Cox regression (Sargent,

2001). The statistics-based models predicting the

survival were compared by Everitt and Rabe-

Hesketh (2001) who found such model

disadvantages as the lack of normal distribution or

missing values among survival times.

The development of computational intelligence

brought neural networks as a tool of approximating

the life length for cancer patients (Burke et al., 2001;

Grumett et al., 2003).

We prove the action of Mamdani controller,

which has not been adapted yet to estimation of

survival. We count on reliable results to place the

controller among other life approximation models.

2 VARIABLE FUZZIFICATION

Fuzzy control model is applied when we cannot

formalize the functional connection between

independent and dependent variables.

We expect to evaluate the survival length in

patients with diagnosis “gastric cancer”. Variable Z

= “survival length” is affected by X = “age” and Y =

“CRP-value”, selected as the most essential markers

of making the prognosis. Since the formula

(

)

yxfz ,

, x∈X, y∈Y, z∈Z, is not known then we

will test the action of fuzzy control.

All variables are divided into levels, which are

expressed by lists of terms. The terms are

represented by fuzzy sets, restricted by the

parametric s-functions lying over the variable

domains

[

]

maxmin

, xx

[

]

maxmin

, yy

and

[]

maxmin

, zz

283

Zettervall H., Rakus-Andersson E. and Forssell H..

THE MAMDANI CONTROLLER IN PREDICTION OF THE SURVIVAL LENGTH IN ELDERLY GASTRIC PATIENTS.

DOI: 10.5220/0003134402830286

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 283-286

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

We introduce five levels into

and

denoted by X

, Y

and Z

, i, j, k = 0,...,4.

A family of fuzzy set membership functions

corresponding to X

will be expressed by the

parametric

-class functions

()

split in

()

xleft

and

()

xright

(Rakus-Andersson,

2007; Rakus-Andersson et al., 2010) where

()

()()

()

⎪

⎩

⎪

⎨

⎧

⋅+≤≤⋅+−

−

⋅+−≤≤⋅+−

⋅+−

⋅+−−

if21

if2

min

minmin

min

ihxxihx

ihxxihhx

xleft

ihxx

ihhxx

(1)

and

()

()()

()

⎪

⎩

⎪

⎨

⎧

⋅++≤≤⋅++

⋅++≤≤⋅+

−

⋅++−

⋅+−

if2

if21

min

minmin

min

ihhxxihx

ihxxihx

xright

XXX

ihhxx

ihxx

(2)

Formulas (1) and (2) are affected by

min

and by

the parameter value h

, which measures the length

between the beginnings of two adjacent functions X

The h

quantity is adjusted to the number of X-

functions and to the distance between x

min

and x

max

The functions of Y

, j = 0,…,4, are constructed as

similar to (1) and (2) for the accommodated values

of parameters h

and Y

min

to the conditions of Y.

The Z

’s functions

()

, k = 0,…,4, are split

()

zleft

(

)

zmiddle

and

()

zright

()

⎪

⎩

⎪

⎨

⎧

⋅+≤≤⋅+−

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅+−≤≤⋅+−

⎟

⎠

⎞

⎜

⎝

⎛

⋅+−

⋅+−−

if21

if2

min

khzzkhz

zleft

khzz

(3)

()

if1

minmin

zzkhz

zmiddle

⋅++≤≤⋅+

(4)

and

(

)

(

)

()

⎪

⎩

⎪

⎨

⎧

⋅++≤≤⋅++

⎟

⎠

⎞

⎜

⎝

⎛

⋅++≤≤⋅++

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅++−

if2

if21

min

khhzzkhz

khzzkhz

zright

ZZZ

khhzz

khzz

(5)

The parameter h

allows designing five functions

of fuzzy sets from Z over [z

min

, z

max

Variable X will be restricted over [0, 100]. We

thus state

min

and

4,...,0=i

. For the

terms of “age” we will get by (1) and (2) the set of

membership functions sketched in Fig. 1.

20 -10 0 10 20 30 40 50 60 70 80 90 100 110 120

0.2

0.4

0.6

0.8

1.0

(

)

X ""

Figure 1: The membership functions for ”age”.

By inserting parameters of y

min

and h

in (1) and

(2), where x is replaced by y, we generate the

membership functions for “CRP-value” over [0, 50]

with

and j = 0,...,4 to plot them in Fig. 2.

-10 0 10 20 30 40 50 60 70

0.2

0.4

0.6

0.8

1.0

(

)

Y ""

Figure 2: The membership functions for ”CRP-value”.

The output variable

takes the values in [0, 5].

We determine

and set

4,...,0=k

in (3), (4)

and (5) to initialize the functions depicted in Fig. 3.

0 1 2 3 4 5

0.2

0.4

0.6

0.8

1.0

(

)

Z ""

Figure 3: The membership functions for the ”survival

length”.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

284

3 THE LOGICAL RULES

IF-THEN AND OUTPUT

DEFUZIFICATION

After the fuzzification procedure we determine rules,

which link the states of two input variables to the

state of the output variable. We design Table 1 with

entries filled with terms of “survival length”.

Table 1: Rule base of fuzzy controller estimating “survival

length”.

Some entries in the table are empty, since the

essential data was lacking for younger people.

We want to make the survival prognosis for

()

yx,

, x∈X, y∈Y. Value

can belong to more than

one fuzzy set

with different membership degrees

()

. Element

associated to x is a member of

some

with degrees

(

)

. By means of the IF-

THEN statements from Table 1 we determine the

contents of rules

Rule

()

:, lyx

and

, then

(6)

where l is the rule number.

To evaluate the influence of the input variables

on the output consequences we estimate

()

(

)()

(

)

lYlyx

::,

,min

(7)

for each

and

concerning the choice of (x,y).

Consequences of all rules R

(x, y):l

become fuzzy

sets

conseq

lyx

:),(

, which are stated in Z as

()

(

)

lZlyx

conseq

klyx

::,

,min

μαμ

(8)

We aggregate the consequence sets

conseq

lyx

:),(

one common set

),( yx

conseq

allocated in Z over a

continuous interval [z

, z

] due to

()

(

)

conseq

lyxyx :,),(

max

μμ

(9)

In order to assign a crisp value z to the selected

pair (x, y) we defuzzify the consequence fuzzy set

(9) in Z. We are furnished with the formula

()

∫

⋅

conseq

dzz

dzzz

yxfz

(10)

Example

Let

and

. Age 77 belongs to fuzzy set

= “old”. Therefore, for i = 3, h

= 0.25 and x

min

= 0 the membership degree

()

=77

9872.0

= “very old”

()

0128.077

. CRP-

value y = 16 fits for sets:

= “low” with

(

)

991.0

and

= “medium” with

()

009.016

In accordance with (6) we find the rules

()

1:16,77

IF X is X

and Y is Y

THEN Z is Z

()

2:16,77

IF X is X

and Y is Y

THEN Z is Z

()

3:16,77

IF X is X

and Y is Y

THEN Z is Z

()

4:16,77

IF X is X

and Y is Y

THEN Z is Z

For

()

() ()

(

)

,9872.016,77min

1:1:1:16,77

()

,009.0

2:16,77

()

0128.0

3:16,77

and

()

4:16,77

009.0

, due to (7), we establish consequence sets (8)

to determine the final consequence

),( yx

conseq

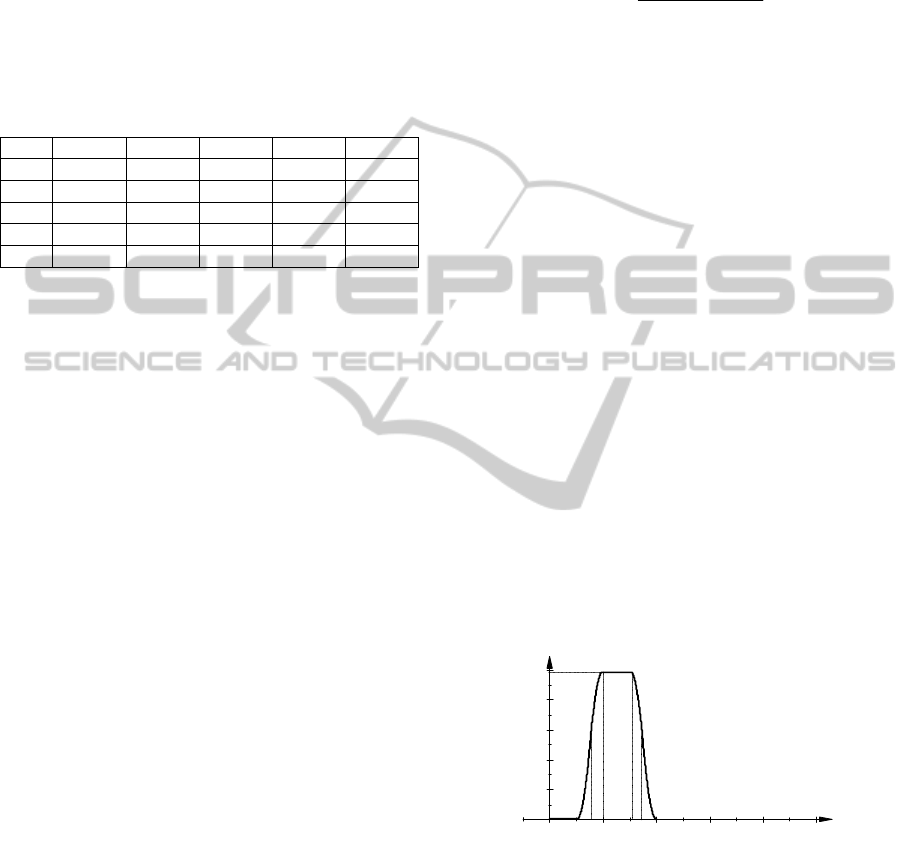
which fits for (9) and is shown in Fig. 4.

(

)

conseq

Figure 4: The consequence set conseq

(77,16)

in Z.

Formula (10) constitutes a basis of an estimation

of the survival length expected when assuming

“age” = 77 and “CRP-value” = 16. Over interval [z

] = [0, 2], which contains characteristic points z

0, z

= 0.533, z

= 0.75, z

= 0.96, z

= 1.54, z

= 1.75

and z

= 2, we compute the z-prognosis

THE MAMDANI CONTROLLER IN PREDICTION OF THE SURVIVAL LENGTH IN ELDERLY GASTRIC

PATIENTS

285

05.1)16,77(

75.1

5335.0

75.1

5335.0

5.0

2009.0

5.0

2009.0

===

∫

⎟

⎠

⎞

⎜

⎝

⎛

−

∫

⎟

⎠

⎞

⎜

⎝

⎛

−

∫

dzz

The result converges with the physician’s own

judgment. For each pair (x,y) we can arrange new

actions of the fuzzy control algorithm to estimate the

patient’s period of surviving.

4 CONCLUSIONS

Fuzzy control system is a powerful method, which

mostly is applied to technologies controlling

complex processes by means of human experience.

In this work we have proved that the expected values

of patients’ survival lengths can be estimated even if

the mathematical formalization between independent

and dependent variables is unknown. For each x and

each y belonging to continuous spaces X and Y

respectively, we can repeat the control algorithm in

order to cover the space of pairs over the Cartesian

product of X and Y with a continuous surface.

We should emphasize that the Mamdani control

system does not need any special assumptions such

as distributions of variables, regularity and others,

which are necessary to be fulfilled in statistical

survival tests (see discussion in Section 1).

The authors’ special contribution is the

mathematically formalized design of membership

functions assisting variable levels.

ACKNOWLEDGEMENTS

The authors thank Blekinge Research Board for the

grant funding the accomplishment of the current

research.

REFERENCES

Andrei, N., 2005. Modern control theory: a historical

perspective. Research Institute for Informatics, Centre

for Advanced Modelling and Optimization, Romania,

http://www.ici.ro/camo/neculai/history.pdf

Burke, H. B., Goodman, P.H., Rosen, D. B., Henson, D.

E., Weinstein, J. N., 2001. Artificial neural networks

improve the accuracy of cancer survival prediction.

Cancer, 91, 857–862.

Cox, D., 1972. Regression models and life tables. J Roy

Stat Soc B, 4, 187–220.

Everitt, B., Rabe-Hesketh, S., 2001. Analyzing Medical

Data Using S-PLUS, Springer, New York.

Grumett, S., Snow, P., Kerr, D., 2003. Neural networks in

the prediction of survival in patients with colorectal

cancer. Clin Colorect Cancer, 2, 239–244.

Kaplan, E., Meier, P., 1958. Nonparametric estimation

from incomplete observations. Journal American

Statistical Association, 53, 457–481.

Mamdani, E. H., Assilian, S., 1973. An experiment in

linguistic synthesis with a fuzzy logic controller. Int. J.

Man-Machine Studies 7, 1–13.

Newland, R. C., Dent, O. F., Lyttle, M. N., Chapuis, P. H.,

Bokey, E. L., 1994. Pathologic Determinants of

survival associated with colorectal cancer with lymph

node metastases. A multivariate analysis of 579

patients. Cancer, 73(8), 2076-2082.

Nguyen, H. T., Prasad, N. R., Walker, C. L., Walker, E.

A., 2002. A First Course in Fuzzy and Neural Control,

Chapman & Hall/CRC.

Rakus-Andersson, E., 2007. Fuzzy and Rough Techniques

in Medical Diagnosis and Medication, Springer,

Berlin Heidelberg.

Rakus-Andersson, E., Zettervall, H., Erman, M., 2010.

Prioritization of weighted strategies in the multi-player

games with fuzzy entries of the payoff matrix. Int. J.

of General Systems, Vol, 39, Issue 3, 291-304.

Sargent, D. J., 2001. Comparison of artificial networks

with other statistical approaches. Cancer, 91, 1636–

1942.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

286