EXTRACTION OF FUNCTION FEATURES

FOR AN AUTOMATIC CONFIGURATION

OF PARTICLE SWARM OPTIMIZATION

Tjorben Bogon

1,2

, Georgios Poursanidis

, Andreas D. Lattner

and Ingo J. Timm

Information Systems and Simulation, Institute of Computer Science and Mathematics

Goethe University Frankfurt, Frankfurt, Germany

Business Informatics I, University of Trier, Trier, Germany

Keywords:

Particle swarm optimization, Machine learning, Swarm intelligence, Parameter conﬁguration, Objective func-

tion feature Computation.

Abstract:

In this paper we introduce a new approach for automatic parameter conﬁguration of Particle Swarm Optimiza-

tion (PSO) by using features of objective function evaluations for classiﬁcation. This classiﬁcation utilizes a

decision tree that is trained by using 32 function features. To classify different functions we compute features

of the function from observed PSO behavior. These features are an adequate description to compare different

objective functions. This approach leads to a trained classiﬁer which gets as input a function and returns a pa-

rameter set. Using this parameter set leads to an equal or better optimization process compared to the standard

parameter settings of Particle Swarm Optimization on selected test functions.

1 INTRODUCTION

Metaheuristics in stochastic local search are used in

numerical optimization problems in high-dimensional

spaces. For varying types of mathematical functions,

different optimization techniques vary w.r.t. the op-

timization process (Wolpert and Macready, 1997). A

characteristic of these metaheuristics is the conﬁgu-

ration of the parameters (Hoos and St

utzle, 2004).

These parameters are essential for the efﬁcient opti-

mization behavior of the metaheuristic but depend on

the objective function, too. An efﬁcient set of param-

eters inﬂuences the optimization in speed and perfor-

mance. If a good parameter set is selected, an ade-

quate solution will be found faster compared to a bad

conﬁguration of the metaheuristic. The choice of the

parameters is based on the experience of the user and

his knowledge about the domain or on empirical re-

search found in literature. This parameter settings,

called standard conﬁgurations, perform a not opti-

mal but an adequate optimization behavior for most

objective functions. An example for metaheuristics

is the Particle Swarm Optimization (PSO). PSO is

introduced by (Eberhart and Kennedy, 1995) and is

a population-based optimization technique which is

used in continuous high dimensional search spaces.

PSO consists of a swarm of particles which “ﬂy”

through the search space and update their position by

taking into account their own best position and de-

pending on the topology, the best position found by

other particles. PSO is an example for the parameter

conﬁguration problem. If the parameters are well cho-

sen, the whole swarm will ﬁnd an adequate minimum

and focus on this solution. The swarm slows down

the velocity trying to get better values in the continu-

ous search space around this found solution. This ex-

ploitation can be on a local optimum especially if the

wrong parameter set is chosen and the swarm cannot

escape from this local minimum. On the other hand

the particles can never ﬁnd the global optimum if they

are too fast and never focus. This swarm behavior de-

pends mainly on the chosen parameter and leads to

solutions of different quality.

One problem in choosing the right parameters

without knowledge about the objective function is to

identify relevant characteristics of the function which

can be used for a comparison among functions. The

underlying assumption is that, e.g., a function f

= x

and a function f

= 3x

+ 2 exhibit similar optimiza-

tion behavior if the same parameter set for a Particle

Swarm Optimization is used. In order to choose a

promising parameter set, functions must be compara-

Bogon T., Poursanidis G., D. Lattner A. and J. Timm I..

EXTRACTION OF FUNCTION FEATURES FOR AN AUTOMATIC CONFIGURATION OF PARTICLE SWARM OPTIMIZATION.

DOI: 10.5220/0003134500510060

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 51-60

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ble with respect to certain objective function charac-

teristics.

We describe an approach to computing features of

the objective function by observing the swarm behav-

ior. For each function we seek for a parameter set

that performs better than the standard conﬁguration

and provide this set as output class for supervised

learning. These data allow us to train a C4.5 deci-

sion tree (Quinlan, 1993) as classiﬁer that computes

an adequate conﬁguration for the Particle Swarm Op-

timization by using function features. Experimental

trials show that our decision tree classiﬁes functions

into the correct classes in many cases. This classiﬁca-

tion can be used to select promising parameter sets for

which the Particle Swarm Optimization is expected to

perform better in comparison to the standard conﬁgu-

ration.

This work is structured as follows: In section 2 we

describe other approaches pointing out the problem

of computing good parameter sets for a metaheuristic

and explain the Particle Swarm Optimization. Section

3 describes how to compute the features of a function

and thereby make the functions comparable. After

computing the features we describe our experimental

setup and the way to build up the decision tree. Sec-

tion 4 contains our experimental results for building

the parameter classes to select promising parameter

sets in PSO. The last section discusses our results and

describes issues for future work.

2 PARAMETER SETTINGS

IN METAHEURISTICS

The main difference between solving a problem with

exact methods or with metaheuristics is the quality

of the solution. Metaheuristics – for example, na-

ture inspired metaheuristics (Bonabeau et al., 1999)

– have no guarantee of ﬁnding the global optimum.

They focus on a point in the multidimensional search

space which results to the best ﬁtness value depend-

ing on the experience of the past optimization per-

formance. This can be a local optimum, too. But

the advantage of the metaheuristic is to ﬁnd an ade-

quate solution of a multidimensional continuous op-

timization problem in reasonable time (Talbi, 2009).

This performance depends on the conﬁguration of

the metaheuristics and is an important fact of using

metaheuristics. One group of metaheuristics are the

population based metaheuristics. (Talbi, 2009) de-

ﬁnes population-based metaheuristics as nature in-

spired heuristics which handle more than one solution

at a time. With every iteration all solutions are re-

computed based on the experience of the whole pop-

ulation. Examples of population-based metaheuris-

tics are Genetic Algorithms which are an instance of

Evolutionary Algortihms, Ant Colony Optimization

and Particle Swarm Optimization. Different kinds of

metaheuristics exhibit varying performance on a spe-

ciﬁc kinds of problem types. They differ w.r.t. the

optimization speed and the solution quality. A meta-

heuristic’s performance is based on their conﬁgura-

tion. Finding a good parameter set is a non-trivial task

and often based on a priori knowledge about the ob-

jective function and the problem. Setting up a meta-

heuristic with standard parameter sets lets the opti-

mization ﬁnd a decent solution but using a parameter

set which is adapted to the speciﬁc objective function

might even lead to better results. In this paper we

focus on PSO and try to ﬁnd features characterizing

the objective function in order to select an adequate

parameter conﬁguration for this metaheuristic. The

optimization behavior of the particles is based on the

objective function and we try identify relevant infor-

mation about the function. In the following section

we give a brief introduction to particle swarm opti-

mization.

2.1 Particle Swarm Optimization

Particle Swarm Optimization (PSO) is inspired by

the social behavior of ﬂocks of birds and shoals of

ﬁsh. A number of simple entities, the particles, are

placed in the domain of deﬁnition of some function

or problem. The ﬁtness (the value of the objective

function) of each particle is evaluated at its current

location. The movement of each particle is deter-

mined by its own ﬁtness and the ﬁtness of particles

in its neighborhood in the swarm. PSO was ﬁrst in-

troduced in (Kennedy and Eberhart, 1995). The re-

sults of one decade of research and improvements to

the ﬁeld of PSO were recently summarized in (Brat-

ton and Kennedy, 2007), recommending standards for

comparing different PSO methods. Our deﬁnition is

based on (Bratton and Kennedy, 2007). We aim at

continuous optimization problems in a search space

S deﬁned over the ﬁnite set of continuous decision

variables X

, X

, . . . , X

. Given the set Ω of conditions

to the decision variables and the objective function

f : S → R (also called ﬁtness function) the goal is to

determine an element s

∗

∈ S that satisﬁes Ω and for

which f (s

∗

) ≤ f (s), ∀s ∈ S holds. f (s

∗

) is called a

global optimum.

Given a ﬁtness function f and a search space S the

standard PSO initializes a set of particles, the swarm.

In a D-dimensional search space S each particle P

consists of three D-dimensional vectors: its position

= (x

, x

, . . . , x

), the best position the particle

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

visited in the past p

= (p

, p

, . . . , p

) (particle

best) and a velocity v

= (v

, v

, . . . , v

). Usually

the position is initialized uniformly distributed over S

and the velocity is also uniformly distributed depend-

ing on the size of S. The movement of each particle

takes place in discrete steps using an update function.

In order to calculate the update of a particle we need

a supplementary vector g = (g

, g

, . . . , g

) (global

best), the best position of a particle in its neighbor-

hood. The update function, called inertia weight, con-

sists of two parts. The new velocity of a particle P

calculated for each dimension d = 1, 2, . . . , D:

new

= w ·v

+ c

−x

) + c

−x

)

(1)

then the position is updated: x

new

= x

+ v

new

. The

new velocity depends on the global best (g

), particle

best (p

) and the old velocity (v

) which is weighted

by the inertia weight w. The parameters c

and c

pro-

vide the possibility to determine how strong a particle

is attracted by the global and the particle best. The

random vectors ε

and ε

are uniformly distributed

over [0, 1)

and produce the random movements of

the swarm.

2.2 Algorithm Conﬁguration Problem

The general problem of conﬁguring algorithms (algo-

rithm conﬁguration problem) is deﬁned by Hutter et

al. (Hutter et al., 2007) as ﬁnding the best tuple θ

out of all possible conﬁgurations Θ (θ ∈ Θ). θ rep-

resents a tuple with a concrete assignment of values

for the parameter of an algorithm. Applied to meta-

heurisitcs the conﬁguration of the algorithm parame-

ters for a speciﬁc problem inﬂuences the behavior of

the optimization process. Different parameter settings

exhibit different performances at solving a problem.

The problem to conﬁgure metaheuristics is a super

ordinate problem and is analyzed for different kinds

of metaheuristics. In PSO the convergence of the

optimization depending on different parameter set-

tings and different functions are analyzed by (Trelea,

2003), (Shi and Eberhart, 1998) and (van den Bergh

and Engelbrecht, 2002). But these approaches focus

only on the convergence of the PSO but not on func-

tion characteristics and the relationship between the

parameter conﬁguration and the function landscape.

Different approaches to solve this algorithm con-

ﬁguration problem on metaheurisitcs are introduced:

One approach is to ﬁnd sets of adequate parameters

which performs a good optimization on most different

types of objective functions. This “standard param-

eters” are evaluated on a preset of functions to ﬁnd

a parameter set which leads to global good behavior

of the metaheuristic. In PSO standard parameter sets

are presented by (Clerc and Kennedy, 2002) and (Shi

and Eberhart, 1998). Some approaches do not present

a preset of parameters but change the values of the

parameters during the runtime to get a better perfor-

mance (Pant et al., 2007).

Another approach is introduced by Leyton-Brown

et al. They try to create features which describe the

underlying problem (Leyton-Brown et al., 2002) and

generate a model predicting the right parameters de-

pending on the classiﬁcation. They introduce several

features which are grouped into nine groups. The fea-

tures include, among others, problem size statistics,

e.g. number of clauses and variables, and measures

based on different graphical representations. This

analysis is based on discrete search spaces because

on continuous search spaces it is not possible to set

adequate discrete values for the parameter conﬁgura-

tion which is needed by their appraoch.

Our problem is to conﬁgure an algorithm working

on continuous search spaces and offers inﬁnite pos-

sibilities of parameter sets. To solve this challenge

we try, similar to Leyton-Brown et al., to train a clas-

siﬁer with features of the ﬁtness function landscape

computed by observing swarm behavior. These fea-

tures are computed and combined with the best found

parameter set on the function to a training instance

(see ﬁgure 1). With a trained classiﬁer at hands we

compute the features of the objective function prior

to the start of the optimization process. The classiﬁer

– in our case a decision tree – classiﬁes the function

and selects the speciﬁc parameter set that is expected

to perform better in the optimization process than us-

ing the standard parameters. In our ﬁrst experiments,

which we understand as proof of concept, we choose

only a few functions which do not represent any spe-

ciﬁc types of function. We want to show that our

technique is able to identify functions based on the

swarm behavior provided features and thereby, select

the speciﬁc parameter conﬁguration. In order to learn

the classiﬁer which suggests the parameter conﬁgura-

tion, different function features are computed. These

features are the basis of our training instances.

3 COMPUTATION OF FUNCTION

FEATURES

Our computed features can be divided into three

groups. Each group implies a distinct way of collect-

ing information about the ﬁtness topology of the ob-

jective function from particles. The ﬁrst group Ran-

dom Probing describes features which are calculated

based on a random selection of ﬁtness values and

provides a general overview of the ﬁtness topology.

EXTRACTION OF FUNCTION FEATURES FOR AN AUTOMATIC CONFIGURATION OF PARTICLE SWARM

OPTIMIZATION

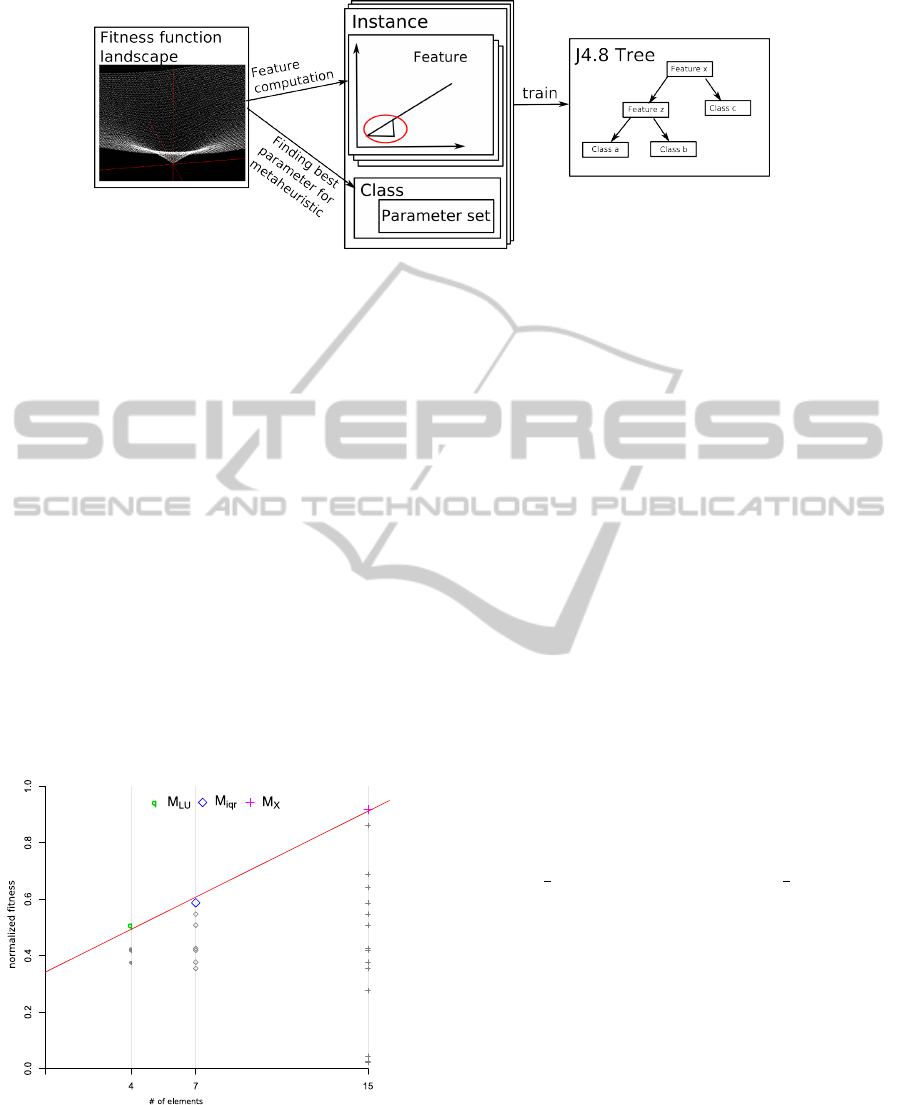
Figure 1: Process of building a classiﬁer.

Distance-based features are calculated for the second

group Incremental Probing. They reﬂect the distribu-

tion of surrounding ﬁtness values of some pivot parti-

cles. The third group of features utilizes the dynamics

of PSO to create features by using the changes of the

global best ﬁtness within a small PSO instance. The

features are scale independent, i.e., that scaling the

objective function by constants will not affect the fea-

ture values. By this we imply that a conﬁguration for

PSO leads to the same behavior on a function f as

it shows for its scaled function f

= α f + β, α > 0.

These three groups are based on each other which

means that the pivot particle for the second group is

taken from a particle of the ﬁrst group to reduce the

computing time. Important for all these features are

the number of evaluations of the objective function.

The feature computation should be only a small part

of the whole optimization computation time.

Figure 2: Example of a random probing with the comutation

of µ

RP.Max

3.1 Random Probing

Random Probing deﬁnes features that are calculated

based on a set of k = 100 random particle positions

which are within the initialization range of the ob-

jective function (100 particles to get a short but ad-

equate description about the function window). Prob-

ing the objective function results in a distribution of

ﬁtness values which is used to extract three features.

Trivial characteristics like mean and standard devi-

ation cannot be used as features since they are not

scale independent. That means, they will change their

value if the function is scaled by constants. In or-

der to create reliable features, the ﬁtness values of all

points are evaluated and three sets of particles (includ-

ing their evaluation values) are created based upon

these values. The ﬁrst set is denoted M

and con-

tains all ﬁtness values of the randomly selected points.

The quartiles for the distribution of the ﬁtness val-

ues are computed and the values between the upper

or lower quartile are joined into the second set. This

set is denoted M

iqr

. The third set M

consists of the

ﬁtness values which are between a lower and upper

boundary L and U. These boundaries are deﬁned by

L = Q

−Q

) and U = Q

−Q

)

where Q

denotes the median and Q

, Q

denote

the lower and upper quartile of M

. For each set

⊃ M

iqr

⊃ M

the number of elements is deter-

mined.

The feature Random Probing Min µ

RP.Min

is cal-

culated based on the linear model that ﬁts the rela-

tionship between the number of values and the min-

imum ﬁtness values in each set. The straight line of

the model is divided by the interquartile range of M

Similar to this the feature Random Probing Max is

based on the slope of the straight line that describes

the relationship of the number of elements and the

maximum value of each set M

⊃ M

iqr

⊃ M

(see

ﬁgure 2). The slope divided by the interquartile range

of M

denoted by µ

RP.Max

is the second feature of

this group. Finally, for the feature Random Probing

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Range denoted by µ

RP.Range

the spread, that is the

difference between the maximum and the minimum

value, in each set is computed. As for the other fea-

tures the slope is divided by the interquartile range of

. All features of this group are computed based on

the ﬁtness values of the randomly selected points. For

each point the objective function is evaluated once,

hence, k = 100 evaluations are necessary for Random

Probing.

●

● ●

−− εε x

++ εε

−− εε x

++ εε

●

x' ∈∈ M

εε

((x))

||x −− x'|| == εε||x −− x'|| ≤≤ εε

Figure 3: Example of an incremental group in a 2 dimen-

sional space.

3.2 Incremental Probing

In contrast to the features of the previous group, In-

cremental Probing is computed by the ﬁtness values

of the particle positions which are located in a deﬁned

distance to a pivotal element which we choose from

the feature group above. In order to calculate the rele-

vant ﬁtness values, the position of a randomly selected

pivot element is consecutively shifted into one dimen-

sion. The distance is given by an increment ε > 0

which shifts the position of the pivot element in both

directions of the dimension. In each dimension i In-

cremental Probing considers two points (see ﬁgure 3

for a 2 dimensonal example). For a given pivot ele-

ment x = (x

, . . . x

) and a given increment ε > 0 these

posistions are determined by



−x





ε |i = j

0 |i 6= j

(2)

where j, i ≤ n. The increment ε is deﬁned rela-

tively to the domain. For instance, in a restricted n-

dimensional domain A = I

×. . . ×I

, where the in-

terval I

= [a

, b

] deﬁnes the valid subspace, the in-

crement is applied as ε ·

−a

100

. For each dimension

the position of the pivot element is shifted into two

directions. This leads to a set of 2n + 1 points includ-

ing the pivot element. The ﬁtness value of each valid

point is calculated and these ﬁtness values are used

for the extraction of objective features.

In this group

of features, nine features are created with the use of

three increments of ε

= 1, ε

= 2 and ε

= 5. Let n

be the dimension of the domain, then 2n + 1 evalua-

tions are required to calculate the ﬁtness values of the

relevant points. Since three increments are used there

are (3 ×2n) + 1 evaluations required to calculate the

features of Incremental Probing.

The features Incremental Min, Incremental

Max and Incremental Range are computed similar

to the features of Random Probing. For each incre-

ment the minimum, maximum and the spread of the

ﬁtness values are computed. Incremental Min de-

scribes the relationship of the minimum and the cor-

responding increment. There are two subtypes for

this feature. µ

IP.Min

is divided by the slope of the

model’s straight line by the spread of the ﬁrst incre-

ment whereas the second subtype µ

IP.MinQ

divides the

slope by the interquartile range of the ﬁrst increment.

The features Incremental Max and Incremental

Range are handled accordingly. Three additional fea-

tures are created by separately looking at the ﬁtness

values of the individual increments. The ﬁtness val-

ues of each increment is sorted in ascending order and

normalized into the interval [0, 1]. This results in a se-

quence hx

i = x

, . . . , x

and we calculate a measure

of linearity by

IP.Fit

∑

i=1



−

i −1

k −1



(3)

where ∀i < j : x

< x

3.3 Incremental Swarming

The features of Incremental Swarming use the dy-

namic behavior of PSO to extract features of the ob-

jective function. Therefore, we construct a small

swarm of two particles and initiate an optimization

run. The particles are initialized with a deﬁned dis-

tance to each other. We use a inertia PSO with param-

eter θ = (0.6221, 0.5902, 0.5902) and record the best

solution found in the ﬁrst t = 20 iterations. To get the

parameter set θ we evaluated a few parameter sets em-

pirically to ﬁnd good values which lead to a fast con-

vergence of the small swarm. The spread of the global

best ﬁtness is the difference between the ﬁrst and the

last ﬁtness value. The development of the global best

ﬁtness depends on the initial positions of the particles.

Consider a swarm which is initialized at a local opti-

mum. Once a better ﬁtness value is found, global best

In case that the point is invalid, that is it lies outside the

valid domain, the evaluation of the ﬁtness value is skipped

and the ﬁtness value of the pivot element is used instead.

EXTRACTION OF FUNCTION FEATURES FOR AN AUTOMATIC CONFIGURATION OF PARTICLE SWARM

OPTIMIZATION

0 3 6 9 12 15 18 21

〈〈g

〉〉

min

max

Figure 4: Example of an incremental swarming slope where

g describes the best ﬁtness of the actual evaluation step i.

ﬁtness will change. But this may not happen in the

few iterations that are observed. Therefore the swarm

is initialized by a pivot element chosen from a set of

evaluated points. Incremental Swarming considers a

set of k = 100 evaluated solutions and the position

which evaluates to the worst ﬁtness value is chosen as

pivot element. This is important because if we choose

a pivot element randomly, it is possible to ﬁnd a lo-

cal optimum and the behavior of the swarm results

in no movement. The other particle is initialized in

a deﬁned distance to the pivot element. Similarly to

Incremental Probing we use increments to deﬁne the

distance between the particles. The increment values

= 1, ε

= 2, ε

= 5 and ε

= 10 are used to create

20 features. For each increment the feature Swarming

Slope describes the development of the global best

ﬁtness as a linear model that ﬁts the relationship be-

tween the iteration and the global best ﬁtness value

(see ﬁgure 4). For the feature µ

IS.Slope

the slope of the

straight line is divided by the spread of the global best

ﬁtness. Swarming Max Slope describes the greatest

change of the global best ﬁtness value between two

successive iterations. For normalization the value of

IS.Max

is divided by the spread of the global best ﬁt-

ness. The other three features, which are computed

for each increment, are Swarming Delta Lin µ

IS.Lin

Swarming Delta Phi µ

IS.Phi

, and Swarming Delta

Sgm µ

IS.Sgm

. They describe to what degree the ob-

served development of the global best ﬁtness value

differs from sequences that represent idealistic de-

velopments. Swarming Delta Lin implies a mea-

sure of linearity, thus quantiﬁes how much the ob-

served development differs from a linear decrease of

the global best ﬁtness. Let hx

i= x

, . . . , x

denote the

observed sequence of the global best ﬁtness value. We

compute this feature with equation 4.

IS.Lin

∑

i=0



−

t −i + 1

t −1



(4)

Similarly we create two additional ideal sequences

and compute the features µ

IS.Phi

and µ

IS.Sgm

by the

equations 5–6:

IS.Phi

∑

i=0



−φ

i−1



(5)

IS.Sgm

∑

i=0



−

1 + exp

(i−1)φ



(6)

where φ =

√

. The factor φ was selected in order

to mediate between a linear and an exponential devel-

oping. The development of the global best ﬁtness is

used to calculate the features of Incremental Swarm-

ing. The pivot element for the initialization of the

swarm is chosen from a set of k solutions and since

the swarm of m = 2 particles is applied for t = 20 it-

erations, overall there are k + m + mt evaluations of

the objective function. We choose the pivot element

from the set M

which was created for the features of

Random Probing. By this we reduce the number of

additional evaluation to m + mt = 42.

4 EVALUATION

In this section we evaluate our features and build a

classiﬁer which computes speciﬁc parameter sets for

the Particle Swarm Optimization on a speciﬁc func-

tion. This optimization should have a better perfor-

mance compared to the PSO on the same function

with standard parameter set.

4.1 Experimental Setup

We choose 7 test functions out of the suggested

test function pool from (Bratton and Kennedy, 2007)

and stop computing the ﬁtness function after 300000

times. With our swarm size of 30 the number of

epochs is consequently set to 10000. We deﬁne a run

as a parameter set which is tested 90 times with a ﬁ-

nite set of different seed values in order to get mean-

ingful results. As topology of the swarm gbest is used.

The initialization of the particle is in a deﬁned square

of the search space (see table 1). Before we start to

train our classiﬁer with the features we have to create

the classes that represent speciﬁc parameter sets with

a high quality of the optimization performance.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Table 1: Overview of the function pool and the initialization areas.

Function Optimum Domain Initialization

Ackley x

= 0 [−32, 32]

[16, 32]

Gen. Schwefel x

= 420.9687 [−500, 500]

[−500, −250]

Griewank x

= 0 [−600, 600]

[300, 600]

Rastrigin x

= 0 [−5.12, 5.12]

[2.56, 5.12]

Rosenbrock x

= 1 [−30, 30]

[15, 30]

Schwefel x

= 0 [−100, 100]

[50, 100]

Sphere x

= 0 [−100, 100]

[50, 100]

Figure 5: Parameter sets in the conﬁguration space.

4.2 Finding the Best Parameter

In order to ﬁnd the best parameter set for each func-

tion (see table 1), we start an extensive search with

respect to the continuous values. We try to focus on

real values with a precision of four decimal places.

The standard parameter set for PSO is ω = (W,C

)

with W = 0.72984 and C

= C

= 1.4962. For the

extensive examination of parameters we take into ac-

count the intervals W ∈[0, 1] and C

∈[0, 2.5]. We

create a sequence between this interval values based

on the standard value with a exponential factor of

(

√

)

where x indicates the sequence number. We

calculate 13 and 23 sequence values around the stan-

dard value and obtain a sequence of values between

the intervals. Depending on the exponential factor

the values close by the standard values have a lower

distance to each other than the values closer to the

borders of the interval. In ﬁgure 5 our conﬁguration

space of the extensive search is plotted. With all pos-

sible combinations of the single parameter values we

examine 13 ×23 ×23 = 6877 different parameter sets

and test each of them for every function 90 times.

As described above, we analyze the data of the

extensive search by comparing the results of each

conﬁguration’s optimization process on a function.

We choose the best parameter sets for every func-

tion with respect to the best performance. The best

performance is determined by the best ﬁtness value,

the mean ﬁtness value of all 90 optimization pro-

cesses and the distance to the nine other best perfor-

mances within this 90 processes. This is essential be-

cause a good solution and a high distance to the other

run results let this one run be an outlier. Figure 6

shows an example of a sorted sequence of the mean

value of all parameter sets we tested on the “Ackley”-

function. We compare the results of the speciﬁc pa-

rameter sets with the standard parameter set of (Brat-

ton and Kennedy, 2007) using our PSO implementa-

tion, and get a signiﬁcantly better result (or the same

if we found the global optimum) on gbest for all func-

tions with the selected parameter sets. Table 2 shows

our results for the speciﬁc parameters for the differ-

ent functions (300000 evaluations + 30000 evalua-

tions for feature computation; denoted as “speciﬁc”),

the same parameter set subtracting one percent eval-

uations for the feature computation (to demonstrate if

we used this one percent of computation time to ex-

tract the features, i.e., a total of 300000 evaluations;

“speciﬁc

∗

”) and the comparison to the standard pa-

rameter set included in our code. Additionally, the

comparison to the results of the original paper of Brat-

ton and Kennedy is included in the table.

The extensive search shows that the best speciﬁc

parameter sets for the functions Gen. Schwefel and

Rastrigin is comparable. The same effect is also sup-

ported by the features of both objective functions.

This denotes that both functions are assigned the same

class in our classiﬁer. All the speciﬁc parameter sets

are the base of our classes for each function. With the

identiﬁed classes and the computed set of features for

each function we can train the classiﬁer.

EXTRACTION OF FUNCTION FEATURES FOR AN AUTOMATIC CONFIGURATION OF PARTICLE SWARM

OPTIMIZATION

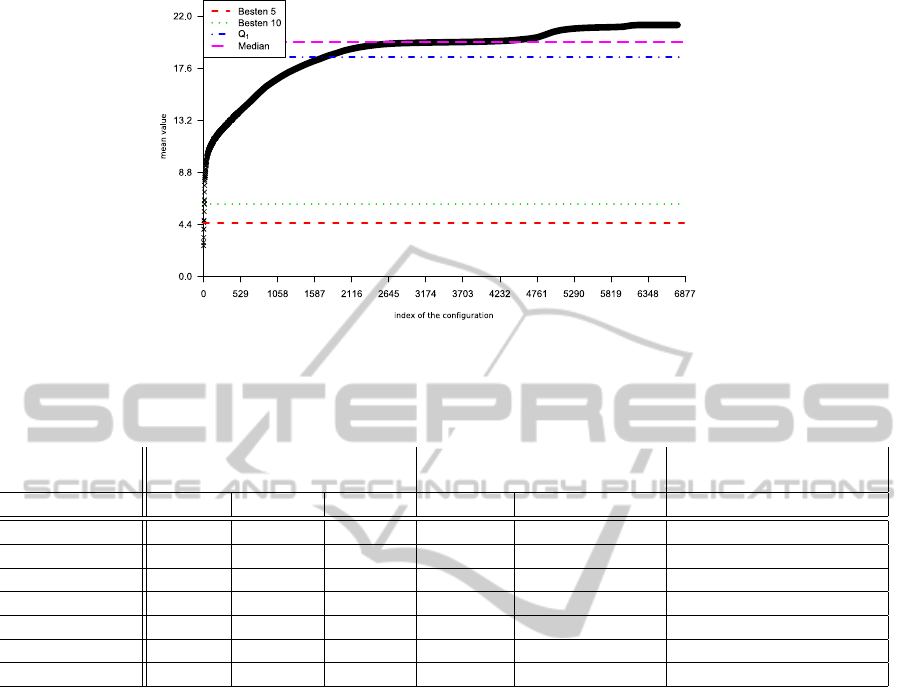
Figure 6: Sorted Set the Mean Value of all Parameterset Results.

Table 2: Comparison of the standard parameter set against the speciﬁc best parameter set;

∗

denotes the optimization with

9900 iterations, i.e., 297000 function evaluations.

Tests Reference in (Bratton and

Kennedy, 2007)

Best parameter set

Function speciﬁc speciﬁc

∗

standard gbest lbest (W,C

)

Ackley 2.58 2.62 18.34 17.6628 17.5891 (0.7893,0.3647, 2.3541)

Gen. Schwefel 2154 2155 3794 3508 3360 (0.7893,2.4098, 0.3647)

Griewank 0.0135 0.0135 0.0395 0.0308 0.0009 (0.6778, 2.1142, 1.3503)

Rastrigin 6.12 6.12 169.9 140.4876 144.8155 (0.7893,2.4098, 0.3647)

Rosenbrock 0.851 0.86 4.298 8.1579 12.6648 (0.7123,1.8782, 0.5902)

Schwefel 0 0 0 0 0.1259 more than one set

Sphere 0 0 0 0 0 more than one set

4.3 Learning and Classiﬁcation

As classiﬁer we use a C4.5 decision tree. In our

implementation we use WEKA’s J4.8 implementa-

tion (Witten and Frank, 2005). As learning input we

compute 300 independent instances for each function.

Each instance consists of 32 function features. The

decision tree is created based upon the training data

and evaluated by stratiﬁed 10-fold cross-validation

(repeated 100 times). Based on the results of the ex-

tensive search we merge the classes for the objectives

Gen. Schwefel and Rastrigin into one class. These

functions share the same speciﬁc parameter set, i.e.,

the same parameter conﬁguration performs best for

both functions. Upon these six distinct classes we

evaluate the model with cross validation. The mean

accuracy of the 100 repetitions is 84.32% with a stan-

dard deviation of 0.29. Table 3 shows the confusion

matrix of a sample classiﬁcation. As it can be seen,

there are 1769 of 2100 instances classiﬁed correctly

(this means 15.76 percent of the instances are mis-

classiﬁed). The instances of the functions Ackley

and Schwefel are classiﬁed correctly with an accu-

racy of 99.7 percent, that is only one instance of these

classes is misclassiﬁed. The class for Gen. Schwefel

and Rastrigin has an accuracy of 97.2 percent. The

class Rosenbrock has a slightly lower accuracy, but

still only 5.7 percent of its members are misclassi-

ﬁed. The high number of incorrect instances is es-

sentially due to the inability of the model to separate

the functions Sphere and Griewank. The majority of

the misclassiﬁed instances, 306 of 331, are instances

of the Griewank or Sphere class that are classiﬁed as

the other class.

4.4 Computing Effort

Computing the features is based on the evaluated ﬁt-

ness value of speciﬁc positions in the search space.

We restrict this calculation to 3000 which means one

percent of the whole optimization process in our set-

ting. To be comparable to the benchmark of Bratton

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

Table 3: Confusion matrix of the cross validation.

classiﬁed as Accuracy Precision

class Ack. Grie. G.S./R. Rosen. Schwe. Sphe. percent percent

Ackley 299 1 99.7 99.7

Griewank 116 1 183 38.7 48.1

Gen.Schwe./Rast. 1 1 583 13 2 97.2 97.2

Rosenbrock 15 283 1 1 94.3 95.3

Schwefel 1 299 99.7 99.0

Sphere 123 1 176 58.7 48.9

and Kennedy we run the optimization for the spe-

ciﬁc parameter conﬁguration for 9900 iterations lead-

ing to only 297000 ﬁtness computations. We com-

pare our results of the optimization with 10000 itera-

tions to the optimization with 9900 iterations and get

quite the same results as shown in table 2 (speciﬁc vs.

speciﬁc

∗

). The comparison shows minor differences

in the magnitude of one percent.

5 DISCUSSION AND FUTURE

WORK

In this paper we describe an approach to training

a classiﬁer which uses function features in order to

select a better parameter conﬁguration for Particle

Swarm Optimization. We show how we compute the

features for speciﬁc functions and describe how we

get the classes of parameter sets. We include the

trained classiﬁer and evaluate the parameter conﬁg-

uration against a Particle Swarm Optimization with

standard conﬁguration. Our experiments demonstrate

that we are able to classify different functions on ba-

sis of a few ﬁtness evaluations and get a parameter

set which leads the PSO to a signiﬁcantly better opti-

mization performance in comparison to a standard pa-

rameter set. Statistical tests (t-Tests with α = 0.05) in-

dicate better results for the functions where the global

optimum has not been found in both settings.

The next steps are to involve all possible conﬁgu-

rations of the PSO for example the swarm size or the

neighborhood topology. These parameters are not in-

volved in our approach because we based this work

on the benchmark approach of (Bratton and Kennedy,

2007). The behavior of the swarm changes signiﬁ-

cantly if another neighborhood is chosen. To increase

the size of the swarm is another task we will focus

in future. Depending on the swarm size different pa-

rameter sets leads to the best optimization process.

An idea is to create an abstract class of parameter

sets which include different sets of predeﬁned swarm

sizes.

In order to get more information about the perfor-

mance of our approach it would be interesting to al-

locate a ﬁxed percentage of the whole evaluations for

feature computation (e.g., 1%). In this case it would

be interesting to examine the quality of the result if

not all feature or features of minor quality were com-

puted.

Another extension is to deﬁne typical mathematical

function types to integrate not only one function as

class but a few functions combined under a simi-

lar type of functions to get a general set of parame-

ters. This might lead to a better generalization for the

learned classiﬁer. The problem of this task is to ﬁnd a

general problem class which deﬁnes typical kinds of

mathematical functions.

REFERENCES

Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).

Swarm Intelligence: From Natural to Artiﬁcial Sys-

tems. Oxford University Press, USA, 1 edition.

Bratton, D. and Kennedy, J. (2007). Deﬁning a standard

for particle swarm optimization. Swarm Intelligence

Symposium, pages 120–127.

Clerc, M. and Kennedy, J. (2002). The particle swarm

- explosion, stability, and convergence in a multidi-

mensional complex space. Evolutionary Computa-

tion, IEEE Transactions on, 6(1):58–73.

Eberhart, R. and Kennedy, J. (1995). A new optimizer us-

ing part swarm theory. Proceedings of the Sixth Inter-

national Symposium on Micro Maschine and Human

Science, pages 39–43.

Hoos, H. and St

utzle, T. (2004). Stochastic Local Search:

Foundations & Applications. Morgan Kaufmann Pub-

lishers Inc., San Francisco, CA, USA.

Hutter, F., Hoos, H. H., and Stutzle, T. (2007). Automatic

algorithm conﬁguration based on local search. In Pro-

ceedings of the Twenty-Second Conference on Artiﬁ-

cal Intelligence, (AAAI ’07), pages 1152–1157.

Kennedy, J. and Eberhart, R. (1995). Particle swarm op-

timization. Proceedings of the 1995 IEEE Interna-

tional Conference on Neural Network (Perth, Aus-

tralia), pages 1942–1948.

EXTRACTION OF FUNCTION FEATURES FOR AN AUTOMATIC CONFIGURATION OF PARTICLE SWARM

OPTIMIZATION

Leyton-Brown, K., Nudelman, E., and Shoham, Y. (2002).

Learning the empirical hardness of optimization prob-

lems: The case of combinatorial auctions. Principles

and Practice of Constraint Programming (CP ’02),

pages 91–100.

Pant, M., Thangaraj, R., and Singh, V. P. (2007). Parti-

cle swarm optimization using gaussian inertia weight.

In International Conference on Conference on Com-

putational Intelligence and Multimedia Applications,

volume 1, pages 97–102.

Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-

ing. San Mateo, CA. Morgan Kaufmann.

Shi, Y. and Eberhart, R. C. (1998). Parameter selection in

particle swarm optimization. In Proceedings of the 7th

International Conference on Evolutionary Program-

ming VII, (EP ’98), pages 591–600, London, UK.

Springer-Verlag.

Talbi, E.-G. (2009). Metaheuristics: From design to imple-

mentation. Wiley, Hoboken, NJ.

Trelea, I. C. (2003). The particle swarm optimization algo-

rithm: convergence analysis and parameter selection.

Inf. Process. Lett., 85(6):317–325.

van den Bergh, F. and Engelbrecht, A. (2002). A new lo-

cally convergent particle swarm optimiser. Systems,

Man and Cybernetics, 2002 IEEE International Con-

ference on, 3:6 pp.

Witten, I. H. and Frank, E. (2005). Data Mining: Practi-

cal machine learning tools and techniques. Morgan

Kaufmann, San Francisco, 2nd edition.

Wolpert, D. and Macready, W. (1997). No free lunch theo-

rems for optimization. IEEE Transactions on Evolu-

tionary Computation, 1(1):67–82.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence