
ACCURATE LATENCY CHARACTERIZATION FOR VERY
LARGE ASYNCHRONOUS SPIKING NEURAL NETWORKS
Mario Salerno, Gianluca Susi and Alessandro Cristini
Institute of Electronics, Rome University at Tor Vergata, Rome, Italy
Keywords: Neuron, Spiking Neural Network (SNN), Latency, Event-driven, Plasticity, Threshold, Neuromorphic,
Neuronal group selection.
Abstract: The simulation problem of very large fully asynchronous Spiking Neural Networks is considered in this
paper. To this purpose, a preliminary accurate analysis of the latency time is made, applying classical
modelling methods to single neurons. The latency characterization is then used to propose a simplified
model, able to simulate large neural networks. On this basis, networks, with up to 100,000 neurons for more
than 100,000 spikes, can be simulated in a quite short time with a simple MATLAB program. Plasticity
algorithms are also applied to emulate interesting global effects as the Neuronal Group Selection.
1 INTRODUCTION
A significant class of simulated neuromorphic
systems is represented by Spiking Neural Networks
(SNN), in which the neural activity consists of
spiking events generated by firing neurons (E. M.
Izhikevich, J. A. Gally, G. M. Edelman, 2004), (W.
Maas, 1997). In order to consider realistic models,
the simulation of the inner dynamics of the neurons
can be very complex and time consuming (E. M.
Izhikevich, 2004). Indeed, accurate neuron models
consist of complex systems of non-linear differential
equations, so that any actual simulation is
computationally convenient only in the case of quite
small networks. On the other hand, only in the case
of large networks, a number of interesting global
effects can be investigated, as the well known
Neuronal Group Selection, introduced by Edelman
(G. M. Edelman, 1987). In order to consider the
simulation of large networks, it is important to
introduce simplified models, in which any single
neuron be able to produce a class of firing patterns
quite similar to those of the biological counterpart.
In this paper, a proper SNN model will be
introduced, based on some fundamental properties of
neurons. The proposed model is able to simulate
large neuromorphic maps, up to 100,000 neurons.
A basic problem to realize realistic SNN
concerns the apparently random times of arrival of
the synaptic signals (G.L. Gernstein, B. Mandelbrot,
1964). Many methods have been proposed in the
technical literature in order to properly
desynchronizing the spike sequences; some of these
consider transit delay times along axons or synapses
(E. M. Izhikevich, 2006), (S. Boudkkazi, E. Carlier,
N. Ankri, O. Caillard, P. Giraud, L. Fronzaroli-
Molinieres and D. Debanne, 2007). A different
approach introduces the spike latency as a neuron
property depending on the inner dynamics (E. M.
Izhikevich, 2007). Thus, the firing effect is not
instantaneous, as it occurs after a proper delay time
which is different in various cases. In this work, we
will suppose this kind of desynchronization as the
most effective for SNN simulation.
Spike latency appears as intrinsic continuous
time delay. Therefore, very little sampling times
should be used to carry out accurate simulations.
However, as sampling times grow down, simulation
processes become more time consuming, and only
short spike sequences can be emulated. The use of
the event-driven approach can overcome this
difficulty (D’Haene, B. Schrauwen, J. V.
Campenhout and D. Stroobandt, 2009), since
continuous time delays can be used and the
simulation can easily proceed to large sequence of
spikes. Indeed, simulations of more than 100,000
spikes are possible by this method in a quite short
computing time.
In the proposed model, classical learning
algorithms can easily be applied in order to get
proper adjustment of the synaptic weights. In such a
116
Salerno M., Susi G. and Cristini A..
ACCURATE LATENCY CHARACTERIZATION FOR VERY LARGE ASYNCHRONOUS SPIKING NEURAL NETWORKS.
DOI: 10.5220/0003134601160124
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 116-124
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

way, adaptive neural networks can be implemented
in which proper plasticity rules are active. In
presence of input signals, the simulation of the
whole network shows the selection of neural groups
in which the activity appears very high, while it
remains at a quite low level in the regions among
different groups. This auto-confinement property of
the network activity seems to remain stable, even
when the considered input is terminated.
The paper is organized as follows: description
and simulation of some basic properties of the
neuron, such as threshold and latency; introduction
of the simplified model on the basis of the previous
analysis, description of the network structure,
plasticity algorithm, input structure, simulation
results and performance tests.
2 LATENCY
CHARACTERIZATION
Different kinds of neurons can be considered in
nature, with special and peculiar properties (S.
Ramon y Cajal, 1909-1911). On the other hand,
many models have been introduced and compared in
terms of biological plausibility and computational
cost. Antipodes are the Integrated and Fire (L.
Lapicque, 1907) and the Hodgkin-Huxley Model
(A.L. Hodgkin, A.F. Huxley, 1952), the first one
characterized by low computational cost and low
fidelity, while the second is a quite complete
representation of the real case.
In the latter case, the model consists of four
differential equations describing membrane
potential, activation of Na+ and K+ currents, and
inactivation of Na+ current (E. M. Izhikevich, 2007).
From an electrochemical point of view, the neuron
can be characterized by its membrane potential V
m
.
In the simulation starting case, the neuron lies in
its resting state, i.e. V
m
= V
rest
(Resting Potential),
until an external excitation is received.
The membrane potential varies by integrating the
input excitations. Since contributions from outside
are constantly added inside the neuron, a significant
accumulation of excitements may lead the neuron to
cross a threshold, called firing threshold TF (E. M.
Izhikevich, 2007), so that an output spike can be
generated.
However, the output spike is not immediately
produced, but after a proper delay time called
latency (R. FitzHugh, 1955). Thus, the latency is the
delay time between exceeding the membrane
potential threshold and the actual spike generation.
From a physiological point of view, such a delay
time is usually attributed to the slow charging of the
dendritic tree, as well as to the action of the A-
current, namely the voltage-gated transient K+
current with fast activation and slow inactivation.
The current activates quickly in response to a
depolarization and prevents the neuron from
immediate firing. With time, however, the A-current
inactivates and eventually allows firing (E. M.
Izhikevich, 2007). This phenomenon is affected by
the amplitudes and widths of the input stimuli and
thus rich dynamics of latency can be observed,
making it very interesting for the global network
desynchronization.
It is quite evident that latency concept strictly
depends on an exact definition of the threshold level.
However, strictly speaking, the true threshold is not
a fixed value, as it depends on the previous activities
of the neuron, as shown by the Hodgkin-Huxley
equations (A.L. Hodgkin, A.F. Huxley, 1952).
Indeed, a neuron is similar to a dynamical system, in
which any actual state depends on the previous ones.
The first work addressing the threshold from a
mathematical point of view was FitzHugh (R.
FitzHugh, 1955), who defined the Quasi Threshold
Phenomenon (QTP). A finite maximum latency is
defined, but neither a true discontinuity in response
nor an exact threshold level are considered. Indeed,
with reference to the squid giant axon model, it has
been pointed out that the membrane fluctuations for
experimental observations or insufficient accuracy
for the simulators, make not possible to establish an
exact value of the threshold. To this purpose, in
figures 1a and 1b, it is shown that the neuron
behaviour is very sensitive with respect to small
variations of the excitation current.
Nevertheless, in the present work, an appreciable
maximum value of latency will be used. This value
is determined by simulation and applied to establish
a reference threshold point. When the membrane
potential becomes greater than the threshold, the
latency appears as a function of V
m
. To this purpose,
proper simulations have been carried out for single
neurons.
3 SINGLE NEURON
SIMULATIONS
Significant latency properties will be analysed in this
section. To this purpose, the NEURON Simulation
Environment (http://www.neuron.yale. edu/neuron/)
has been used, a tool for quick development of
ACCURATE LATENCY CHARACTERIZATION FOR VERY LARGE ASYNCHRONOUS SPIKING NEURAL
NETWORKS
117

Figure1: Change of membrane potential, caused by two
current pulses of 0.01 ms applied to the initial resting state
at t = 0. The amplitudes are 0.64523 nA (fig. 1a) and
0.64524 nA (fig. 1b). The behaviours, obtained by the
simulator NEURON, appear very sensitive with respect to
the current amplitude and justify the name “All-Or-None
law”, adopted in neuroscience in these cases.
Figure 2: Instantaneous variation of ΔV
m
for an impulsive
current injected I
ext
.
realistic models for single neurons, on the basis of
Hodgkin-Huxley equations.
In the field over the threshold level, the latency
can directly be related to input current pulses,
received as stimuli from spikes generated by afferent
neurons. Since the instantaneous variations of
membrane potential (
ΔV
m
) appear almost linear
with respect to the related current pulses, the latency
can also be represented as a function of the
membrane potential. Note that, starting from the
resting state (Vrest = -65 mV), an excitatory pulse of
1 nA (0.01 ms time width) corresponds to
ΔV
m
= 10
mV .
Three significant cases have been simulated,
using the integration step of 0.00125 ms and the
current pulse width of 0.01 ms.
α) Case of Single Excitatory Current Pulses
Starting from the resting state, an input current pulse
of proper amplitude, able to cause output spike after
a proper latency time, has been applied. Simulating a
set of examples, with current pulses in the range [
0.64524 ÷ 10 ] nA , the latency as a function of the
pulse amplitude, or else of the membrane potential
V
m
, has been determined. The latency behaviour is
shown in Fig. 3, in which it appears decreasing, with
an almost hyperbolic shape. The threshold level
corresponds to the pulse amplitude equal to 0.64524
nA , with the maximum latency of 10.6313 ms .
Pulses with less amplitudes are under the threshold
level, so that no output spikes are more obtained in
these cases.
Figure 3: Latency as a function of the membrane potential
(or else of the current amplitude Iext , equivalently).
β) Case of Two Excitatory Current Pulses
Starting from the resting state, after a first input
current pulse, able to cause an output spike, a second
pulse has been applied in the latency interval, in
order to analyse the corresponding latency speed up
in the firing process. As the first pulse is of fixed
amplitude (equal to 0.64524 nA), the overall latency
is a function of the second pulse amplitude (varying
in the range [ 0.001 ÷ 5 ] nA) and of the time interval
Δ, between the two excitatory current pulses.
In fig. 4, the behaviours of the overall latency
time, i.e. the time between the first pulse and the
output spike, in function of the second pulse
amplitude, are shown, for different values of Δ. Note
that the overall latency always decreases with the
second pulse amplitude. However, while the effect
of the second pulse is quite relevant for low values
of Δ, it becomes almost irrelevant when Δ is high,
i.e. almost equal to the value of the latency
corresponding to the first pulse only.
γ) Case of a First Excitatory and a Second
Inhibitory Current Pulse.
Starting from the resting state, after a first input
current pulse, able to cause an output spike, a second
pulse has been applied in the latency interval, after
the
time interval Δ. The second pulse is negative, so
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
118

Figure 4: Set of behaviours corresponding to excitatory-
excitatory stimuli. Each curve represents the overall
latency in function of the second stimulus amplitude, for a
fixed time interval Δ between the two stimuli. The effect is
greater in the case of low values of Δ.
that an inhibitory effect is produced. As the first
pulse is of fixed amplitude (equal to 3.0 nA, which
ensures that the membrane potential is carried quite
over the threshold), the second one is of varying
amplitude (from -0.01 nA, until it be still possible to
appreciate the output spike).
Once the second pulse is applied, the main effect
is the generation of an action potential delay
increment, caused by the inhibitor pulse. The more
the inhibitor pulse is strong, the greater the delay
resulted in the generation of action potential. In
addition, more the inhibitor pulse is timely, greater
is the latency produced. Even in this case, the overall
latency is a function of the second pulse amplitude
(fig.5). It is worth to emphasize that, as the interval
between the two pulses becomes relatively large, the
influence of the inhibitor is cancelled.
Figure 5: Set of behaviours corresponding to excitatory-
inhibitory stimulation. Each curve represents the latency in
function of the inhibitory stimulus amplitude, for a fixed
time interval Δ between the two stimuli. The latency
variation is greater in the case of low values of Δ.
4 SIMPLIFIED NEURON MODEL
IN VIEW OF LARGE NEURAL
NETWORKS
In the simplified model, a number of normalized and
simplified quantities are introduced, to represent
their physical counterpart. The membrane potential
is represented by a normalized real positive number
S , said the inner state of the neuron, defining the
value S = 0 as the resting state. The firing threshold
corresponds to the value S
0
, so that the activity of
the neuron can properly be classified, as passive
mode if S < S
0
, and active mode if S > S
0
.
In active mode, the neuron is ready to fire, and
the latency is modelled by a real positive quantity t
f
,
called time-to-fire . To this purpose, a bijective
correspondence between the state S and t
f
is
introduced, called the firing equation. A simple
choice for the normalized firing equation is the
following one:
t
f
= 1 / ( S - 1 ) , for S > S
0
(1)
In the model, t
f
is a measure of the latency, as it
represents the time interval in which the neuron
remains in the active state. Thus, time-to-fire
decreases with time and, as it gets to zero, the firing
event occurs. If the normalized firing threshold S
0
is
chosen such that
S
0
= 1 +
ε
(2)
the maximum value of time-to-fire is equal to
t
f,max
= 1 /
ε
(3)
Equation (1) is a simplified model of the
behaviour shown in section 3, fig. 3. Indeed, as the
latency is a function of the membrane potential,
time-to-fire is dependent from the state S, with a
similar shape, like a rectangular hyperbola. The
simulated and the denormalized firing equation
behaviours are compared in fig. 6.
Figure 6: Comparison between the latency behaviour and
that of the denormalized firing equation. The two
behaviours present a shape similar to a rectangular
hyperbola.
ACCURATE LATENCY CHARACTERIZATION FOR VERY LARGE ASYNCHRONOUS SPIKING NEURAL
NETWORKS
119
In a similar way, it could easily be proved that
also the behaviours shown in fig.s 4 and 5 can
correctly be modelled by the proper use of the firing
equation. Indeed, it is important to stress that
equation (1) must be applied as a bijective relation.
Thus, in the case of more input pulses, the following
steps must be considered.
a) As the appropriate first input is applied, the
neuron enters in active mode, with a proper state S
A
and a corresponding time-to-fire t
f A
.
b) According to the bijective firing equation, as
time goes on,
t
f A
decreases to the value t
f B
= t
f A
- Δ
and the corresponding inner state S
A
increases to the
new value S
B
, until the second input is received.
c) After the interval Δ, the second input is
received. It is clear that now the new state
S
B
is to be
considered. The state S
B
is now affected by the input
and, the greater is Δ (in the interval 0 < Δ <
t
f A
), the
greater the corresponding value of S
B
. Thus, the
effect of the second input pulse becomes irrelevant
for great values of Δ.
This peculiar property proves the good validity
of the proposed model.
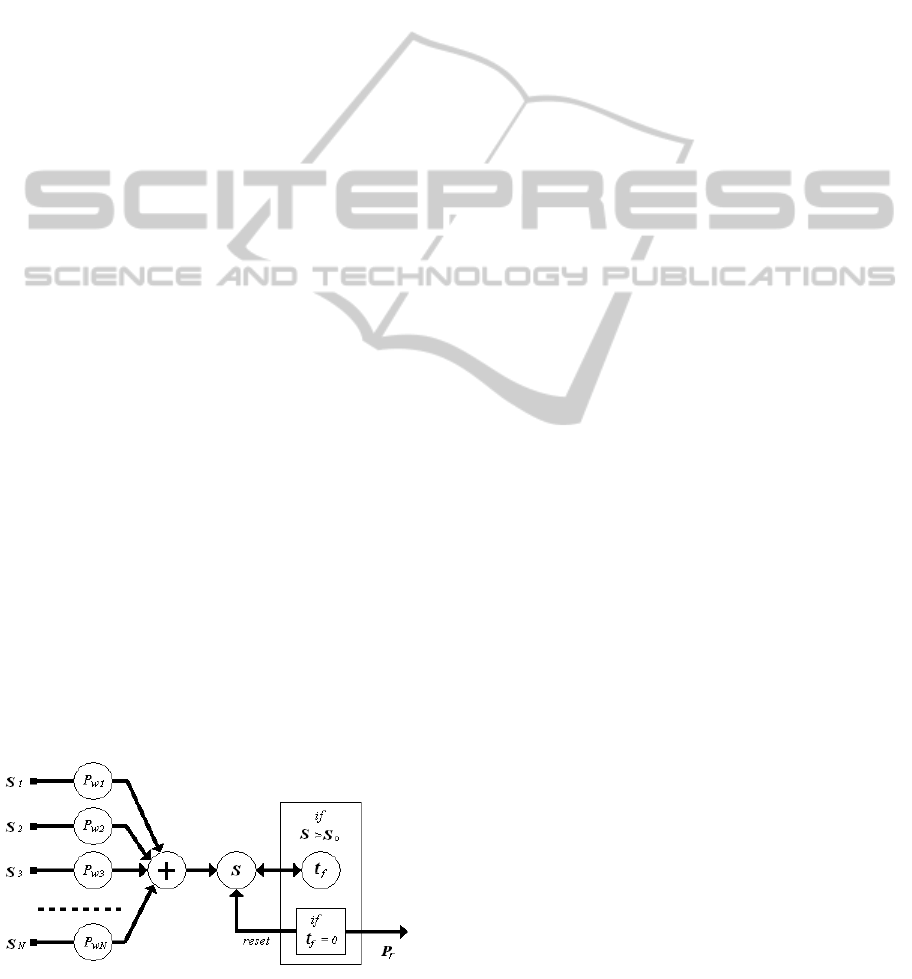
In the model, the firing event consists in the
generation of the output signal. When the firing
event occurs in a certain neuron, it is said a firing
neuron. The firing event consists of the following
steps.
A) Transmission of the firing signals through the
output synapses connected to the receiving neurons,
said burning neurons. In the proposed model, the
transmission is considered instantaneous, thus the
transmitted signals are impulses of amplitude equal
to the presynaptic weight, Pr.
B) Resetting the inner state S to the rest state S =
0.
C) For each directly connected burning neuron k,
modification of its inner state S
k
as
S
k
= S
k
+ Pr Pw
(4)
in which Pw is the related postsynaptic weight of the
considered synapse.
Figure 7: Proposed model for the neuron.
It is evident that the model introduces a
modulated delay for each firing event. This delay
strictly depends on the inner dynamics of the neuron.
Time-to-fire and firing equation are basic
concepts to make asynchronous the whole neural
network. Indeed, if the firing equation is not
introduced, and time-to-fire is always equal to zero,
the fire event would be produced exactly when the
state S becomes greater than S
0
, and this would
happen at the same time for all the neurons reaching
their active modes. Thus, the behaviour of the whole
network would be synchronous. The definition of
time-to-fire as a continuous variable let the firing
process dependent on the way by which each firing
neuron has reached its active mode.
In the classical neuromorphic systems, neural
networks are composed by excitatory and inhibitory
neurons. In our model, the presynaptic weight P
r
are
chosen positive for excitatory and negative for
inhibitory neurons.
5 NETWORK STRUCTURE
The connection map of the neurons is defined
establishing for each firing neuron (in which the
firing event is produced) the burning neurons
directly connected to it by proper synapses, through
proper postsynaptic weights. It is evident that the
difference between firing and burning neurons is
only considered to define the related synapses and
the network topology. Indeed, any neuron can be
minded either firing or burning, whether it generates
or receives a spiking signal. The whole synapse
distribution can be stored in a general N x N matrix [
P
w
] , in which N is the total number of neurons.
Each entry of this matrix represents the post-
synaptic weight corresponding to a firing vs. a
burning neuron. If such a synapse is not present, the
entry is zero, and thus, as the synaptic connection
net among neurons is usual quite not complete, the
matrix [ P
w
] will be sparse. Moreover, for large
number of neurons, the complete N x N matrix
cannot easily be stored. Thus, proper sparse matrix
technique has been applied in the simulation
program, in order to optimise the memory
requirements.
Many network topologies could be implemented
by this technique. In the proposed simulation
program, the simple case of local like connections is
considered, as in the case of Cellular Neural
Networks (L.O.Chua, L.Yang, 1988) . Each firing
neuron is directly connected to a number of burning
neurons belonging to a proper neighbourhood. The
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
120

local connection maps are shown in fig.s 8 and 9,
where grids of excitatory (en) and inhibitory (in)
neurons are indicated. The following classes of
synapse kinds are defined: s
ee
, s
ei
, s
ie
, while
synapses s
ii
are never present (the subscript e stands
for excitatory neuron, and i for inhibitory neuron).
Figure 8: Map of synapses s
ee
, and s
ie
; xn stands for
excitatory or inhibitory firing neuron, while en for
excitatory burning neurons.
As shown in the literature, greater
neighbourhood is applied for inhibitory neurons (G.
M. Edelman, 1987). Therefore, in the case of
synapses s
ei
, inhibitory burning neurons are not
neighbouring to the related excitatory firing
counterpart. Note that fig.s 8 and 9 refer to the case
of minimum neighbourhood.
Figure 9: Map of synapses s
ei
; en stands for excitatory
firing neuron, while in for inhibitory burning neurons.
6 PLASTICITY RULES
Plasticity consists in the proper variation of the post-
synaptic weights P
w
, according to the neuron
dynamics. All the P
w
weights are bounded from a
minimum to a maximum value, and are always
positive quantities. The classical Hebb rule was
proved not to be quite suitable to properly model the
complex plasticity behaviour of natural nervous
system. In this paper, three plasticity effects have
been implemented, according to (G. M. Edelman,
1987).
Exponential decay: all postsynaptic weights are
decreased to the minimum value in an exponential
way with proper time constant.
Heterosynaptic enhancement: when a burning
event occurs from a certain synapse, the
postsynaptic weight is increased to the maximum
value, in function of previous burnings on the same
neuron, in a specified time window (heterosynaptic
window) from other synapses.
Homosynaptic enhancement: when a burning
event occurs from a certain synapse, the
postsynaptic weight is increased to the maximum
value, in function of previous burnings on the same
neuron and from the same synapse, occurred in a
specified time window (homosynaptic window).
The growing rates (increase, decrease) related to
hetero and homosynaptic rules are properly chosen.
7 SIMULATION
The proposed neural paradigm has been
implemented in a simple MATLAB program. The
simulation method proceeds looking for the next
firing event occurring in the whole network. It can
be seen that the proposed model is not suitable for a
classical simulation procedure based on a specified
sampling time. Indeed, as small this sampling time is
chosen, two contiguous firing events are likely to
occur in the whole net, in a less time interval. Thus,
larger networks are simulated, smaller time intervals
can occur. Time continuity in the simulation is then
necessary, in particular for very fast dynamics. On
the other hand, the use of very little sampling times
can make very slow the simulation process.
Then, it is evident that event-driven simulation
method is quite suitable to the proposed neural
model. To this purpose, a proper matrix is
introduced in which all the active neurons are stored,
together with their time-to-fire values. Looking for
the lower time-to-fire, the next firing event is
identified in term of the firing neuron and the instant
of the event. Then, the active neuron matrix is
properly updated and the new time value is
identified in the event driven process. Therefore, the
simulation proceeds in a very fast way.
Network activity is based upon two steps.
en en en
en xn en
en en en
en en en
en xn en
en en en
in in in
in en in
in in in
in in in
in en in
in in in
ACCURATE LATENCY CHARACTERIZATION FOR VERY LARGE ASYNCHRONOUS SPIKING NEURAL
NETWORKS
121

1. Searching for the active neuron with the
minimum time-to-fire
2. Evaluation of the effects of the firing event to
all the burning neurons.
A necessary condition to maintain the activity is
that unless one neuron be active in every time. If this
is not the case, all the neurons are passive and the
activity is terminated.
Burning events can be classified in four classes.
a. Passive Burning. In this case a passive neuron
remains still passive after the burning event, i.e. the
inner state is always less than the threshold.
b. Passive to Active Burning. In this case, a
passive neuron becomes active after the burning
event, i.e. the inner state becomes greater than the
threshold, and the proper value of the time-to-fire
can be evaluated. This is possible only in the case of
excitatory firing neurons. The case α ) , analysed in
section 3, belongs to this class of burnings.
c. Active Burning. In this case an active neuron,
affected by the burning event, still remains active,
while the inner state can be increased or decreased
and the time-to-fire is properly modified. The cases
β ) and γ ), analysed in section 3, belong to this class
of burnings.
d. Active to Passive Burning. In this case an
active neuron comes back to the passive mode. This
is only possible in the case of inhibitor firing
neurons. The inner state decreases and becomes less
than the threshold. The related time-to-fire is
cancelled.
Since any firing event always makes passive the
firing neuron, the frequency of burnings of classes a)
and b) must be sufficiently high. Indeed, burnings of
class c) only modify the time evolution, and burning
of class d) reduces the global activity. On this basis,
many criteria can be introduced to evaluate the
activity level of the whole network.
A significant parameter by which the global
stability can be controlled is the presynaptic weight
P
r
which represents the firing signal amplitude for
each firing neuron in the net. Indeed, lower values of
P
r
lead to the reduction of total number of firing
neurons, up to the deadline of any activity. On the
contrary, higher values of P
r
let increase the firing
number, up to the saturation of the system. A quite
correct value of P
r
can be chosen considering the
number of synapses starting from a given firing
neuron (fan-out, f
o
). Since each firing event
produces the resetting of inner state S from S
0
(normalized threshold) to 0 , the value S
0
can be
thought distributed among all the synapses outgoing
the neuron. Thus, a useful choice is Pr = S
0
/ f
o
. This
choice was proved quite likely to guarantee the
network stability.
7.1 Input Structure
Input signals are considered quite similar to firing
spikes, though depending from external events.
Input firing sequences are connected to some
specific neurons through proper external synapses.
Thus, proper input burning neurons are chosen.
External firing sequences are multiplied by proper
postsynaptic weights in the burning process. Also
these weights are affected by the described plasticity
rules, thus the same inputs can be connected to
different burning neurons, showing different effects
in the various cases.
7.2 Simulation Tests
Several simulation tests have been carried out on the
proposed neural paradigm. In many cases, random
values for the postsynaptic weights have been
chosen as starting point for the simulation.
If proper input sequences are simulated, and if
the proposed plasticity rules are active, some
properties of the network evolution have been
verified, in particular the selection of specific neural
groups, in which the activity appears in a quite high
level, while it remains lower in the regions among
different groups. This auto-confinement property of
the network activity seems to remain stable, even if
the considered input is terminated.
As an example, we propose a neural network of
the following characteristics:
Number of excitatory neurons = 18060
number of inhibitory neurons = 2021
number of external sources = 25
The excitatory neurons are located in a
bidimensional grid. The size of the grid is 140 x 129.
Since a neighbourhood equal to 4 is chosen, a total
number of 1,608,220 postsynaptic weights is
implemented. As an initial choice, these weights
have been assigned in a random way, from a
minimum to a maximum value. In order to carry out
a network able to show an initial activity, proper
starting values for the states S have been assigned.
In this way, the initial number of active neurons was
equal to 2452.
In fig. 10, the map of the network is represented,
in which every neuron is shown as a point. Clearer
points represent neurons in the cases of lower values
of their inner states S, while darker points refer to
the cases of higher S.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
122

We present here the simulation parameters of the
network after a number of firings equal to 22518.
The normalized inner simulation time is equal to
116.5, where the number of active neurons is
reduced to 1096. The new neuron map is shown in
fig. 11, in which the activity of the network appears
not uniform, as that shown in fig. 10. Indeed, five
specific groups are now present, in which the most
of active neurons are grouped. The bounds of groups
are quite sharp and the activity in the regions among
them is near to zero.
Figure 10: Map of the neural network used in the
simulation test. Each point represents a single neuron.
Brighter points stand for low values of S , darker for
higher values. The map refers to the random initial
configuration, before processing.
Figure 11: The same map of fig. 10, after simulation. The
Neural Group Selection clearly appears.
The simulation parameters, involved in the
process from the initial map of fig. 10 to that of fig.
11, are the following ones:
Number of firing = 22,517
Number of burnings:
passive = 1,163,500
passive-to-active = 21,020
active = 568,891
active-to-passive = 1223
The parameters involved in the plasticity rules
are the following ones:
Number of etherosynaptic upgrading
= 39,469,900
Number of homosynaptic upgrading
= 2,341,430
Typical time performances of the simulation test
is about 11 minutes, on a Pentium dual core 2.5 GHz
(ram: 2GB).
8 CONCLUSIONS
Neural networks based on a very simple model have
been introduced. The model belongs to the class of
Spiking Neural Networks in which a proper
procedure has been applied to accounting for latency
times. This procedure has been validated by accurate
latency analyses, applied to single neuron activity by
simulation methods based on classical models. The
firing activity, generated in the proposed network,
appears fully asynchronous and the firing events
consist of continuous time sequences. The
simulation of the proposed network has been
implemented by an event-driven method, allowing
the possibility of simulating very large network by a
quite simple MATLAB procedure. The simulation
shows the appearance of the well known Neuronal
Group Selection, when proper input sequences and
proper plasticity rules are applied.
Future works in the field could be about the
stability analysis of the firing activity and of the
plasticity rules, in order to generate permanent
functional groups in the whole network. The results
related to the analysis of chaotic firing processes in
single groups seem also very promising.
REFERENCES
E. M. Izhikevich, J. A. Gally, G. M. Edelman, 2004:
“Spike-timing dynamics of neuronal groups”, 14:933–
944. Oxford University press.
ACCURATE LATENCY CHARACTERIZATION FOR VERY LARGE ASYNCHRONOUS SPIKING NEURAL
NETWORKS
123

W. Maas, 1997: “Networks of Spiking Neurons: The Third
Generation of Neural Network Models”. Elsevier
Science Ltd.
E. M. Izhikevich, 2004: “Which model to use for cortical
spiking neurons?” IEEE Transactions on neural
networks, Vol. 15
G. M. Edelman, 1987: “Neural Darwinism: The Theory of
Neuronal Group Selection”. Basic Books, New York.
G. L. Gernstein, B. Mandelbrot, 1964: “Random walk
models for the spike activity of a single neuron”.
Biophisical journal, Vol.4.
E. M. Izhikevich, 2006: “Polychronization: computation
with spikes”. Neural Computation 18, 18:245-282.
S. Boudkkazi, E. Carlier, N. Ankri, O. Caillard, P. Giraud,
L. Fronzaroli-Molinieres and D. Debanne, 2007:
“Release-Dependent Variations in Synaptic Latency: A
Putative Code for Short- and Long-Term Synaptic
Dynamics”.Neuron, volume 56, issue 6.
E. M. Izhikevich, 2007: “Dynamical Systems in
Neuroscience: The Geometry of Excitability and
Bursting”. The MIT press.
M. D’Haene, B. Schrauwen, J. V. Campenhout and D.
Stroobandt, 2009: “Accelerating Event-Driven
Simulation of Spiking Neurons with Multiple Synaptic
Time Constants”. Neural computation, apr. 21(4).
S. Ramon y Cajal, 1909, 1911: “Histologie du Systeme
Nerveux de l'Homme et des Vertebres, vol. I & II”.
L. Lapicque, 1907: “Recherches quantitatives sur
l’excitation électrique des nerfs traitée comme une
polarization”.
A. L. Hodgkin, A.F. Huxley, 1952: “A quantitative
description of membrane current and application to
conduction and excitation in nerve”, Journal of
Physiology, 117, 500-544.
R. FitzHugh, 1955: “Mathematical models of threshold
phenomena in the nerve membrane”. Bull.
Math.Biophysics
http://www.neuron.yale.edu/neuron/
L. O. Chua, L.Yang, 1988: “Cellular Neural Networks:
Theory”. IEEE Trans. Circuits Syst., vol. 35.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
124
