A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL

ANALYSIS

P. Carvalho, R. P. Paiva, D. Kumar, J. Ramos, S. Santos and J. Henriques

Department of Informatics Engineering, University of Coimbra, Pólo II, Coimbra, Portugal

Keywords: Non-cardiac Sound Detection, Heart Sound Segmentation, S3 Detection, S2 Split Detection, Heart Murmur,

Systolic Time Intervals.

Abstract: Cardiac auscultation is a traditional, yet highly sensitive and specific diagnosis technique for cardiovascular

diseases. We present a Matlab framework for cardiac signals processing and analysis, which includes a new

toolbox specifically designed for the main processing tasks related to heart sound analysis. Existing

frameworks for acoustic cardiac signal analysis usually limit themselves to noise contamination detection,

S1 and S2 segmentation and murmur diagnosis. Besides these operations, the proposed framework includes

algorithms developed for segmentation of the main heart sound components capable of handling situations

with high-grade murmur, S3 detection and identification, S2 split identification as well as systolic time

intervals (STI) measurement using heart sound. Methods for cardiac function parameter extraction based on

STI are also included. Most of the algorithms outlined in the paper have been extensively evaluated using

data collected from patients with several types of cardiovascular diseases under real-life conditions. The

achieved results suggest that the algorithms developed for the framework exhibit performances that are

comparable and, in most cases, surpass existing state of the art methods.

1 INTRODUCTION

Cardiovascular diseases (CVD) are the leading cause

of death worldwide. According to the European

cardiovascular disease statistics report (Allender, et

al. 2008), 44% of all deaths in men in Europe are

due to CVD, whereas the disease accounts for 54%

of all deaths in women. CVD is not solely a problem

of developed countries, quite the contrary. In fact, as

is mentioned in the WHO report on chronic diseases

(WHO, 2005), 80% of all deaths worldwide due to

chronic diseases occur in middle and low-income

countries, being CVD by far the most prevalent

chronic disease. Recent studies have shown that

premature CVD and its consequences can be largely

prevented and controlled by fostering healthy

lifestyles and by timely detection/control of

progression of the disease. For the population that

already exhibits the disease, the later is of paramount

importance since timely diagnosis usually leads to

more successful and cost effective therapies. Due to

the unprecedented aging of the world population

(Rechel et al., 2009), timely action has decisive

impact on health provision systems’ sustainability.

The first line of defense against CVD is the regular

follow-up by primary care physicians. Given the

medical, social and economical implications of

CVD, a significant research trend is observed in

science and technologies to deploy personal health

(pHealth) systems for CVD management (e.g.

Habetha, 2006). The goal of these systems is to

support physicians and patients in detecting trends

and in collecting data for clinical decision support.

In order to implement cost effective CVD

prevention strategies, pHealth systems as well as

physicians require affordable, comfortable and

highly discriminative information sources for

diagnosis. Traditionally, the electrocardiogram

(ECG) and heart sound (HS) auscultation are among

the most used signals for CVD diagnosis. These

information sources provide complementary

information: the ECG enables to assess the electrical

activity of the heart, while heart sounds provide

information on the mechanical activity of the heart

(Tavel, 1967). Other signals, such as the impedance

cardiogram (ICG) as well as the

photoplethysmogram (PPG), are less common in

daily practice or are still used mainly in research

scenarios.

151

Carvalho P., P. Paiva R., Kumar D., Ramos J., Santos S. and Henriques J..

A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS.

DOI: 10.5220/0003134701510160

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 151-160

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper we introduce a Matlab framework for

the acquisition and processing of cardiac signals.

The framework (see fig. 1) includes a general real-

time signal acquisition toolbox to interface medical

Figure 1: (top) Layer architecture of the proposed

framework. (bottom) Detailed layer architecture of the

heart sound processing toolbox.

sensor networks and a collection of signal analysis

toolboxes for the most pertinent signals to deploy

portable and non-invasive devices for CVD

diagnosis. Regarding the signal processing layer of

the framework, the focus of this paper will be to

present the algorithms developed by the team for the

HS toolbox. These include methods for noise

detection, heart sound segmentation into its main

components (S1, S2 and S3) as well as higher level

operations such as S2 split detection (important to

assess pulmonary artery pressure), regurgitation and

stenosis murmur detection and classification, and left

ventricle cardiac function assessment (systolic time

intervals, contractility and stroke volume). The

remaining toolboxes are presented elsewhere: a

description of the ECG toolbox can be found in

(Henriques et al., 2008); the ICG algorithms

implemented in the ICG toolbox are described in

(Carvalho et al., 2011), whereas the PPG toolbox is

based on the segmentation method introduced in

(Chan et al., 2007).

Heart sound is a consequence of turbulent blood

flow and vibrating cardiovascular structures, which

propagate to the chest. These vibrations typically

result from myocardial and valvular events that are

affected by the function, the hemodynamics and

electrical activity of the cardiac muscle. The later

have a direct impact on the morphological, spectral

and the timing characteristics of the main heart

sounds (S1, S2 and S3), which have been found to be

highly sensitive and specific for several important

diagnosis tasks ranging from heart valve dysfunction

(Durand & Pibarot 1995), (Abbas&Bassam, 2009) to

systolic cardiac function (Paiva et al. 2009; Tavel

1967).

Unfortunately, cardiac auscultation - the

interpretation of heart sounds - requires highly

proficient physicians. Several studies (e.g. Lam et

al., 2005) have shown that the ability of physicians

to perform cardiac auscultation is reduced and

significantly impaired as time progresses. It is

estimated that this might lead to a number of missed

diagnosis and to a high rate of unnecessary referrals

to cardiologists with a consequence of waste of

scarce resources (Pease, 2001). Hence, the existence

of signal analysis algorithms for HS to deploy

decision support systems, both for the physicians in

their clinical practice as well as to deploy pHealth

systems, are one possible solution to fully explore

this highly informative, low cost and non-invasive

information source on cardiac state.

There are few known integrated frameworks for

heart sound acquisition and processing. Most of the

existing literature is concentrated on algorithms for

elementary processing functions (most of the efforts

focus on HS segmentation and murmur

classification). An extensive review on algorithms

for heart sound analysis as well as CVD diagnosis

algorithms based on HS can be found in

(Abbas&Bassam, 2009; Durand&Pibarot, 1995;

Tavel, 1967). Rajan et al. (1998) introduce an

integrated framework for HS processing based on

Morlet wavelet bank of correlators. Their framework

tackles the problems of noise detection, S1 and S2

segmentation and murmur/click/snap classification.

Javed et al. (2006), describe a signal processing

module that includes a signal acquisition

functionality. Time-frequency processing is wavelet-

based and is limited to HS segmentation and murmur

detection. More recently, Syed et al. (2007)

introduced a framework with similar functionalities

as the one described in (Rajan et al., 1998).

Kudriavtsev et al. (2007) introduce a framework for

HS analysis based on time-frequency signatures

assessed using the Wigner-Ville distribution. This

framework enables HS segmentation, including S3

and S4 detection, as well as murmur detection. It is

observed that none of the sited frameworks include

modules for systolic time interval measurement, i.e.

the pre-ejection period (PEP) and the left ventricle

ejection time (LVET), which is related directly to the

left ventricle function. Some of these frameworks

include facilities to assess the so-called

electromechanical time interval, RS2, defined by the

ECG’s R-peak and the S2 sound; it should be noted

that RS2≈PEP+LVET. However, as was mentioned

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

152

by Oh and Tajik (2003), reduced systolic left

ventricle function will have opposite effects on PEP

and LVET, possibly cancelling each other out.

The paper is organized as follows: Section 2 outlines

the algorithms that have been developed by the team

and are integrated into the heart sound processing

toolbox. In section 3 we present and discuss results

of the main modules that comprise the toolbox.

Finally, in section 4 some main conclusions are

drawn and the main directions for future work are

outlined.

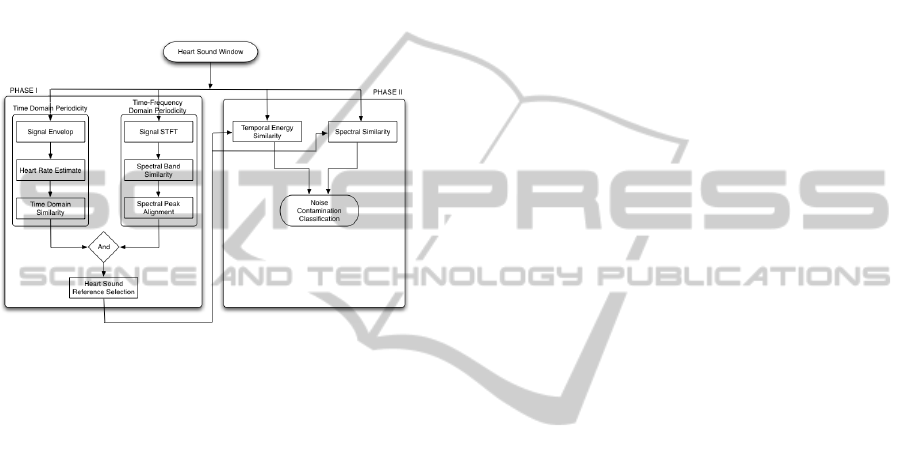
Figure 2: Noise detection algorithm.

2 HEART SOUND ANALYSIS

TOOLBOX

2.1 Noise Detection

The first step in developing a clinical application

based on HS is to exclude signal portions with noise

contaminations. Noise interference in HS might

come from internal (e.g. physiological noises) as

well as external (e.g. noises by bystander) sources

and interfere in highly complex and unpredictable

ways. These noise sources exhibit a very broad range

of spectral bands, loudness and durations. Noise

detection is tackled in the toolbox by observing that

HS are quasi-periodic signals. This characteristic

manifests itself both in the time domain as well as in

the time-frequency domain for different frequency

bands. The proposed strategy is depicted in the

flowchart in fig. 2: in phase I a non-contaminated HS

clip of one complete heart cycle is selected. This HS

will serve as a reference template for further

processing; since this selection operation is always

performed at the start of the signal acquisition

process, it ensures that the method exhibits resilience

towards auscultation site, posture changes and

changing physiological characteristics. In order to

grant that this reference template does not exhibit

noise contamination, the template is selected from

candidates that exhibit the aforementioned quasi-

periodicity characteristics. In the second phase this

template is applied to each signal window using

temporal energy and spectral similarity criteria to

check for noise contamination.

Regarding phase I, first each individual heart

beat is identified in the HS signal. If an ECG is

available, this can be obtained using the R-peaks.

Otherwise, the heart cycle limits can be estimated

from the prominent peaks (which correspond to S1

and S2) of the signal’s envelop and the heart rate

assessed from the singular value decomposition

(SVD) of the envelop of the signal. Let

(t) be the

envelop of the HS obtained using the Hilbert

transform. Let

k(wT) = [y(wT), …, y((w+1)T)] and

S(T) = [k

(T), …, k

(nT)]

, nT is limited by the

available duration of y(t). The cardiac beat period T

can be obtained from T = argmax

∈

(

)

, where

and

are the singular values of S(γ) and the

search interval

is defined using physiological

limits of admissible heart rates. Once each heart

cycle section of the signal’s envelop has been

identified, time domain similarity is checked using

the inner product. Only those cycles which exhibit a

similarity towards its neighbor greater than 0.8 are

retained for further processing. The second test

performed during this phase is performed in the

time-frequency bands. First the spectrogram (0-

600Hz) is split into 15 contiguous, non-overlapping

frequency bands. Since the main energy sources in

HS are due to the S1 and S2 components, it is

observed that the envelops in each time-frequency

band tend to exhibit linear dependent auto-

correlation functions (with decreasing linear

dependency for natural and bioprosthetic valves and

with increasing linear dependency for mechanical

valves) with aligned peaks (see fig. 3). The linear

dependency is assessed using the SVD of the matrix

Λ, whose rows are the autocorrelation functions of

the time-frequency bands. Namely, it is observed

that it has to verify

≥

≤

, where

k+1

)

and

represents the kth singular value

Λ. The heart cycle with the highest average

similarity (radial distance) with respect to all

available heart cycle template candidates is selected

as the template.

Once the reference heart sound has been defined,

phase II is initiated where a template matching

approach is applied to each HS signal window using

the following spectral and temporal features: first the

A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS

153

correlation between spectral power of the template

and the signal under analysis is assessed. If it is

greater than 0.98, then the signal is subject to a

temporal energy test (required to capture very short

duration contaminations). In this test, the energy of

each 50ms signal window is checked against the

energy of the template. The complementary

contributions of these two features in the noise

contamination problem are shown in fig.4.

Figure 3: a) Heart sound from mechanical valve. b)

Spectrogram. c) Auto-correlation functions of the time-

frequency bands.

2.2 Segmentation

HS segmentation into its main constituent parts is

approached using two distinct methods: one is based

on the signal’s envelogram, the other is based on a

wavelet-simplicity filter. The former algorithm is

very efficient computationally. However, its

performance degrades rapidly for HS with murmur.

This type of HS are segmented using a method

developed by the team based on the wavelet-

simplicity filter, which is computationally more

demanding. To automatically select between both

methods, a selection stage has been incorporated into

the segmentation module (see fig. 5).

Heart sounds, particularly those with murmur,

contain nonlinear and non-Gaussian information that

is not tackled by the widely known Fourier or time-

frequency based analysis techniques. Nonlinear

Figure 4: (a) Noise contamination detection results. (b)

Spectral correlation feature. (c) Temporal energy feature.

Figure 5: HS segmentation method.

dynamic techniques not only enable to deal with the

nonlinearity and the non-Gaussianity of a signal, but

also project its dynamic behavior, such as chaos and

complexity, in the state space or the phase space that

is constructed using embedding theory. Based upon

the constructed phase space, the features of a heart

sound signal can be computed. In the proposed

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

154

method, the degree of chaos is measured via the

Lyapunov exponents estimation.

Suppose the heart is considered as a nonlinear

dynamical system X(t + 1) = F[X(t)] that generates

the heart sound time series x(t), t = 1....N . Signal x(t)

can be treated as a one dimensional projection of the

unknown multidimensional dynamic variable X(t).

Phase space transformation of the one dimensional

observation x(t) is performed using the embedding

theorem, attributed to Taken’s theorem, which states

that, using some suitable assumptions, a phase space

can be formed that is topologically equivalent to an

original system (Abarbanel, 1996). The method of

delay is applied to reconstruct the attractor in the

multidimensional space or embedding space P, i.e.

(t) = [x(t), x(t −

), ....., x(t − (m − 1) τ))]

∈

where i = 1, 2, 3...P and yi(t) are row vectors of the

embedding matrix Y(t). To determine the exponents

from the embedded matrix Y(t), the nearest neighbor

points are located to measure their distance from the

initial points as given in equation.

− t

log

()

k−1

()

k=1

∑

where M is the number of repetitions the trajectory

takes in traversing the entire data and denotes the

Lyapunov exponents. For a chaotic dynamical

system it is observed that the Lyapunov exponents

are positive (Abarbanel, 1996). Fig. 6 depicts the

average of 150 exponents obtained from 35 HS clips

(20 clips without murmur and 15 clips with murmur).

As can be observed, HS without murmur are

significantly less chaotic. The decision stage in fig. 5

is implemented using a simple threshold decision

rule.

The segmentation method based on the signal’s

envelop is basically formed by two simple steps

(Kumar et al., 2006a): (i) first the S1 and S2

candidates are identified using the zero-crossings of

the envelop of the approximation coefficients of the

level wavelet decomposition. The envelop is

computed with a running average of the Shannon

energy. The identification of the S1 and S2

components is based on the observation that pressure

gradients are higher across the aortic valve compared

to the mitral valve. Hence, the S2 heart sound should

exhibit more pronounced high frequency

components compared to S1 or S3. In order to

capture this, a new high frequency feature was

introduced. This new feature is composed by the

Shannon energy of the detail coefficients of the

wavelet transform. As can be seen in fig. 6 (top), this

signature coupled to some simple physiological

motivated rules enable the discrimination between

the different components of the heart sound.

Figure 6: (top) High frequency signature applied to detect

the S2 sounds; HFS and LFS stand for high and low

frequency segment, respectively.. (bottom) Lyapunov

exponents for sound heart sounds with and without

murmur.

Regarding the wavelet-simplicity filter algorithm, it

follows the same steps of the algorithm we

developed using the Wavelet-Simplicity transform

(Kumar et al., 2006). Therefore, only fundamental

changes in the steps of the basic algorithm are

described herein. Murmurs occur between S1 and S2

or S2 and S1 sounds. Therefore, the first task

consists of the identification of the boundaries of the

S1 and S2 sounds. The main steps for achieving S1,

S2 and murmur separation using the strength and

simplicity features are (see fig.7):

Step 1: Heart sound is decomposed using the

wavelet db6. The approximation coefficients are

used in further processing.

Step 2: Simplicity (S

) and global strength (GS

where l is the depth of wavelet decomposition, of the

decomposed signal is computed.

A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS

155

Figure 7: Wavelet-Simplicity Filter segmentation

algorithm.

Step 3: The S1 and S2 components of a heart sound

exhibit high strength and simplicity, hence clear

peaks can be seen in these curves (see fig. 8). In

severe heart murmurs, murmurs overlap S1 or S2

sounds. Other unknown sounds may occur due to

physiological events (e.g. S3) that exhibit similar

characteristics of S1 and S2 components. Usually,

S1 and S2 sounds exhibit relatively high simplicity

as well as strength, whereas other artifacts exhibit

high simplicity but on the contrary low strength.

Therefore, the width (or duration) of S1 and S2

sounds are separately segmented using both feature

curves. For this task, the peak peeling algorithm

(PPA) (Hadjileontiadis and Rekanos, 2003) based

upon an iterative thresholding process is applied.

PPA is applied first to the GS curve and then to the S

curve successively. Subsequently, start and stop

times of S1 and S2 sounds are achieved and can be

gated. The segmented time gates using both feature

curves are shown in fig. 8.

Step 4: It is observed from fig. 8 that correct start

and stop times of S1 and S2 sounds can be achieved

by common segmented time gates in both

thresholded feature curves.

Step 5: The suitable decomposition depth is found

by applying the mean square error criterion on gated

decomposed heart sound signal.

To segment occurrences of the S3 sound, two

additional steps are carried out using physiological

motivated criteria:

1 - Availability of S3 check: two criteria have been

considered to check for the availability of S3 sounds

in a heart sound sample: (i) if the duration of more

than 75% of S2 sounds exceed 250ms. This occurs

when the segmentation algorithm was not able to

separate the S2 and S3 boundaries. (ii) If more than

75% small low complexity segments exhibiting low

duration (50ms-70ms) are detected in the diastolic

phase.

2 – Recognition of S3: S3 are characterized by low

loudness, small duration, low frequency range

(typically between 25-70Hz) and their diastolic

nature, i.e. S3 tend to originate around 150ms after

the onset of the A2 (aortic component of the S2).

Using these properties the following validation

criteria are considered:

Loudness: (loudness)

<1/3(loudness)

{S1,S2}

Simplicity: due to their lower spectral

content, S3’s simplicity tends to be higher

compared to simplicity of S1 and S2, i.e.

{S1,S2}

The time interval between the onset of S3

and the onset of the preceding S2 is

between 120-180ms.

The duration of S3 is between 40-70ms).

Figure 8: Segmentation results in severe (grade V) mitral

regurgitation murmur.

2.3 Murmur Characterization

This module of the toolbox performs murmur

classification using features extracted from the

systolic, i.e. S1-S2, or the diastolic intervals, i.e. S2-

S1. The approach followed is a classical pattern

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

156

recognition approach composed by two layers:

feature extraction and classifier (a SVM with cubic

polynomial kernel function, trained using the one-

against-one binary classification). The classifier

considers seven distinct classes of mrmur: 1) Aortic

Regurgitation (AR), 2) Aortic Stenosis (AS), 3)

Mitral Regurgitation (MR), 4) Pulmonary

Regurgitation (PR), 5) Pulmonary Stenosis (PS), 6)

Subaortic Stenosis+Ventricular Septal Defect

(SAS+VSD), 7) Systolic Ejection (SE). It should be

noted that murmur presence detection is based on

Lyapunov exponents described earlier.

Murmur classification is a challenging task, whose

success is mainly conditioned by the quality of the

features. The features implemented in this toolbox

have been obtained using a feature selection

approach from a pool of 256 features. These features

have been collected using a two-fold approach:

features have been collected from two well-known

methods described in literature and a set of new

features has been introduced (Kumar et al., 2010).

Regarding the feature sets taken from the literature,

the sets introduced by Alhstrom et al. (2006) and by

Olmez and Dokur (2003) have been considered. The

most discriminative features have been selected

using Pudil’s sequential floating point forward

selection method. The module allows for two

alternative sets of features: the first set is composed

by 17 features that have been selected from the

aforementioned 256 feature pool, and the second one

is composed by 10 features selected among a much

smaller pool of features defined by the team. By

default we favor the less complex solution, although

(as will be discussed later) it exhibits a slightly

smaller sensitivity and specificity compared to the

first set. The implemented features in the second

feature set are those listed in table 1. The transition

rate is defined by transition rate = T

asc

desc

, where

Tasc is the transition time taken from the first

minimum of the energy curve to the maximum

energy, and T

dsc

is the time interval from the energy

maximum to the last subsequent minimum energy.

The remaining features are well-known in signal

processing.

Table 1: feature set for murmur classification.

Loudness

Transition Ratio

Fundamental frequency

Spectral power (100-200Hz)

Spectral power (200-300Hz)

Zero crossing rate

Skewness (time domain)

Spectral Shape

Spectral Flux

Max. Lyapunov Exponent

2.4 Cardiac Function Assessment

The assessment of the left ventricle cardiac function

is based on the extraction of the left ventricle systolic

time intervals (STI), i.e. the pre-ejection period

(PEP) and the left ventricule ejection time (LVET).

These are of major diagnostic importance, since it is

this ventricle’s function to insure the blood flow in

the systemic circulation. STI are defined by the

events of the aortic valve. Namely, PEP is defined by

the time interval between R-peak of the ECG and the

opening of the aortic valve, while LVET corresponds

to time span between the closing and the opening

events of this valve. We have shown (Carvalho et

al., 2009) that S1 and S2 can be applied to extract

the aortic valve events from S1 and S2 using

synchronized echocardiography and HS under

resting conditions. It should be mentioned that, the

framework has other methods to extract STI that can

be applied. For instance, when no ECG is available,

the PPG and the HS can be combined to extract the

STI. These might also be estimated using the ICG

signal, if available. A comparative analysis of some

of these methods and principles in STI estimation

can be found in (Carvalho et al., 2010).

The details regarding the algorithm for the detection

of the aortic events using HS were presented in

(Paiva et al., 2009). The method is based on a

Bayesian approach using instantaneous amplitude.

Once the beat-by-beat STI have been extracted, the

toolbox enables the calculation of the following

cardiac function measures:

Corrected STI with Respect to Heart Rate and

Classification:

The implemented correction

algorithms are those described in (Weissler et al.,

1968) and (Warrington et al., 1988). For STI

correction under exercise, the correction steps

described by Mertens et al. (1981) have been

considered in the toolbox. The toolbox presents

diagnosis information regarding if the STI are

pathological or not.

Contractility Index and Classification: The

contractility index PEP/LVET is computed average

runs of 5 beats. Heart Failure diagnosis is

automatically provided based on clinically validated

threshold.

Stroke Volume and Cardiac Output: The beat-to-

beat as well as the average stroke volume and the

cardiac output are calculated using the model

described in (Rietzschel et al., 2001). It should be

mentioned that these parameters are also extracted in

the ICG toolbox of the framework, where the

Bernstein and Kubicek models have been

A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS

157

implemented (see e.g. Wang et al., 1995).

2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8

100

150

200

250

t(s)

Echocardiography

2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8

-0.5

0.5

t(s)

Electrocardiograms

2.8 2.9 3 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8

-0.5

0.5

t(s)

Phonocardiogram

RPEAKS

AVO from ECHO

AVC from ECHO

AVO from PCG

AVC from PCG

Figure 9: Synchronized echocardiography and heart

sound.

2.5 S2 Split Detection

Pulmonary hypertension (PH) is a serious heart

condition that is difficult to diagnose. Heart sounds

is one of the most relevant diagnosis signal. Usually,

PH leads to wide S2 split between the aortic

component (A2) and the pulmonary component (P2).

Loud P2 is another usual consequence of PH. The

toolbox implements a simple algorithm to assess S2

splitting. The following steps compose the method:

Step 1: S2 frequency range is typically limited to

240Hz. The first step is low-pass filtering using a

Butterworth filter with 240Hz cut-off frequency.

Step 2: The signal’s envelop is extracted using the

Hilbert transform.

Step 3: The two most prominent are extracted. If

their amplitude ratio is greater than a predefined

threshold, then a split is assumed.

Step 4: The split duration is estimated as the time

interval between the two peaks of the signal’s

envelop (see fig. 10).

Figure 10: S2 Split. Upper curve represents the signal’s

envelop. The lower dashed curve is the S2 heart sound.

Time split interval as well as A2 and P2 components are

shown.

3 RESULTS AND DISCUSSION

Table 2 presents the sensitivity and specificity results

of the algorithms implemented in the heart sound

toolbox of the framework. The STI estimation

entries, i.e. PEP, LVET and RS2 entries, refer to the

absolute estimation error with respect to

echocardiography (the clinical gold standard). These

results were obtained using heart sounds acquired at

several hospitals from typical target populations, i.e.

patients suffering from several types of cardio-

vascular diseases such as atrial fibrillation,

tachycardia, premature ventricular contractions,

several types of valve problems with regurgitation

and stenosis, patients with artificial valve implants,

as well as several degrees of heart failure. One

exception to this is the data acquisition protocol

followed to assess the STI measurement algorithms.

In this case, only healthy subjects have been used so

far. The data acquisition study with patients suffering

from heart failure is currently being carried out. It

should also be mentioned that the data collection

study with CVD patients for S2 split assessment is

also ongoing. Regarding the data acquisition for

noise detection, the protocol followed included

contaminations by several distinct internal and

external noise sources at different intensity levels.

All databases have been collected and annotated

under medical supervision. Table 3 summarizes the

population characteristics and the amount of data

collected for each validation database.

Table 2: Summary of results.

Function SE/Abs. Error SP/Corr.

Noise detection 95.88% 97.56%

Segmentation

(without murmur)

97.95% 98.20%

Segmentation

(grade I-IV murmur)

91.09% 95.25%

S2 Split* - -

S3 Identification 90.35% 92.35%

Murmur classification

(set of 10 features)

95.74% 95.01%

Murmur classification

(set of 17 features)

96.15% 96.16%

PEP

7.57±6.17ms

0.52

LVET

11.21±9.27ms

0.88

RS2

9.88±8.65ms

0.92

As can be observed from the results in table 2 and 3,

most of the algorithms developed by team and

integrated into the toolbox have been evaluated

thoroughly. Furthermore, these methods exhibit very

high sensitivity and specificity values. Regarding the

results achieved for STI, the achieved results so far,

suggest that HS enables much better results

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

158

compared to other competing measurement

principles for portable and non-invasive devices (a

detailed analysis can be found in (Carvalho et al.,

2010)). As already mentioned, these results have still

to be confirmed for CVD patients. Regarding the

evaluation of the S3 identification module, it should

be mentioned that currently the algorithm has been

evaluated on sound clips collected from 5 patients.

Hence, the provided results should be considered as

preliminary. As for the S2 split algorithm, evaluation

as been performed only on healthy subjects so far.

Table 3: Validation conditions.

Function N BMI Age

Noise detection 71

25.1±7.8kg/m

35.3±12.0y

Segmentation

(without mur.)

24.4±1.5kg/m

32.6±9.7y

Segmentation

(grade I-IV mur.)

24.9±2.3kg/m

54.73±6.0y

Murmur classif. 51

25.4±2.2kg/m

64.65±8.6y

S2 Split* - - -

S3 Identification 5 NA

15.7±8.7y

STI 33

24.5±2.4kg/m

29.7±8.5y

Given the achieved maturity level of the toolbox, it

is being used to deploy clinical applications.

Currently, the team is developing three distinct

applications using the framework: the first

application is called the intelligent stethoscope that

enables the automatic annotation of HS to support

the decision of the physician (for details, the reader

may refer to (Ramos et al., 2011)); the second

application build on top of the first one and is

intended to auscultation training; finally the third and

last application targets prosthetic heart valve implant

dysfunction detection. Applications related to heart

failure management are planned, once the STI

measurement module tests have been concluded.

4 CONCLUSIONS AND FUTURE

WORK

Heart sound is a valuable biosignal to build

diagnosis systems for cardiovascular diseases for the

daily acute clinical practice as well as for systems

dedicated to long-term follow-up of chronic CVD

patients. In this paper we introduce a Matlab toolbox

for acoustic cardiac signal processing. This toolbox

is integrated into a framework for cardiac signal

processing that includes a general real-time signal

acquisition toolbox to interface medical sensor

networks and a collection of signal analysis

toolboxes for the most pertinent signals to deploy

portable and non-invasive devices for CVD

diagnosis. The main algorithms developed

specifically for the heart sound toolbox are outlined.

These include solutions for the main challenges that

are encountered in real life applications based on

heart sounds. In comparison to other existing heart

sound processing frameworks, the proposed toolbox

includes methods for the processing functionalities

that are commonly handled, i.e. noise contamination

detection, heart sound segmentation (including S3

identification) and murmur classification, but also

tackles problems that most known frameworks do

not contemplate. More specifically, methods to

detect S2 splitting and cardiac function assessment

are part of the proposed toolbox. To the best of the

authors’ knowledge, the proposed toolbox is the first

one that enables STI measurement using heart

sounds. This opens new application areas to heart

sounds such as heart failure management.

The proposed framework exhibits a significant

maturity level. Most of the integrated algorithms

have been tested using heart sound clips obtained

under medical supervision and using typical CVD

populations under real-life conditions. The achieved

results are comparable and in most cases exceed the

state of the art in competing methods. It should be

mentioned that the proposed algorithms for STI

measurement and S3 identification have still to be

fully evaluated using a significant database of data

collected from real CVD patients. This is an ongoing

task that will be finished in the near future. It is also

foreseen to continue the research of a more evolved

version of the S2 split detection module. More

specifically, currently the team is researching a

solution to accurately identify the onset of both S2

components, i.e. A2 and P2. This might enable to

correlate the time split to pulmonary artery pressure

measurement as was previously suggested by (Popov

et al., 2004).

ACKNOWLEDGEMENTS

This work was supported in part by SoundForLife

(PTDC/EIA/68620/2006; FCOMP-01-0124-

FEDER-007243) financed by the Portuguese

Foundation for Science and Technology.

REFERENCES

Abarbanel H., 1996, Analysis of observed chaotic data,

Springer- Verlag New York, Inc., 87–90.

A FRAMEWORK FOR ACOUSTIC CARDIAC SIGNAL ANALYSIS

159

Abbas A, Bassam R, 2009, Phonocardiography signal

processing, synthesis lectures on biomedical

Engineering, Morgan and Claypool Publishers.

Ahlstrom C., Hult P., Rask P., Karlsson J., Nylander E.,

Dahlstro U., Ask P., 2003, Feature extraction for

systolic heart murmur classification. Annals of

Biomed. Engg., 34(11):1666–1677.

Allender S., Scarborough P., Petov P., Rayner M., Leal J.,

Luengo-Fernandez R., Gray A., 2008, European

Cardiovascular Disease Statistics 2008, European

Heart Network.

Carvalho P., Paiva R., Couceiro R., Henriques J., Quintal

I., Muehlsteff J., Aubert X., Antunes M., 2009,

Assessing Systolic Time-Intervals from Heart Sound: a

Feasibility Study, IEEE-EMBS.

Carvalho P., Paiva R., Henriques J., Antunes M., Quintal

I., Muehlsteff J., 2011, Robust Characteristic Points

for ICG: Definition and Comparative Analysis,

Biostec: Biosignals. (submitted)

Carvalho P., Paiva R., Henriques J., Quintal I., Muehlsteff

J., Aubert X., Antunes M., 2010, Comparison of

Systolic Time Interval Measurement Modalities for

Portable Devices, IEEE-EMBS.

Chan G., Middleton P., Celler B., Wang L., Lovell N.,

2007, Automatic detection of left ventricular ejection

time from a finger photoplethysmographic pulse

oximetry waveform: comparison with Doppler aortic

measurement, Physiol. Meas. 28:439–452

Durand L. G. and Pibarot P., 1995 Digital signal

processing of the phonocardiogram: review of the

most recent advancements, Crit. Rev. Biomedical

Engineering, 23:163–219

Habetha J., 2006, The MyHeart Project – Fighting

Cardiovascular Diseases by Prevention and Early

Diagnosis, IEEE-EMBS.

Hadjileontiadis L., Rekanos I., 2003, Detection of

explosive lung bowel sounds by means of fractal

dimension, IEEE Signal Proc. Letters, 10(10):311-

314.

Henriques J., Carvalho P., Harris M., Antunes M.,

Couceiro R., Brito M., Schmidt R., 2008, Assessment

of Arrhythmias for Heart Failure Management,

phealth2008 – Int. Workshop on Wearable Micro and

Nanosystems for Personalised Health.

Javed F., Venkatachalam P., Fadzil A., 2006, A Signal

Processing Module for the Analysis of Heart Sounds

and Heart Murmurs, Journal of Physics: Conference

Series; International MEMS Conference, 34:1098–

1105.

Kumar D., Carvalho P., Antunes M., Henriques, J.,

Eugénio L., Schmidt R., Habetha, J., 2006a, Detection

of S1 and S2 Heart Sounds by High Frequency

Signatures, IEEE-EMBS.

Kumar D., Carvalho P., Antunes M., Henriques, J.,

Eugénio L., Schmidt R., Habetha, J., 2006, Wavelet

Transform and Simplicity based Heart Murmur

Segmentation, Computers in Cardiology, 33:173-176.

Kumar D., Carvalho P., Couceiro R., Antunes M., Paiva

R., Henriques J., 2010, Heart Murmur Classification

using Complexity Signatures, Int. Conf on Pattern

Recognition.

Lam M., Lee T., Boey P., Ng W., Hey H., Ho K., Cheong

P., 2005, Factors influencing cardiac auscultation

proficiency in physician trainees, Singapore Med J;

46(1):11.

Mertens H., Mannbach H., Trieb M., Gleichmann U.,

1981, Influence of Heart Rate on Systolic Time

Intervals: Effects of Atrial Pacing versus Dynamic

Exercise, Clin. Cardiol., 4: 22-27.

Oh J., Tajik J., 2003, The return of cardiac time intervals.

The Phonix is rising., J. of the Am. Col. of Cardiology,

42(8):1471-1474.

Olmez T., Dokur Z., 2003, Classification of heart sounds

using ans artifical neural network, Pattern Recognition

Letters, 617-629.

Paiva P., Carvalho P., Aubert X., Muehlsteff J., Henriques

J., Antunes M., 2009, Assessing PEP and LVET from

Heart Sounds: Algorithms and Evaluation, IEEE-

EMBS.

Pease A., 2001, If the heart could speak, Pictures of the

Future, 60–61.

Popov B. Sierra G. Durand L. Xu J., Pibarot P., Agarwal

R., Lanzo V., 2004, Automated extraction of aortic

and pulmonary components of the second heart sound

for the estimation of pulmonary artery pressure, IEEE-

EMBS.

Rajan S., Doraiswami R., Stevenson M., Watrous R.,

1998, Wavelet based bank of correlators approach for

phonocardiogram signal classification, IEEE-SP Int.

Symposium on Time-Frequency and Time-Scale

Analysis , 77 – 80.

Ramos J., P. Carvalho, R. Paiva, L. Vale, J. Henriques,

2011, Intelligent Phonocardiogram Analysis And

Representation Tool, Biostec: HealthInf. (submitted)

Rietzschel E., Boeykens E., Buyzere M. Duprez D.

Clement D., 2001, A comparision between systolic

and diastolic pulse contour analysis in the evaluation

of arterial stiffness, Hypertension, 37:e15-e22.

Syed Z., Leeds D., Curtis D., Nesta F., Levine R., Guttag

J., 2007, A Framework for the Analysis of Acoustical

Cardiac Signals, IEEE Trans. On Biomedical Eng.,

54(4): 651-662.

Tavel M. E., 1967 Clinical Phonocardiography and

External Pulse Recording (Year Book Medical

Publishers, Inc.)

Wang X,, Sun H,, Water J,, 1995, An advanced signal

processing technique for impedance cardiography,

IEEE Trans. On BioMed. Eng., 42(2) 224-30.

Warrington S., Weerasuriya K., Burgess C., 1988,

Correction of systolic time intervals for heart rate: A

comparison of individual with population derived

regression equations, Br. J. Clin. Pharmacol.,

26(2):155-165.

Weissler A., Harris W., Schoenfeld C., 1968, Systolic

Time Intervals in Heart Failure in Man, Circulation,

37; 149-159.

WHO 2005, Preventing Chronic Disease: a Vital

Investment, World Health Organization.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

160