
OPTIMIZATION OF A SOLID STATE FERMENTATION
BASED ON RADIAL BASIS FUNCTION NEURAL NETWORK
AND PARTICLE SWARM OPTIMIZATION ALGORITHM
Badia Dandach-Bouaoudat, Farouk Yalaoui, Lionel Amodeo
University of Technology of Troyes, 12 rue Marie Curie, Troyes, France
Franc¸oise Entzmann
Ets J.Soufflet, Quai Sarrail, Nogent sur Seine, France
Keywords:
Solid state fermentation, Enzyme production, Optimization, Response surface methodology, Neural network,
Particles swarm optimization algorithm.
Abstract:
Radial basis function neural network (RBF) and particle swarm optimization (PSO) are used to model and
optimize a solid state fermentation (SSF) for production of the enzyme. Experimental data reported in the lit-
erature are used to investigate this approach. The response surface methodology (RSM) is applied to optimize
PSO parameters. Using this procedure, two artificial intelligence techniques (RBF-PSO) have been effec-
tively integrated to create a powerful tool for bioprocess modelling and optimization. This paper describes the
applications of this approach for the first time in the solid state fermentation optimization.
1 INTRODUCTION
Fermentation processes are used to produce various
substances in the pharmaceutical, chemical and food
industries. The performance of fermentation pro-
cesses depends on many factors, including pH, tem-
perature, ionic strength, agitation speed, and aera-
tion rate in the aerobic fermentation (Kennedy and
Krouse, 1999). To achieve the best performance
of fermentation processes, various process optimiza-
tion strategies were developed by scientists. The
most frequently used optimization is response sur-
face methodology (RSM), which includes factorial
design and regression analysis, seeks to identify and
optimize significant factors to maximize the response
(cell density, high yields of the desired metabolic
products or enzyme levels in the microbial system).
RSM yields a model, which describes the relationship
between the independent and dependent variables of
the processes. The most widely used simulating mod-
els are second order polynomials (Ceylan et al., 2008)
and (Chang et al., 2008), and now RSM has been
widely applied in the bioprocess optimization (Ku-
namneni and Singh, 2005) and (Ustok et al., 2007).
In recent years, a limited number of studies have
investigated the possibility of using non-statistical
techniques, such as artificial intelligence (AI), for de-
veloping non-linear empirical models. The most com-
monly used AI are artificial neural networks (ANNs).
ANNs are superior and more accurate modelling tech-
niques when compared to RSM and represent the non-
linearities in a much better way (Dutta et al., 2004).
The most frequently used ANNs is a radial basis func-
tion (RBF) neural network. As a universal function
approximator under certain general conditions (Wil-
son et al., 1999).
One type of evolutionary technique used in com-
puter science is particle swarm optimization (PSO).
This technique allows one approximate optimization
and search problem solutions. Kennedy and Eberhart
were the first to propose the PSO algorithm (Kennedy
et al., 1995). This algorithm is based on the premise
that evolution of a species is advanced by the so-
cial sharing of information among members of the
said species. PSO is a perfect candidate of optimiza-
tion tasks based on a number of advatages compared
to other algorithms. The PSO algorithm is strong
enough to handle complex situations such as non-
linear and non-convex design spaces with discontinu-
ities. Also continuous, discrete and integer variable
287
Dandach-Bouaoudat B., Yalaoui F., Amodeo L. and Entzmann F..
OPTIMIZATION OF A SOLID STATE FERMENTATION BASED ON RADIAL BASIS FUNCTION NEURAL NETWORK AND PARTICLE SWARM
OPTIMIZATION ALGORITHM.
DOI: 10.5220/0003136202870292
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 287-292
ISBN: 978-989-8425-36-2
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

types can be handled easily. Also, the PSO optimiza-
tion method is more efficient than other equally robust
designs. There are fewer function evaluations yet the
results are of equal or better quality than competitors
(Hu et al., 2003) and (Hassan et al., 2005).
In this work, RBF neural network coupling PSO
algorithm (RBF-PSO) was used to model and opti-
mize the mixing performance of solid state fermenta-
tion. Three independent process variables including
temperature, agitation, and inoculums size were con-
sidered for optimization. The optimization objective
was to achieve the maximum alpha-amylase activity
at an optimal combination of three independent vari-
ables. The RBF neural network was used to develop
the mathematical function of alpha-amylase activity
with temperature, agitation, and inoculums size. Then
PSO algorithm was used to execute the optimization
task to achieve the maximum alpha-amylase activity.
The response surface methodology (RSM) is applied
to optimize PSO parameters.
2 MODELIZATION
2.1 RBF Neural Network
RBF neural network is structured by embedding ra-
dial basis function with a two-layer feed-forward neu-
ral network. Such a network is characterized by a set
of input and set of outputs. In between the inputs and
outputs there is a layer of processing units called hid-
den units. Each of them implements a radial basis
function. The architecture of RBF network is shown
in Figure 1.
Figure 1: structure of RBF neural network for process mod-
eling.
Mathematically RBF neural network can be for-
mulated as:
g(x) =
m
∑
k=1
λ
k
ϕ
k
(kx
i
− c
k
k) (1)
Where m is the neuron number of hidden layer, which
is equal to cluster number of training set. kx
i
− c
k
k
represents the distance between the data point x
i
and
the RBF center c
k
.λ
k
is the weight related with RBF
center c
k
. Therefore, the output of RBF neural net-
work is a weighted sum of the hidden layer’s activa-
tion functions. Various functions have been tested as
activation functions for RBF networks. Here we adopt
the most commonly used Gaussian RB functions as
basis functions shown in equation (2):
ϕ
k
(x
i
) =
R
k
(x
i
)
∑
m
i=1
R
i
(x
i
)
(2)
R
k
(x
i
) = exp(−
kx
i
− c
k
k
2
2σ
2
k
) (3)
In equation (3), σ
k
indicates the width of the kth
Guassian RB functions. One of the σ
k
selection meth-
ods is shown as follows.
σ
2
k
=
1
M
k
∑
x∈θ
k
kx
i
− c
k
k
2
(4)
here θ
k
the kth cluster of training set, and M
k
is
the number of sample data in the kth cluster.
3 OPTIMIZATION
3.1 PSO Algorithm
Stochastic in nature, the particle swarm process up-
dates the position of each particle in the swarm using
the velocity vector. This vector is updated using the
memory of each particle and the entire swarm. This
allows the position of each individual particle to be
updated based on the entire swarm. As the swarm
adapts to its environment each particle can return to
regions of space that are promising and also search
for better positions.
Numerically, the position x of a particle i at iter-
ation k + 1 is updated as shown in equation (5) and
illustrated in figure 2.
x
i
k+1
= x
i
k
+ v
i
k+1
(5)
Where v
i
k+1
is the corresponding updated velocity
vector, the velocity vector of each particles is calcu-
lated as shown in equation (6),
v
i
k+1
= wv
i
k
+ w
1
r
1
(p
i
k
− x
i
k
) + w
2
r
2
(p
g
k
− x
i
k
(6)
Where v
i
k
is the velocity vector at iteration k, r
1
and r
2
represents random numbers between 0 and 1;
p
i
k
represents the best ever particle position of particle
i, and p
g
k
corresponds to the global best position in the
swarm up to iteration k.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
288
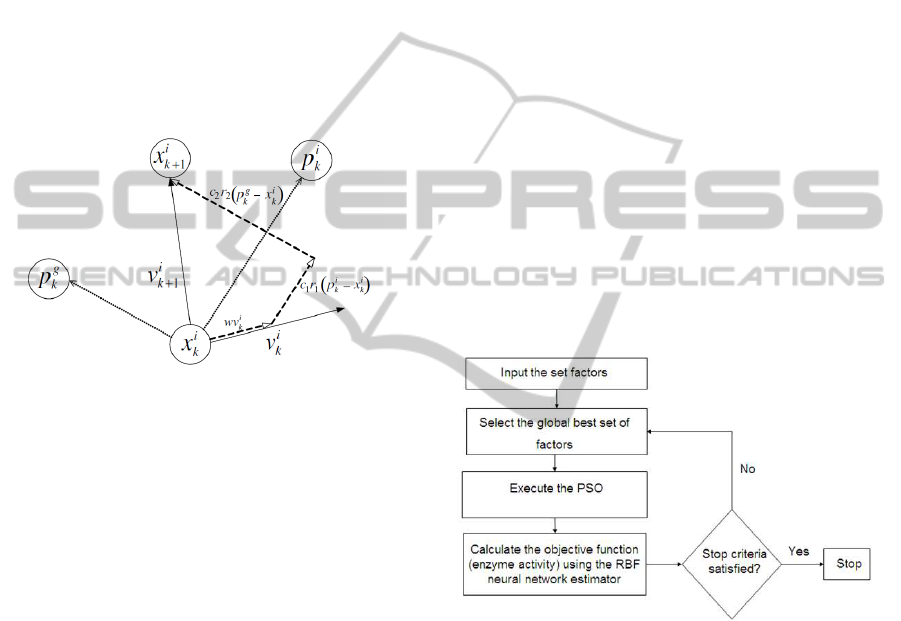
Terms that remain are parameters that depend on
the problem. These include w
1
, w
2
and w, which stand
for the particles confidence in itself (cognitive param-
eter) and in the swarm (social parameter) and also
inertial weight, respectively. The PSO convergence
behavior, which is used to control the exploration ca-
pabilities of the swarm, relies largely on the inertial
weight of the particle. The inertial weight impacts the
current velocity, which is based on previous veloci-
ties. Therefore, as the inertial weight changes, so does
the ability of the particle to roam. If inertial weight is
large, the particle can explore the design space in a
broader manner, while small inertial weights limit the
updates of velocity to local regions within the design
space.
Figure 2: PSO position and velocity update.
3.2 Response Surface Methodology
(RSM)
Response surface methodology combines statistical
experimental designs and empirical model building
by regression for the purpose of process or prod-
uct optimization. Statistical experimental design is
a powerful method for accumulating informations
about a process efficiently and rapidly from a small
number of experiments, there by minimizing exper-
imental costs. An empirical model is then used to
relate the response of the process to some indepen-
dent variables. This usually entails fitting a quadratic
polynomial to the available data by regression anal-
ysis. The general from of the quadratic polynomial
is:
Y = b
0
+
∑
b
i
X
i
+
∑
b
i
X
2
i
+
∑
b
ij
X
i
X
j
+ e (7)
WhereY is the predicted response, X
i
and X
j
stand
for the independent variables, b
0
is the intercept, b
i
and b
i, j
terms are regression coefficients, and e is a
random error component. A near-optimum solution
can then be deduced by calculating the derivatives of
equation (7) or by mapping the response of the model
into a surface contour plot.
4 RESULTS AND DISCUSSION
4.1 RBF Modeling
In the RBF estimator for the fermentationexample ex-
amined in this work, there are three nodes (x
1
: tem-
perature (
◦
C), x
2
: agitation (rpm) and x
3
: Log
10
of
inoculums size (spore/ml) in the input layer and an
output node for alpha-amylase activity (Y). with the
given structure, the RBF neural network is trained by
the sampling data imported from (Kammoun et al.,
2008) to obtain a desired estimator.
Here the R
2
of 99.8% indicates that the experi-
mental and predicted values are in a good agreement.
4.2 Optimization by PSO Algorithm
In the present work, we used the RBF neural net-
work to produce the fitness function. We developed
a (RBF-PSO) algorithm with Matlab software, this
algorithm has 2 steps: modeling and optimization,
various steps involved in this study were represented
schematically in Figure 3.
Figure 3: Schematic representation of RBF-PSO algorithm
for bioprocess optimization.
Based on the particle and velocity updates as ex-
plained in equation (6), the PSO algorithm is con-
structed as follows:
1. Initialize a set of particles positions x
i
0
and veloci-
ties v
i
0
randomly distributed throughout the design
space bounded by specified limits, and set p
i
k
=x
i
k
.
2. Evaluate the objective function values f(x
i
k
using
the design space positions x
i
k
. That is, employ the
particle’s position vector as the the input of RBF
estimator.
3. Update the optimum particle position p
i
k
at current
iteration (k) and global optimum particle position
p
g
k
.
OPTIMIZATION OF A SOLID STATE FERMENTATION BASED ON RADIAL BASIS FUNCTION NEURAL
NETWORK AND PARTICLE SWARM OPTIMIZATION ALGORITHM
289

4. Update the position of each particle using its pre-
vious position and update velocity vector as spec-
ified in equation (5) and equation (6).
5. Repeat steps 2-4 until the stopping criteria is met.
For the current implementation the stopping cri-
teria is defined based on the number of iterations
reached.
4.3 Tuning PSO Parameters
The role of the inertia weight w, plays a critical role in
the PSO’s convergence behavior in equation (6). The
inertia weight should consist of a trade-off between
global and local exploration abilities of the swarm
to therefore control the impact of previous veloci-
ties on the current velocity. Large inertia weight re-
sults in particles searching new areas, while a small
inertia weight results in particles exploring locally.
By finding a suitable value of inertia weight, a bal-
ance between wide-range and local exploration can
be acheived. By doing this, the optimum solution can
be found the most efficiently and with the fewest itera-
tions. Through experimentation, it was found that set-
ting the inertia weight to a high level results in global
exploration, which in turn produces more results (Shi
and Eberhart, 1998). This value can then be lowered,
refining the solutions. Therefore, a value of w start-
ing at 1.2 and gradually declining towards 0 can be
considered as a good choice for w.
The algorithm can be further improved by fine-
tuning the parameters w
1
and w
2
, in equation (6).
the results could be converged on faster and the lo-
cal explorat alleviated. In (Kennedy, 1998) an ex-
tensive study of the acceleration parameter in PSO’s
first version can be found. Recent work has also come
up with further suggestions for choosing w
1
and w
2
.
This work suggests that it may be in one’s best inter-
est to choose w
1
, the cognitive parameter, to be larger
than w
2
, the social parameter, with the limitation that
w
1
+ w
2
≤ 4 (Carlisle and Dozier, 2001).
The parameters r
1
and r
2
are used to maintain the
diversity of the population, and they are uniformly
distributed in the range [0, 1].
In this work, optimization of the parameters of the
PSO algorithm:
• N: swarm size ,
• w
1
: cognitive parameter,
• w
2
: social parameter,
was done by Box-Behnken design especially
made to require three levels coded as (-), (0) and
(+) (N = 13) (13 experiments and three factors at
three levels) under the response surface methodology
(RSM). Table 1 shows the different levels of each of
the parameters.
Table 1: Parameters values for Box-Behnken design.
Factors Basical Variation Value
level interval of the factor
w
1
: 2 2 0
Cognitive 2
parameter 4
w
2
: 2 2 0
Swarm 2
parameter 4
N: 65 35 30
Swarm 65
size 100
Table 2: Box-Behnken experimental design used to opti-
mize parameters of PSO algorithm.
PSO code w
1
w
2
N Alpha-amylase
activity (U/ml)
PSO 1 0 2 30 40.3668
PSO 2 0 2 100 40.3478
PSO 3 4 2 30 39.0155
PSO 4 4 2 100 40.3694
PSO 5 2 0 30 24.0529
PSO 6 2 0 100 29.7599
PSO 7 2 4 30 39.2980
PSO 8 2 4 100 40.0989
PSO 9 0 0 65 27.9151
PSO 10 4 0 65 27.4070
PSO 11 0 4 65 40.3685
PSO 12 4 4 65 35.0228
PSO 13 2 2 65 40.3731
Box-Behnken design is a fractional factorial de-
sign obtained by combining two-level factorial de-
signs with incomplete block designs. The response
surface methodology was used to analyses the exper-
imental design data. In order to be correlated to the
independent variables, the response variable was fit-
ted by a second order model.
Table 2 illustrates the Box-Behnken experimental
design of the three independent variables together
with the experimental result. By applying multiple
regression analysis on the experimental data, the
following second-order polynomial equation was
developed to clarify the relationship of the optimal
solution (Y), swarm size (N), cognitive parameter
(w
1
) and social parameter (w
2
):
Y = 40.374+ 0.980N− 0.898w
1
+ 5.707w
2
+
0.137N
2
− 0.487w
2
1
− 7.209w
2
2
+
0.343Nw
1
− 1.227Nw
2
− 1.209w
1
w
2
(8)
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
290

The R
2
of 98% indicates that the experimental and
predicted values are in a good agreement.
The response surface curves described by regres-
sion model are shown in figure 4.
Figure 4: Responses surface plot of cognitive parameter
(w
1
), social parameter (w
2
) and their mutual interaction on
alpha-amylase activity (Y), with an optimum level of swarm
size (N) of 65.
For equation derived from the differentiation of
equation (8), the optimal values of N, w
1
and w
2
in
coded units were found to be 0, -0.980 and 0.509 re-
spectively. Correspondingly, we can obtain the op-
timal combination of three parameters 65, 0.04 and
3.02 respectively.
In order to determine the maximum number of
generations, we have plotted the response curve in
function of number iteration, and we have presented
the results in figure 5. From figure, we deduce that
the maximum number of generations to reach the bet-
ter solution (Y = 40.3739U/ml) is 18 generations.
0 5 10 15 20
1.39
1.4
1.41
1.42
1.43
1.44
1.45
No. of iterations
Normalized alpha−amylase activity (U/ml)
Figure 5: Convergence process of solving optimization task
with PSO algorithm.
Table 3: Results after tuning parameters of PSO algorithm.
w: inertia parameter starting at 1.2 and
gradually declining
towards 0
N: Swarm size 65
w
1
:cognitive parameter 0.04
w
2
: Social parameter 3.02
G: Number of generation 18
4.4 Optimization Bioprocess Example
The result obtained are shown in the first row of table
4. As it is shown in the last column of the table, the
maximum value for alpha-amylase activity by RBF-
PSO algorithm is 40.3739U/ml which is much better
than the valueobtained by SM-GA algorithm reported
in (Dandach-Bouaoudat et al., 2010).
Table 4: Results after tuning parameters of PSO algorithm.
Approaches x
1
x
2
x
3
Y
(
◦
C) rpm spore/ml U/ml
RBF-PSO 21.88 303.22 7 40.3739
SM-GA 25.14 249.36 7.23 31.7
5 CONCLUSIONS
This work found that RBF neural network provided
good fits to experimental data. The hybrid RBF-PSO
approach described in this work serves as a viable al-
ternative for the modelling and optimization of fer-
mentation process. Alpha-amylase activity rises up to
40.37U/ml under the optimal culture conditions ob-
tained by RBF-PSO approach. This work indicates
that the coupling of RBF neural networks with PSO
algorithm has good predictability and accuracy in op-
timizing the multi-factor, non-linear, and time-variant
bioprocess. The knowledge and information obtained
here may be also helpful to the other industrial bio-
process to improve productivity.
Perspectives on work is conducting more expere-
ments, espacially for those data that have more pa-
rameters need to be optimized. We will also test
other artificial intelligence techniques for modelling
and optimization bioprocess and compared with the
proposed method.
OPTIMIZATION OF A SOLID STATE FERMENTATION BASED ON RADIAL BASIS FUNCTION NEURAL
NETWORK AND PARTICLE SWARM OPTIMIZATION ALGORITHM
291

REFERENCES
Carlisle, A. and Dozier, G. (2001). An off-the-shelf PSO.
In Proceedings of the workshop on particle swarm op-
timization. Indianapolis, IN: Purdue School of Engi-
neering and Technology, IUPUI.
Ceylan, H., Kubilay, S., Aktas, N., and Sahiner, N. (2008).
An approach for prediction of optimum reaction con-
ditions for laccase-catalyzed bio-transformation of 1-
naphthol by response surface methodology (RSM).
Bioresource technology.
Chang, S., Shaw, J., Yang, K., Chang, S., and Shieh, C.
(2008). Studies of optimum conditions for cova-
lent immobilization of Candida rugosa lipase on poly
([gamma]-glutamic acid) by RSM. Bioresource tech-
nology.
Dandach-Bouaoudat, B., Yalaoui, F., Amodeo, L., and
Entzmann, F. (2010). Optimization of a solid state
fermentation using Genetic Algorithm. In 5th Interna-
tional Symposium on Hydrocarbons and Chemistry-
Sidi Fredj, Algiers.
Dutta, J., Dutta, P., and Banerjee, R. (2004). Optimization
of culture parameters for extracellular protease pro-
duction from a newly isolated Pseudomonas sp. using
response surface and artificial neural network models.
Process biochemistry.
Hassan, R., Cohanim, B., De Weck, O., and Venter, G.
(2005). A comparison of particle swarm optimization
and the genetic algorithm. In Proceedings of the 1st
AIAA Multidisciplinary Design Optimization Special-
ist Conference.
Hu, X., Eberhart, R., and Shi, Y. (2003). Engineering op-
timization with particle swarm. In Proceedings of
the 2003 IEEE Swarm Intelligence Symposium, 2003.
SIS’03.
Kammoun, R., Naili, B., and Bejar, S. (2008). Applica-
tion of a statistical design to the optimization of pa-
rameters and culture medium for [alpha]-amylase pro-
duction by Aspergillus oryzae CBS 819.72 grown on
gruel (wheat grinding by-product). Bioresource tech-
nology.
Kennedy, J. (1998). The behavior of particles. In Evolu-
tionary Programming VII. Springer.
Kennedy, J., Eberhart, R., et al. (1995). Particle swarm op-
timization. In Proceedings of IEEE international con-
ference on neural networks. Piscataway, NJ: IEEE.
Kennedy, M. and Krouse, D. (1999). Strategies for im-
proving fermentation medium performance: a review.
Journal of Industrial Microbiology and Biotechnol-
ogy.
Kunamneni, A. and Singh, S. (2005). Response surface op-
timization of enzymatic hydrolysis of maize starch for
higher glucose production. Biochemical Engineering
Journal.
Shi, Y. and Eberhart, R. (1998). Parameter selection in par-
ticle swarm optimization. In Evolutionary Program-
ming VII. Springer.
Ustok, F., Tari, C., and Gogus, N. (2007). Solid-state
production of polygalacturonase by Aspergillus sojae
ATCC 20235. Journal of biotechnology.
Wilson, D., Irwin, G., and Lightbody, G. (1999). RBF prin-
cipal manifolds for process monitoring. IEEE Trans-
actions on Neural Networks.
BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms
292
