A PIEZOELECTRIC ACTUATOR,

BASED ON A LANGEVIN-TYPE TRANSDUCER,

FOR DERMATOLOGICAL AESTHETIC APPLICATIONS

Nicola Lamberti

Dip. di Ingegneria dell’Informazione e Ingegneria Elettrica, Università di Salerno, Fisciano (SA), Italy

Keywords: Piezoelectric Actuators, Langevin Transducers, Dermatological Aesthetic, Vibrating Foils, FEM.

Abstract: In dermatological aesthetic piezoelectric actuators are widely used: the skin treatment is obtained by the

bending vibration, along the length, of a steel foil with a thickness of about 0.5 mm; the vibration frequency

is in the ultrasonic range, to avoid annoying noise. In this paper a piezoelectric actuator able to excite a

bending motion in the steel foil is described; the active part of the actuator is a piezoelectric Langevin–type

transducer soliciting the foil at one edge. The actuator was designed by using ANSYS with the objective to

obtain a system with high efficiency, low losses, high mechanical stiffness and low encumbrance. Best

results were obtained by means of a Langevin actuator with a stepped horn displacement amplifier, whose

total length is λ/2 at the resonance frequency; the Langevin is connected to the foil by an ad hoc support.

The ANSYS results computed in operating conditions show a well sustained bending vibration of the foil

with stress values, in all the actuator components, far from the limit value in the material.

1 INTRODUCTION

In dermatological aesthetic piezoelectric actuators

are widely used: the skin treatment is obtained by

the bending vibration, along the length, of a steel foil

with a thickness of about 0.5 mm; the vibration

frequency is in the ultrasonic range, to avoid

annoying noise. In this paper a piezoelectric actuator

able to excite a bending motion in the steel foil is

described; the active part of the actuator is a

piezoelectric Langevin–type transducer soliciting the

foil at one edge. First of all we analyzed by ANSYS

the resonance modes of the foil, in order to identify

bending modes at an ultrasonic resonance frequency.

The second step was the design of a Langevin

transducer with the same resonance frequency. By

means of analytical models we computed the

thickness of the front and back masses of a

transducer composed by 4 piezoceramic rings,

electrically connected in parallel; in order to amplify

the displacements, on the Langevin front face we

inserted a displacement amplifier realized by using a

classical stepped horn ultrasonic concentrator with

both sections one-quarter wavelength long; finally,

the connection between the foil and the displacement

amplifier is realized by means of an ad hoc prismatic

steel “support”. In order to optimize the design we

analyzed the actuator behaviour by ANSYS, with

the purpose to maximize the bending displacement

at the free edge of the foil, to minimize the stresses

in all the device and to reduce its encumbrance.

2 FOIL RESONANCE MODES

The foil resonance modes were analyzed by using

ANSYS, in order to find a bending mode at an

ultrasonic frequency; the use of the FEM is justified

by the geometry of the foil and by the choice to use

this tool for the actuator design. Due to the foil

length (45 mm) and material (steel AISI 304), its

first bending mode has a resonance frequency of

1283 Hz; obviously this vibration mode cannot be

used for the treatment because it lies in the audible

range. On the other hand, from the ANSYS modal

analysis we obtained that the first bending mode

with an ultrasonic resonance frequency is

approximately located at 25 kHz; in Fig. 1 is

reported the ANSYS simulation of the foil

displacement field computed at this frequency.

163

Lamberti N..

A PIEZOELECTRIC ACTUATOR, BASED ON A LANGEVIN-TYPE TRANSDUCER, FOR DERMATOLOGICAL AESTHETIC APPLICATIONS.

DOI: 10.5220/0003136701630167

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 163-167

ISBN: 978-989-8425-37-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

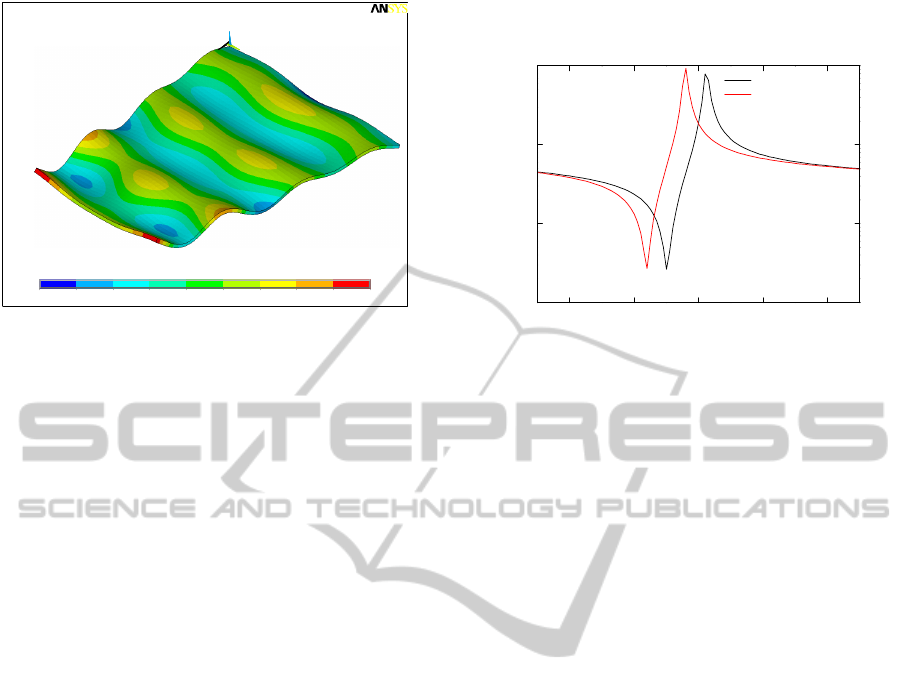
Figure 1: Foil displacement field (arbitrary units) at its

first ultrasonic bending mode (25044 Hz).

3 THE DESIGN OF THE

LANGEVIN TRANSDUCER

The Langevin transducer is basically composed of

two, or more, piezoceramic disks electrically

connected in parallel, sandwiched between two

metal masses (Langevin, 1924). It can be excited to

resonate in length–extensional mode at low

frequency, avoiding the need of high driving

voltages. The structure is usually pre stressed in

order to increase the mechanical strength of

piezoceramic elements and is suitable to absorb high

electrical power. In our case the transducer is

composed by 4 piezoceramic rings (Pz 26, by

Ferroperm Piezoceramics A/S, Kvistgaard,

Denmark) with a thickness of 1 mm, an outer

diameter of 20 mm and an inner diameter of 3.8 mm;

imposing a resonance of 25 kHz, by classical 1–D

analytical models (Zelenka, 1986) we computed that

the thickness of both the front and back steel masses

is 44.6 mm.

The 4 piezoceramic rings are electrically connect

in parallel by means of 4 copper rings (0.35 mm

thick and with the same diameters of piezoceramic

disks) placed between them. In order to verify if the

presence of the copper rings can be neglected in the

actuator design, we computed by ANSYS the

electrical input impedance Z

of the Langevin with

and without these rings; in Fig. 2 is shown the Z

amplitude computed in the two cases in a frequency

range around the foil resonance. As it can be seen,

the presence of the copper rings is not negligible: the

resonance and antiresonace frequencies both shift of

about 600 Hz (the 2.4 % of the resonance

frequency); in the next steps of the transducer design

the presence of copper contact rings must be

accounted.

Figure 2: Electrical input impedance of the Langevin

transducer computed by ANSYS taking (in red), or not (in

black) the copper contact rings into account.

In order to amplify the displacement on the

actuator front face various solutions can be used;

among these, sectional ultrasonic concentrators,

made from rods of variable and constant cross

section, are those that have been mainly exploited in

applications. Basically, sectional concentrators are

designed to resonate in length–extensional mode at

the same frequency of the Langevin transducer and

the displacement amplification depends on the ratio

between the back and the front sections. Sectional

concentrators have been widely analyzed by

Merkulov (Merkulov, 1957) and Kharitonov

(Merkulov, Kharitonov, 1959) for several shapes

(conical, exponential and catenoidal). These authors

concluded that the maximum displacement

amplification is achieved for a stepped horn, when

the two sections are both one-quarter wavelength

(λ/4) long; in this case, the amplification factor is

equal to the ratio between the areas of the two end

sections. By using this design criterion, the actuator

total length is therefore λ: λ/2 of the Langevin

transducer plus λ/2 of the stepped horn displacement

amplifier. For the design of the displacement

amplifier we just decided to use a stepped horn

device (the whole actuator is shown in Fig. 3); the

sections of the amplifier are both 48.6 mm long, the

thinner section has a diameter of 10 mm while the

other has the same diameter of the other Langevin

components.

The main problem of this kind of actuator is its

total encumbrance: in the present case the whole

length is 194.4 mm. In order to reduce the

encumbrance we designed a device whose total

length is λ/2 at the operating frequency (≈

25 kHz):

it is composed by the same 4 Pz 26 piezoceramic

X Y

-43.219

-32.941

-22.662

-12.384

-2.105

8.173

18.452

28.73

39.009

49.287

JUL 2 2010

13:07:54

NODAL SOLUTION

STEP=1

SUB =30

FREQ=25044

UZ (AVG)

RSYS=0

DMX =49.496

SMN =-43.219

SMX =49.287

22 24 26 28 30

100

1000

10000

without copper rings

with copper rings

| [Ω]

f [kHz]

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

164

rings and the same copper contacts of the λ actuator,

while the length of the two masses is 26.3 mm, and

the two sections of the displacement amplifier are 29

mm long; with this choice the actuator total

encumbrance is 116 mm, more than 40 % smaller.

Figure 3: Schematic view of the Langevin actuator with

the classical stepped horn displacement amplifier.

In order to compare the performances of the two

solutions we computed by ANSYS the vertical

component of the displacement, u

in the center of

the front face for both transducers; in Fig. 4 the |u

amplitudes computed in the two cases are compared

with |u

| computed for the Langevin without

displacement amplifier.

Figure 4: Displacement computed by ANSYS at the center

of the front face of the Langevin actuator (in black), of the

λ actuator (in red) and of the λ/2 actuator (in green).

As it can be seen the resonance frequencies are

practically the same, while the λ/2 transducer shows

a displacement amplitude a bit greater than that of

the λ one; this result within the device encumbrance

let us to prefer the λ/2 device. The only problem of

this solution is that in this case the node of u

is not

in the piezoceramic zone; this problem will be

accounted in the design of the whole actuator.

4 THE DESIGN OF THE WHOLE

ACTUATOR

In order to mechanically connect the front face of

the displacement amplifier to the vibrating foil, an

ad hoc “support” is needed. This support is a

parallelepiped whose length is equal to the radius of

the front face of the displacement amplifier, while

the width is constrained to be equal to that of the

vibrating foil. The only degree of freedom of this

element is therefore its thickness: it cannot be too

small in order to avoid flexural vibrations in the foil

in the width direction; on the other hand it cannot be

too large to don’t excessively charge the Langevin

and therefore to weaken its mechanical excitation.

By using ANSYS we designed the thickness of the

support in order to maximize the amplitude of the

flexural vibration in the foil: the best results were

obtained with a support thickness of 3 mm. In Fig. 5

is shown the geometry of the whole transducer: it is

composed by the Langevin actuator, the stepped

horn displacement amplifier, the mechanical support

and the vibrating foil.

Figure 5: Geometry of the proposed actuator.

For applications in dermatological aesthetic, the

actuator must be designed to maximize the

amplitude of the vibrations in the foil; we analyzed

the proposed actuator by ANSYS first of all to

evaluate the resonance frequency, to verify that the

displacement field in the foil is flexural and to

maximize the foil displacement. In Fig. 6 is shown

the amplitude of |u

| computed by ANSYS at the

center of the foil free edge. As it can be seen, the

maximum of the displacement is obtained at 26.1

kHz; this shift in respect to the resonance

frequencies of both the Langevin (with the

displacement amplifier) and the foil, and the ripple

in the explored frequency range are due the support

20 22 24 26 28 30

100

Langevin

λ actuator

λ/2 actuator

| [μm]

f [kHz]

SEP 11 2009

16:25:33

VOLUMES

TYPE NUM

SEP 11 2009

16:13:00

VOLUMES

VOLU NUM

Piezoceramics

Dis

lacement am

Lan

evi

A PIEZOELECTRIC ACTUATOR, BASED ON A LANGEVIN-TYPE TRANSDUCER, FOR DERMATOLOGICAL

AESTHETIC APPLICATIONS

165

and the superposition of many modes that are

strongly coupled together.

Figure 6: Amplitude of the displacement computed by

ANSYS at the centre of the foil free edge.

In order to verify if the foil vibration at the

resonance (26.1 kHz) is a flexural vibration we

computed the displacement field in the actuator at

this frequency; in Fig. 7 is shown the obtained result.

Figure 7: Displacement field (in meters) in the proposed

actuator computed at 26.1 kHz.

As it can be seen, an uniform bending vibration

is excited in the foil and the displacements have their

maximum amplitude at the unconstrained edge. The

displacements in the "Langevin" actuator are

negligible with respect to those of the foil, and

therefore a good stiffness of the whole structure is

expected.

Finally, in order to verify the stiffness of the

proposed structure, the stresses in the actuator have

been computed by supplying it at 26.1 kHz with a

sinusoidal voltage signal of 250 V in amplitude. In

Fig. 8 the field of stresses along the structure is

shown.

Figure 8: Stress field (in Pascal) computed supplying the

proposed actuator at 26.1 kHz with a sinusoidal voltage

generator of 250 V.

The weaker actuator part is the zone of contact

between foil and support; as it can be seen, only in a

small area around the centre the stress reaches a

value of about 100 MPa, whilst in the remaining

contact areas it is below 76 MPa and even sinks

below 13 MPa in the external zones; these values are

far from the yield point, of about 500 MPa in the

steel of the support and the foil. Even the stress on

the piezoelectric ceramics is small: below 15 MPa;

this avoids depolarisation problems (the

depolarization limit is 30 MPa). Finally, the

maximum of the stress on the foil doesn’t exceed

140 MPa and therefore also in this zone it is far from

the limit value in the steel.

5 CONCLUSIONS

In this paper a piezoelectric actuator able to excite a

bending motion in a steel foil is described; the active

part of the actuator is a piezoelectric Langevin–type

transducer soliciting the foil at one edge. The

resonance modes of the foil were analyzed by

ANSYS in order to identify bending modes at an

ultrasonic resonance frequency. The second step was

the design of a Langevin transducer with the same

resonance frequency: by means of ANSYS we

designed a transducer composed by 4 piezoceramic

rings, electrically connected in parallel, a front and a

back mass and a displacement amplifier realized by

means of a classical stepped horn ultrasonic

concentrator. We compared the performance of this

actuator with that of a Langevin with the same

components but with a total length equal to λ/2 at the

resonance frequency; the performance of this device

is a bit greater than that of the other, with the

advantage of an encumbrance about one half. The

22 23 24 25 26 27 28 29 30 31

100

| [

f [kHz]

-.129E-04

-.887E-05

-.487E-05

-.878E-06

.312E-05

.711E-05

.111E-04

.151E-04

.191E-04

.231E-04

JAN 29 2007

11:42:36

NODAL SOLUTI ON

STEP=1

SUB =38

FREQ=26100

REAL ONLY

UZ (AV G)

RSYS=0

DMX =.232E-0 4

SMN =-.129E- 04

SMX =.231E-0 4

155167

.153E+08

.305E+08

.457E+08

.608E+08

.760E+08

.912E+08

.106E+09

.122E+09

.137E+09

JAN 29 2007

11:31:33

NODAL SOLUTIO N

STEP=1

SUB =38

FREQ=26100

REAL ONLY

SINT (AVG )

DMX =.232E-04

SMN =155167

SMX =.137E+09

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

166

connection between the foil and the displacement

amplifier is realized by means of an ad hoc prismatic

steel “support”. The design of whole actuator was

optimized by means of ANSYS, with the purpose to

maximize the bending displacement at the free edge

of the foil. Finally, in order to test the actuator

stiffness, we computed the stresses in the structure in

operating conditions and we verified that their

values in any point are far from the material limits.

The next step will be the realization of an

actuator prototype in order to experimentally verify

its performance and to refine the design.

The actuator design criteria are the basis of an

international patent (Lamberti et al., 2008).

REFERENCES

Langevin P., French Patent n. 503913 (29/5/1929), n.

505703 (5/8/1920), n. 575435 (30/7/1924).

Zelenka J., 1986. Piezoeletric resonator and their

applications, Elsevier, New York.

Merkulov L. G., 1957, Design of ultrasonic concentrators.

In Sov. Phys. Acoust., 3, pp. 246–255.

Merkulov L. G., Kharitonov A. V., 1959, Theory and

analysis of sectional concentrators. In Sov. Phys.

Acoust., 5, pp. 183–190.

Lamberti N., Casacchia G., Ardia L., Caputo A., 2008,

Actuator with interchangeable bending-vibrating foils,

based on a langevin-type transducer, International

Patent, PCT/IT2008/000431.

A PIEZOELECTRIC ACTUATOR, BASED ON A LANGEVIN-TYPE TRANSDUCER, FOR DERMATOLOGICAL

AESTHETIC APPLICATIONS

167