A BAYESIAN METHOD FOR THE DETECTION OF EPISTASIS

IN QUANTITATIVE TRAIT LOCI

USING MARKOV CHAIN MONTE CARLO MODEL COMPOSITION

WITH RESTRICTED MODEL SPACES

Edward L. Boone

Department of Statistical Science and Operations Research, Virginia Commonwealth University, Richmond, Virginia, U.S.A.

Susan J. Simmons

, Karl Ricanek

Department of Mathematics and Statistics,

Department of Computer Science, University of North Carolina Wilmington

Wilmington, North Carolina, U.S.A.

Keywords:

Quantitative trait loci, Epistasis, Bayesian statistics, Markov chain Monte Carlo model composition.

Abstract:

Epistasis or the interaction between loci on a genome is of great interest to geneticists. Herein, a powerful

Bayesian method utilizing Markov chain Monte Carlo model composition approach using restricted spaces is

developed for identifying epistatic effects in Recombinant Inbred Lines (RIL). The method is veriﬁed through

a simulation study and applied to an Arabidopsis thaliana data set with cotyledon as the quantitative trait.

1 INTRODUCTION

Quantitative Trait Loci (QTL) analysis is concerned

with determining which region on a genome that ex-

plains or controls a quantitative trait. However, in

many instances an iteraction between regions or loci

may provide a better explanation for a trait than re-

gions having a strictly additive inﬂuence. This inter-

action between loci on a genome is known as epista-

sis. To study QTLs, organisms generated by recombi-

nant inbreeding are often used. Recombinant Inbred

Lines (RIL) are organisms that have been repeatedly

mated with siblings and themselves in order to create

a inbred line whose genetic structure is a combination

of the original parent organisms. These RILs provide

a mechanism to reduce environmental and individual

effects. Furthermore, these homozygous organisms

help simplify the search for the loci on the genome

has inﬂuence over a trait. This simpliﬁcation is due

to fact that at each locus one does not need to know

the actual allele. Instead, one can track whether the

allele at a locus came from parent A or parent B. For

a complete review of RILs see (Broman, 2005).

Several methods have been developed to detect

and evaluate epistatic effects for continuous traits.

Multiple Interval Mapping (MIM) proposed by (Kao

et al., 1999) based on ﬁtting a multiple regression

model that has both main effect terms as well as

interactions and employing a non-Bayesian search

method. (Carlborg, 2004) use a genetic algorithm

to search for the loci and epistatic effects. (Hansen

and Wagner, 2001) propose a theoretical framework

for higher order interactions. (Kao and Zeng, 2001)

use the framework of (Cockerham, 1954) to partition

the variance for known main and epistatic effects in

order to understand the contribution of each with no

search method. (Zeng et al., 2005) and (Wang and

Zeng, 2006) use (Cockerham, 1954) partition the vari-

ance when epistatic effects with multiple alleles are

present however no search method is presented in this

work either. (Hanlon and Lornez, 2005) use an op-

timization approach to ﬁnd combinations of epistatic

effects that best represent the trait of interest based on

squared error distance.

To avoid this problem of model selection (Broman

and Speed, 2002) use Markov Chain Monte Carlo

Model Composition (MC

) to search for the main

effects (additive models) that contribute to the trait.

This procedure is a variant of reversible jump Markov

chain Monte Carlo by (Green, 1995). (Boone et al.,

L. Boone E., J. Simmons S. and Ricanek K..

A BAYESIAN METHOD FOR THE DETECTION OF EPISTASIS IN QUANTITATIVE TRAIT LOCI USING MARKOV CHAIN MONTE CARLO MODEL

COMPOSITION WITH RESTRICTED MODEL SPACES.

DOI: 10.5220/0003139200710078

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 71-78

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

2006) extend this to restricted model spaces to allow

for more loci than observations. (Yi et al., 2003), (Yi

et al., 2005), (Yi et al., 2007a), (Yi et al., 2007b) use

the MC

framework with various restrictions on the

model space to search for main and epistatic effects.

However, (Yi et al., 2003), (Yi et al., 2005), (Yi et

al., 2007a), (Yi et al., 2007b) and the R/qtlbim soft-

ware of (Yandell et al., 2007) do not require that the

main effect terms corresponding to the epistatic ef-

fects be present in the model. Furthermore, (Broman

and Speed, 2002), (Yi et al., 2003), (Yi et al., 2005),

(Yi et al., 2007a), (Yi et al., 2007b) and (Yandell et

al., 2007) employ information criteria such as AIC or

BIC as the basis for the MC

search. (Boone et al.,

2005) show that while BIC is an asymptotically cor-

rect approximation for posterior model probabilities,

in the low to moderate sample size case BIC performs

poorly.

The goal of this work is to explore a MC

algo-

rithm with restricted model spaces that require the

main effect terms corresponding to the epistatic be

present in the model. In addition, this article proposes

conditional activation probabilities as a tool to evalu-

ate epistatic effects in models where the correspond-

ing main effects are included. Furthermore, to avoid

the use of information criterion such as AIC or BIC

as the basis of the MC

search.

Current methods for assessing epistasis use fre-

qentist tests which are inherently model dependent.

This work uses activation probabilities (proposed by

(Boone et al., 2006) for use in QTLs), deﬁned in Sec-

tion 2.2 for each of the main and epistatic effects to

determine the marginal posterior probability of each

effect regardless of which model is chosen. Figure 1

shows an example heatmap of the activation probabil-

ities that may occur when epistasis is present. Activa-

tion probabilities along the diagonal correspond to the

main effect of the locus. The off diagonal activation

probabilities correspond to epistatic effects. Notice

that by looking along the diagonal the main effects

appear to be at locus 12, locus 26 and locus 35 as

the (12,12), (26, 26) and (35,35) regions have high

probability. Furthermore one can look at the off di-

agonal and see that loci 12 and 26 appear to have an

epistatic effect as well as noted by high probability in

the (12,26) region. However, loci 12 and 35 and loci

26 and 35 do not appear to have an epistatic effect due

to low probability in the regions common to (12,35)

and (26,35) on the heatmap.

Section 2 deﬁnes the model, basic search strat-

egy, activation probabilities and conditional activation

probabilities. Section 2.3 explains the neighborhood

deﬁnition and search strategy under restricted model

spaces. Section 3 gives a simulation study showing

0.0

0.2

0.4

0.6

0.8

1.0

5 10 15 20 25 30 35

Locus

Figure 1: Simulated heatmap of activation probabilities for

main effect and epistatic effects. Activation probabilities

along the diagonal correspond to main effects and off diag-

onal correspond to epistatic effects.

the efﬁcacy of the method for detecting both main ef-

fects and two-way interaction effects. Section 4 con-

siders the Arabidopsis Thaliana as an example. The

dataset for this model organism has 158 lines of RIL

and 38 markers (loci) and cotelydon opening angle is

the quantitative trait of interest.

2 BAYESIAN MODEL SEARCH

2.1 Model Deﬁnition

Let y

be the quantitative trait for the i

observation.

For eahc of the p loci l

,...,l

the parentage of the

allele is recorded as A if the allele came from parent

A and B if the allele came from parent B. However,

in some instances the allele is not determined which

needed to be reﬂected in the analysis. For the i

ob-

servation and locus l

this information can be coded

into X

as:







1, allele l

is from parent A

−1, allele l

is from parent B

0, allele l

is undetermined

(1)

Here the X

correspond to the main effects. For the

epistatic effects (two-way interaction) this produces

the interaction between loci l

and l

as:







1, alleles l

and l

from same parent

−1, alleles l

and l

from different parents

0, allele l

or l

is undetermined

(2)

Using a traditional ﬁrst order model with a two-

way multiplicative interaction terms the model is de-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

ﬁned as:

= µ+

∑

j=1

) +

∑

k< j

) + ε

(3)

where ε

∼ N(0,σ

), P

is the set of loci l

model M

, and I

is an indicator function that takes

the value 1 if l

∈ P

and 0 otherwise. Here β

cor-

responds to the main effect of locus l

and β

is the

epistatic effect between loci l

and l

2.2 Bayesian Model Averaging

In a model space M with |M | models, the posterior

probability of model M

given the data D can be com-

puted via Bayes’ Theorem:

P(M

|D ) =

P(M

)P(D |M

)

∑

|M |

t=1

P(M

)P(D |M

)

. (4)

The marginal probability of the data D given model

, P(D |M

) is involved in computing (4) and can be

calculated using:

P(D |M

) =

P(θ

)P(D |θ

)dθ

, (5)

where θ

is the parameter vector corresponding to

model M

. Evaluating the integral in (5) can be com-

plicated. Approximations such as the Laplace ap-

proximation and the approximationbased on Schwarz

Bayesian Information Criterion (BIC) could be em-

ployed. However, in the linear model case, as in equa-

tion (3), where the coefﬁcient vector for model M

∼ N(µ

) and σ

∼ Inv−χ

(ν,λ) prior is used,

an analytic expression for (5) is:

P(D |µ

,ν,X

) =



ν+n



(νλ)





|I + X

′

1/2

× [λν+ (Y −X

)

′

× (I + X

′

)

−1

× (Y −X

)]

−

ν+n

, (6)

where µ

and V

are the mean and variance, respec-

tively, and ν and λ are the degrees of freedom, and lo-

cation parameter, respectively. This work will employ

(6) for computing (5) versus any information criterion

based approximations.

In cases where the model space is sufﬁciently

large, calculating (5) for each model is computation-

ally infeasible. A stochastic search through the model

space can be performed using a metropolis-hastings

approach. For more on metropolis-hastings sampling

see (Chib and Greenberg, 1995), (Bolstad, 2010).

This can be accomplished by constructing neighbor-

hoods around the current model M

. Typically, the

neighborhoods nbd(M

) consist of all models with

one additional term than model M

and all models

with one less term than model M

. For a candidate

model M

∈nbd(M

) the probability, α, of acceptance

of model M

is given by.

α = min



P(M

)P(D |M

)

P(M

)P(D |M

)

q(M

)

q(M

)



, (7)

where q(M

) is the probability that the candidate

model is M

is selected for consideration given the

current state is model M

. Note the neighborhood

structure mentioned above is not appropriate when

the main effect terms are required to be in the model

whenever an epistatic term is in the model. (Yi et al.,

2003), (Yi et al., 2005), (Yi et al., 2007a), (Yi et al.,

2007b) and (Yandell et al., 2007) allow the neighbor-

hood to be all models with one main effect term more

or less than M

and all models with one epistatic effect

more or less than M

. Since they do not require than

when an epistatic term is in the model that the corre-

sponding main effect terms be in the model as well,

this is a reasonable neighborhood structure however

it is different than the structure proposed here. They

also further propose that the neighborhoods could in-

clude only loci that are near to current locus on the

genome.

Once the posterior model probabilities have been

computed activation probabilities can be used to as-

sess the impact of predictor X

and can be computed

via:

P(β

6= 0|D ) =

|M |

∑

c=1

P(β

6= 0|D ,M

)P(M

|D ). (8)

Activation probabilities are different from the tradi-

tional p-value in that largevaluesindicate signiﬁcance

versus small values. In addition, activation probabili-

ties do not depend on a speciﬁc model as do p-values.

The activation probabilities can be calculated via MC

as deﬁned in section 2.3.

Activation probabilities will have a problem de-

tecting two-way interactions when the main effect

terms are required to be in the model in order for the

two-way interaction term to be present. This induces

the following inequalities:

P(β

|D ) ≤ P(β

|D ) (9)

P(β

|D ) ≤ P(β

|D ).

Hence, using the standard activation probabilities for

two-way interaction effects will produce probabilities

that are damped. In order to amplify the activation

probabilities of the two-way interaction effects one

A BAYESIAN METHOD FOR THE DETECTION OF EPISTASIS IN QUANTITATIVE TRAIT LOCI USING

MARKOV CHAIN MONTE CARLO MODEL COMPOSITION WITH RESTRICTED MODEL SPACES

can use conditional activation probabilities. Condi-

tional activation probabilities can also be obtained by:

P(β

6= 0|β

6= 0,β

6= 0,D ) (10)

P(β

6= 0,β

6= 0|D )

P(β

6= 0,β

6= 0|D )

provided that P(β

6= 0,β

6= 0|D ) > 0. In practice

one should only consider conditional activation prob-

abilities when both P(β

|D ) and P(β

|D ) are consid-

erably large. In cases where P(β

|D ) or P(β

|D ) are

small then unreasonably large inﬂations to the condi-

tional activation probabilities will occur and hence the

result in incorrect inferences.

2.3 Restricted Model Space

A simple approach to deﬁning the neighborhoods of

a model M

is to include all models that add an ad-

ditional term or drop an existing term. However, this

violates a model that require both main effect terms

need to be present in the model in order for the cor-

responding two-way interaction to be added. Further-

more, the model need not contain all interaction terms

possible. Notice this creates a large model space.

For the ﬁrst order models with p predictors the size

of the model space is 2

. However with the addi-

tion of interaction terms, the size grows considerably

more. In a dataset with 30 loci, a full model with all

ﬁrst order terms and two-way interaction terms will

have 465 terms. This can be prohibitively large for

most datasets and algorithms. If the model space is

restricted to r < p predictors and the corresponding

epistasis terms, then any model considered will not

have nearly as many terms. If r is chosen wisely, then

the researcher can ensure that each model under con-

sideration has sufﬁcient degrees of freedom to be es-

timated.

Furthermore, cases where linear dependencies ex-

ist among the predictors estimation can be compli-

cated. One approach to address this issue is to assign

P(M

) = 0 to all models where linear dependencies

exist among the predictors. Hence removing all mul-

ticollinear models from consideration. Any time there

are multicollinear terms an index will need to be cre-

ated in order to keep track of any aliased terms. This

aliasing can cause problems when there is a large ef-

fect size for the aliased terms.

The use of restricted model spaces allows for the

assessment of all candidate variables, however it re-

stricts the number of candidate variables that may be

simultaneously considered in a single model. (Yi et

al., 2003), (Yi et al., 2005), (Yi et al., 2007a), (Yi et

al., 2007b) and (Yandell et al., 2007) use two restric-

tions one for the number of main effect terms and one

for the number of epistatic terms allowed in the model

simultaneously. They also give a simple guideline to

determine the size of each restriciton. They suggest

to choose the restriction r = m+ 2

√

m where m is the

a priori expected number of main effects. Similarly

the same formula can be employed where m is the ex-

pected number of epistatic effect.

To search through the restricted model space,

can be employed using equation (7). Note that

q(M

) must be determined to move through the

sample space. Let nbd(M

) be all models with one

main effect term more, one valid interaction term

more, one main effect term less and one interaction

term less than model M

. Denote adding a main ef-

fect term as AMT, adding an interaction effect term as

AIT, dropping a main effect term as DMT and drop-

ping an interaction effct term as DIT. The probility of

each of these actions depends on the attributes of the

current model M

. Let γ

and φ

be the number of

main effect terms and number of interaction terms in

, respectively. In order to ensure that all models

in nbd(M

) are equally likely, the probability of each

action, AMT, AIT, DMT and DIT need to be deter-

mined. Let Ω = {AMT, AIT,DMT,DIT} be an action

space. Once these probabilities have been calculated,

the following procedure allows for each of the models

in nbd(M

) to be sampled to be candidate model. First

determine, P(AMT), P(AIT), P(DMT) and P(DIT),

and choose an action with the corresponding proba-

bility. Then select with equal probability a model that

is in nbd(M

) and corresponds to the action. This pro-

cedure ensures that all models in nbd(M

) have equal

probability. Having all models in nbd(M

) equally

likely will be necessary in computing q(M

For γ

= 0, only a main effect term may be added

since no interaction terms are in the model. Hence the

probability distribution for Ω is:

P(AMT) = 1, P(DMT) = 0,

P(AIT) = 0,P(DIT) = 0. (11)

For γ

= 1, the one of the p−1 main effect terms

not in the model may be added or the one main effect

term in the model may be droped and no interaction

terms are allowed in this model. Hence the probabil-

ity distribution for Ω is:

P(AMT) =

p−1

,P(DMT) =

P(AIT) = 0,P(DIT) = 0. (12)

For 2 ≤ γ

≤ r, no restrictions are involved.

Hence, all actions in Ω are allowed. Hence, the prob-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

ability distribution for Ω is:

P(AMT) =

p−γ

, P(AIT) =

−φ

P(DMT) =

, P(DIT) =

(13)

For γ

= r, due to the restriction that no more than

r main effect terms may be in a model at a single time,

no main effect terms may be added. However, main

effect terms may be dropped and interaction terms

may be added or dropped. Hence, the probability dis-

tribution for Ω is:

P(AMT) = 0, P(AIT) =





−φ





+ k

P(DMT) =





+ r

,P(DIT) =





+ r

.(14)

Since each model in nbd(M

) is equally likely

to be sampled, q(M

) can easily be formed. For

example, let M

and M

be such that γ

= γ

+ 1

where γ

< r and γ

> 2. Then this corresponds

to the action AMT and the probability of candi-

date model M

given that the current model is M

is one out of the number of models in nbd(M

speciﬁcally, q(M

) =





−1

and simi-

larly q(M

) =





−1

. Hence the ratio of

the probability of candidate models for this case is:

q(M

)

q(M

)









3 SIMULATION STUDY

To validate this approach, loci information from Ara-

bidopsis thaliana Bay-0 × Shadara was used. Fig-

ure 2 illustrates the genetic map of the Arabidopsis

thaliana Bay-0 × Shadara,which has ﬁve chromo-

somes and on each chromosome each locus where the

parentage of the allele has been determined is marked.

There was a total of 38 loci used for this simulation

study and 158 lines.

To assess the ability of the method to detect both

main effects and epistatic effects a simulation study

Figure 2: Genetic map of the Arabidopsis Thaliana Bay-0

by Shadara.

was conducted. Using the loci matrix from the Ara-

bidopsis thaliana dataset two loci X

and X

were ran-

domly selected from the possible loci and the follow-

ing model was used to generate the data:

= δX

+ δX

+ ε

, (15)

where δ is the effect size, ε

∼ N(0, 1). Each dataset

contained a sample size of 158 observations. Effect

sizes of 0, 1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2 and 5

were considered. Each of these effect sizes was re-

peated 10 times.

Using the data set and the method proposed the

following probabilties were calculated: P(X

|D ),

P(X

|D ), P(X

|D ) and P(X

,D). These

were calculated for 100 simulated data sets. Using

the following prior distributions β

∼ N(0,200) and

∼ χ

(1) for the model parameters and P(M

) is

uniform over the all models subject to the restric-

tion of r = 10. For each simulated data set a chain

of 16,000 samples were taken from the posterior dis-

tribution of the models, with the ﬁrst 1,000 samples

discarded as burn-in samples. The activation prob-

abilities were calculated using the remaining 15,000

samples.

Figure 3 show boxplots the main effect activation

probabilities versus the effect size from the simulated

datasets. Notice that for effect sizes of 0 and 1/2

the activation probabilities are low indicating that not

much evidence exists for the main effect at that locus.

However, for effect sizes at and above 1 the activa-

tion probabilites are quite high, typically above 0.8.

It should be noted that activation probabilities are not

associated with the idea of a p-value and hence can-

not be interpreted as such. Furthermore, the choice

of cutoff values for activation probabilities and what

is deemed statistically signiﬁcant, in the Type I and

Type II error sense, has not been studied. However,

we should notice that the activation probabilities for

effect sizes at and above 1 are much larger than those

when the effect size is 0. Hence, one could feel con-

A BAYESIAN METHOD FOR THE DETECTION OF EPISTASIS IN QUANTITATIVE TRAIT LOCI USING

MARKOV CHAIN MONTE CARLO MODEL COMPOSITION WITH RESTRICTED MODEL SPACES

ﬁdent that the locus is important for inﬂuencing the

observed trait.

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

0.0 0.2 0.4 0.6 0.8 1.0

Effect Size

Activation Probabilities

Figure 3: Boxplots of main effect activation probabilities

for effect sizes 0, 1/2, 1, 3/2, 2, 5/2, 3, 7/2, 4, 9/2 and 5

using simulated data sets.

Figure 4 show boxplots for activation probabili-

ties of the epistatic effects and the conditional activa-

tion probabilities for epistatic effects versus the effect

size. Notice that in both plots that both the activa-

tion probabilities and the conditional activation prob-

abilities are low for effect sizes 0 and 1/2 indicating

that the epistatic effect of the two loci have no mini-

mal effect on the observed trait. However, notice that

for effect sizes larger than 1 the conditional activation

probabilities are considerably higher than the stan-

dard activation probabilities. Again there has been no

studies of cutoff values for activation probabilities nor

conditional activation probabilities. Looking at both

the activation probabilities and conditional activation

probabilities with reference to effect size 0 one could

feel conﬁdent that the two loci work in combination

to inﬂuence the observed trait.

0 0.5 1 2 4

0.0 0.2 0.4 0.6 0.8

Effect Size

Activation Probability

0 0.5 1 2 4

0.0 0.2 0.4 0.6 0.8

Effect Size

Conditional Activation Probability

Figure 4: Boxplots of epistatic effect activation proba-

bilities (left) and conditional activation probabilities for

epistatic effects (right) for effect sizes 0, 1/2, 1, 3/2, 2,

5/2, 3, 7/2, 4, 9/2 and 5 using 100 simulated data sets per

effect size. Dashed line at 1/2 is for reference.

4 EXAMPLE

The Arabidopsis thaliana is a model plant for genetic

experiments in that it is easily genetically manipu-

lated. The response of interest is the angle cotyledon

opening for 158 lines; the values range between 0 and

180. The cotyledon is the is the ﬁrst embryonic leaves

on a seedling plant. The wider the opening angle the

more viable the mature plant.For each line at each of

the chromosomal locations (markers) a value of 1 or -

1 corresponding to whether the marker at that location

came from parent A or parent B, respectively. With

this data and using an unrestricted model space the

largest model would have 741 terms. Hence, many

models are not able to be ﬁt. By restricting the model

space to r = 10 the largest model would have 55 terms

and thus, all models have enough observations to be

estimated.

To determine if any aliasing between the main

effects and interaction terms occured the data was

screened. This screening showed that no interaction

terms are aliased with any main effect term. Hence,

conclusions about the main effect terms will not be

confounded with any epistatic effects. An additional

screen of the data was performed to determine if there

is aliasing between any interaction effects. Aliased in-

teraction effects were noted for consideration during

posterior inferences.

For this example, the exact marginal posterior

probability of the data given model M

was computed

using equation (6) and the proposed MC

method with

restricted model space was utilized. For each model

under consideration the prior distributions for the

model parameters were deﬁned as: β

∼ N(0,200)

for all j and β

∼ N(0,200) for all interaction terms

jk in model i; for σ

, λ = 1 and ν = 1 are used. Note

that when ν = 1 the Inv −χ

has inﬁnite mean and

variance. Hence, should be relatively uninformative.

For each model M

where multicollinearity does not

occur, the prior probability P(M

) is chosen uniform

across this space. Thus, a priori, no model is preferred

over another.

Using the restriction r = 10, 25 chains of 11,000

were run with a burn in of 1,000 samples using

overdispersed starting models resulting in 250,000

samples. The number of visits to model M

was

recorded and the probability of model given the data

P(M

|D) is estimated as the number of visits to model

divided by the length of the chain. The proba-

bilities appeared to converge after 15 chains, indicat-

ing convergence. Using these probabilities the activa-

tion probabilities P(β

6= 0|D ) are computed for each

main and epistatic effect. Figure 5 shows a heat map

of epistatic probabilities. Notice that the highest acti-

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

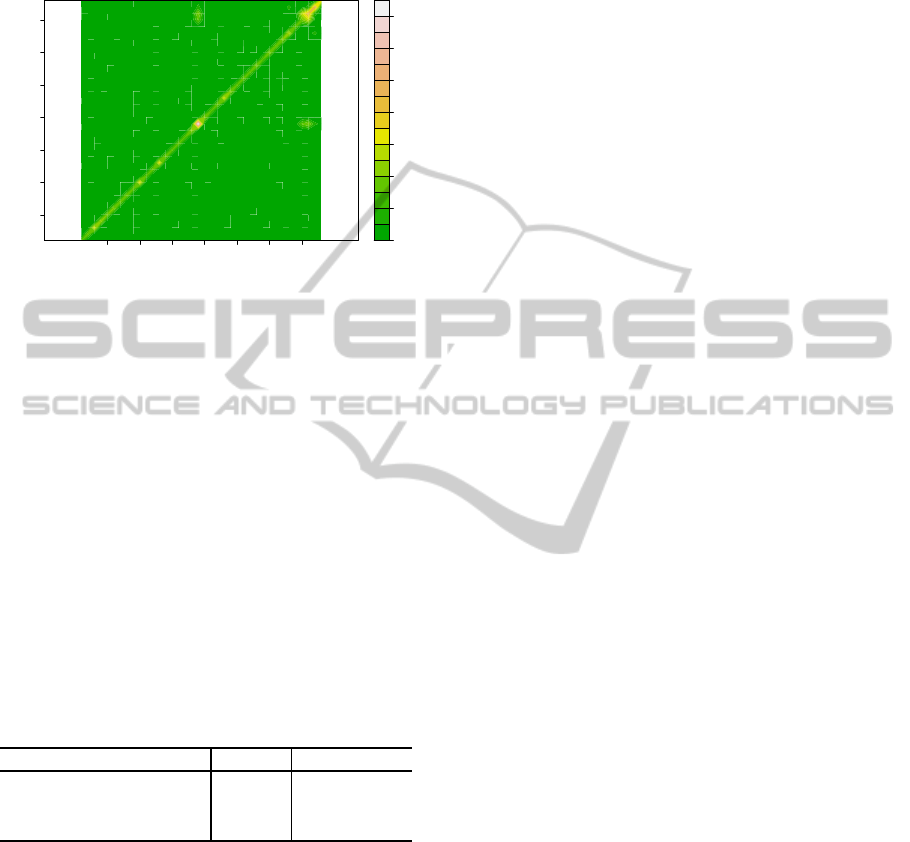
vation probability locus on the heat map is at locus 18

(ATHCHIB2) and no epistatic, off diagonal, effects

have high activation probability.

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

5 10 15 20 25 30 35

Locus

Figure 5: Heat map of epistatic probabilities.

The activation probabilities for the 3 highest

loci, ATHCHIB2, MSAT5-9 and MSAT5-22 are as

follows: P(ATHCHIB2|D ) = 0.741, P(MSAT5 −

9|D ) = 0.481 and P(MSAT5 − 22|D ) = 0.445.

This suggests that the following epistatic effects

should be considered: ATHCHIB2 × MSAT5 −

9, ATHCHIB2 × MSAT5 − 22 and MSAT5 −

9 × MSAT5 − 22. Previous studies have shown

ATHCHIB2 to be a locus associated with cotely-

don opening (Boone et al., 2006). Hence the re-

sults agree with biological expectations. In order to

more accurately locate the locus associated with cote-

lydon opening a dense map of genes near ATHCHIB2

should be undertaken.

Table 1: Activation probabilities and conditional activation

probabilities of epistatic effects between locus l

and locus

P(l

|D ) P(l

,D )

ATHCHIB2 MSAT5-9 0.070 0.243

ATHCHIB2 MSAT5-22 0.061 0.191

MSAT5-9 MSAT5-22 0.062 0.135

5 DISCUSSION

The proposed method for detecting epistasis has the

ability to determine which main effects as well as

which two-way interaction effects are present in a

dataset as evidenced by the simulation study. The

method was applied to the Arabidopsis thaliana data

and no epistatic effects were found with respect to

cotyledon opening angle. However, the known lo-

cus for controlling cotyledon opening was detected,

ATHCHIB2. The search method was employed in a

situation where the number of parameters in the full

model far exceeded the number of observations. The

search was done in a manner that allowed for sufﬁ-

cient degrees of freedom for each model under con-

sideration.

A study of epistatic models which do not require

the ﬁrst order terms to be present should be consid-

ered as well. This may allow for better detection of

epistatic effects as the model search does not need to

ﬁrst add a main effect in order to later include the

epistatic term. In this case the model space would

be reduced by 2

models. However, if all other in-

teraction terms are equally likely to be added to the

model, the Metropolis-Hastings step may have low

acceptance probability and convergence of the MC

algorithm may be slow. In addition, any loci that have

effects that are not in interaction with other loci may

not be detected. Hence, reducing the utility of the

method.

Caution should be used when using restricted

model spaces. The method works best when it is be-

lieved that only a few loci control the trait of interest.

In cases where it is believed that a large number of

loci control the trait of interest, especially when this

exceeds the restriction on the model space, then the

search method maybe come very ineffective at assess-

ing both the main effect as well as the epstatic effects.

Since the models at the restriction boundary will have

high posterior model probabilites it may be difﬁcult

to move through regions of lower probability towards

even more probable models. In most cases in genetics

it is believed that only a few loci control the trait of

interest.

REFERENCES

Broman, K. W. (2005) The Genomes of Recombinant In-

bred Lines Genetics, 169, 1133-1146.

Broman, K. W. and Speed, T. P. (2002) A model selection

approach for the identiﬁcation of quantitative trait loci

in experimental crosses. J.R. Statist. Soc. B, 64, 641-

656.

Bolstad, W. M. (2010) Understanding Computational

Bayesian Statistics. John Wiley, New York. ISBN 0-

470-04609-8

Boone, E. L., Ye, K. and Smith, E. P. (2005) Assessment of

two approximation methods for computing posterior

model probabilities. Computational Statistics & Data

Analysis, 48, 221-234.

Boone, E. L., Simmons, S. J., Ye, K., Stapleton, A. E.

(2006) Analyzing quantitative trait loci for the Ara-

bidopsis thaliana using Markov chain monte carlo

model composition with restricted and unrestricted

model spaces. Statistical Methodology, 3, 69-78.

A BAYESIAN METHOD FOR THE DETECTION OF EPISTASIS IN QUANTITATIVE TRAIT LOCI USING

MARKOV CHAIN MONTE CARLO MODEL COMPOSITION WITH RESTRICTED MODEL SPACES

Carlborg, O., Andersson, L. and Kinghorn, B. (2000) The

Use of a Genetic Algorithm for Simultaneous Map-

ping of Multiple Interacting Quantitative Trait Loci

Genetics, 155, 2003-2010.

Chib, S. and Greenberg, E. (1995) Understanding the

MetropolisHastings Algorithm. American Statisti-

cian, 49, 327335.

Cockerham, C. (1954) An extension of the concept of parti-

tioning hereditary variance for the analysis of covari-

ances among relatives when epistasis is present. Ge-

netics, 39, 859-882.

Green, P. J. (1995) Reversible jump Markov chain Monte

Carlo computation and Bayesian model determina-

tion. Biometrika, 82, 711-732.

Hanlon, P. and Lorenz, A. (2005) A computational method

to detect epistatic effects contributing to a quantitative

trait. J. Thoer. Biol., 235, 350-364.

Hansen,T. F. and Wagner, G. P. (2001) Modeling genetic

architecture : a multilinear theory of gene interaction.

Theor. Popul. Biol, 59, 61-86.

Kao, C. H., Zeng, Z. B. and Teasdale, R. D. (1999) Multiple

Interval Mapping for Quantitative Trait Loci. Genet-

ics, 152, 1203-1216.

Kao, C. H. and Zeng, Z-B. (2002) Modeling Epistasis

of Quantitative Trait Loci Using Cockerham’s Model.

Genetics, 160, 1243-1261.

Wang, T. and Zeng, Z.-B. (2006) Models and partition of

varieance for quantitative trait loci with epistasis and

linkage disequilibrium. BMC Genetics, 7, 9.

Yandell, B. S., Mehta, T., Samprit, B., Shriner, D.,

Venkataraman, R., Moon, J. Y., Neeley, W. W., Wu,

H., von Smith, R. and Yi, N. (2007) R/qtlbim:

QTL with Bayesian Interval Mapping in experimen-

tal crosses. Bioinformatics, 23, 641-643.

Yi, N., Xu, S. and Allison D. B. (2003) Bayesian Model

Choice and Search Strategies for Mapping Interacting

Quantitative Trait Loci Genetics, 165, 867-883.

Yi, N., Yandell, B. S., Churchill, G. A., Allison, D. B.,

Eisen, E. J., and Pomp, D. (2005) Bayesian model

selection for genome-wide epistatic quantitative trait

loci analysis. Genetics, 170, 1333-1344.

Yi, N., Samprit, B., Pomp, D. and Yandell, B. S. (2007)

Bayesian Mapping of Genomewide Interacting Quan-

titative Trait Loci for Ordinal Traits Genetics, 176,

1855-1864.

Yi, N., Shriner, D., Samprit, B., Mehta, T., Pomp, D. and

Yandell, B. S. (2007) An efﬁcient Bayesian model se-

lection approach for interacting quantitative trait loci

models with many effects. Genetics, 176, 1865-1877.

Zeng, Z-B., Wang, T. and Zou, W. (2005) Modeling quanti-

tative trait loci and interpretation of models. Genetics,

169, 1711-1725.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence