FEATURE INDUCTION OF LINEAR-CHAIN CONDITIONAL

RANDOM FIELDS

A Study based on a Simulation

Dapeng Zhang and Bernhard Nebel

Department of Computer Science, University of Freiburg, Georges-Khler-Allee Geb. 52, Baden-Wrttemberg, Germany

Keywords:

Conditional random ﬁelds, CRF queue, Feature induction.

Abstract:

Conditional Random Fields (CRFs) is a probabilistic framework for labeling sequential data. Several ap-

proaches were developed to automatically induce features for CRFs. They have been successfully applied in

real-world applications, e.g. in natural language processing. The work described in this paper was originally

motivated by processing the sequence data of table soccer games. As labeling such data is very time consum-

ing, we developed a sequence generator (simulation), which creates an extra phase to explore several basic

issues of the feature induction of linear-chain CRFs. First, we generated data sets with different conﬁgurations

of overlapped and conjunct atomic features, and discussed how these factors affect the induction. Then, a

reduction step was integrated into the induction which maintained the prediction accuracy and saved the com-

putational power. Finally, we developed an approach which consists of a queue of CRFs. The experiments

show that the CRF queue achieves better results on the data sets in all the conﬁgurations.

1 INTRODUCTION

In natural language processing, a sentence (a se-

quence of words) needs to be “understood” by a com-

puter. An important task is to label the phrases with

e.g. noun, verb, or preposition in the sentences, map-

ping the segments of the words to the labels. In

robotics, agents are equipped with sensors in order

to acquire the environment using measurements of

the surroundings. The task of labeling is to iden-

tify the states according to the temporal sensor data.

The states are normally encoded in a vector of vari-

ables with discrete values. Similar applications can

be found in image processing and in computational

genetics.

Researchers have developed several approaches

for the sequential labeling tasks. Hidden Markov

Models (HMMs), for example, is a well-developed

generative model suitable for such a task. The infer-

ence of HMMs is based upon joint probabilities (Ra-

biner, 1990). Compared to HMMs, Conditional Ran-

dom Fields (CRFs) has a shorter history. It was ﬁrst

proposed by (Lafferty et al., 2001), then gained pop-

ularity quickly. CRFs is a discriminative model based

on conditioned probabilities. In CRFs, a hidden label

is globally conditioned on all the observations in the

sequence. CRFs outperformed HMMs in the experi-

ments on the benchmarks in natural language process-

ing (Lafferty et al., 2001).

Feature induction of CRFs was ﬁrst introduced

by (McCallum, 2003). As training CRFs requires

considerable computational power, the induction is

mainly about how to deﬁne some more efﬁcient eval-

uations for incrementally inducing the feature func-

tions of CRFs. The method of McCallum was tested

on name entity recognition and noun phrases segmen-

tation. It resulted in comparable prediction accuracy

to the approaches other than CRFs(McCallum, 2003).

There are a few further works on the topic. In (Diet-

terich et al., 2004), the boosting algorithm is embod-

ied for simultaneously inducing features and training

CRFs. All these works experimented on the same

synthetic data, which served as a testbed for the com-

parison.

Our research was originally motivated by the ex-

planation of the data of table soccer games. The

sequential game data is made available via a game

recorder (Zhang and Hornung, 2008). The labels are

the actions of human players e.g. lock, attack, block,

pass, and dribble. These data considerablly differ

from the synthetic data used by the authors mentioned

above. At each time slice, the measurements are en-

coded in a vector of Boolean variables. Each skill

of human players consists of hundreds of such time

230

Zhang D. and Nebel B..

FEATURE INDUCTION OF LINEAR-CHAIN CONDITIONAL RANDOM FIELDS - A Study based on a Simulation.

DOI: 10.5220/0003144102300235

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 230-235

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

slices. The annotation of the data is very exhaust-

ing. We have spent about 80 hours annotating 200

sequences, which are not enough for feature induc-

tion and supervised learning of CRFs. This difﬁculty

motivated the idea of the simulation.

A sequence generator was built to create data se-

quences, and to label them automatically, simulating

the data of the table soccer games. The core idea is to

create the ﬁrst CRFs, with the feature functions and

the parameters generated randomly. Then, the sec-

ond CRFs can be obtained from the feature induction

methods as mentioned above. The ﬁrst CRFs can thus

provide the information to estimate the second one

and the induction algorithm. This approach creates

an extra phase to explore several basic properties of

the feature induction of linear-chain CRFs. Conse-

quently, it fosters several further developments. The

highlights of this work are summarized as follows:

• We integrate a novel reduction step in the induc-

tion, which can keep the accuracy of the predic-

tion and decrease the number of feature functions,

thus making the learning more efﬁcient.

• We develop a method to train a queue of CRF

models from the data. CRF queues guarantees

a no worse prediction accuracy than the single

CRFs. It outperformed the single ones on the data

sets in all the conﬁgurations. To the best of our

knowledge, we are the ﬁrst who propose the idea

of CRF queues.

1.1 Related Works

Variable and feature selection is a well-developed re-

search area. Guyon summarized the issues and the

main approaches in the area in (Guyon and Elisse-

eff, 2003). If we put the speciﬁc CRFs problem into

a more general context, many ideas and methods can

be used. For example, feature reduction is widely em-

ployed in this area. To our knowledge, it is not yet

applied to CRFs.

We found only a few works about feature induc-

tion of CRFs. Chen et al. compared a gradient

based approach (Chen et al., 2009) to the McCal-

lum method. Both approaches use the framework

shown in Figure 1. In candidate evaluation, the gra-

dient based approach searches for the candidates that

make the objective function decrease fastest. Instead

of simply counting in the observation test, some re-

searchers integrated the boosting method (Dietterich

et al., 2004). The approaches in this direction can si-

multaneously induce features and train CRFs, which

have the more compact model, and therefore being ef-

ﬁcient in the computation.

Our implementation is based on a CRF training

algorithm - Stochastic Meta Descent (SMD) (Vish-

wanathan et al., 2006), and the feature induction

framework by McCallum. The experiment platform

was implemented according to the descriptions in the

publications. We did not use any existing source code

from the authors or the open source toolkit via Inter-

net. The main reason is that the sequential data in this

work are very different from the data in the synthetic

benchmarks. In addition, building a platform from

scratch creates more chances to ﬁnd unique and novel

ideas.

2 PRELIMINARIES

A game recorder was developed to record table soc-

cer games of human (Zhang and Hornung, 2008). The

data are collected from 14 sensors, which are mounted

on a regular game table. They measure the posi-

tion and angle of each game rod, and the position

of the game ball. The Frequency of the recorder is

about 200Hz. The sensor data were transferred to 52

Boolean variables via a discretization method. The

labeling task is to identify the skills of human.

In this work, we deﬁne the data by using a typ-

ical notation in data classiﬁcation. The sequential

data has the form (X,Y), where X is an observation

sequence (B

,...,B

) and Y is the state sequence.

Y = (y

,...,y

), where I is the length. At each state

, a corresponding B

can be observed, which is a

vector of Boolean variables, B

= (b

i,1

i,2

,...,b

i,C

where C is the number of the variables.

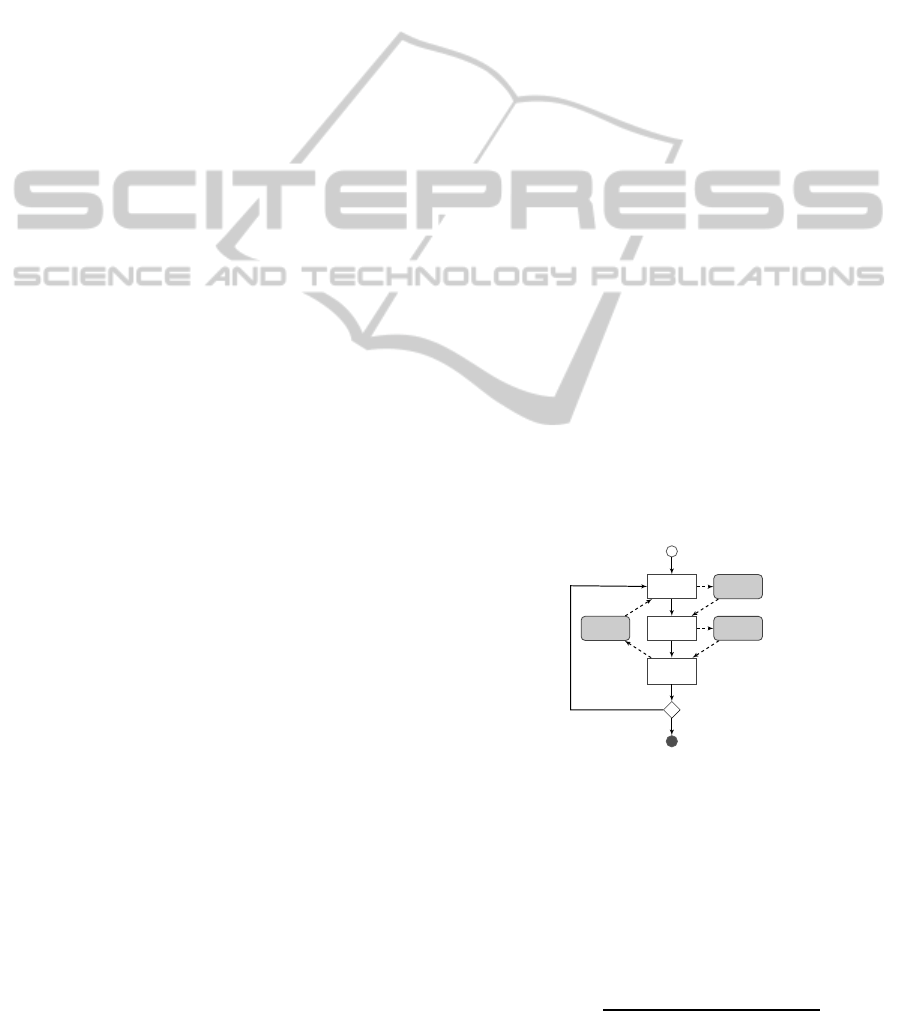
Figure 1: The Feature Induction of CRFs.

Conditional Random Fields is an undirected

graphic model in the exponential family. The clique

decomposition of CRFs supports the inference of the

distributes in an arbitrary graph structure. We focus

on linear-chain structure in this paper. In CRFs, the

probabilities of a sequence of labels Y given the ob-

servations X are deﬁned in the following equation.

p(Y|X) =

exp(

∑

i=1

Θ·F(y

i−1

,X))

Z(X)

(1)

FEATURE INDUCTION OF LINEAR-CHAIN CONDITIONAL RANDOM FIELDS - A Study based on a Simulation

231

The parameters Θ of CRFs can be estimated by

a training process, in which F is assumed to be

known. Given the training data D = (X,Y), where

X = {X

,...,X

}, Y = {Y

,...,Y

}, the train-

ing algorithm maximizes the likelihood of the CRF

model.

∗

= argmax

∑

n=1

p(Y

) (2)

Feature induction is a difﬁcult problem because

training CRFs requires considerable computational

power. In McCallum’s approach, there are mainly

three layers of the evaluations (McCallum, 2003),

shown as three rectangles in the center of Figure 1.

From top to bottom, each step to the lower layer re-

quires more computational powers of several levels of

signiﬁcance. In candidate evaluation, each candidate

is evaluated by measuring how much it can increase

the gain G( f

K+1

), given in Equation 3.

G( f

K+1

) = max

K+1

∑

n=1

K+1

) − p(Y

)) (3)

Here p

K+1

is from the CRFs that includes an extra

candidate f

K+1

. Its weight θ

K+1

can be calculated

by ﬁxing Θ so that the evaluation can be done much

faster than training the whole CRFs.

3 SIMULATION

A CRF model describes a stochastic process, which

reveals the relations among the observations and the

hidden labels. In the training process, the success of

the CRFs hints that the acquired stochastic process

matches the patterns in the data. First the training data

are avaiable, then the CRFs is trained from them. The

idea of the simulation goes the retrograde way. First

a CRFs is generated, then it can be used to compute

the hidden labels of any randomly generated observa-

tions. The following is the assumption which bridges

the simulation and the simulated process.

• The stochastic processes in the target system

can be described as a CRF model.

The simulation is shown as the upper row of the

boxes in Figure 2. There are mainly two algorithms.

A CRF model is generated by the model generator.

The Simulation provides a platform for studying a

wide range of CRFs. After we exploring on differ-

ent situations, ﬁve conﬁgurations {S

}

are carefully chosen, which are challenging for the

induction issues, being not too hard or too easy. The

conﬁgurations are designed for the comparisons of

Figure 2: Trainning of CRFs with the shared features.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

Trained Model Simulated Model

Right Sequence Probability

Wrong Sequence Probability

Prediction Accuracy

Figure 3: A comparison to

the simulated Models.

0.6

0.7

0.8

0.9

S1 S2 S3 S4 S5

Prediction Accuracy (on Sequences)

minimum

average

maximum

Figure 4: The accuracy of

the trained CRFs.

the different levels of the conjunctions and the inter-

dependencies.

The simulation was run to create the following

data: 100 data sets for each conﬁguration S

. Each

set contains a training set of 1000 sequences, and a

test set of 500 sequences.

3.1 The Trained CRFs

The experiments are based on 8 computers, each with

8 AMD cores at 2.3GHz and 32G memory. These

CPUs are driven by a grid system, on which 64 tasks

can be run in parallel. The experiments described in

this paper altogether took about 14 days in the grid

system.

In the ﬁrst experiment, we assume F is known.

Figure 2 shows the scenario. The training algo-

rithm (SMD) was run for maximum 10000 iterations

(batches) on each data set, so that the resulted CRFs

are well-trained. The trained model and the simulated

model are compared in three aspects. The results are

shown in Figure 3. We denote the correct sequence

probability as p

, and p

is the wrong probability.

The prediction accuracy is the rate of the correct se-

quences. The values in the ﬁgure are the average val-

ues over all 500 models and the data sets.

We can summarize the observations as follows:

The simulated CRFs cannot be cloned via supervised

learning. With the shared feature function, the trained

CRFs can achieve an average accuracy of about 90%.

The detailed information on the trained models

over the conﬁgurations are shown in Figure 4. We

inspect the prediction accuracy of the trained models.

By using each conﬁguration, 100 simulated models

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

232

0.4

0.6

0.8

0.05 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 0.95

0.2

0.4

Prediction Accuracy (on Sequences)

Data Distribution

Most Probable Path Probability

Figure 5: The distributions of the accuracy of the prediction

over the probabilities of the most probable path.

were generated. “Minimum” means the trained model

performed worst in the estimation, while “maximum”

is the best. The average performances of the trained

models are roughly the same over the ﬁve conﬁgura-

tions. The performance of a trained CRFs depends on

both F and Θ of the simulated model. Θ itself has

signiﬁcant impact on the performance.

The trained CRFs can not only compute the most

possible explanation for an input X, but also associate

this explanation with a probability value. In Figure

5, we show the relations between the prediction accu-

racy and the probability of the most probable paths.

The ﬁgure consists of two parts. The upper part is

about the accuracy of the prediction. The lower part

is the distributions of the data in each grid.

These distributions are interesting. If there is an

axis for the probability of the most probable path, the

training based on maximum likelihood pushes a large

number of sequences in the training set towards the

higher value direction of the axis. If the axis is divided

into two parts at the middle point, the higher part has

a higher accuracy than the lower part.

4 FEATURE INDUCTION

The induction process iterates over three steps. In

this section, we develop the forth step: feature re-

duction. A subset of features F

is to be removed

from F, where F is the set of so far induced features,

⊂ F. For each f

∈ F, a gain value G

is deﬁned

as a measurement for the reduction. We modiﬁed the

gain G( f

K+1

) in Equation 3 for the reduction. The

difference is f

K+1

/∈ F, while f

∈ F. G is calculated

in iterations before the traing of the CRFs; G

can be

calculated without any iteration after the training. In

the reduction, the features with a G

lower than a pre-

deﬁned threshold C

can be removed.

( f

) =

∑

n=1

(p(Y

) − p

)) (4)

′

= F − { f

( f

) < C

} (5)

The induction algorithm with feature reduction is

written in pseudo-code in Table 1. The reduction is

Table 1: Algorithm: Inducing Features with Reduction.

input: Training Examples (X,Y)

output: CRFs: (F, Θ)

1 F

0,I

2 for i

= 1...I

3 F

= F

−1,I

4 for i

= 1...I

5 F

= F

−1

∪

{new Features from the Observation Test}

6 Compute Θ

on F

via Equation 2

7 end

8 Reducing F

via Equation 5

9 end

10 Choose F = F

where F

yield to the best

performance on the (X,Y)

11 Compute Θ on {F

,Θ

} via Equation 2

12 return (F,Θ)

0.5

1.5

0 5 10 15 20 25 30 35 40 45 50

Average Time Spent (in seconds)

Iterations of Inducing Features

Incremental Inducing

with Feature Reduction

Figure 6: Time spent on the

training.

0.45

0.55

0.65

0.75

S1 S2 S3 S4 S5

Prediction Accuracy (on Sequences)

Incremental Inducing

with Reducing

CRF queue

Figure 7: The Evaluation.

called after several iterations of observation test, can-

didate evaluation, and CRFs training. The algorithm

stops after some iterations of the reduction steps.

In the training process, each feature function has

a weight. Intuitively, the feature reduction can reduce

the number of parameters. Consequently, it should

save the computational power required by the train-

ing. The second experiment is designed for this com-

parison. The feature induction algorithms are run in-

dependently with and without the reduction for 50 it-

erations. Figure 6 shows the results.

In the ﬁgure, the horizontal is the function calls

of the training. The vertical is average time spent on

processing 100 batches of SMD. During the induction

process, features are added to F incrementally. The

training thus requires more and more time to compute

the weights of the feature functions. The dotted curve

shows the performance of the algorithm with feature

reduction. It is serrated because the reduction step is

not called in every iteration. The reduction step can

save the computational power more than 30% in the

long run.

Although the reduction makes the induction pro-

cess faster, does it decrease the prediction accuracy

of the resulted CRFs? The third experiment is de-

signed to investigate this issue. The induction algo-

rithms with and without the reduction were run inde-

pendently over the 5 × 100 training sets. The models

which yield to the best performance on the training

set are selected for the evaluation. The results are il-

lustrated in Figure 7. Based on the average results,

FEATURE INDUCTION OF LINEAR-CHAIN CONDITIONAL RANDOM FIELDS - A Study based on a Simulation

233

the algorithm with the reduction outperformedthe one

without reduction in all the conﬁgurations.

In Figure 7, the performances of the models can

be roughly classiﬁed into two categories: {S

} the

conﬁgurations with single features, and {S

}

the conﬁgurationswith conjunctivefeatures. The con-

junctive features of the simulated models make the in-

duction tasks more difﬁcult. The feature overlapping

of the simulated models [only] slightly affects the dif-

ﬁculties of the induction in the experiments.

As illustrated in Figure 6, the algorithm with the

reduction runs faster because the number of feature

functions is lower. How many features were induced

in the experiments? In the upper part of Figure 8, we

show the results. The “13” comes from the simulated

models, which serves as a based line for the compar-

ison. The learning induced the features several times

more than the target features in the simulated mod-

els. Surprisingly, it did not cause a severe overﬁtting

problem. For the induction with the reduction, com-

pared to the conﬁgurations with conjunctive features,

more features were induced in the conﬁgurations with

a single feature.

4.1 CRF Queues

In Section 3.1, the experiments showed that along the

axis of the probabilities of the most probable paths, a

higher value has a higher accuracy. The basic idea of

CRF queues is to build a queue of CRF models, and

each model uses the higher probability part to do the

prediction. If the probability of a sequence is lower

than a threshold t, the data are passed to next model.

r(D,t) = {(X

′

)|(X

′

) ∈ D, p(Y

′′

′

) > t)}

If D(X,Y) is the training set, a ﬁlter function is de-

ﬁned as follows, whereY

′′

is the most probable expla-

nation of X

′

. We deﬁne D

′

⊂ r(D,t) as the set of the

sequences which are correctly explained. The thresh-

old t

∗

can be calculated via:

∗

∼

arg

′

|r(D,t)|

) = C

(6)

In the equation, C

is a selected accuracy higher

than the accuracy of the ﬁrst CRFs in the queue. In

order to build the queue, assume the ﬁrst CRF model

is already induced via the algorithm shown in Table

1 – we can then use t

∗

to ﬁlter the training set for

the next model in the queue. The sequences with a

probability of the most probable explanation higher

than t

∗

are removed from the training set. The rests

are used to induce the next model in the queue.

m+1

= D

− r(D

∗

) (7)

Table 2: Algorithm: Inducing CRF Queue from Data.

input: Training Examples D(X,Y)

output: Learned CRF Queue

Q((F

,Θ

),t

),m = 1...M

1 D

= D; Q

= (

0, ⊥)

2 for m=1...M do

3 Compute (F

,Θ

) on D

via table 1

4 Compute t

on D

via Equation 6

5 Q

= Q

m−1

∪ ((F

,Θ

),t

)

6 Compute D

m+1

by Applying ((F

,Θ

),t

)

on D

via Equation 7

7 end

8 return Q

100

120

Incremental Inducing

with Feature Reduction

2.5

3.5

S1 S2 S3 S4 S5

The Number of CRFs in the queue

Figure 8: feature functions

and CRFs in the queue.

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

CRFs-1 CRFs-2 CRFs-3 CRFs-4 CRFs-5

Train Set Size

Accuracy of the Model

Accuracy of the Filtered Model

Accuracy of the Queue

Figure 9: An Example of

CRF Queue.

The algorithm of inducing CRF queues is written

in pseudo-code in Table 2. In each iteration, a CRF

model is built; the threshold is computed; and the

training set is ﬁltered. The algorithm is run until no

CRFs with the required accuracy (C

) can be induced

from the ﬁltered data.

A sequence X can be explained by the queue in the

following way. X is explained by the ﬁrst model p

the queue. If p

′

|X) > t

, where t

is the threshold,

then Y

′

is the explanation of the X. Otherwise, X is

passed to the second model. If X cannot be explained

by any of the models in the queue, the model with the

highest accuracy is chosen to explain the sequence.

Figure 9 shows an example of the CRF queue.

There are 5 models altogether in the queue. The

ﬁrst column in the ﬁgure shows the training set used

for the model. In the experiment, each training set

consists of 1000 sequences. 1.0 means all of them are

used to induce CRF-1. Along the queue, fewer and

fewer data are passed to the next model. CRF-5 is

trained by less than 300 sequences.

The second column in the ﬁgure illustrates the per-

formance of each model on the training set. To our

surprise, so many models can be induced with the re-

duced training sets. Their performances on the train-

ing data can be improved by inducing a new set of the

features. The third column is the accuracy of using

the model with the threshold t

, we call it the ﬁltered

model. t

deﬁnes the higher part along the axis of the

probability of the most probable paths. CRF queues

provide a more accurate prediction because the third

column is higher than the second one. The fourth

column is the performance of the CRF queue. It is

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

234

computed by using the current acquired models. For

example, in CRF-3, the ﬁrst, second, and third mod-

els build the queue. Along the queue, the evaluations

are better and better. In CRF-1, the second column is

higher than the fourth one because of overﬁtting. The

performance of the model is better on the training set

than on the test set.

In the example, if X cannot be explained with

a probability higher than the threshold t

by all the

models in the queue, CRFs-5 should be chosen to ex-

plain X. The reason is that its second column is the

highest one over the second columns of all the mod-

els. To summarize, the third columns of the ﬁrst four

models and the second column of the ﬁfth model are

chosen to explain X. Their overall performance, the

fourth column in CRFs-5, is lower than any of these

columns because of overﬁtting. From another point of

view, the values of the chosen columns are based on

the training data; the overall estimation of the queue

is the evaluation on the test set.

The fourth experiment was designed to evalu-

ate CRF queue. The algorithm shown in Table 2

was run on all data sets. The average results over

5 conﬁgurations are shown as the third columns in

Figure 7. The CRF queue outperformed the single

model approaches for about 4% on average in all con-

ﬁgurations. We show the number of models in the

queue in the lower parts in Figure 8. The results

are averaged over the 100 sets in each conﬁgurations.

The number of models is above 3, which hints that

the queue works well in most cases. {S1, S3} has a

shorter queue because the performances of the single

model approaches in these conﬁgurations are better,

as shown in Figure 7. The CRF queue is shorter when

the single model approaches work better.

5 CONCLUSIONS

In this paper, we constructed a simulation fran-

mework to investigate the issues of inducing features

of linear-chain CRFs. The simulation helps to gain

a new phase to compare the simulated CRFs and the

induced CRFs. We used a large amount of experi-

ments to explore the properties of the learned CRFs.

Moreover, we developed a feature reduction method

that can be integrated into the induction process, and a

queue of CRF models can be constructed which yields

a better performance. CRF queues guarantees accu-

racy no worse than the single model approaches.

We did not use the open source CRF toolkit and

did not yet experiment on the benchmarks. In the fu-

ture, we will adapt our code to process the benchmark

data. The simulation framework sets a basis for in-

teresting research on CRFs in several directions. It

would be interesting to explore the bootstrap issues.

In CRF queue, we deﬁned a method to ﬁlter the train-

ing set. Another method could be to construct a deci-

sion tree to ﬁrst classify the training set, then use the

data in each class to induce CRFs.

REFERENCES

Chen, M., Chen, Y., Brent, M. R., and Tenney, A. E. (2009).

Gradient-based feature selection for conditional ran-

dom ﬁelds and its applications in computational ge-

netics. In ICTAI ’09: Proceedings of the 2009 21st

IEEE International Conference on Tools with Artiﬁ-

cial Intelligence, pages 750–757, Washington, DC,

USA. IEEE Computer Society.

Dietterich, T. G., Ashenfelter, A., and Bulatov, Y. (2004).

Training conditional random ﬁelds via gradient tree

boosting. In ICML ’04: Proceedings of the twenty-

ﬁrst international conference on Machine learning,

page 28, New York, NY, USA. ACM.

Guyon, I. and Elisseeff, A. (2003). An introduction to

variable and feature selection. J. Mach. Learn. Res.,

3:1157–1182.

Lafferty, J., McCallum, A., and Pereira, F. (2001). Con-

ditional random ﬁelds: Probabilistic models for seg-

menting and labeling sequence data. Proc. 18th Inter-

national Conf. on Machine Learning, pages 282–289.

McCallum, A. (2003). Efﬁciently inducing features of con-

ditional random ﬁelds. In UAI, pages 403–410.

Rabiner, L. R. (1990). A tutorial on hidden markov models

and selected applications in speech recognition. pages

267–296.

Vishwanathan, S. V. N., Schraudolph, N. N., Schmidt,

M. W., and Murphy, K. P. (2006). Accelerated train-

ing of conditional random ﬁelds with stochastic gra-

dient methods. In ICML ’06: Proceedings of the 23rd

international conference on Machine learning, pages

969–976, New York, NY, USA. ACM.

Zhang, D. and Hornung, A. (2008). A table soccer game

recorder. In Video Proceedings of the IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems (IROS).

FEATURE INDUCTION OF LINEAR-CHAIN CONDITIONAL RANDOM FIELDS - A Study based on a Simulation

235