MULTIOBJECTIVE OPTIMIZATION OF THE 3D TOPOLOGICAL

ACTIVE VOLUME SEGMENTATION MODEL

Jorge Novo, Manuel G. Penedo and Jos

e Santos

Computer Science Department, University of A Coru

na, Campus de Elvi

na s/n 15071, A Coru

na, Spain

Keywords:

Deformable segmentation models, Genetic algorithms, Evolutionary multiobjective optimization.

Abstract:

In this work it is proposed an evolutionary multiobjective methodology for the optimization of topological

active volumes. This is a 3D deformable model that integrates features of region-based and boundary-based

segmentation techniques. The model deformation is controlled by energy functions that must be minimized.

Most optimization algorithms need an experimental tuning of the energy parameters of the model in order to

obtain the best adjusted segmentation.

To avoid the step of the parameter tuning, we developed an evolutionary multiobjective optimization that

considers the optimization of several objectives in parallel. The proposed methodology is based on the SPEA2

algorithm, adapted to our application, to obtain the Pareto optimal individuals. The proposed method was

tested on several representative images from different domains yielding highly accurate results.

1 INTRODUCTION

The active nets model (Tsumiyama and Yamamoto,

1989) was proposed as a variant of the deformable

models (Kass et al., 1988) that integrates features

of region–based and boundary–based segmentation

techniques. To this end, active nets distinguish two

kinds of nodes: internal nodes, related to the region–

based information, and external nodes, related to the

boundary–based information. The former model the

inner topology of the objects whereas the latter ﬁt the

edges of the objects.

The Topological Active Net model and its exten-

sion to 3D, that is, the Topological Active Volume

(TAV) model (Barreira and Penedo, 2005), were de-

veloped as an extension of the original active net

model. It solves some intrinsic problems to the de-

formable models such as the initialization problem.

The model deformation is controlled by energy func-

tions in such a way that the mesh energy has a mini-

mum when the model is over the objects of the scene.

The TAV model is an active model focused on seg-

mentation tasks that makes use of a volumetric dis-

tribution of the nodes. It integrates information of

edges and regions in the adjustment process and al-

lows to obtain topological information inside the ob-

jects found. This way, the model, not only detects

surfaces as any other active contour model, but also

segments the inside of the objects. The model has a

dynamic behavior by means of topological changes

in its structure, that enables accurate adjustments and

the detection of several objects in the scene.

There is very little work in the optimization of ac-

tive models with genetic algorithms (GA), mainly in

edge or surface extraction (Ballerini, 1999; S

eguier

and Cladel, 2003a) in 2D tasks. For instance, in

(Ballerini, 1999) the author developed the “genetic

snakes”, this is, snakes that minimize their energy by

means of genetic algorithms. In (Ib

nez et al., 2009)

the authors proved the superiority of a global search

method by means of a GA in the optimization of the

Topological Active Nets model in 2D images. The

results showed that the GA is less sensitive to noise

than the usual greedy optimizations and does not de-

pend on the parameter set or the mesh size.

Regarding 3D images, the authors in (Jones and

Metaxas, 1997) used deformable contours to estimate

organ boundaries. They integrated region-based and

physics-based boundary estimation methods. Starting

from a single voxel within the interior of an object,

they made an initial estimate of the objects boundaries

using fuzzy afﬁnity, which measures the probability

of two voxels belonging to the same object, together

with clustering. In (Qiu et al., 2004) the authors used

two deformable models: a deformable surface model

(SMD) and a Deformable Elastic Template (DET).

The main drawback of these models, as the authors

indicate, is that in both models an initial shape (sur-

face or ellipsoid) is needed as well as it must be manu-

ally positioned in the data/image. The same drawback

236

Novo J., G. Penedo M. and Santos J..

MULTIOBJECTIVE OPTIMIZATION OF THE 3D TOPOLOGICAL ACTIVE VOLUME SEGMENTATION MODEL.

DOI: 10.5220/0003144302360241

In Proceedings of the 3rd International Conference on Agents and Artiﬁcial Intelligence (ICAART-2011), pages 236-241

ISBN: 978-989-8425-40-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

can be associated with adaptive deformable models,

typically with only surface modelling, which use a

reparameterization mechanism that enables the evo-

lution of surfaces in complex geometries. In (McIner-

ney and Terzopoulos, 1999) it is used a model of this

type with complex anatomic structures from medical

images.

The author in (Bro-Nielsen, 1994) used 3D “ac-

tive cubes” to segment medical images, where the au-

tomatic net division was a key issue. Since the greedy

energy-minimization algorithm proposed was sensi-

tive to noise, an improved greedy algorithm inspired

by a simulated annealing procedure was also incorpo-

rated. In (Novo et al., 2007) the authors proposed a

GA with new deﬁned operators for the segmentation

process using TAV structures. The genetic approach

overcame some drawbacks, basically in images with

different types of noise, with regard to the work pro-

posed in (Barreira and Penedo, 2005). The main prob-

lem of the TAV model, as in other deformable models,

is that it is necessary an experimental tuning of the

parameters that weights the different energy compo-

nents that are used for the optimization of the model.

These weights are usually very dependent on the kind

of image to segment.

Multiobjective Optimization Algorithms (MOAs)

give a solution to this problem by considering the

optimization of several objectives in parallel. The

MOAs usually work with conﬂicting objectives try-

ing to identify a set of optimal trade-off solutions or

nondominated solutions which is called the Pareto

Set. Multiobjective Optimization Evolutionary Al-

gorithms (MOEAs) (Deb, 2001; Jaimes and Coello,

2009), use the principles of evolutionary computing

to the search of the Pareto Set. We used in this work

one of the best-established algorithms of this type,

SPEA2 algorithm (Zitzler et al., 2002). We tested the

advantages that add the use of the MOEA method-

ology in the optimization of the active volume de-

formable models. There is practically no work using

MOEAs applied to deformable models. In the work

eguier and Cladel, 2003b), a multiobjective opti-

mization of different energy components was devel-

oped to the optimization of snakes in an audio-visual

speech recognition task. The authors optimized two

snakes to ﬁt the external and interior lips contours, us-

ing only a small limited number of contour points for

each snake. After the evaluation of the snakes energy

components, the chromosomes were ranked and, this

way, the Pareto optimal solutions were searched. Ac-

cording to the authors, the multiobjective optimiza-

tion required less iterations than an usual genetic op-

timization.

2 TOPOLOGICAL ACTIVE

VOLUMES. DEFINITION OF

OBJECTIVES

A Topological Active Volume (TAV) is a discrete im-

plementation of an elastic n−dimensional mesh with

interrelated nodes (Barreira and Penedo, 2005). The

model has two kinds of nodes: internal and exter-

nal, which represents different object features: the ex-

ternal nodes ﬁt the edges whereas the internal nodes

model their internal topology.

As in other deformable models, the state of the

model is governed by an energy function, composed

of an internal and an external energy term. The in-

ternal energy controls the shape and the structure of

the net whereas the external energy represents the ex-

ternal forces which govern the adjustment process.

These energies are composed of several objectives

and in all the cases the aim is their minimization.

Internal Energy Objectives. The internal energy de-

pends on ﬁrst and second order derivatives which con-

trol the contraction and bending of the mesh, respec-

tively:

int

(v(r, s,t)) = α(|v

(r, s,t)|

+ |v

(r, s,t)|

+ |v

(r, s,t)|

) +

β(|v

(r, s,t)|

+ |v

(r, s,t)|

+ |v

(r, s,t)|

2γ(|v

(r, s,t)|

+ |v

(r, s,t)|

+ |v

(r, s,t)|

)

(1)

where the subscripts represents partial derivatives and

α, β and γ are coefﬁcients controlling the ﬁrst and

second order smoothness of the net.

External Energy Objectives. The external energy

represents the features of the scene that guide the ad-

justment process:

ext

(v(r, s,t)) = ω f [I(v(r,s,t))] +

ℵ(r,s,t)

∑

n∈ℵ(r,s,t)

||v(r,s,t)−v(n)||

f [I(v(n))]

(2)

where ω and ρ are weights, I(v(r, s,t)) is the in-

tensity value of the original image in the position

v(r, s,t), ℵ(r,s,t) is the neighborhood of the node

(r, s,t) and f is a function of the image intensity,

which is different for both types of nodes. If the ob-

jects to detect are bright and the background is dark,

the energy of an internal node will be minimum when

it is on a position with a high grey level. Also, the

energy of an external node will be minimum when it

is on a discontinuity and on a dark point outside the

object. So, the function f is deﬁned as:

f [I(v(r,s,t))] =











(v(r, s,t)) + τIOD

(v(r, s,t)) internal nodes

(v(r, s,t)) + τIOD

(v(r, s,t))

+ ξ(G

max

− G(v(r, s,t)))

+ δGD(v(r, s,t)) external nodes

(3)

where τ, ξ and δ are weights, G

max

and G(v(r,s,t))

are the maximum gradient of the image and the gradi-

ent of the input image in node position v(r,s,t), IO is

a term we called “In-Out” and IOD a term called “dis-

tance In-Out”, and GD(v(r,s,t)) is a gradient distance

MULTIOBJECTIVE OPTIMIZATION OF THE 3D TOPOLOGICAL ACTIVE VOLUME SEGMENTATION MODEL

237

term. The IO terms minimize the energy of those indi-

viduals with the external nodes in background inten-

sity values and the internal nodes in object intensity

values meanwhile the terms IOD act as a gradient:

for the internal nodes (IOD

) its value minimizes to-

wards brighter values of the image, whereas for the

external nodes its value (IOD

) is minimized towards

low values (the background).

The greedy (Barreira and Penedo, 2005) and the

genetic algorithm (GA) (Ib

nez et al., 2009) aim is

the optimization of a global objective deﬁned as the

sum of the individual objectives weighted with the ex-

posed parameters: α, β, γ, ω, ρ, ξ, δ and τ. (Novo

et al., 2007) includes the deﬁnition of the genetic op-

erators used with a GA: arithmetic crossover, muta-

tion of a node, mutation of a group of neighboring

nodes, shift of a mesh and spread of a mesh. In the

case of the evolutionary Multiobjective Optimization

(MO), most of the segmentations will use the follow-

ing energy terms as independent objectives: the β en-

ergy component as a term that provides smoothness,

and a summed of IOD

(only internal nodes) and GD.

Thus, we merged both compatible properties as only

one objective.

3 ADAPTED SPEA2 ALGORITHM

SPEA2 (Zitzler et al., 2002) is an improved version of

the Strength Pareto Evolutionary Algorithm (SPEA).

The new version incorporates a ﬁne-grained ﬁtness

assignment strategy and a density estimation tech-

nique. In this section, we describe these two key as-

pects and our own adaptations.

The algorithm considers, in each generation t, a

regular population P

of size N and an archive P

(ex-

ternal set). This archive contains the nondominated

solutions and possibly some dominated solutions if

the number of nondominated solutions is less than its

size. The size of the archive (N) is ﬁxed and initially

the archive is empty (P

0).

The ﬁtness assignment takes into account domi-

nations between individuals and incorporates density

information into its calculation. First, a raw ﬁtness

R(i) is calculated based on the number of individuals

that dominates an individual i:

R(i) =

∑

j∈P

, ji

S( j) (4)

where S( j) represents the “strength” of individ-

ual j, that is, the number of individuals it dominates.

This raw ﬁtness of an individual i is calculated using

the dominations in both the archive and population

set. This way, the individuals of the Pareto Set have a

value R = 0, whereas a high value of R means that the

individual is dominated by many other individuals.

If several nondominated individuals have the same

raw ﬁtness, a density estimation is incorporated to dis-

criminate between them. Thereafter, a density D(i) is

then calculated:

D(i) =

+ 2

(5)

The term σ

represents the distance from i to its

k − th nearest neighbor, being k =

N + N, taking

into account any member of the archive set and pop-

ulation. Finally, adding both terms, the individual ﬁt-

ness is calculated as:

F(i) = R(i) + D(i) (6)

The k−distance deﬁned in SPEA2 uses the entire

population to calculate the distances (Eq. 5). In-

stead, we consider only the nondominated ones, be-

cause these are the individuals mainly contained in the

archive, which is used for producing the new individ-

uals in the new population. We gain speed because we

calculate only a small portion of the distances com-

pared to the original algorithm.

Additionally, instead of the original k−distance,

we calculate an average k−distance as follows. First,

after sorting the list of distances for each individual

in increasing order, we consider only a window of

the list represented by the 8th part of the closest in-

dividuals. Finally, the distance σ

is an average over

the k-distances that represent the 25%, 50%, 75% and

100% positions on that window. That way, the dis-

tance σ

gives a more accurate view of the level of

neighborhood of an individual, and with emphasis in

the immediate neighborhood.

The next step in the algorithm is the environmen-

tal selection which deﬁnes how the archive maintains

the Pareto Front. In each generation we get a new

set of nondominated individuals in P

and P

, and the

archive must be updated taking into account the ﬁxed

size restriction N. The archive update operation has

to consider all possible situations: If the total size of

the nondominated set is equal to (

N) all the new non-

dominated individuals are copied to the archive. If the

archive is large, not only the new nondominated indi-

viduals are copied to it, but also the best N − |P

t+1

dominated individuals. If it is small, the worst non-

dominated individuals in terms of ﬁtness are removed

until |P

t+1

| = N, using a truncation operation.

The termination condition is checked next. If it is

satisﬁed, the output is the set of decision vectors rep-

resented by the nondominated individuals in P

t+1

. If

the stopping condition is not met, then mating selec-

tion is performed. We used tournament selection with

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

238

replacement on P

t+1

to ﬁll the mating pool. Then, re-

combination and mutation operators are applied to the

mating pool setting P

t+1

to the resulting population.

Concretely, we applied an arithmetical crossover

and mutation operators, as well as other ad hoc oper-

ators previously developed for the optimization of the

active model with a GA as proposed in (Novo et al.,

2007). Figure 1 shows an example of the arithmetical

crossover between two parents to produce two new

individuals (TAVs) with average topologies between

the two selected parents. Moreover, we incorporated

elitism, deﬁned over each objective. This means that

we maintain in the next generation (in the external

archive) the best individuals that minimize each one

of the objectives. By doing this, we maintain the in-

dividuals of the extremes of the Pareto Front in the

next generation. We used this option with the objec-

tives that the user can consider as the most important

to minimize, as can be the case of the IOD

/GD that

optimizes the external contour segmentation.

Figure 1: Arithmetical crossover operator. 1

row, selected

parents. 2

row, offspring after the crossover.

4 RESULTS

This section presents some representative results ob-

tained with the methodology developed. To test

the method, we selected some representative images

taken from different domains: artiﬁcial images, that

were designed to show its capabilities, and CT im-

ages, taken from the medical domain to test the pro-

cess in a real one. Every image is composed by a

given number of slices, normally between 90 and 130,

that compose the 3D image. This set is the input to the

procedures which calculate the different energy terms.

In the multiobjective processes we used an archive

size of 100 individuals and a population size of 2000

individuals. The tournament size was a 3% of the

archive size. We also used elitism over the IOD

/GD

objective to keep in the population the individual with

the best adjustment to the object contour.

Table 1: TAV parameter sets of the GA 2nd phase in the

segmentation processes of the examples.

Figure α β γ ω ρ ξ δ τ

3 (b) 2.0 1.5 0.1 1.0 4.5 5.0 10.0 1.0

3 (c) 2.0 1.5 0.1 10.0 4.5 5.0 10.0 10.0

Firstly, we tested the method with artiﬁcial im-

ages. In Figure 2 the results obtained with different

images are shown. The 1

row shows the original im-

age to be segmented or a composing slice (ﬁrst col-

umn), the 3

row shows an intermediate individual

taken from the Pareto Front and 2

and 4

rows rep-

resent the extremes of the Pareto Front for each ob-

jective β and IOD

/GD, respectively. These meshes

shown in Figure 2, 2

row, correspond to the best

segmentations regarding the β objective (smoothness)

with the optimum values (best possible smoothness)

because the procedure creates the initial random TAVs

with cubic and regular distributions of the nodes.

Nevertheless, although the best individual regarding

such objective is present from the beginning, it acts

as a point that delimits and forces the progression of

the trade-offs nondominated individuals of the Pareto

Front. As we can see in the results, the individual that

optimizes the IOD

/GD objective provided the best

adjustment to the contour that the process could ob-

tain. In all the trade-offs obtained from the middle

of the Pareto Front we can point out the compromise

obtained between the smoothness and the contour de-

tection searched in the extremes of the Pareto Front.

Figure 2: Results obtained in the segmentation of artiﬁcial

images. 1

row, original image. 2

row, best individual by

β objective. 3

row, intermediate nondominated individual.

row, best individual by IOD

/GD objective.

We also tested the methodology developed with

artiﬁcial images specially designed with a higher level

MULTIOBJECTIVE OPTIMIZATION OF THE 3D TOPOLOGICAL ACTIVE VOLUME SEGMENTATION MODEL

239

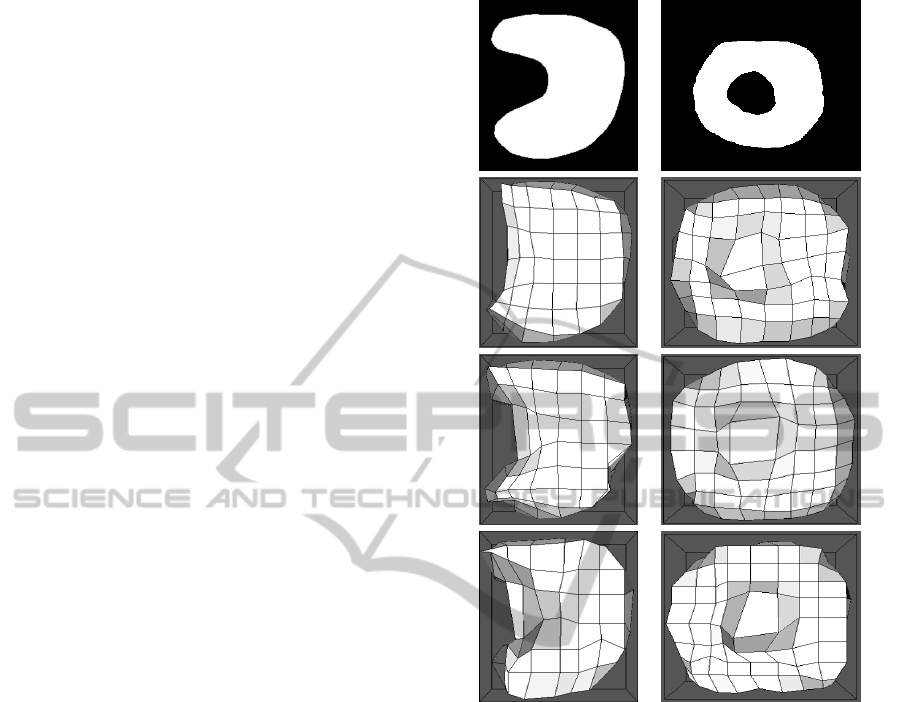
of complexity, in particular containing objects with

deep concavities and holes. In Figure 3, two seg-

mentation examples are shown. These 3D images are

composed by the given slices repeated over 90 times.

In this case we include the results obtained with

a genetic algorithm (GA) to show the main problem

of a single-objective optimization procedure. As ex-

plained in (Novo et al., 2007) two evolutionary phases

are needed: a ﬁrst evolutionary stage to obtain indi-

viduals (TAVs) that detect and cover the object and a

second stage to improve the adjustment progressively.

The parameters used in the ﬁrst phase of the GA pro-

cesses were always the same. The values employed

were: α = 0.00001, β = 0.00001, γ = 0.0, ω = 1.0,

ρ = 1.0, ξ = 0.0, δ = 10.0, τ = 0.0. For the sec-

ond phase of the GA processes we depict in Table 1

the tuned parameters that were used. The GA used

a population size of 2,000 individuals and a tourna-

ment size of 3% of the population. The GA method

using a typical parameter conﬁguration (Table 1, ﬁrst

row, parameters tuned for different kinds of no com-

plex images) cannot obtain a correct detection of the

holes and concavities. This is shown, for example,

in Figure 3, 2

row, where some internal nodes fall

in the hole, which is not correctly delimited. In this

case it is necessary to perform a speciﬁc tuning of the

parameters (Table 1, second row) to detect them (forc-

ing the weight parameters ω and τ to high values), as

shown in Figure 3, 3

row. However, the multiobjec-

tive method, due to the IOD

/GD objective, preserved

individuals of the Pareto Front that perform a correct

detection in these complex areas. This can be seen

in Figure 3, 4

row, representing the best individual

from the Pareto Front considering the mentioned ob-

jective, IOD

/GD.

Other kind of images that were used to test the

methodology were CT images taken from the medical

domain. Thus, we can analyze the segmentation re-

sults in a real domain. In Figure 4 three representative

examples are shown presenting a high level of com-

plexity or a signiﬁcant level of noise surrounding the

surface of the objects. The proposed method provided

a correct segmentation of the objects in these difﬁ-

cult situations. The nondominated individuals corre-

spond to those which minimize the IOD

/GD objec-

tive. Figure 4, 1

row, corresponds to a foot. The in-

put images are noisy CT images of different slices of

such foot. Due to the complex surface of this object,

we performed a previous stage in this segmentation to

obtain a population of individuals that ﬁrstly identify

the boundary of the foot. This follows the process of

2 stages or evolutionary phases as proposed in (Novo

et al., 2007) with a GA. In a ﬁrst stage, or localization

and boundary detection stage, we used IO and GD as

Figure 3: Results obtained in the segmentation of complex

objects. 1

row, slice of the original image. 2

row, ﬁ-

nal results with the GA method and typical parameters. 3

row, ﬁnal results with the GA method and speciﬁc param-

eters. 4

row, nondominated individuals at the end of the

evolutionary process.

objectives, and then a second stage to reﬁne the results

using the mentioned objectives of β and IOD

/GD.

The second example corresponds to a vertebra

from CT slices. The nondominated selected individ-

ual delimits correctly the internal hole, performing a

reasonable boundary detection. The third one corre-

sponds to the segmentation of a humerus. In this case,

the CT images are very noisy, with an additional ex-

ternal contour (the ﬂesh of the leg) that the optimiza-

tion method must avoid. Moreover, the boundary of

the bone is fuzzy. This can be seen in the ﬁnal non-

dominated and selected individual, where a group of

external nodes stretch the mesh in a extreme to de-

limit the brighter area of the bone boundary, as the

CT images of such extreme indicate.

ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence

240

Figure 4: Results obtained in the segmentation with real im-

ages. First column, CT slice or 3D reconstruction of the ob-

ject to segment. Second column, example of nondominated

individual at the end of the evolutionary process.

5 CONCLUSIONS

In this paper, we presented a new approach to the en-

ergy minimization task in the Topological Active Vol-

ume model for image segmentation. The proposed

multiobjective method is inspired in the SPEA2 algo-

rithm, being adapted to our speciﬁc application. We

incorporated the classic genetic operators as well as

new ad-hoc ones, including some modiﬁcations as a

new density estimation technique used to deﬁne the

ﬁtness of an individual.

The main problem of previous methods for the

optimization task, as a greedy algorithm or a GA,

is the need of a experimental tuning of the parame-

ters that weight the energy terms in order to obtain

correct segmentations in each kind of images. This

drawback is directly solved with the multiobjective

method. Moreover, our MO approach works with two

objectives that summarize all the characteristics we

need for a segmentation process (smoothness, bound-

ary adjustment, detection of irregularities), so a single

evolutionary phase was required in most of the cases.

Additionally, the designer can choose from the ﬁnal

Pareto Front a trade-off segmentation or one which

minimizes a particular required objective.

ACKNOWLEDGEMENTS

This paper has been funded by the Ministry of Science

and Innovation of Spain (project TIN2007-64330)

and by the Instituto de Salud Carlos III (grant contract

PI08/90420) using FEDER funds.

REFERENCES

Ballerini, L. (1999). Medical image segmentation using ge-

netic snakes. In Proceedings of SPIE: Application and

Science of Neural Networks, Fuzzy Systems, and Evo-

lutionary Computation II, volume 3812, pages 13–23.

Barreira, N. and Penedo, M. G. (2005). Topological Ac-

tive Volumes. EURASIP Journal on Applied Signal

Processing, 13(1):1937–1947.

Bro-Nielsen, M. (1994). Active nets and cubes. Technical

Report 13, IMM, Technical University of Denmark.

Deb, K. (2001). Multi-objective optimization using evolu-

tionary algorithms. Wiley, Chichester, UK.

nez, O., Barreira, N., Santos, J., and Penedo, M. (2009).

Genetic approaches for topological active nets opti-

mization. Pattern Recognition, 42:907–917.

Jaimes, A. and Coello, C. (2009). Multi-objective evolu-

tionary algorithms: A review of the state-of-the-art

and some of their applications in chemical engineer-

ing. In World Scientiﬁc, pages 61–90.

Jones, T. N. and Metaxas, D. N. (1997). Automated 3D seg-

mentation using deformable models and fuzzy afﬁnity.

15th International Conference on Information Pro-

cessing in Medical Imaging - LNCS, 1230:113–126.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(2):321–323.

McInerney, T. and Terzopoulos, D. (1999). Topology adap-

tive deformable surfaces for medical image volume

segmentation. IEEE Transactions on Medical Imag-

ing, 18(10):840–850.

Novo, J., Barreira, N., Santos, J., and Penedo, M. G. (2007).

Topological active volumes optimization with genetic

approaches. XII Conference of the Spanish Associa-

tion for the Artiﬁcial Intelligence, 2:41–50.

Qiu, B., Clarysse, P., Montagnat, J., Janier, M., and Vray, D.

(2004). Comparison of 3D deformable models for in

vivo measurements of mouse embryo from 3D ultra-

sound images. In Ultrasonics Symposium, 2004 IEEE,

Vol. 1, pages 748–751.

eguier, R. and Cladel, N. (2003a). Genetic snakes: Appli-

cation on lipreading. In International Conference on

Artiﬁcial Neural Networks and Genetic Algorithms.

eguier, R. and Cladel, N. (2003b). Multiobjectives genetic

snakes: Application on audio-visual speech recogni-

tion. In 4th EURASIP Conference, pages 625–630.

Tsumiyama, K. and Yamamoto, K. (1989). Active net: Ac-

tive net model for region extraction. IPSJ SIG notes,

89(96):1–8.

Zitzler, E., Laumanns, M., and Thiele, L. (2002). SPEA2:

Improving the strength pareto evolutionary algorithm.

In EUROGEN 2001, Evolutionary Methods for De-

sign, Optimisation, and Control, pages 95–100.

MULTIOBJECTIVE OPTIMIZATION OF THE 3D TOPOLOGICAL ACTIVE VOLUME SEGMENTATION MODEL

241