UNSUPERVISED 3D SEGMENTATION OF HIPPOCAMPUS

IN BRAIN MR IMAGES

Sandeep S. Kaushik and Jayanthi Sivaswamy

Center for Visual Information Technology, IIIT-Hyderabad, Hyderabad, India

Keywords:

Hippocampus, MRI segmentation, Water ﬂow, Deep brain structure, Surface evolution, Region growing, 3D

segmentation, Hippocampal volumetry.

Abstract:

The most widely followed procedure for diagnosis and prognosis of dementia is structural neuroimaging of

hippocampus by means of MR. Hippocampus segmentation is of wide interest as it enables quantitative as-

sessment of the structure. In this paper, we propose an algorithm for hippocampus segmentation that is un-

supervised and image driven. It is based on a hybrid approach which combines a coarse segmentation and

surface evolution. A coarse solution is derived using region growing which is further reﬁned using a modiﬁed

version of the physics based water ﬂow model (Liu and Nixon, 2007). The proposed method has been tested

on a publicly available dataset. The performance of this method is assessed using Dice coefﬁcient against the

ground truth provided for 25 volume images. It is consistent across volumes and the average Dice values are

comparable to a multi-atlas based method reported on a subset of the same dataset.

1 INTRODUCTION

Dementia is a clinical syndrome that affects memory

and cognitive ability of a person. It is known to be

caused due to traumatic brain injury, neurodegenera-

tive diseases, bacterial infections, prolonged epilep-

tic seizures, and so on. Some common types of de-

mentia are mild cognitive impairment (MCI) or incip-

ient dementia, Alzheimer disease (AD) or dementia of

the Alzheimer type (DAT), dementia with Lewy bod-

ies (DLB) and fronto-temporal dementia (FTD). De-

mentia is usually diagnosed based on clinical obser-

vations, presence of characteristic neurological and

neuropsychological features. Onset of dementia is

difﬁcult to diagnose with these methods. Therefore,

along with clinical diagnosis, structural neuroimag-

ing is used to enable early diagnosis so that it can

be treated at the onset. Apart from diagnosis, struc-

tural neuroimaging helps to distinguish between dif-

ferent types of dementia, to differentiate between nor-

mal aging and dementia and in differential diagnosis.

Some of the methods to assess change in brain vol-

ume by means of structural neuroimagingare volume-

try, voxel based morphometry(VBM), cortical pattern

matching and brain boundary shift integral measure-

ments. Hippocampus is the structure responsible for

long term memory in the brain and its atrophy is an

early and speciﬁc marker of dementia. The severity

of hippocampal atrophy is directly related to progress

of the underlying disease and hence reﬂects the extent

of cognitive impairment. Although atrophy rates have

been observed to be larger in entorhinal cortex than

in hippocampus, difﬁculty in unambiguously deﬁning

this structure makes its measurement highly variable.

Thus, hippocampus is the region of interest in differ-

ential diagnosis of AD and mild cognitive impairment

(MCI).

Manual labelling by experts is considered as gold

standard of hippocampal segmentation. But this is

laborious, time consuming, prone to inconsistency

and inter-expert labelling variability. Advanced im-

age analysis techniques have been used to minimise

these problems by developing semi-automatic hip-

pocampal segmentation methods or further, by ob-

taining reliable initialisation, fully automatic segmen-

tation methods. From medical imaging viewpoint,

research in segmentation of deep brain structures in

general and hippocampus in particular is motivated

by various factors like i) development of computer

aided diagnosis solution by methods. The attraction

here is the potential for high precision and consis-

tency over manual segmentation which in turn offers

reliable volumetry (Bernasconi et al., 2003); ii) study

of the characteristic pattern of a particular disease or

normal aging (Chupin et al., 2008); iii) development

of generalised segmentation algorithm applicable to

182

S. Kaushik S. and Sivaswamy J..

UNSUPERVISED 3D SEGMENTATION OF HIPPOCAMPUS IN BRAIN MR IMAGES.

DOI: 10.5220/0003145401820187

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 182-187

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

various structures (Morra et al., 2008); iv) accelera-

tion of drug trials and population study of diseases.

In general, the hippocampus, with weak edges and in-

homogeneity, acts as a good test case for a neuroseg-

mentation algorithm in both 2D and 3D (Morra et al.,

2010). Given the focus of this paper on hippocampus

segmentation, next section reviews the existing meth-

ods for the same in some detail.

1.1 Related Work

The existing methods can be classiﬁed broadly based

on the approach taken to include the domain knowl-

edge as follows: i) atlas and cohort atlas based, ii)

pattern classiﬁcation and machine learning methods

based and iii) deformable models or template based.

Segmentation via registration to a brain atlas is

class of methods followed in (Akhondi-Asl et al.,

2010; Ltjnen et al., 2010). In these methods, a neu-

roanatomic atlas is registered, i.e., spatially aligned

with the given subject image to delineate the bound-

ary of the region of interest. The registration is carried

out after geometric transformation to correct align-

ment and enhancement to correct intensity variations.

Atlas-based approaches have the advantage that ad-

vances in registration techniques can be exploited.

Thus, most of the available standard registration al-

gorithms and packages can be used for segmentation.

Standard atlases available are Harvard whole brain

atlas and MNI-Talairach atlas. They contain the la-

belled structures of the whole brain and hence can be

used to segment any structure without prior knowl-

edge about the structure. However, if the subject im-

age varies largely from the atlas in terms of age of the

subject or physical dimensions of the voxels, segmen-

tation performance suffers. To overcome this issue, a

cohort atlas is built. In cohort atlas, experts manually

segment the structure of interest on one or more sub-

ject images selected from a set of reference images.

Each or combination of these labelled data (image)

can be used as an atlas. The disadvantage of using

cohort atlas is the requirement of an expert and one or

more labelled data. Both of these methods have the

common issue of inability to handle variation in data

over larger sets. Hence, atlases are more suitable for

initialisation than for complete segmentation.

An alternative way to use domain knowledge is

with pattern classiﬁcation and machine learning tech-

niques. Statistical and anatomical prior knowledge

are learnt and used to localise and segment hippocam-

pus. Appearance based features are used to build a

context model in (Morra et al., 2010), while segmen-

tation is posed as an expectation maximisation prob-

lem in (Sabuncu et al., 2009). Prior information from

an atlas and segmentation via likelihood has been

adopted in (Akselrod-Ballin et al., 2007). Most of the

techniques depend upon the shape of hippocampus

varying within a given margin. Furthermore, since

these techniques are largely supervised, the choice of

features and modelling of the problem is critical.

Template and deformable models help use domain

knowledge in a more ﬂexible way. These methods are

derived by using prior anatomical knowledge. The

structure to be segmented is modelled and parame-

terised using shape knowledge and then deformed to

segment the structure. Minimising an energy function

via iterated conditional modes (ICM), initialised by

prior information from probabilistic atlas is described

in (Chupin et al., 2008). Although these methods have

been observed to perform well, their design and im-

plementation are very complex. Shape encoding for

segmentation has to consider all possible variations of

shape of the structure. This requires a large amount

of supervision to train the model. In some of these

methods, anatomical information derived depends on

landmark detection.

In general, while prior knowledge about brain

structures can aid the segmentation problem, there are

some costs involved in acquiring this knowledge and

obtaining a good and consistent segmentation perfor-

mance: i) adequate amount of labelled data for train-

ing, ii) age, race and disease-speciﬁc matched infor-

mation. An alternative is to use an unsupervised, hy-

brid approach. A combination of region growing and

deformable model or curve evolution is one such op-

tion. Region growing is a relatively fast algorithm

which can extract all parts of the region like curves

and narrow parts. In most of the imaging modali-

ties like optical, CT and MRI, with appropriate fea-

tures used for determining homogeneity criteria, re-

gion growing proves to be one of the simplest meth-

ods of segmentation. However, this alone does not re-

sult in an exact boundary as region growing is vulner-

able especially to weak edges and non-homogeneous

regions. The second curve evolution stage is em-

ployed to address this problem. The resulting surface

is taken as input to surface evolution. This is more ac-

curate than the conventional simple geometric surface

initialisation and much faster than manual surface ini-

tialisation. Surface evolution merely needs to adjust

the surface to exact boundaries which results in quick

convergence. An image foresting transform (IFT) for

coarse segmentation together with an active surface

solution has been proposed for liver segmentation in

CT (Pohle et al., 2003).

In this paper, a non-parametric, hybrid method

is proposed for hippocampus segmentation which

utilises only local image information. The method

UNSUPERVISED 3D SEGMENTATION OF HIPPOCAMPUS IN BRAIN MR IMAGES

183

follows the coarse segmentation and surface evolution

framework with the key differences being: the surface

is not parameterised and is evolved using a physics

based water ﬂow model (Liu and Nixon, 2007). The

water ﬂow model has been applied to 2D image seg-

mentation of synthetic images. It has been demon-

strated (but not rigorously assessed) on some 2D real

cases such as grey-white matter interface, femur from

MRI, carotid artery in MR angiogram and retinal ves-

sels; and 3D lateral ventricles. Most of these struc-

tures are homogeneous with well deﬁned boundaries.

In this paper, it is demonstrated how the water ﬂow

model can be adapted to a relatively inhomogeneous,

partially weak edged hippocampus. It is demon-

strated that, in spite of its simplicity, our hybrid algo-

rithm yields results comparable to a recently reported

method. The following section describes this method

in detail.

2 HYBRID SEGMENTATION

The water ﬂow model directs the progress of a water

front based on local image properties derived from re-

gion and edge based forces. In this paper, this model

is chosen because of the following features: i) it is a

physics based model which does not depend on image

topology and ii) it makes use of both gradient forces

and region based forces which is attractive given the

weak edged boundary of the hippocampus.

Since the water ﬂow algorithm acts on a water

front, one of the simplest methods to obtain a front

is by coarse segmentation via region growing. The

coarse segmentation stage works on intensity features

which are sensitive to intensity variation due to a bias

ﬁeld that can be present. In order to address this prob-

lem, the image volume is pre-processed for bias ﬁeld

correction. A modiﬁed fuzzy C-means algorithm pro-

posed in (Ahmed et al., 2002) is used for this pur-

pose. Here, the intensity inhomogeneity is estimated

using fuzzy logic and used to correct the slowly vary-

ing shading artefact over the image.

2.1 Coarse Segmentation

This stage begins with few seeds initialised by the

user. The protocol of choosing multiple seeds, in-

stead of one, is used so that longitudinal extremes

of hippocampus can be approximated and an initial

modelling of intensity variation can be obtained. In

the process of region growing, these seeds are used

to check for homogeneity in their immediate neigh-

bourhood and decide whether or not to include those

voxels into the region. The parameters used in ho-

mogeneity veriﬁcation are: deviation of a candidate’s

voxel value from the mean voxel value of the region

and the gradient magnitude at the candidate voxel’s

location.

2.2 Fine Segmentation

The original water ﬂow algorithm (Liu and Nixon,

2007) computes a resultant force on a voxel due to

its neighbouring voxels and decides the ﬂow action.

Three types of image forces, namely, ﬁeld, potential

and statistical forces aid or oppose the ﬂow, based on

their direction with respect to the resultant ﬁeld force.

The Field force experienced by a voxel at position

due to its neighbourhood W is given by the force

ﬁeld transformation (Hurley et al., 2005) as

) =

∑

j∈W, j6=i

L(r

)

− r

)

− r

(1)

The elements of L matrix are set to −1 when a

voxel is ﬁlled with water (it is inside the region) and

set to the gradient magnitude (edge strength) other-

wise. This results in a force which is always directed

away from the region. In a cross-sectional area A (set

to unity), the ﬂow velocity gained by a voxel is

v =

)

(2)

where R is the ﬂow resistance given by

R = e

kE(r

)

(3)

where E(r

) is the edge strength (magnitude of the

gradient) at location r

and k is the resistance control-

ling factor. Higher values of k leads to higher sensi-

tivity to edges.

In addition to the static ﬁeld force F

), image

forces such as potential force, statistical force con-

tribute to the element ﬂow. The potential force is cal-

culated based on the gradient of the edge map E. This

force is largely concentrated around the edges in the

image and hence acts as a barrier to the water ﬂow.

In the known direction of ﬂow i, given a target posi-

tion r

, the potential force experienced by the ﬂowing

element is given by

p,i

= ∇E(r

) (4)

Water ﬂow model also uses a region based statistical

force based on the Mumford-Shah functional. It re-

ﬂects the change in internal and external intensities of

a closed region and its surroundings. When the target

voxel intensity deviates largely from the equilibrium,

this force turns negative and hence checks the ﬂow.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

184

Statistical force due to a target voxel at position r

given by

s,i

ext

+ 1

(I(r

) − µ

ext

)

−

int

+ 1

(I(r

) − µ

int

)

(5)

where I(r

) is the intensity value at voxel position r

n is the number of voxels and µ is the mean of inten-

sity of the internal and external regions denoted by the

subscripts int and ext respectively. To maintain a bal-

ance in the simultaneous contribution of these forces

in the element ﬂow, they are added by a convex equa-

tion as

= αF

p,i

+ (1− α)F

s,i

(6)

In the original water ﬂow algorithm, the ﬂow of an in-

dividual waterfront voxel is not constrained explicitly

by other voxels in the front. However, its movement

should be dependent on the mobility of its surround-

ing voxels on the surface and the tension between

these voxels. Hence, a new tensile force component is

introduced which has the effect of opposing the ﬂow.

This force controls the stretching of the surface and

ensures a continuous surface without holes. The ten-

sile force experienced by a voxel at r

is calculated

using the umbrella operator approximation of Lapla-

cian given by (McInerney and Terzopoulos, 1999) as

t,i

∑

j∈N

− r

) (7)

where r

is the position of the j

surface voxel within

N neighbourhood of r

and n is the total number of

voxels in that neighbourhood.

The work done by a voxel under the inﬂuence of

all the forces combined is given by

J =

m|v

+ (F

− ηF

t,i

)S (8)

where m is mass of the element analogous to inten-

sity of the voxel and S is the preset displacement. If

work done is positive, the element moves in the direc-

tion of the resultant force for a predetermined (ﬁxed)

distance. η controls the inﬂuence of the tensile force

experienced by the surface.

3 EXPERIMENTS AND RESULTS

User initialised seed points (minimum 1 per slice)

are collected along the length of hippocampus in the

coronal view of a brain MR volume image. Based

on the extreme points, with reasonable margin on all

sides, a sub volume is extracted for faster processing.

To make sure the surface evolves properly to match

both these shapes, two sets of parameters of surface

evolution - α, η and S are used, one to suit head re-

gion and one to suit the body-tail region.

The proposed method is tested on a publicly avail-

able brain MR dataset (Jafari-Khouzani, 2010). It

consists of 25 volumes of training data with as-

sociated ground truth and 25 volumes of testing

data without any ground truth. The ﬁrst (train-

ing) set has been chosen as the test data. This

set consists of 15 volumes of T1-weighted MR im-

age data of each slice 256x256 pixels with voxel

size 0.781x0.781x2.00mm

and 10 volumes of T1-

weighted MR image data of each slice 512x512 pix-

els with voxel size 0.39x0.39x2.00mm

. Assessment

is done by computing the Dice coefﬁcient.

Table 1: Comparison of performance with and without ten-

sile force.

Dice’s coefﬁcient

Water ﬂow model Min. Max. Avg.

With tensile force 0.63 0.72 0.68± 0.03

Without tensile force 0.49 0.68 0.62± 0.06

Figure 1: Comparison of performance with and without ten-

sile force.

Since a new tensile component was introduced in

the water ﬂow algorithm, in order to assess its effec-

tiveness, the Dice coefﬁcient was calculated for the

proposed method with and without this component.

Table 1 shows the maximum, minimum and the av-

erage Dice coefﬁcient for 50 hippocampi in the test

set. It can be observed from the table that the tensile

force component plays a positive role in segmenta-

tion and contributes to 6% improvement, on average,

in the Dice coefﬁcient. The dataset (Jafari-Khouzani,

2010) has also been used for assessment of a multi-

atlas (derived from 10 subjects) based method pro-

posed in (Akhondi-Asl et al., 2010) which reports the

UNSUPERVISED 3D SEGMENTATION OF HIPPOCAMPUS IN BRAIN MR IMAGES

185

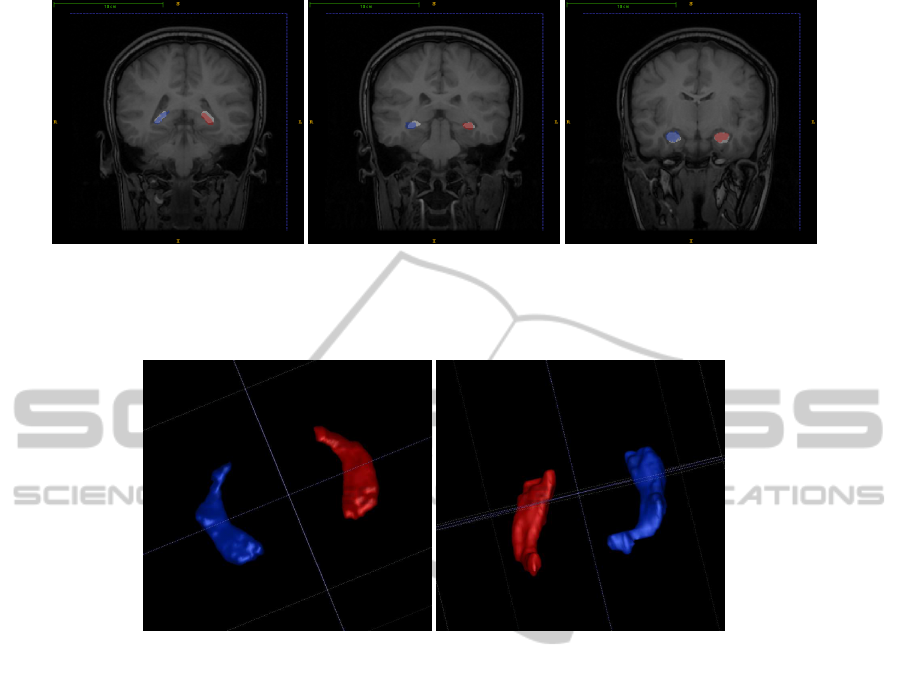
(a) Tail. (b) Body. (c) Head.

Figure 2: Overlay of algorithm output with manual label. Red and Blue translucent regions correspond to algorithm output

and white opaque regions correspond to manual label.

(a) 3D view from hippocampus head. (b) 3D view from hippocampus tail.

Figure 3: 3D surface view of the algorithm output.

average Dice coefﬁcient for the testing part of the

dataset as (0.72± 0.09). This is comparable to that

(0.68 ± 0.03) obtained on the training subset by the

proposed method despite the major difference in the

approaches behind the two methods: multiple atlases

based versus unsupervised method.

Figure 1 provides a graphical comparison of the

Dice coefﬁcient for every volume. The trend of the

two plots is approximately similar. This trend is con-

sistent with the fact that, by design, the tensile force

plays only a moderating role as per (8). In general,

it was observed that the segmentation performance

drops when, even in absence of atrophy, size of hip-

pocampus was very small. In such cases, the corti-

cal walls surrounding the hippocampusand the neigh-

bouring amygdala make the true boundary difﬁcult to

detect resulting in an over-segmentation.

Figure 2 shows some sample extracted hip-

pocampi overlaid over the ground truth. The translu-

cent regions of red and blue denote segmented left

and right hippocampus respectively by the proposed

method. The opaque white region under these corre-

sponds to manual label which is used as the ground

truth. Figure 3 shows the 3D surface view of seg-

mented hippocampi as seen from head of the hip-

pocampus in Figure 3(a) and as seen from its tail in

Figure 3(b).

4 CONCLUSIONS

In this paper, a new method for segmentation of hip-

pocampus in MR volume images is proposed. The

advantage of this method is that it does not require an

atlas or template and is free of parameterisation and

supervision. In spite of its simplicity, this method’s

performance is comparable to existing methods. The

tight variance in the Dice coefﬁcient is particularly

encouraging. These results demonstrate that the

framework of hybrid segmentation can successfully

tap advantages of each of the two stages.

The improvement in segmentation performance

with the addition of the proposed tensile component

to the water ﬂow model indicates that the surface

evolution is constrained yet yields more accurate sur-

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

186

faces. A shortcoming of the proposed methods is that

since the water ﬂow model always evolves from in-

side the region to outside, the coarse segmentation

output has to be within the target boundary of the hip-

pocampus. This limitation can be addressed by de-

signing techniques which permit a two-sided evolu-

tion of the water front.

Overall, it can be concluded that the obtained re-

sults show promise and pave way for applying of

the water ﬂow model for segmenting other (partially)

weak-edge structures as well. Future work will be

targeted at complete automation of this method by

reliable automatic initialisation of seed points or re-

placing the region growing with any other method for

coarse segmentation.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. D.Ravi Varma,

DM, KIMS hospital, Hyderabad for his input towards

anatomical structure of hippocampus and qualitative

analysis of results.

REFERENCES

Ahmed, M., Yamany, S., Mohamed, N., Farag, A., and Mo-

riarty, T. (2002). A modiﬁed fuzzy c-means algorithm

for bias ﬁeld estimation and segmentation of mri data.

Medical Imaging, IEEE Transactions on, 21(3):193 –

199.

Akhondi-Asl, A., Jafari-Khouzani, K., Elisevich, K., and

Soltanian-Zadeh, H. (2010). Hippocampal volume-

try for lateralization of temporal lobe epilepsy: Auto-

mated versus manual methods. NeuroImage, In Press,

Corrected Proof:–.

Akselrod-Ballin, A., Galun, M., Gomori, J. M., Brandt,

A., and Basri1, R. (2007). Prior knowledge driven

multiscale segmentation of brain mri. MICCAI 2007,

4792/2007:118–126.

Bernasconi, N., Bernasconi, A., Caramanos, Z., Antel,

S. B., Andermann, F., and Arnold, D. L. (2003).

Mesial temporal damage in temporal lobe epilepsy: a

volumetric MRI study of the hippocampus, amygdala

and parahippocampal region. Brain, 126(2):462–469.

Chupin, M., Cuingnet, R., Lemieux, L., Lehericy, S., Be-

nali, H., Garnero, L., and Colliot, O. (2008). Fully au-

tomatic hippocampus segmentation discriminates be-

tween alzheimer’s disease and normal aging - data

from the adni database. In MICCAI Workshop on

CAPH.

Hurley, D. J., Nixon, M. S., and Carter, J. N. (2005). Force

ﬁeld feature extraction for ear biometrics. Computer

Vision and Image Understanding, 98(3):491 – 512.

Jafari-Khouzani, K. (2010). Mri data set for hip-

pocampus segmentation by department of di-

agnostic radiology at henry ford hospital.

http://www.radiologyresearch.org/HippocampusSeg

mentationDatabase/.

Liu, X. U. and Nixon, M. S. (2007). Image and volume

segmentation by water ﬂow. In ISVC’07: Proceed-

ings of the 3rd international conference on Advances

in visual computing, pages 62–74, Berlin, Heidelberg.

Springer-Verlag.

Ltjnen, J. M., Wolz, R., Koikkalainen, J. R., Thurfjell, L.,

Waldemar, G., Soininen, H., and Rueckert, D. (2010).

Fast and robust multi-atlas segmentation of brain mag-

netic resonance images. NeuroImage, 49(3):2352 –

2365.

McInerney, T. and Terzopoulos, D. (1999). Topology adap-

tive deformable surfaces for medical image volume

segmentation. Medical Imaging, IEEE Transactions

on, 18(10):840 –850.

Morra, J., Tu, Z., Apostolova, L., Green, A., Toga, A., and

Thompson, P. (2008). Automatic subcortical segmen-

tation using a novel contextual model. MICCAI.

Morra, J., Tu, Z., Apostolova, L., Green, A., Toga, A., and

Thompson, P. (2010). Comparison of adaboost and

support vector machines for detecting alzheimer’s dis-

ease through automated hippocampal segmentation.

Medical Imaging, IEEE Transactions on, 29(1):30 –

43.

Pohle, R., Behlau, T., and Toennies, K. D. (2003). Segmen-

tation of 3d medical image data sets with a combi-

nation of region-based initial segmentation and active

surfaces. Medical Imaging 2003: Image Processing,

5032:1225–1232.

Sabuncu, M. R., Yeo, B. T., Leemput, K., Fischl, B., and

Golland, P. (2009). Supervised nonparametric im-

age parcellation. In MICCAI 2009, pages 1075–1083,

Berlin, Heidelberg. Springer-Verlag.

UNSUPERVISED 3D SEGMENTATION OF HIPPOCAMPUS IN BRAIN MR IMAGES

187