
ADAPTIVE HUMAN TREMOR ASSESSMENT
AND ATTENUATION
Six Degree-of-Freedom Motion Analysis Utilizing Wavelets
Wesley J. E. Teskey, Mohamed Elhabiby and Naser El-Sheimy
Department of Geomatics Engineering, University of Calgary
2500 University Dr. NW, T2N 1N4 Calgary, Alberta, Canada
Keywords: Weighted-frequency Fourier linear combiner (WFLC), Wavelets, Accelerometers, Gyroscopes,
Essential tremor, Parkinson’s disease, Kalman smoothing, Microelectromechanical systems (MEMS).
Abstract: The use of a weighted-frequency Fourier linear combiner (WFLC) algorithm for assessment and attenuation
of movement disorder tremor (including essential tremor and Parkinson’s tremor) is quite prevalent; indeed,
this technique is likely the most popular for such applications. The novel work presented here applies this
technique to accelerometer and gyroscope data describing six degree-of-freedom motion (three translational
and three rotational degrees-of-freedom). Most analysis of tremor is based on observation of generally one
to three degrees-of-freedom of motion. Six degree-of-freedom motion analysis is more difficult to
accomplish because of the complexity of capturing such a large amount of motion data. As well, processing
accelerometer and gyroscope data to yield six degree-of-freedom motion generally involves the use of a
Kalman smoother (necessary because of signal noise and drift) to ensure that accelerometer signals are
correctly compensated for the influence of gravity. After data are processed using a Kalman smoother and
the WFLC algorithm is applied, results are interpreted using wavelet frequency spectrum analysis to
determine the frequency content before and after processing the data. Results show that the WFLC
algorithm can be successfully applied to all six degrees-of-freedom of motion to largely remove tremor.
1 INTRODUCTION
1.1 Movement Disorder Assessment
In recent years there has been much focus on
movement disorder tremor assessment using inertial
sensors (accelerometers and gyroscopes (Rocon, et
al., 2004, 2006)). Such assessment of tremor related
disorders (focussing largely on size of tremor,
frequency, axis of motion etc.) can help to create a
standardized approach to assist medical
professionals when diagnosing tremor; this approach
can help to better understand the nature of the
disorder under evaluation. As well, assessment of
tremor can be used to evaluate the effectiveness of
medication.
1.2 Movement Disorder Attenuation
Attenuation of tremor is another major focus of
recent research conducted. It can take the form of an
orthesis designed to actively remove tremor, or
passive and active feedback systems to dampen and
mitigate tremor (such as a pen with a feedback
system such that the tip moves so as to counteract
tremor motion). Such attenuation can be quite useful
because 90% of tremor patients report a disability
(Gallego, et al., 2009).
1.3 Types of Disorders Evaluated
Tremors types evaluated for this research paper
include essential tremor (ET) and Parkinson’s
disease (PD); these are among the most common
types of tremor disorders (although, sufferers of
these disorders can also exhibit other non-tremor
related symptoms) (Rocon, et al., 2004). ET is the
more prevalent of these two, affecting 4% of people
over age 65 (Louis, 2005); while PD affects 1.5-
2.5% of people older than 70 in the United States
(Mansur, et al., 2007). Tremor is generally regarded
to have a frequency of 3-12 Hz (Elble and Koller,
1990).
46
J. E. Teskey W., Elhabiby M. and El-Sheimy N..
ADAPTIVE HUMAN TREMOR ASSESSMENT AND ATTENUATION - Six Degree-of-Freedom Motion Analysis Utilizing Wavelets.
DOI: 10.5220/0003146900460054
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 46-54
ISBN: 978-989-8425-37-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
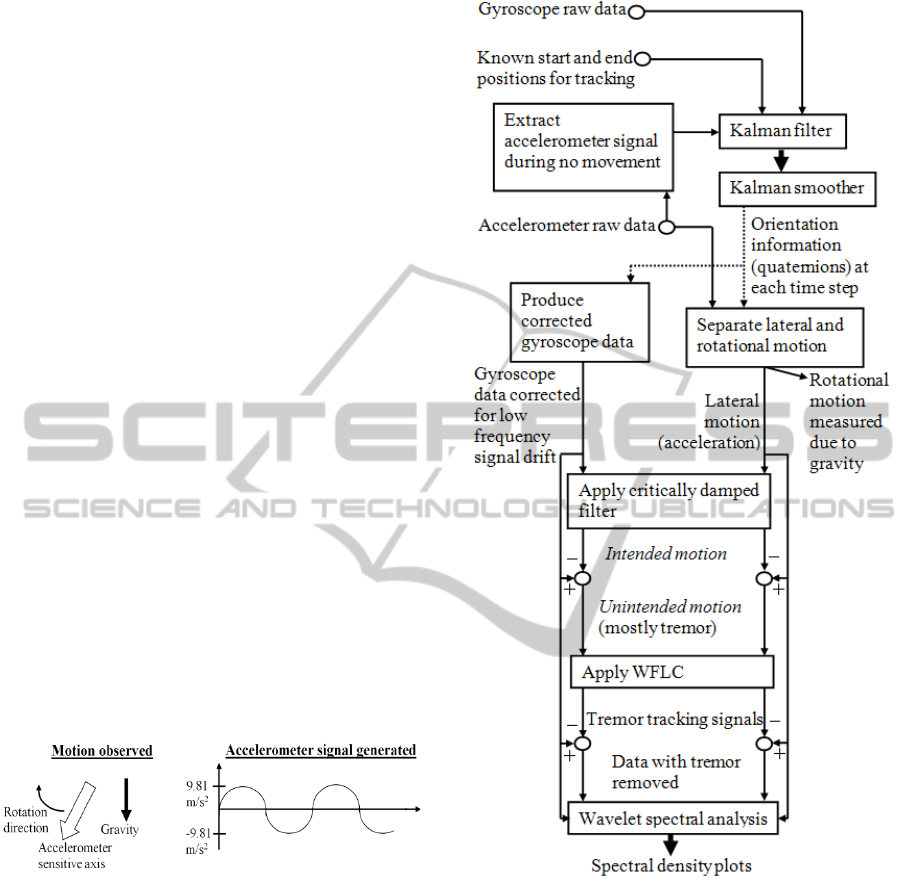
2 IMPORTANCE OF KALMAN
FILTER
When utilizing accelerometers for tremor assessment
and attenuation, it is critical to consider that raw
accelerometer data contain both lateral and
rotational tremor components (Rocon, et al., 2004).
The former tremor type is measured directly by
accelerometers and the later is caused by rotation
through the gravity field. Indeed, rotating an
accelerometer through a gravity field (i.e. about a
vector perpendicular to gravity) at a constant rate
will cause the accelerometer signal to follow a
generally sinusoidal trajectory with peaks at positive
gravitational acceleration (generally approximately
9.81 m/s
2
depending on the local gravity field) and
troughs at negative gravitational acceleration; this is
illustrated in Figure 1. It follows that a rotational
tremor (with no lateral motion component) will also
register an accelerometer signal depicting tremor
motion components. Such a rotational tremor is
removed from accelerometer data in this research
paper so that the lateral acceleration components can
be evaluated independently of rotation. This is
shown in Figure 2, an overall flow chart of the data
processing. From this figure, it can be seen that
processed accelerometer data (bottom half of the
figure on the right hand side) is used to evaluate
lateral tremor and processed gyroscope data (bottom
half of the figure on the left hand side) is used to
evaluate rotational tremor.
Figure 1: An accelerometer rotated through the gravity
field and the signal generated.
To decipher lateral and rotational tremor motion (for
six degree-of-freedom motion resolution), a Kalman
smoother is employed. Strictly speaking, raw
gyroscope data should be sufficient to remove
rotational tremor components from accelerometer
data by providing orientation information; however,
due to signal noise, an accurate solution generally
involves extra information and data fusion to
accurately obtain orientation data. For the Kalman
smoother employed in this research paper, such data
fusion uses the known start and end orientation of
inertial sensors. As well, updates are performed
using accelerometer data during relatively still
Figure 2: Overall flow chart for data processing.
motion signal portions to estimate orientation about
the two horizontal axes (i.e. an orientation reading is
performed using an accelerometer gravity
measurement when the inertial sensors are
stationary).
After Kalman smoothing, the weighted-
frequency Fourier linear combiner (WFLC)
algorithm is used for further analysis. The
application of WFLC for the evaluation of all six
degrees-of-freedom of tremor motion is novel and is
introduced in this research paper likely for the first
time. The WFLC algorithm is generally regarded as
the most useful for both assessment and attenuation
ADAPTIVE HUMAN TREMOR ASSESSMENT AND ATTENUATION - Six Degree-of-Freedom Motion Analysis
Utilizing Wavelets
47

of tremor (Rocon, et al., 2004).
There are many advantages to using the WFLC
technique for six degree-of-freedom tremor analysis.
One is that it can allow for medical professionals
studying tremor to determine the axis of motion for
which tremor is most prevalent for different patients.
It also allows for one to determine the degree of
correlation of different lateral and rotational tremors
and their phase shift with regard to one another.
Another feature important for tremor assessment, the
overall signal shape (i.e. sinusoidal, zigzag etc.) for
each axis of motion, can also be studied.
Six degree-of-freedom motion information is
required to properly attenuate tremor for many
applications; this is often the case when an external
mechanism is used for attenuation (such as implied
by the test setup utilized for the research conducted
and presented here, where patients were told to
simulate eating using a spoon). Such a motion was
chosen for analysis because many tremor patients
complained about to the fact that they often spilled
their soup whilst trying to eat. Studying such a
movement is also useful from the perspective of
assessment in that significant tremor data is present
during evaluation. Future applications stemming
from the research carried out could see actuators
between the spoon head and handle to mitigate
tremor motion.
3 MATHEMATICAL METHODS
3.1 Kalman Filter and Smoother
3.1.1 Kalman Filter
Raw data is first processed to determine sensor
orientation for all six inertial sensors used in data
collection (three accelerometer and three gyroscopes
mounted on a rigid body). The state vector for the
Kalman smoother is given as follows:
=
,
,
,
(1)
Where the first three elements of indirectly
give rotation magnitude about the x, y and z axes,
respectively, and the last element gives the
magnitude of overall orientation. The following
equations can be used to determine the Kalman filter
a priori values of the quaternion vector for
subsequent time steps under evaluation (as found in
(Sabatini, 2006)):
=
,
(2)
and
,
=
,
+
1
2
(
)
(3)
Where is time interval between data readings,
,
is a four by four element identity matrix and the
matrix () is given by:
(
)
=
0−
−
0−
−
−
0−
0
(4)
Elements
,
and
(components of the
vector ) are gyroscope measurements for the x, y
and z axes respectively. The Kalman filter a priori
covariance matrix () for the quaternion state vector
is found for subsequent time steps as follows:
=
,
,
+
1
2
,
(5)
Where
=
−
−
−
−
−
−
(6)
And
,
is a three by three covariance matrix
for gyroscope measurements populated with non-
zero elements along only the main diagonal as in
Sabatini (2006). Values for the matrix are found
using an angular random walk formulation as in El-
Sheimy, et al. (2008), Shin (2005) and Stockwell
(2010).
A standard Kalman filter a posteriori update
procedure is used as in Chui and Chen (1991) and
Grewal (1993). Updates are taken from known start
and end orientations of the inertial sensors and
accelerometer data measurements during periods of
relatively stationary or limited motion (stationary or
limited motion is determined from when
accelerometer signals show low standard deviation
and have a combined signal strength roughly
equivalent to gravity). Such accelerometer gravity
measurements can provide orientation information
for two of the three axes of orientation (the two
lying in the horizontal plane).
3.1.2 Kalman Smoother
After Kalman filtering has finished, a Rauch-Tung-
Striebel (RTS) Kalman smoother is applied as given
in Brown and Hwang (1992) and Shin (2005). This
BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices
48

smoother has the effect of removing discontinuities
in the processed data and improving data quality.
Once orientation data has been found and
smoothed, it can be used to correct accelerometer
signals for gravitational measurements. This is done
by using a rotation matrix at each time step (
) to
transform accelerometer data () (which lie in the
coordinate frame of the moving IMU (Inertial
Measurement Unit)) into a consistent coordinate
frame. Such a consistent coordinate frame is fixed
relative to the earth so that gravity (̅) can be
subtracted from the signal. After gravity is removed,
the remaining accelerometer data are transferred
back into the IMU coordinate frame, as follows:
=
(
−
̅
)
(7)
Where superscript −1 denotes matrix inversion
and
is accelerometer data with only translational
motion components remaining (and not influenced
by gravitational acceleration).
can be found
directly from Kalman smoothed quaternion values
(), as depicted in Altmann (1986) and Kuipers
(1999)). As well, ̅ (a three element vector) will
have values of 0, 0 and −
, respectively, for its x,
y and z axes (where
is the magnitude of
gravitational acceleration) if the consistent
coordinate frame chosen is that of the IMU start
position as depicted in Figure 4 (a).
3.2 Application of the WFLC
Algorithm
3.2.1 Critically Dampened Filter
Processed gyroscope data (raw data with low
frequency error drifts removed) and processed
accelerometer data (with the gravitational influence
on signals removed) are evaluated using a critically
dampened filter. This filter was found to be the best
in estimating intended motion (i.e. motion with
tremor components removed) when compared to a
number of popular alternatives based on its ability to
adequately track a signal without being influenced
by signal components with significant tremor
(Gallego, et al., 2009). The filter effectively uses a
least squares straight line fit of data with more recent
data being given a higher weight (i.e. more influence
on the fitting line parameters) than previous data
(Brookner, 1998).
3.2.2 WFLC Algorithm
The WFLC algorithm fits a series of sinusoidal
signals (harmonic sines and cosines referenced to a
fundamental frequency) to the data under evaluation
(Riviere, et al., 1997). In its early development, it
was used for removing the tremor of a surgeon’s
hand during critical operations by using a feedback
system and electric actuators within a surgical
instrument to counteract tremor (Riviere, et al.,
1998). The algorithm also is quite useful for
describing and removing movement disorder tremor
because of its ease of implementation (i.e. simplistic
mathematical iterations are utilized), zero phase lag
real time filtering capabilities and its relative
computational efficiency (utilizing just a small
number of iterative computational steps).
3.3 Wavelet Spectral Analysis
Pre and post WFLC processed inertial data (both
with gravitational effects on accelerometer data
removed) are analyzed using wavelets to determine
the frequency spectrum. The main advantages of
using wavelets for such an application is the
localization power in both frequency and time
domain (so non tremor signal portions between trials
can be easily negated) and the availability of
numerous base functions, that can be used as mother
wavelet function, leading to better signal modelling;
as opposed to Fourier based analysis which is
largely focussed on the use of sinusoidal functions
for analysis.
A continuous wavelet transform was used to
allow for a more thorough visual inspection of the
signal evaluated than can be afforded using a
discrete wavelet transform. The continuous wavelet
transform is found as follows (Goswami and Chan,
1999):
,
=
()
(
)
(8)
Where
is a scaling coefficient to allow for
analysis of different frequencies of interest,
is a
time shift parameter that allows for localization of
the analysis,
(
)
is the inertial signal under
evaluation at time and
is the mother wavelet
analyzing function’s complex conjugate. Wavelet
scales selected (given as in (8)) for evaluation span
1 to 64 (with corresponding pseudo-frequencies of
91.8 Hz and 1.4 Hz respectively; these pseudo-
frequencies are found by scaling the wavelet center
frequency (Matlab, 2008)). Such a broad frequency
spectrum for analysis allows for an in depth view of
the signal under examination.
A coiflets wavelet of order three was used for
evaluation because it matched closely with the data
when compared to other possible wavelet candidate
ADAPTIVE HUMAN TREMOR ASSESSMENT AND ATTENUATION - Six Degree-of-Freedom Motion Analysis
Utilizing Wavelets
49

functions. The coiflets 3 mother wavelet is shown in
Figure 3.
4 EXPERIMETNAL METHODS
AND RESULTS
4.1 Data Collection
Figure 4 depicts the manner in which data was
collected from test subjects (note the IMU axes
labels in Figure 4 (a)). Test subjects lifted an IMU
out of a holster and simulated eating using a spoon
attached to the IMU (simulating only one placement
of food into their mouth). Upon completion of this
task, the returned the IMU to the holster; ten such
tests were carried out for each subject under
evaluation. In this manner, both the start and end
orientation of the IMU were known (relative to one
another) which is important for implementation of
the Kalman filter and smoother depicted in sub-
section 3.1.
Figure 3: The coiflets 3 mother wavelet.
Data logging took place at 130 Hz. The IMU
used was manufactured by the Mobile Multi-Sensor
Systems (MMSS) research group at the University
of Calgary. A tri-axial accelerometer (LIS3L06AL
from ST Microelectronics (2006)) and three single-
axis gyroscopes (XV-8100CV from Epson Toyocom
(2010)) were utilized.
During experimentation, 11 controls (7 female), 9
ET patients (3 female) and 30 PD patients (20
female) were evaluated using testing that had
received ethics approval from the Conjoint Health
Research Ethics Board at The University of Calgary.
The mean age of controls was 64.1, for ET patients
it was 64.8 and for PD patients it was 66. A number
of patients (2 ET and 27 PD) were on medication to
help reduce tremor. For the ET patients, this
medication was largely ineffective (based on
conversation with the patients and results of the data
analysis presented here) and for PD patients it had
varying effectiveness depending on when they last
took their medication and how large the dosage was.
Patients with the most significant tremor (8 of
the ET patients and 9 PD patients) were evaluated
separately for the analysis in the following sections
of this research paper. These patients were selected
based on a thresholding criteria that required their
tremor to be one standard deviation in excess of the
tremor measured for controls (for at least one of the
six inertial signals evaluated), based on the mean
absolute value of wavelet details coefficients at scale
18 (corresponding to approximately 5.1 Hz). A
higher value for details coefficients suggested more
tremor motion was present. Test subjects that did not
pass this thresholding criteria produced data that
largely resembled that of controls and therefore such
data is not displayed in the following sections of this
research paper.
Figure 4 (a): A test subject prior to evaluation.
Figure 4 (b): A test subject during evaluation.
x-axis
y-axis
z-axis
BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices
50

4.2 Kalman Smoothing and WFLC
The Kalman smoothing algorithm was very effective
in removing gravitational readings from
accelerometer signals. A representative example of
this is shown in Figure 5 for a control.
It is important to note that the raw data signal in
Figure 5 has extended periods of time in which it is
continuously a long distance from the zero
acceleration mark. This is expected because
gravitational readings can influence the sensors,
depending on their orientation. When gravity’s
impact is removed, the signal remaining only has
short durations when it is not near the zero
accelerometer reading. This illustrates the value of
using the algorithm outlined because the remaining
accelerometer data, for the most part, only have
lateral motion information embedded within them,
making subsequent data analysis significantly more
useful than if raw data were used.
Figure 5: An x-accelerometer signal before and after
Kalman smoothing to remove gravitational readings.
After accelerometer signals are corrected as
depicted in Figure 5, they are analysed (along with
processed gyroscope data) using a critically
dampened filter. The goal is to estimate the intended
motion of the test subjects under evaluation. The
results for this are shown in Figure 6 for an ET
subject. Generally, the critically dampened filter
performed quite well and was a very efficient filter
for estimating intended motion of test subjects. One
issue that if unavoidable with such a filter is that if
the influence of past measurements if kept high (in
the least squares sense), the filter will lag the signal
under evaluation; however, if the influence of past
measurements is reduced, then the filter does not
remove all tremor motion components. A balance
needs to be struck to ensure both adequate tracking
and tremor removal are achieved. The results given
in Figure 6 are generally representative of results for
all inertial data when a subject with high tremor is
evaluated. In this case, a small amount of residual
tremor remains in the processed signal; but the
ability of the critically damped filter to track the
signal adequately, so as to approximate intended
motion, is reasonable.
After the critically damped intended motion
approximation is removed from the signal, the
remaining signal portion can be evaluated using the
WFLC algorithm. Application of this algorithm
required a two stage iteration at each time step, the
first iteration was used to find the fundamental
frequency of the tracked signal and the second
iteration was used to find the numerical weights for
sinusoids tracking the signal. Multiple iterations
were sometimes required at the same time step to
allow the algorithm to sufficiently converge to a
solution (particularly with the gyroscope data which
had a large dynamic range). A representative sample
for the WFLC motion approximation is shown in
Figure 7; it is a close up of a signal portion of the
data displayed in Figure 6.
Figure 6: A processed z-gyroscope signal before and after
a critically damped filter is applied to approximate
intended rotational motion.
It is clear from Figure 7 that the WFLC
algorithm tracks tremor quite well. The result
depicted is quite typical for all inertial data
evaluated. Given such an approximation of the
tremor, it is possible to very precisely pinpoint the
frequency of the tremor observed and its magnitude.
This is useful for assessment because it allows for
medical professional to evaluate how tremor varies
between patients and for the same patient before and
after medication is taken.
ADAPTIVE HUMAN TREMOR ASSESSMENT AND ATTENUATION - Six Degree-of-Freedom Motion Analysis
Utilizing Wavelets
51

Figure 7: A processed z-gyroscope signal portion and its
WFLC approximation depicting rotational motion.
For the purposes of attenuation, the WFLC
algorithm provides the signal to be removed from
motion to mitigate tremor. The WFLC algorithm is
especially useful for attenuation because its zero
phase lag property allows for accurate and real time
tremor suppression which is critical for many
attenuation applications.
4.3 Wavelet Spectral Analysis
Signals can be compared before and after removal of
WFLC tremor components to evaluate their
frequency spectrum. Such an analysis can assist one
in understanding what components of motion have
been removed and whether tremor frequencies of
interest have been adequately targeted (3-12 Hz). It
also helps one to understand how useful the WFLC
algorithm is for assessment by depicting how well
the tremor motion can be tracked.
In Figure 8, the results of applying the
continuous wavelet transform to the signal in Figure
6 (with the critically dampened portion of motion
removed) are shown; lighter colours depict that more
frequency content is present.
When comparing Figure 8 to Figure 6, it is clear
that when a great deal of tremor motion is present,
the amount of signal energy depicted in the 3-12 Hz
frequency band increases significantly. Thus, Figure
8 validates the use of a coiflets 3 wavelet for the
application undertaken (given that other inertial
signals processed gave similar results).
Figure 8: Wavelet processed z-gyroscope data (only
unintended tremor motion is processed for rotational
movement).
The overall (population) results for the data
analyzed are given in Figures 9 and 10 for a
representative accelerometer axis of motion and
gyroscope axis of motion, respectively. Tellingly,
the results for all three accelerometer axes of motion
were very similar as were the results for all three
gyroscope axes of motion. This tends to indicate that
tremor acts along all axes of motion concurrently
and also that it can be removed in a similar fashion
(using the critically dampened and WFLC
algorithms) for all of these axes. The results depicted
were found by taking the mean magnitude of details
coefficients at each wavelet scale for all test subjects
of a particular group.
Figure 9: x-accelerometer wavelet spectral analysis for
lateral tremor
It can be seen from the results in Figures 9 and
10 that the frequency of the tremor measured for
both ET and PD patients was within the expected 3-
12 Hz range (as depicted by a bulge in the data
displayed within this band). ET patients generally
BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices
52
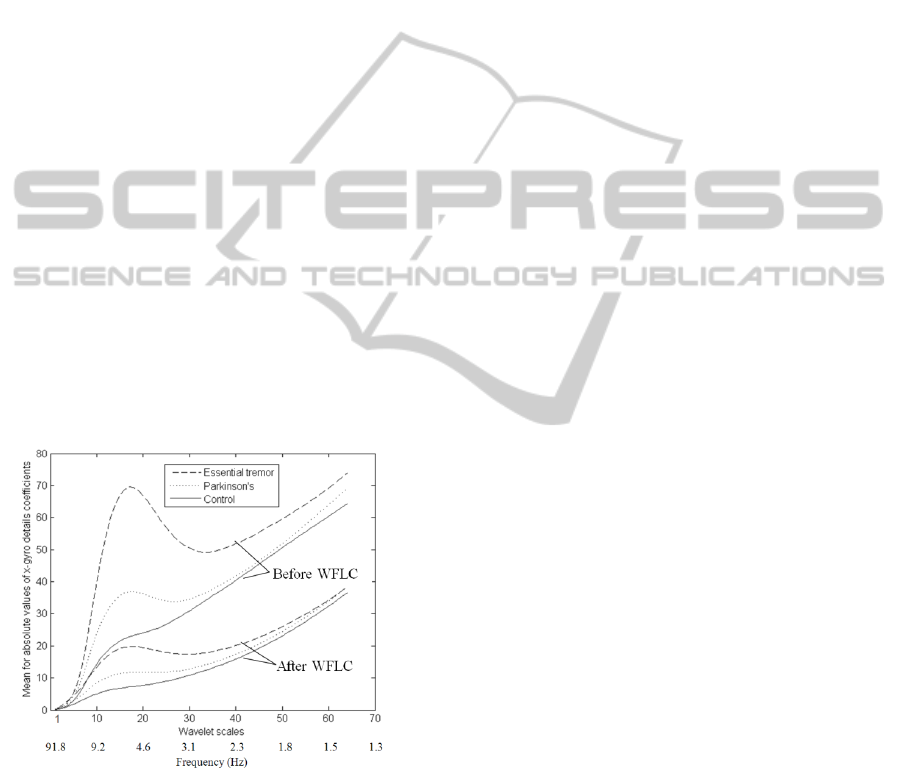
depicted more tremor that PD patients, which
corresponds well to the fact that most ET patients
were not on medications for treatment while most
PD patient were.
Tremor was reduced substantially for all three
groups examined (ET, PD and control) when the
WFLC algorithm was applied and it decreased in a
proportionate manner, such that those with more
tremor before processing also had more frequency
content remaining in their motion after application
the WLFC algorithm. Signal noise was also likely
reduced inadvertently. One of the more significant
results is that in the 3-12 Hz range, all three groups
evaluated with the WFLC technique had less tremor
after evaluation than the control group had before
evaluation.
One unfortunate drawback of the analysis is that
it seems to remove a lot of low and high frequency
motion (as is evident in Figures 9 and 10) along with
the 3-12 Hz frequency band of interest.
The high frequency motion likely represents
jerky motion, such as when a subject inadvertently
struck the IMU on the table during testing. Likely,
for mechanical attenuation applications, some kind
of thresholding criteria will need to be applied to
ensure such signal spikes are not processed, because
mitigation of such motion is likely unrealistic due to
limits in the operation range of mechanical
equipment.
Figure 10: x-gyroscope wavelet spectral analysis for
rotational tremor.
The low frequency motion removed likely
represents the inadequacy of the critically dampened
filter in tracking intended motion. Determining
which motion is desired and which is not is a very
difficult research challenge that has been studied for
many years (Rocon, et al., 2004). Clearly, there still
remains some work to be done to find and
appropriate algorithm that is adequately
computationally fast and has zero phase lag.
5 SUMMARY
AND CONCLUSIONS
The analysis performed validated the use of the
Kalman smoothing scheme depicted for removal of
the gravitational influence on accelerometer signals.
This was necessary so that accelerometer data would
properly depict the lateral motion under
consideration.
The most significant finding of this research
paper is that a combination of a critically dampened
filter and the WFLC technique adequately removed
the tremor components of motion within the 3-12 Hz
frequency band; this was likely applied for the first
time in six degrees-of-freedom for movement
disorders in this research paper. The same procedure
was applied to all motion axes with quality results in
all cases.
Another significant finding of this research paper
is that the wavelet analysis performed was well
suited for the evaluation of a frequency spectrum.
The coiflets 3 wavelets was quite capable of
realizing tremor motion components, and provided a
useful tool for identifying motion at frequencies of
interest.
ACKNOWLEDGEMENTS
Thanks to Dr. Brian MacIntosh and Bruce Wright
for their help with obtaining lab space, ethics
approvals and the appropriate equipment. Thanks
also to the following funding agencies: Alberta
Innovates – Technology Futures (formerly the
Alberta Ingenuity Fund), the Natural Sciences and
Engineering Research Council of Canada (NSERC)
and Geomatics for Informed Decisions (GEOIDE).
Further thanks to volunteer subjects and the Mobile
Multi-Sensors Systems (MMSS) research group at
the University of Calgary.
REFERENCES
Altmann, S. L., 1986. Rotations, Quaternions and Double
Group. Dover Publications.
Brookner, E., 1998. Tracking and Kalman filtering made
easy. John Wiley & Sons, Ltd.
ADAPTIVE HUMAN TREMOR ASSESSMENT AND ATTENUATION - Six Degree-of-Freedom Motion Analysis
Utilizing Wavelets
53

Brown, R. G., Hwang, P. Y. C., 1992. Introduction to
Random Signals and Applied Kalman Filtering. John
Wiley and Sons Inc. 2
nd
edition.
Chui, C. K., Chen, G., 1991. Kalman Filtering With Real
Time Applications. Springer-Verlag. 2
nd
edition.
Elble R J, Koller W C. Tremor. Baltimore: The John
Hopkins University Press; 1990.
El-Sheimy, N., Hou, H., Niu, X, 2008. Analysis and
modeling of inertial sensors using Allan variance.
IEEE Transactions on Instrumentation and
Measurement, 57(1), pp. 140-149.
Gallego, J. A., Rocon, E., Roa, J. O., Moreno, J. C.,
Koutsou, A. D., Pons, J. L., 2009. On the use of
inertial measurement units for real-time quantification
of pathological tremor amplitude and frequency. In
Proceedings of the Eurosensors XXIII conference.
Procedia Chemistry 1, pp. 1219–1222.
Goswami, J. C., Chan, A. K., 1999. Fundamentals of
Wavelets: Theory, Algorithms and Applications.
Wiley Series in Microwave and Optical Engineering,
Wiley-Interscience.
Grewal, M. S., 1993. Kalmen Filtering: Theory and
Practice. Prentice-Hall.
Kuipers, B. J., 1999. Quaternions and Rotation Sequences:
A Primer With Applications to Orbits, Aerospace and
Virtual Reality. Princeton University Press.
LIS3L06AL MEMS Inertial Sensor Data Sheet, 2006. ST
Microelectronics, pp. 1-17, [Online]. Available: http://
www.st.com/stonline/products/literature/ds/11669.pdf
[Accessed 13 July, 2010].
Louis, E. D., 2005. Essential tremor. Lancet Neurol, 4, pp.
100-110.
Mansur, P. H. G., Cury, L. K. P., Andrade, A. O., Pereira,
A. A., Miotto, G. A. A., Soares, A. B., Naves, E. L.
M., 2007. A Review on Techniques for Tremor
Recording and Quantification. Critical Reviews in
Biomedical Engineering, 35(5), pp. 343-362.
Matlab (computational environment) Help
Documentation, 2008. scal2frq function, [Online].
Available:http://matlab.izmiran.ru/help/toolbox/wavel
et/scal2frq.html [Accessed 13 July, 2010].
Riviere, C. N., Rader, R. S., Thakor, N. V., 1998.
Adaptive Canceling of Physiological Tremor for
Improved Precision in Microsurgery. IEEE
Transactions on Biomedical Engineering, 45(7), pp.
839-846.
Riviere, C. N., Reich, S. G., Thakor, N. V., 1997.
Adaptive Fourier Modeling for Quantification of
Tremor. Journal of Neuroscience Methods, 74, pp. 77-
87.
Rocon, E., Belda-Louis, J. M., Sanchez-Lacuesta, J. J.,
Pons, J. L., 2004. Pathological Tremor Management:
Monitoring, Compensatory Technology and
Evaluation. Technology and Disability, 16, pp. 3-18.
Rocon de Lima, E., Andrade, A. O., Pons, J. L., Kyberd,
P., Nasuto, S. J., 2006. Empirical Mode
Decomposition: a Novel Technique for the Study of
Tremor Time Series. Med Bio Eng Comput, 44, pp.
569- 582.
Sabatini, A. M., 2006. Quaternion-based extended Kalman
filter for determining orientation by inertial and
magnetic sensing. IEEE Transactions on Biomedical
Engineering, 53(7), pp. 1346-1356.
Shin, E., 2005. Estimation Techniques for Low Cost
Inertial Navigation. Ph.D. Department of Geomatics
Engineering, University of Calgary.
Stockwell, W., Angle Random Walk. Crossbow
Technologies Inc., pp. 1-4, [Online]. Available: http://
www.xbow.com/pdf/AngleRandomWalkAppNote.pdf
[Accessed 13 July, 2010].
XV-8100CB ultra miniature size gyro sensor data sheet.
Epson Toyocom, pp. 1-2, [Online]. Available:
http://www.frank-schulte.com/media/Pdf/XV-
8100CB_E06X.pdf [Accessed 13 July, 2010].
BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices
54
