USING GRANGER CAUSALITY TO CHARACTERISE

BIDIRECTIONAL INTERACTIONS IN THE HUMAN BRAIN

DURING INDUCTION OF ANAESTHESIA

Nicoletta Nicolaou, Julius Georgiou

Holistic Electronics Research Lab, KIOS, Dept. of Electrical and Computer Engineering

University of Cyprus, Kallipoleos 75, 1678 Nicosia, Cyprus

Saverios Houris, Pandelitsa Alexandrou

Anaesthesiology Department, Nicosia General Hospital, 215 Old Nicosia-Limassol Rd, 2029 Nicosia, Cyprus

Keywords: Anaesthesia monitoring, Electroencephalogram, Granger causality, Synchronisation, Bidirectional

interaction.

Abstract: General anaesthesia is a reversible state whereby conscious experience is disrupted and reflexes to afferent

stimuli are depressed. The precise method of action of anaesthetic agents is still largely unknown. However,

the administration of anaesthetics causes observable changes in the electrical brain activity (EEG), the study

of which can provide an insight into the mechanism of action of general anaesthesia. This paper investigates

the patterns of bidirectional interactions that are manifest in brain activity during anaesthetic induction with

propofol. Granger Causality is applied to the EEG of patients scheduled for surgery under general

anaesthesia as a means of characterising the interactions between different brain areas prior and after the

administration of the anaesthetic agents. Strong unidirectional information flow between frontal and

posterior areas was found to occur shortly after anaesthetic induction.

1 INTRODUCTION

General anaesthesia (GA) is a reversible state of

unconsciousness and depression of reflexes to

afferent stimuli, induced by the administration of

chemical agents (Hammeroff, 2006). Desirable

supplements of it include immobility (analgesia),

loss of conscious awareness and amnesia. Since the

mechanism by which consciousness emerges is still

not fully understood, the mechanism by which

general anaesthetics prevent consciousness is also

largely unexplained. One approach to understanding

this critical mechanism is to look for invariant

changes that manifest themselves in observables of

the human brain, such as the electroencephalogram

(EEG), as patients lose and regain consciousness

under the effect of various anaesthetic agents. The

appearance of spindle-like waves and background

slow δ (1.5-3.5Hz) activity is probably the most

prominent EEG sign of GA (Bennett et al., 2009). In

general, the EEG shows signs of decreased fast

activity (α and β rhythms) and increase of the slow

and large-amplitude δ and θ components as the

depth of anaesthesia increases. In very deep

anaesthesia the EEG may develop a peculiar pattern

of activity known as burst suppression, during which

alternating periods of normal to high activity and

low voltage (or even isoelectricity) are observed

(Rampil, 1998).

The changes in the EEG observed under GA are

also important for monitoring the depth of

anaesthesia. Lately devices that monitor the depth of

anaesthesia are utilised during surgery to provide

additional information concerning the general state

of hypnosis of the patient, including anaesthetic

overdose or even potential regaining of

consciousness during surgery. The latter is a serious

concern as the incidence of awareness ranges from

as low as 0.11% for general surgery (Ranta, 2002),

up to an astonishing 20% for trauma surgery (Myles

et al., 2003). The rates of awareness are affected by

a number of factors, such as the patient gender, the

type of surgery, the anaesthetic agent administered,

faults in the anaesthetic apparatus, and individual

188

Nicolaou N., Georgiou J., Houris S. and Alexandrou P..

USING GRANGER CAUSALITY TO CHARACTERISE BIDIRECTIONAL INTERACTIONS IN THE HUMAN BRAIN DURING INDUCTION OF

ANAESTHESIA.

DOI: 10.5220/0003148601880194

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 188-194

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

differences in pharmacokinetics (Ranta, 2002, Myles

et al., 2003). This is one of the most distressing

aspects of surgery as in the majority of times the

patients are unable to alert the anaesthetist that they

have regained consciousness during surgery, and are

in pain, due to the routine co-administration of

neuromuscular blocking agents with the anaesthetic

agents.

The most widespread commercial monitors of

hypnosis currently in use are the BIS monitor

(Aspect Medical Systems, Natick, MA) (Sigl and

Chamoun, 1994) and Datex-Ohmeda S/5

Entropy

Module (originally by Datex-Ohmeda Division,

Instrumentation Corp., Helsinki; now with GE

Healthcare) (Viertiö-Oja et al., 2004). Such devices

operate by extracting a number of features from the

EEG in order to deduce the relative depth of

hypnosis, which is then easily visualised as a

number from 0-100 (100: fully awake, 0: no

activity). Even though these devices offer additional

support to the work of the anaesthetist, they still

suffer from some important reliability issues

(Russell, 2006, Barr et al., 1999, Dahaba, 2005,

Messner et al., 2003).

The main reason behind some of the problems

faced by existing monitors can be pinpointed to the

fact that they utilise a number of empirical measures

from the EEG, which are then combined in a

proprietory way into a single number denoting the

depth of anaesthesia. The information utilized is,

thus, representative of the characteristics of the

observed activity and not of the physiological

process that occurs during anaesthesia. Strong

evidence for this provide reported incidences of

awareness despite monitors displaying adequate

depth of anaesthesia (Rampersad and Mulroy, 2005,

Mychaskiw et al., 2001), and the inability of some

monitors to distinguish between the EEG of an

anaesthetized patient and the EEG of somebody who

is asleep (Russell, 2006, Sleigh et al., 1999). The

latter is not surprising considering that sleep and

anaesthesia share some common mechanisms (Voss

and Sleigh, 2007). However, despite the large

similarities, there are fundamental differences in the

particular physiological mechanisms of the two

processes which a true monitor of anaesthetic depth

should be able to identify. Thus, a successful

monitor should extract information from the

observed activity that is representative of the deeper

interactions and which reflects the physiological

changes that occur from administration of the

anaesthetic agents as these are manifest in the

observed activity. In other words, the measures

utilised must be based on ‘neurobiologic phenomena

that represent the necessary and sufficient conditions

for consciousness in a specific individual’ (Hudetz,

2008).

In recent years it has been shown that measures

which characterise the interactions between different

brain areas can provide an insight into how

integration of information is achieved in the brain

during various cognitive tasks. One such measure is

Granger causality, a linear measure quantifying the

bidirectional interaction between two time series.

Even though Granger causality has provided useful

information from EEG activity in a number of

applications (see (Pereda et al., 2005) and references

within), it has yet to be applied in the study of

general anaesthesia. In this work, the interactions

between different brain areas during induction of

anaesthesia are investigated using Granger causality.

Anaesthetic induction is important as one can readily

study the point of loss of consciousness that occurs

from the administration of a bolus of anaesthetic

agent. Such information is important in subsequent

monitoring of anaesthetic depth and identification of

potential regaining of consciousness during surgery.

2 METHODOLOGY

2.1 Dataset

The data has been collected from 10 male patients

(mean age 34.6±18) undergoing general and

urological surgery at Nicosia General Hospital,

Cyprus. The study has been approved by the Cyprus

National Bioethics Committee and patients gave

written informed consent for their participation.

Participants were not taking any medication acting

on the central nervous system and were of normal

weight. EEG data was collected using the 24-

channel configuration of the TruScan32 system

(Deymed Diagnostic) at a sampling rate of 256Hz.

Electrodes were placed at positions Fp1, Fp2, F7,

F3, Fz, F4, F8, T3, C3, Cz, C4, T4, T5, P3, Pz, P4,

T6, O1 and O2, according to the International 10/20

system. Data was recorded with an FCz, and ground

was located on the head. No filtering was performed

during data collection. Data recording commenced

while patients were still awake prior to

administration of the anaesthetic agents, continued

through loss of consciousness, during the entire

surgery, and until patients regained consciousness at

surgery end. During the recording event markers

were manually inserted to indicate important events,

such as administration of anaesthetic agents.

USING GRANGER CAUSALITY TO CHARACTERISE BIDIRECTIONAL INTERACTIONS IN THE HUMAN

BRAIN DURING INDUCTION OF ANAESTHESIA

189

GA was administered by the anaesthetist in

charge following standard procedures. All patients

were preoxygenated prior to anaesthesia induction

with a propofol bolus. During induction boluses of

fentanyl (for analgesia) and varying quantities of

neuromuscular blocking agent (cisatracurium) were

also administered. Maintenance of GA was achieved

with a constant intravenous administration of

propofol at concentrations ranging between 20-

40ml/h, except in 1 patient were sevoflurane was

used for maintenance. Given that data collection was

performed during actual surgery, propofol

concentrations for induction varied based on specific

patient characteristics and the type of subsequent

surgery.

In these investigations we are only interested in

studying induction of anaesthesia, and subsequently

the point at which patients lose consciousness. Loss

of consciousness was defined as the point at which

the patient stopped responding verbally to

commands by the anaesthetist and occurred some

seconds after administration of the anaesthetic bolus.

2.2 Granger Causality

The investigation of causal relationships is of great

interest, particularly when dealing with

neurophysiological data. Granger Causality (GC)

has been developed explicitly tailored to allow

inferences about causality between two time series

to be made (Granger, 1969). Wiener defined

causality as: “for two simultaneously measured

signals, if one can predict the first signal better by

incorporating the past information from the second

signal than using only information from the first one,

then the second signal can be called causal to the

first one” (Wiener, 1956). This was later given a

mathematical formulation by Granger through the

use of univariate and bivariate autoregressive

models (AR). According to Granger: for two signals,

A, and B, if A is influenced by B, then the addition of

past values of B in the regression of A will improve

its prediction. This can be assessed from the

variances of the prediction errors of the fitted

univariate and bivariate AR models.

For the univariate case,

()

)()(

teitacta

+−=

∑

(1)

()

)()(

teitbctb

+−=

∑

(2)

where

(

)

biai

are the estimated univariate AR

coefficients for the AR model of order P, and

)(

are the residuals (prediction errors) of the AR

process. For the bivariate AR case,

() ()

)()(

teitbditacta

abi

+−+−=

∑∑

(3)

() ()

)()(

teitaditbctb

bai

+−+−=

∑∑

(4)

where

(

)

abiabi

and

)(

baab

are as for the

univariate AR case. Granger Causality can then be

defined as:

ABA

→

(5)

If by using past values of B the prediction of A is

improved, then the variance of the prediction errors

of the bivariate AR model,

()

abABA

evar

, will

be smaller than the variance of the univariate AR

model,

(

)

aAA

evar

. Thus,

→

will

increase. If, however, the past of B does not improve

the prediction of A, then

_/ ABAAA

σσ

≈

, and

→

will be close to zero. Similarly,

→

defined accordingly. If both

→

and

→

are high, then this indicates a bidirectional coupling

or feedback relationship between A and B.

In order to characterise the direction and strength

of coupling between A and B one can look at the

difference between the GC values:

BAAB

GCGCD

→→

−

(6)

⎩

⎨

⎧

→<

→>

stronger is coupling ofstrength ,0

In this way, changes in the direction of coupling can

be readily identified by following the changes in the

sign of D. However, if D is close to zero, then one

can deduce that there either exists bidirectional

coupling of similar strength or no coupling at all. In

this case, one must look at the individual GC values

to identify which of the two scenarios holds.

In the following investigations AR models of

order 6 were utilised. This choice was guided both

by the literature (Tseng et al., 1995, Vaz et al., 1987)

and by preliminary investigations which showed that

the use of higher order models did not have an effect

on the results.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

190

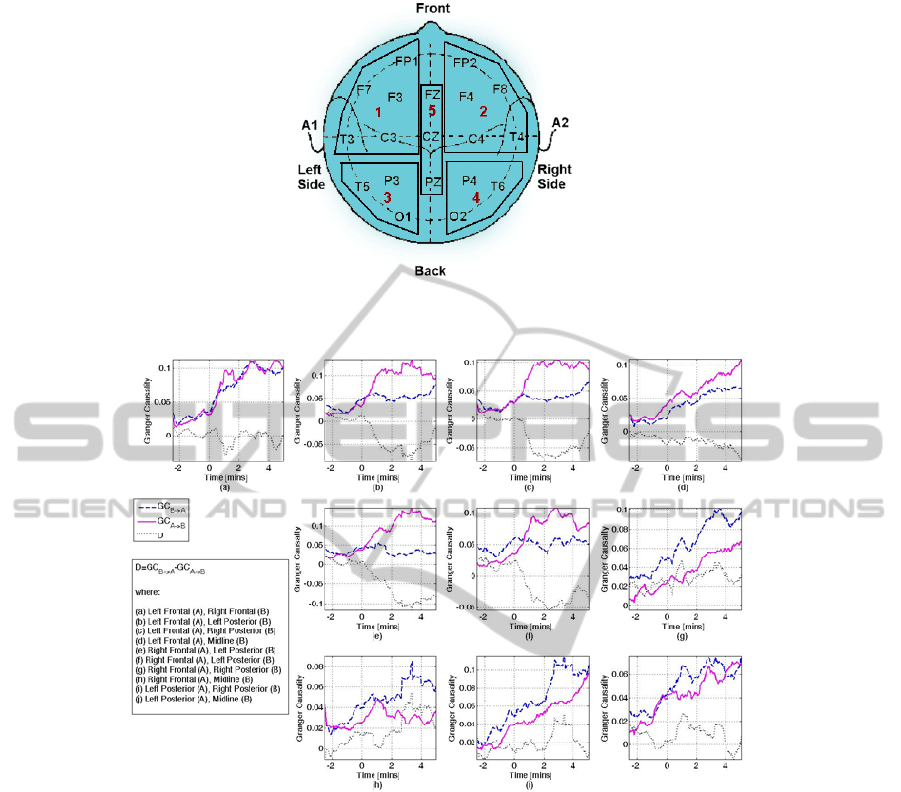
Figure 1: The five brain areas defined and the electrodes contained in each grid. The brain areas were left (grid 1) and right

(grid 2) frontal area, left (grid 3) and right (grid 4) posterior area, and midline area (grid 5).

Figure 2: This figure shows the changes in the direction of coupling, estimated as the difference between

→

and

→

. The legend indicates which area is considered as B and which as A in each of the individual plots. The x-axis

shows time in minutes, where t=0 denotes the point at which the anaesthetic agent was administered. Patient was awake for

t<0, and asleep for t>0. For example, plot (c) denotes the GC between Left Frontal (A) and Right Posterior (B). Thus, the

solid line corresponds to

riorRightPostelLeftFronta

→

, the dashed line to

lLeftFrontariorRightPoste

→

and the dotted line to

riorRightPostelLeftFrontalLeftFrontariorRightPoste

GCGCD

→→

−=

. In this case, a strong unidirectional coupling from the left

frontal area to the right posterior area is observed after anaesthetic induction. Note the different y-axis scales.

3 RESULTS AND DISCUSSION

To assess the interactions between different brain

areas, five electrode grids were first defined (see

figure 1). Each electrode grid represents the gross

activity from each of the following brain areas: left

and right frontal, left and right posterior, and midline

area. The activity of each of these areas is estimated

as the average activity from the electrodes contained

within the specified electrode grid. For some

subjects not all electrodes were available.

Specifically, the following electrodes were

unavailable: (1) S1: P4, T6, Pz; (2) S2: C3, O1; (3)

S3: P3, P4, T6, O2, Cz; (4) S4: T5; and (5) S5: Cz.

The EEG segments extracted were of 8-minute

duration, where 3mins are prior to and 5mins are

after induction, based on the event markers

USING GRANGER CAUSALITY TO CHARACTERISE BIDIRECTIONAL INTERACTIONS IN THE HUMAN

BRAIN DURING INDUCTION OF ANAESTHESIA

191

Figure 3: Granger causality between left frontal (A) and right posterior (B) for a single subject, and their difference, D, prior

and after induction of anaesthesia (at time t=0). Prior to anaesthetic induction GC indicates weak interactions between the

two areas. However, administration of anaesthesia induces strong unidirectional interaction from the left frontal to the right

posterior area. This is reflected as a change in the sign of D.

indicating administration of anaesthesia in each

patient record. Each 8-minute segment is then split

into 2-second non-overlapping windows and

Granger causality is estimated for each window. No

artefact removal has been performed as averaging

removes the effect of some artefacts present in the

data. In addition, after anaesthetic induction there is

minimal presence of artefacts as the patient is not

moving and surgery has not yet commenced.

Figure 2 shows the interactions between the

different brain areas as characterised by Granger

causality and the difference, D (equation 6). The

results shown are averaged over all subjects and a

moving average of order 20 has been applied for

better visualisation. Changes in the sign of D

indicate a change in the direction of interaction.

Whether D is positive or negative depends on which

brain area is taken as B and which area as A. Thus,

the actual sign of D is not important, but the change

in the sign is: negative values indicate a stronger

interaction from A to B, and vice versa for positive

values.

A clear change in the direction of interactions

before and after induction of anaesthesia is

observed. All changes in the GC values at pre- and

post-induction are statistically significant (ANOVA

F-test, α=0.05, p=0; except for GC from LP to RP,

where p=0.03). While the patients are awake, weak

interactions between all brain areas can be observed,

resulting into values of D around zero. The

administration of the anaesthetic agent increases the

strength of interactions in all directions, except of

interactions from posterior to all other areas, which

remain at the same level as prior to anaesthetic

induction. The most striking change related to

anaesthetic induction is the strong unidirectional

inter- and intra-hemispheric interactions from frontal

to posterior areas (fig.2 (b), (c), (e), (f)). These

interactions start occurring approximately 20-30

seconds after induction, thus there is strong reason to

hypothesize that they indicate the point of loss of

consciousness. The strongest interactions are

observed from the left and right frontal areas to the

left posterior area. Figure 3 shows the interaction

between left frontal and right posterior area for a

single subject, whereby this switch of the direction

of interaction induced by administration of the

anaesthetic agent is clear. An increase in the strength

of interaction from midline to all other areas is also

observed, indicated by the positive D values (fig.2

(d), (g), (i), (j)). Anaesthetic induction also induces

strong bidirectional intra-hemispheric frontal

interactions (fig.2 (a)), which are not mirrored in the

posterior areas (fig.2 (h)). In general, administration

of anaesthesia appears to increase information flow

from frontal to posterior areas and from midline to

all other areas.

The lack of strong unidirectional interactions

while the patient is awake is a direct reflection of the

lack of generalised ‘synchrony’, as each brain area is

involved in performing individual tasks. However,

induction of anaesthesia induces strong

unidirectional interactions. This indicates that the

brain has now entered a ‘synchronised’ state, with

frontal and midline areas in the focus. This is in

agreement with observations that anaesthetic drug

administration causes frontal predominance by

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

192

increasing frontal cortical activity (Jameson and

Sloan, 2006).

Cortical sensory integration is considered as a

common mechanism of anaesthetic suppression of

conscious experience. It now seems more and more

likely that unconsciousness during anaesthesia is a

result of the brain’s inability to integrate information

(Hudetz, 2008, John and Prichep, 2005). One

possibility is that anaesthesia induces

unconsciousness through degradation of information

integration by disconnecting communication

between cortical networks. Another possibility is

that anaesthesia disrupts consciousness by putting

cortical networks in a synchronised state such that

they are no longer able to integrate incoming

information. Indeed, anaesthesia and other

consciousness-depressing mechanisms are

associated with increased cortical synchrony

(Rampil, 1998). Our observations here suggest that

Granger causality has indeed managed to capture

this shift of the brain activity to a more synchronised

state, and with decreased communication from

posterior to all other areas. Thus, Granger causality

can capture the physiological changes in the EEG

activity, which are associated with administration of

anaesthetic agents.

This work raises some additional considerations.

Firstly, an interesting observation is that the strength

of interaction appears to decrease towards baseline

some minutes after induction of anaesthesia for

interactions between the left frontal areas and other

areas, whereas the strength of interaction remains at

the same level for interactions between the right

frontal and other areas. It would be interesting to

observe longer periods after induction of anaesthesia

in order to investigate the role of each frontal

hemisphere in synchronisation during maintenance

of anaesthesia, whether this is disrupted by strong

stimuli, such as tracheal intubation, and whether the

same patterns of interactions are observed again at

the end point of anaesthesia, but in the reverse

direction. Secondly, the effect of neuromuscular

blocking agents on the EEG is still not fully

understood. Thus, it would be useful to investigate

whether the observed patterns of interaction are

similar when neuromuscular blocking agents are not

administered. Thirdly, analysis with increased

spatial resolution would allow us to identify a more

exact location of the areas that are acting as

synchronisation pacemakers. For this, Granger

causality should be estimated for smaller electrode

grids, and even for individual electrodes. However,

these are beyond the scope of this work and remain

the subject for future investigations.

Taking these additional considerations in mind,

if changes in the bidirectional interactions identified

by Granger causality could be expressed in the form

of a single number from 0-100, then it might be

possible in the future to utilise this measure to alert

the anaesthetist in cases of impending awareness

during surgery.

4 CONCLUSIONS

We have shown that Granger causality can be used

to extract information reflecting the physiological

interactions between different brain areas during

induction of general anaesthesia. A measure that can

extract the deeper interactions within the brain

through the observed EEG activity would be useful

not only for studying the physiological mechanisms

of anaesthesia, but also in a monitor of anaesthetic

depth to provide objective assessment of the state of

hypnosis of the patient.

ACKNOWLEDGEMENTS

The authors would like to thank the staff at Nicosia

General Hospital and the anonymous volunteers.

This work is part of the Cyprus Research Promotion

Foundation’s Framework Programme for Research,

Technological Development and Innovation 2008

(DESMI 2008), co-funded by the Republic of

Cyprus and the European Regional Development

Fund.

REFERENCES

Barr, G., Jakobsson, J. G., Owall, A. & Anderson, R. E.

(1999) Nitrous oxide does not alter bispectral index:

study with nitrous oxide as sole agent and as an

adjunct to i.v. anaesthesia. British Journal of

Anaesthesia, 82, 827-830.

Bennett, C., Voss, L. J., Barnard, J. P. M. & Sleigh, J. W.

(2009) Practical use of the raw electroencephalogram

waveform during general anesthesia: the art and

science. Neurosurgical Anesthesiology and

Neuroscience, 109, 539-550.

Dahaba, A. A. (2005) Different Conditions That Could

Result in the Bispectral Index Indicating an Incorrect

Hypnotic State. Anesth Analg, 101, 765-773.

Granger, C. W. J. (1969) Investigating causal relations by

econometric models and cross-spectral methods.

Econometrica, 37, 424-438.

USING GRANGER CAUSALITY TO CHARACTERISE BIDIRECTIONAL INTERACTIONS IN THE HUMAN

BRAIN DURING INDUCTION OF ANAESTHESIA

193

Hammeroff, S. R. (2006) The entwined mysteries of

anaesthesia and consciousness. Anesthesiology, 105,

400-412.

Hudetz, A. G. (2008) Are we unconscious during general

anesthesia? Intl Anesth Clinics, 46, 25-42.

Jameson, L. C. & Sloan, T. B. (2006) Using EEG to

monitor anesthesia drug effects during surgery. J. of

Clinical Monitoring and Computing, 20, 445-472.

John, E. R. & Prichep, L. S. (2005) The Anesthetic

Cascade: A Theory of How Anesthesia Suppresses

Consciousness. Anesthesiology, 102, 447-471.

Messner, M., Beese, U., Romstock, J. & AL., E. (2003)

The bispectral index declines during neuromuscular

block in fully awake persons. Anesth Analg, 97, 488-

491.

Mychaskiw, G., Horowitz, M., Sachdev, V. & Heath, B. J.

(2001) Explicit intraoperative recall at a Bispectral

index of 47. Anesth Analg, 92, 808-809.

Myles, P. S., Symons, J. A. & Leslie, K. (2003)

Anaesthetists' attitudes towards awareness and depth-

of-anaesthesia monitoring. Anaesthesia, 58, 11-16.

Pereda, E., Quian-Quiroga, R. & Bhattacharya, J. (2005)

Nonlinear multivariate analysis of neurophysiological

signals. Progress in Neurobiology, 77, 1-37.

Rampersad, S. E. & Mulroy, M. F. (2005) A case of

awareness despite an "adequate depth of anaesthesia"

as indicated by a Bispectral Index monitor. Anesth

Analg, 100, 1363-1364.

Rampil, I. J. (1998) A primer for EEG signal processing in

anesthesia. Anesthesiology, 89, 980-1002.

Ranta, S. (2002) Awareness with recall during general

anesthesia. Dept of Anaesthesia and Intensive Care

Medicine. Helsinki, University of Helsinki, Finland.

Russell, I. F. (2006) The Narcotrend "depth of

anaesthesia" monitor cannot reliably detect

consciousness during general anaesthesia: an

investigation using the isolated forearm technique.

British Journal of Anaesthesia, 96, 346-352.

Sigl, J. C. & Chamoun, N. G. (1994) An introduction to

bispectral analysis of the electroencephalogram.

Journal of Clinical Monitoring and Computing, 10,

392-404.

Sleigh, J. W., Andrzejowski, J., Steyn-Ross, A. & Steyn-

Ross, M. (1999) The Bispectral Index: a measure of

depth of sleep? Anesth Analg, 88, 659-661.

Tseng, S.-Y., Chen, R.-C., Chong, F.-C. & KUO, T.-S.

(1995) Evaluation of parametric methods in EEG

signal analysis. Med Eng Phys, 17, 71-78.

Vaz, F., De Oliveira, P. G. & Principe, J. C. (1987) A

study on the best order for Autoregressive EEG

modelling. Int. J. Bio-Medical Computing, 20, 41-50.

Viertiö-Oja, H., Maja, V., Särkelä, M., Talja, P.,

Tenkanen, N., Tolvanen-Laakso, H., Paloheimo, M.,

Vakkuri, A., Yli-Hankala, A. & Meriläinen, P. (2004)

Description of the Entropy Algorithm as applied in the

Datex-Ohmeda S/5 Entropy Module. Acta

Anaesthesiol Scand, 48, 154-161.

Voss, L. J. & Sleigh, J. W. (2007) Monitoring

consciousness: the current status of EEG-based depth

of anaesthesia monitors. Best Practice & Research

Clinical Anaesthesiology, 21, 313-325.

Wiener, N. (1956) The theory of prediction. In

Beckenbach, E. F. (Ed.) Modern Mathematics for

Engineers. New York, McGraw-Hill.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

194