CONTINUOUS PREFERENCES FOR ACTION SELECTION
Patricia Everaere
1
and Emmanuelle Grislin-Le Strugeon
2
1
Universit
´
e Lille 1, LIFL, UMR 8022, 59655 Villeneuve d´ Ascq, France
2
Univ. Lille Nord de France, UVHC, LAMIH-FRE 3304, F-59313 Valenciennes, France
Keywords:
Autonomous agent, Action selection, Vote, Preferences.
Abstract:
We have investigated the use of continuous alternatives for action selection by a behavior-oriented agent. Such
an agent is made of concurrent “behaviors”; each of these behaviors reacts to specific stimuli and provides
a response according to a low-level goal. Since the behaviors are specialized, they can provide concurrent
responses and conflicts among them must be solved to perform a coherent global behavior of the agent. In
this context, voting methods allow to select only one of the responses of the behaviors, while taking into
account their preferences and respecting all of their constraints. Previous works are based on action spaces
limited to few discrete values and have shown difficulties in determining the behaviors weights for the vote.
Furthermore, these works generally not allow to express the indifference of a behavior on a alternative’s
component, i.e. the fact that a behavior has no preference on the value of one component of an alternative.
We propose in this article a method to use continuous values for the alternatives and a fair vote based on
one alternative proposition per behavior. Our framework also allows the expression of indifference between
alternatives. This proposition has been tested and compared, and the results show that our approach is better
than previous propositions to avoid locked situations.
1 INTRODUCTION
Autonomous situated agents like simulated robots or
virtual characters have to adapt their behavior accord-
ing to the changes occurring in their environment.
One kind of behavior adaptation concerns the agent’s
short-term reaction to modifications of a dynamical
environment. In this context, the agent decides what
to do at the next step, in reaction to events or at regu-
lar time steps. The decision concerns which action to
perform, i.e. a set of command values to control the
actuators of a robot or the actions of a virtual charac-
ter.
The problem of selecting the most appropriate
action in the current situation, called the action se-
lection (AS) problem (Maes, 1989), can be solved
using different approaches. Our work belongs to
the behavior-based approach (Brooks, 1986; Mataric,
1992; Arkin, 1998), common in robotics and ap-
plied in various domains such as underwater vehicle
(Rosenblatt et al., 2002), virtual characters (Bryson
and Thorisson, 2000) and services (Antonelli et al.,
2008). According to the behavior-based approach, the
agent is made of a set of concurrent behavior mod-
ules, called “behaviors”; each of them reacts to spe-
cific stimuli and provides a response according to a
low-level goal. For example, one of a simulated mo-
bile robot’s behaviors can be dedicated to wall follow-
ing, and reacts according to the distance to the wall.
Since the behaviors are specialized, they can pro-
vide concurrent responses. As a consequence, it is
necessary to solve conflicts among the behaviors in
the aim to perform a coherent global behavior of the
agent. In a behavior-based agent, action selection is
thus a collective decision process. The problem is
to find a coordination process for the agent to make
a decision based on multiple, concurrent and eventu-
ally conflictual tendencies, generally within time con-
straints (see Fig. 1).
Numerous methods have been proposed to select
one of the actions proposed by the behaviors that
compose a behavior-based agent. Some of them arbi-
trate among the propositions of the behaviors, while
others make a fusion of these propositions. A third
way exists, that arbitrates in taking into account the
preferences of the behaviors: the voting-based meth-
54
Grislin-Le Strugeon E. and Everaere P..
CONTINUOUS PREFERENCES FOR ACTION SELECTION.
DOI: 10.5220/0003148800540063
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 54-63
ISBN: 978-989-8425-41-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

!"#$%&'()*
+++
!"#$%&'(),
-"."/0&',
-0&12.&
$/0&',
Figure 1: Behavior-based action selection.
ods (Rosenblatt, 1996; Hostetler and Karrney, 2002).
The work presented in this paper is based on the ac-
tion selection by a voting system to coordinate behav-
iors. We extend previous works by the study of two
points: (a) how the behaviors can express their indif-
ference towards some components of the action, and
(b) how the expression of the action values by contin-
uous values can contribute to avoid locked situations.
The rest of the paper is organized as follows. In
Section 2, our work is situated in the context of rele-
vant research. The action selection process is detailed
in Section 3, and we present our solution. We explain
how this proposition avoids some of the recurrent dif-
ficulties in using a voting system to coordinate the be-
haviors. The tests and results are described in Section
4, before discussion (Section 5) and conclusion.
2 RELATED WORKS
This study is based on previous works in the domain
of behavior-based architectures and methods. We fo-
cus more specifically on the action selection problem,
i.e. the problem of selecting the most appropriate
action in the current situation (Maes, 1989). In the
context of behavior-based agents, the action selection
methods are usually classified in two main categories
(Pirjanian, 1999): arbitration and fusion.
In the arbitration or competition category, the
principle is to select one of the behaviors to which the
control is delegated until the next step. The methods
based on priorities (Brooks, 1986; Mataric, 1992), fi-
nite state machines (Bryson, 2002) and activation net-
works (Maes, 1989; Dorer, 1999) belong to the arbi-
tration category.
In the fusion or cooperation category, the principle
is to integrate all of the behaviors’ responses into the
resulting action. The methods based on linear combi-
nation (Reynolds, 1999), potential fields (Rosenblatt,
1996), schemas (Arkin, 1998), fuzzy behavior control
(Tunstel, 1995; Pirjanian and Mataric, 1999) and GA
(Flacher and Sigaud, 2003) belong to the fusion cate-
gory.
The arbitration category is based on a dictatorial
approach because the decision is made by one behav-
ior. This may have two consequences: the violation of
the other behaviors’ constraints and an eventual oscil-
lation of the system if different behaviors make alter-
natively the decision. The fusion category is based on
a more democratic approach than the previous one,
but it can produce results that are not satisfying for
any of the behaviors.
These specific characteristics of each category can
be solved in dynamically switching from a method
to another like in the APOC system (Scheutz and
Andronache, 2004). We have studied another so-
lution, more democratic and fair: the use of a vot-
ing method (Rosenblatt, 1996; Hostetler and Karrney,
2002; Hanon et al., 2005). With this approach, one
of the proposed responses is selected by a process
which integrates the behaviors’ preferences and con-
straints. This allows to respect these preferences and
constraints while avoiding a fusion of the actions that
are proposed. In this process, the behaviors propose
a set of alternatives (propositions of values for the ac-
tion) and they express their preferences among all the
available alternatives. Then, the selected alternative is
chosen, as the best alternative after aggregation of the
behaviors’ preferences.
However, in the existing AS voting systems, the
set of alternatives is generally restricted to a very lim-
ited action space, due to complexity reasons or ap-
plication dependent constraints. Another difficulty
comes from the parameterization of the model due
to the use of weights on the behaviors’ vote. This
is solved by learning mechanisms (Maes and Brooks,
1990) but the calculated weights are very specialized
to a certain environment, and would not be adapted
to other context. Concerning the expression of the
indifference of the behaviors towards some compo-
nents of the action, a first proposition has been made
in (Hanon et al., 2005) to complete the alternatives be-
fore the vote, but the complexity of the treatment en-
tails some difficulties to maintain the time constraint.
In this paper, we give a new solution to the prob-
lem of action selection. Objectives are both:
• use of a coordination function, which takes into
account fairly all the behaviors (in a positive way
for the wishes, in a negative way for the con-
straints) and contributes to avoid (dead- or live-)
locked situations,
• diminution of the algorithm complexity, in order
to keep the reactivity of the system.
CONTINUOUS PREFERENCES FOR ACTION SELECTION
55

3 ACTION SELECTION
The aim of the action selection process is to choose
the next step action to perform. Action is a generic
term that recovers distinct realities depending on the
type of agent and its environment. For instance, con-
cerning a robot, an action is the set of the actuators
commands while for a software agent, an action is the
set of its output values. In both cases, the action can
be composed of several elementary actions: an action
A is a n-uplet A = (a
1
,...,a
n
), where each action a
i
has its value in a domain D
i
. The set of the possible
values for A is thus D
1
× ... × D
n
. For example, in
the autonomous navigation, n = 2 with A = {velocity,
orientation}. According to the technical constraints
specific to a certain application, we can have D
1
=
[−50,50] (speed units) and D
2
= [0;360](degrees).
The elementary actions may not be independent:
often, the value given to an elementary action a
i
can
influence the values given to other a
j
. And this de-
pendency may be different for the behaviors. In the
precedent example, the behavior “obstacle avoiding”
concerns the two elementary actions since the agent
position depends both on its velocity and its orienta-
tion. As a consequence, the values of the elementary
actions can generally not be selected separately: the
decision is made at once on all the elementary actions,
as a ”whole” action and not on independent parts of
it.
A behavior-based structure is composed of a set
of distributed independent behaviors B = (b
1
,...,b
p
)
and a centralized coordination system. Each behavior
is concerned by a the subset of the stimuli, and re-
acts according to its specific (generally low-level) ob-
jectives, e.g. goal seeking, obstacle avoidance, wall-
following, etc. Each behavior proposes action val-
uations to reach its goals. A proposition made by
the behavior b
i
is an alternative A
b
i
= (a
b
i
1
,...,a
b
i
n
)
∈ D
1
× ... × D
n
. For example, the “goal seeking” be-
havior can propose the alternative A = (2,30) with its
preferred values for the action: a value of 2 for the
speed units and a heading of 30 degrees.
With a preference aggregation process like a vot-
ing system, the action selection by the behaviors is
performed in four phases (see Algorithm 1):
1. proposition of the alternatives
2. constraints application
3. preferences elicitation
4. selection of one of the alternatives as the best
choice.
The following subsections describe these four
phases, their specific difficulties and the solutions we
Algorithm 1. Action selection by voting behaviors.
behavior set B = {b
1
,...,b
n
}
alternative list l =
/
0
// 1. proposition of the alternatives
for all behavior b
i
∈ B do
add p alternatives to alternative list l
end for
// 2. constraints application
for all behavior b
i
∈ B do
for all alternative A
j
∈ l do
A
0
j
← application of b
i
constraints to A
j
end for
l ← (l \ {A
j
}) ∪ {A
0
j
}
end for
// 3. preferences elicitation
for all behavior b
i
∈ B do
b
i
sorts alternatives ∈ l
end for
// 4. selection of one action
selected alternative ← winner of the preferences
aggregation
return the selected action
propose. More particularly, we will discuss the in-
fluence of two parameters on the result of the vote:
the use of discrete or continuous alternatives and the
number of alternatives.
3.1 Alternatives
The choices made in Algorithm 1 have a lot of conse-
quences and have to be discussed. We have stressed
three limitations: the obligation to choose exact dis-
crete value for actions; the possibility for a behavior
to give one, two, or any number of alternatives; and fi-
nally the difficulty of taking into account indifference.
3.1.1 Action Space
A difficulty comes from the size of the action space
because the set of all combinations D
1
× ... × D
n
can
be very large. The behaviors can not give their prefer-
ences in an extensive way. In our example, the action
space of the orientation is a subset of R.
This difficulty is avoided in most existing works
by reducing the action space to few discrete values,
even when the action space is initially a continuous
domain. This allows to enumerate the values of the
elementary action combination set, these values form
the set of alternatives. This is reasonable when these
values are strongly linked to actuators, like the seven
motor commands , ”hard left” ”left”, ”soft left”, ”for-
ward”, ..., to ”hard right” in (Kwong et al., 2002).
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
56

This is less understandable when these values are in-
tended to command flexible actions, like the naviga-
tion of a virtual character in (Hostetler and Karrney,
2002). For example, a behavior which objective is
to accelerate would be satisfied by any speed value
greater than the current one. With s being the cur-
rent value of the speed, the previous objective can be
expressed by discrete values, e.g. the proposition of
(s+∆) or several values {(s+∆
1
);(s+∆
2
);(s+∆
3
)},
or by the continuous set ]s;∞[.
Does the choice of using discrete or continuous
values have any influence on the results of the action
selection? Our hypothesis is that some locked situa-
tion could be avoided in using continuous values in-
stead of discrete values. For example, even if a be-
havior can not accept the value a
1
, nor the value a
2
,
it may accept some intermediate values in the inter-
val ]a
1
;a
2
[. We propose thus to express the alterna-
tives as intervals A
b
i
= ([a
11
;a
12
],...,[a
n1
;a
n2
]) with
[a
11
;a
12
] ⊆ D
1
,...,[a
n1
;a
n2
] ⊆ D
n
.
3.1.2 Number of Alternatives per behavior
A behavior that proposes more than one alternative
can influence the result of the vote in its favor. Let’s
take an example:
Three behaviors M
1
, M
2
and M
3
:
• M
1
proposes A = (1.5,4,8)
• M
2
proposes B = (3,2,3)
• M
3
proposes C = (5,6,7)
The votes are:
• M
1
votes A > B > C
• M
2
votes B > A > C
• M
3
votes C > B > A
The results are, using Inverse Borda Rule (1 points
for the first alternative, 2 for the second and 3 for the
third): 6 points for A, 5 for B and 7 for C. B is thus
the winner.
If M
1
proposes more than one alternative, it can
change the result:
• M
1
proposes A = (1.5,4,8), A
1
= (1,4,8) and
A
2
= (2,4,8)
• M
2
proposes B = (3,2,3)
• M
3
proposes C = (5,6,7)
and the votes are:
• M
1
votes A
2
> A
1
> A > B > C
• M
2
votes B > A
2
> A
1
> A > C
• M
3
votes C > B > A
2
> A
1
> A
The results are: 12 points for A, 9 points for A
1
, 6
points for A
2
, 7 for B and 11 for C. A
2
is the winner.
This example shows that the number of alternatives
proposed by a behavior may change the result of the
aggregating process (it is shown here with the Borda
rule, but similar examples can be constructed with any
other voting rule).
As a consequence, we propose to limit the alter-
natives to only one alternative per behavior (p = 1 in
the Algorithm 1). This limitation ensures a fair treat-
ment among all the concurrent behaviors. Further-
more, this can be combined with the use of contin-
uous values. Following the example above, M
1
may
propose A = ([1;2],4,8) if this alternative matches its
goals.
3.1.3 Indifference Handling
Behaviors can be indifferent to some of the elemen-
tary actions. For example, a behavior which objective
is only to reach a certain speed would be indifferent
to the value of the orientation. Expressing the indif-
ference towards the value of a
i
can be made in using a
specific value (like the ”Joker” value in (Hanon et al.,
2005)). This proposition is interesting and simple but
a difficulty is then to sort vectors of actions when
one or two values are lacking. Replacing value by a
joker symbol induces a problem of incomparability
between vectors of actions. An other solution to
express indifference consists in replacing the missing
value by the set of all the possible values, i.e. the D
i
domain. But in this case, one vector is transformed in
d
i
vectors, where d
i
is the cardinality of the domain
D
i
. This transformation is not compatible with the
limitation to one alternative for each behavior.
During the proposition phase, each behavior pro-
poses at most one alternative and this alternative can
include intervals of values. The result of this first
phase is thus a list of p alternatives l =
S
i
A
b
i
, with
A
b
i
= ([a
11
;a
12
],...,[a
n1
;a
n2
]). To express its indif-
ference towards the elementary action a
i
, a behavior
proposes the interval of all possible values, i.e. the
whole domain D
i
of a
i
. This value is then used as any
other component of the alternative.
3.2 Constraints Application
The knowledge of the constraints due to the environ-
ment or the context, e.g. the presence of an obstacle,
are distributed among the behaviors, just like the el-
ementary objectives of the agent are distributed. As
a consequence, each behavior can restrict the space
of the possible actions. In (Hostetler and Karrney,
2002)), a restriction is called a “veto” because each
CONTINUOUS PREFERENCES FOR ACTION SELECTION
57

of the behaviors can eliminate any of the alternatives
in the agenda.
When an action is composed of independent parts,
constraints can easily be expressed as restrictions on
the elementary actions domains. But in most cases,
the values of the elementary actions depend from each
other and the restrictions are functions that link these
values. For example, a constraint on heading and ve-
locity should express that ”heading h and speed s must
be chosen such as s ∗tan(h) < 10 units”. For this rea-
son, and since each behavior has its own objective, we
propose that each behavior applies its own constraints
to the alternatives list (see application of interval con-
straints on values in Table 1). The new agenda is the
smallest common resulting set of the constraint appli-
cation phase.
Table 1: Application of the restriction (v = [v1;v2]) to the
alternative component (a
i
= [a
i1
;a
i2
]).
Respective positions of
restriction and action values Resulting action Value
!
"
#
a
i
0
= a
i
!
"
#
!
"
#
a
i
0
= [a
i1
;v1]
!
"
#
a
i
0
= [v2;a
i2
]
!
"
#
a
i
0
=
/
0
!
"
#
a
i
0
= [a
i1
;v1] ∪ [v2;a
i2
]
As the alternatives are expressed by continuous values
in our proposition, a restriction can produce a “split-
ting” of the intervals (Cf. 4th case in Table 1). For
example, consider the alternative x = ([x
11
,x
12
],x
2
)
and the restriction v = [v
1
,v
2
] with [v
1
,v
2
] ⊂ [x
11
,x
12
].
The application of v to x leads to replace x by the two
alternatives ([x
11
,v
1
],x
2
) and ([v
2
,x
12
],x
2
).
At the end of this phase, the resulting agenda re-
spects all of the behaviors’ constraints.
3.3 Preference Elicitation
The agenda is proposed to the behaviors, and each
behavior produces a classification among the avail-
able alternatives according to its preferences. Each
behavior has its own utility function. The compari-
son between the alternatives can be based on different
criteria according to the behavior, since the behavior’s
goals are distinct. The comparison can be made on the
values of all or only parts of the decision components
in case of indifference toward some of them.
The use of continuous alternatives may cause
some difficulties in the expression of their preferences
by the behaviors, which is more difficult with contin-
uous data than with discrete data.
In the preference elicitation phase, the difficulty
is, for each behavior, to classify the interval alterna-
tives. With the assumption that a behavior has de-
fined its preferred action values as intervals, how can
it compare these values to the alternatives?
One first solution is to approximate an interval by
its median value. This strongly reduces the problem
to a comparison of discrete values. But we lose the
richness brought by the use of continuous values. An-
other solution is to find similarity metrics that can
be used to compare the alternatives. The Hausdorff
distance and dissemblance index are two functions of
primary distances that are used to build compatibility
measures (Cross and Sudkamp, 2002).
The Hausdorff distance q measures the distance
between two compact subsets of the real numbers X
et Y :
q(X,Y ) = max(σ(X,Y ), σ(Y,X))
with
σ(X,Y ) = sup
x∈X
in f
y∈Y
d
2
(x,y)
where d
2
is the euclidian distance between real
numbers. Informally, the value of q(X,Y ) represents
the maximal distance between any element of the set
X to the set Y .
The distance between two intervals of reals V =
[v
1
,v
2
] and W = [w
1
,w
2
] with this measure is given
by:
q(V,W ) = max(| v
1
− w
1
|,| v
2
− w
2
|)
The measure of dissimilarity between two inter-
vals of real numbers V and W is calculated by:
D(V,W ) =
| v
1
− w
1
| + | v
2
− w
2
|
2(β
2
− β
1
)
where the interval [β
1
,β
2
] includes V and W . Divid-
ing by 2(β
2
− β
1
) results in a normalized measure
0 ≤ D(V,W ) ≤ 1. For example, if V = [6,7] and
W = [9,11], one possibility for [β
1
,β
2
] is to select
[6,11]. With this choice, the dissimilarity between V
and W is equal to (9 − 6) + (11 − 7)/2.5 = 7/10.
The measure of dissimilarity is maximal and equal
to 1 if V = [β
1
,β
1
] and W = [β
2
,β
2
]. This max-
imal value can be obtained in very different cases,
for example when we have ([10,10],[20,20]) and
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
58

([10,10],[1000,1000]). To differentiate these cases,
we can add another measure, e.g. the interval length.
3.4 Preference Aggregation
From the set of all the propositions of values by
the behaviors, the decision process must provide one
value for each action A.
Many voting systems can be used in this phase. In
our context, the chosen voting system must be well-
adapted to un-weighted vote and determine a win-
ner as fast as possible. We choose a scoring voting
method because this method satisfies reinforcement
and participation (see (Moulin, 1988)). More pre-
cisely, we use Inverse Borda Rule: 1 point is given to
the best alternative, 2 points to the second, and so on.
Then, a sum is made and the winner is the alternative
with the least score (in case of ex-aequo, the winner
is chosen randomly). This rule is “effectiveness” for
Weber (Weber, 1978), the expected satisfaction of be-
haviors if the utilities associated with the alternatives
are independently and uniformly distributed is opti-
mal with this rule.
Once an alternative is chosen, we obtain intervals
for the action values. A difficulty is then to determine
the value to affect to the action at the next step: a
transformation has to be realized because the action
command must be a discrete value. Different solu-
tions are possible to replace the winner interval by one
of its values: the median, or a randomly chosen value,
or chosen using an heuristic, etc. This transformation
may also take into account the actual value of the sys-
tem, depending on wether the actual value belongs to
the winner interval or not.
While explaining the four phases of the action se-
lection by voting behaviors, we have made the hy-
pothesis that the use of continuous values in the alter-
natives enables to avoid some locked situations and
to express the indifference toward some action values.
To confirm this, we made experiments on a virtual au-
tonomous agent.
4 EXPERIMENTS
The aim of the experiments is to compare different
methods of action selection based on voting. Our hy-
pothesis is that the use of continuous alternatives can
prevent locked situations in which the agent does not
find any solution.
The application context is a simulated environ-
ment with obstacles and moving agents. Important
simplifications have been made in comparison to a
real robotic navigation context: for example, no lim-
itation is made on the velocity or the rotation of the
agent.
In this context, the action includes n = 2 compo-
nents, with the speed x
1
∈ D
1
= [0;3] and the heading
x
2
∈ D
2
= [0;360].
4.1 Behaviors
The agent includes three permanent behaviors –
GoFast, TowardGoal, Inertia– and one behavior –
AvoidObstacles– that is activated according to the
perceived environment:
• the behavior “GoFast” tends to reach a wished
speed; it is indifferent to the heading. It proposes
one alternative that expresses the will to go faster
whatever the heading is.
• the behavior “TowardGoal” tends to orientates to-
ward the goal on the base of the current speed.
• the behavior “Inertia” is used to regulates the
moving in avoiding unuseful changes from one
step to the next one.
• the behavior “avoidObstacle” is dynamically ac-
tivated according to the perceived environment:
one “avoidObstacle” behavior is created for each
perceived obstacle. Each behavior of this type
proposes an alternative on the base of the current
speed as the maximal wished speed and a heading
that avoids the obstacle.
4.2 Methods
The action selection phases are those described in
Algorithm 1. We have tested 6 methods that use
behavior- and voting-based action selection. These
methods have common features:
• the behaviors propose alternatives;
• the behaviors can express their constraints in par-
tially or completely eliminating some of the alter-
natives;
• the behaviors express their preferences in ordering
the alternatives; the order is non-strict (there can
be ex-aequo) and complete (all is ordered);
• the preferences are aggregated using an Inverse
Borda politics.
We have tested different methods based on the fol-
lowing choices:
• discrete or continuous values
• indifference for an action component can be ex-
pressed or not
CONTINUOUS PREFERENCES FOR ACTION SELECTION
59

• for the continuous values, the alternatives can be
changed into discrete values before the vote or not
Numerous techniques can be used to change the
continuous values of the action into discrete ones:
mean, median, randomization, heuristics,... We have
chosen to study the use of median and randomization
techniques.
The methods we have tested are summed up in Ta-
ble 2):
• The three first methods use alternatives with dis-
crete values. Two methods do not allow to express
the indifference toward one of the action compo-
nent value, which is thus replaced by its current
value: in Method no indiff. 1, each behavior pro-
poses one and only one alternative; in Method no
indiff. 2, the “avoidObstacle” behavior proposes
two alternatives, i.e. one for each bound of the
obstacle. In the third method, Method product,
the behaviors can express indifference toward one
of the action in using a ”Joker” value. The alter-
natives that include Joker values are completed by
the values proposed in the other alternatives.
• The three last methods use alternatives with con-
tinuous values, i.e. the values can be express as
intervals. In Method median before vote, the in-
tervals are changed into their median values be-
fore the vote. In the two other methods, the vote
is made on the intervals. The behaviors must be
able to express their preferences in sorting inter-
vals. We use the dissemblance function for the
comparison of the intervals. The result is an inter-
val that must be changed into a discrete value for
the action to be performed: in Method median
after vote, the winner interval is changed into its
median value; in Method one of result, one of
the values is randomly chosen in the winner inter-
val. In this last method, we have chosen to favour
the current value in the aim to have a globally
“smoother” behavior: random is a normal distri-
bution that is centered on the current value when
this one belongs to the winner interval. When the
alternatives are made of intervals, the application
of the restrictions consists in ”crossing” the alter-
native intervals and the restriction intervals (see
Table 1). This operation can divide the alterna-
tives into subsets as mentioned in Part 3.2.
4.3 Environment
For the experiments, we used the NetLogo (Wilensky,
1999) environment, that offers the possibility to use
continuous spaces for the agent’s position (continu-
ous x and y coordinates). The state of the model is set
up at each simulated time step. Independently of the
simulated time count, the real duration of the run can
be measured. This measure is not meaningful regard-
ing its absolute value (depending on parameters like
the processor frequency), but we use it to compare the
methods.
In the following experiments, the agent must reach
a target within a given number of simulation steps
while avoiding obstacles. At each simulation step, the
agent perceives its environment in a 2 units radius cir-
cle, and then selects a speed and a heading to move.
When it does not find any solution or when its solution
is wrong because the action would make it occupy a
non idle place, the agent is stopped during one step
or more; we call it a ”locking situation”. The envi-
ronment changes dynamically, according to a param-
eter that determines the rate of obstacles that change
between two simulation steps. In fact, the environ-
ment changes, then there is a stable step during which
the agent moves, and then the environment changes
again.
The environment is simulated by a 21x21 patches
grid, with 20 pixels per patch. The obstacles occupy
the environment at the constant rate of 25% of the grid
cells, but their places vary according to the change
rate: from 5% to 25% of the obstacles places that
change at each step (see the example given in Fig.
2). The results are the average values given by 200
runs on each configuration, i.e. one method with one
change rate.
Figure 2: Example of two successive environmental situa-
tions with a change of 25% of the obstacles. In green: the
obstacles, in white: free spaces, in black: the target.
4.4 Results
We have evaluated the selection methods with an in-
creasing change rate in the environment. In each en-
vironment, we have measured:
• the time taken by the agent to make its decision
about the action selection;
• the success rate in reaching the target within a lim-
ited amount of steps;
• the number of steps in which the agent is stopped
(called ”locked steps”).
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
60

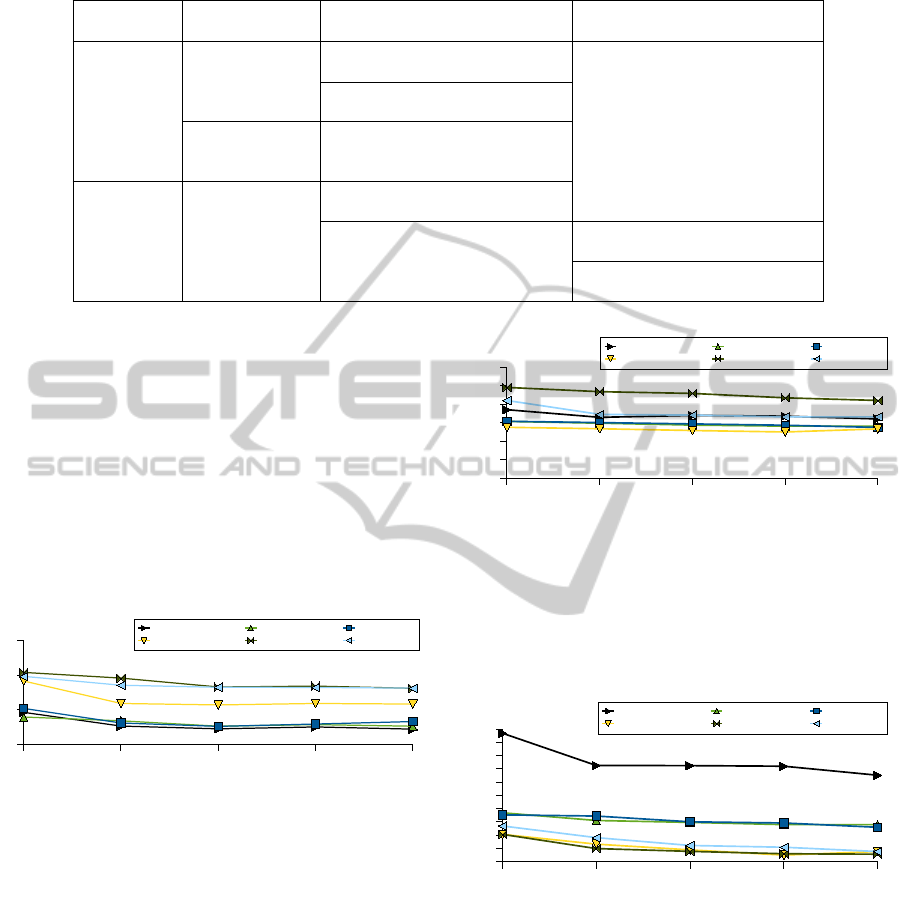
Table 2: The experimented methods (method name in bold text).
Alternative
type
Indifference Before vote After vote
Discrete
values
no
1 alternative / behavior
(no indiff. 1)
discrete resultsn alternatives / behavior
(no indiff. 2)
specific
discrete value
(Joker)
Joker replaced using cartesian
product with the other
alternatives (product)
Continuous
values
Value
domains
interval replaced by their
median (median before vote)
interval alternatives
winner interval replaced by its
median (median after vote)
winner interval replace by one
of its value (one of result)
The average time required by the decision making
does not vary a lot according to the change rate (cf.
Fig. 3). Methods using discrete values are faster than
methods using continuous values, the method Me-
dian before vote that converts the continuous values
into discrete values before the vote being situated in
the middle between the two types of methods. These
results are easy to understand as the voting process
requires to compare alternatives, and this task is more
complex with continuous values than with discrete
values.
!"#$%!"&'()$)&
*$+",-
. -/ -. 0/ 0.
/
-
0
1
23,4254667,- 23,4254667,0 %835'#)
9"54$2,:"638",;3)" 9"54$2,$6)"8,;3)" 32",36,8"&'()
#<$2+"&,=,&)"%,>?@
5"#4&432,)49"
>9&@
Figure 3: Mean decision time.
The total number of steps remains almost constant
even with the increase of the number of changes per
step (cf. Fig. 4). In our tests, all of the methods ex-
cept one require between 30 and 40 steps to reach the
target. One method needs more steps than the others:
the Median after vote method. From our analysis
of the results, it seems that choosing the median of
the resulting interval causes to strengthen the avoid-
ing behaviors, as if the agent turns back to avoid col-
lision, and thus, requires a higher amount of steps be-
fore reaching the target.
About the locked steps (cf. Fig. 5), the results
show that methods using continuous values cause less
locking situations than the methods using discrete val-
ues. The disadvantage is even worst for the method
No indiff. 1 that proposes only one alternative per
!"#$%!"&'()$)&
*$+",-
. -/ -. 0/ 0.
/
-
0
1
2
.
3
4
5
6
-/
78,97:9;;<,- 78,97:9;;<,0 %=8:'#)
>":9$7,?";8=",@8)" >":9$7,$;)"=,@8)" 87",8;,= "&'()
#A$7+"&,B,&)"%,CDE
(8#F":,&)"%&,CDE
. -/ -. 0/ 0.
/
-/
0/
1/
2/
./
3/
78,97:9;;<,- 78,97:9;;<,0 %=8:'#)
>":9$7,?";8=",@8)" >":9$7,$;)"=,@8)" 87",8;,= "&'()
#A$7+"&,B,&)"%,CDE
G,&)"%&
Figure 4: Mean number of steps required to reach the target.
behavior, eliminating thus potential solutions. The
general tendency of all curves to decrease is due to
unlocking when an obstacle disappears with a change
in the environment.
!"#$%!"&'()$)&
*$+",-
. -/ -. 0/ 0.
/
-
0
1
2
.
3
4
5
6
-/
78,97:9;;<,- 78,97:9;;<,0 %=8:'#)
>":9$7,?";8=",@8)" >":9$7,$;)"=,@8)" 87",8;,="&'()
#A$7+"&,B,&)"%,CDE
(8#F":,&)"%&,CDE
. -/ -. 0/ 0.
/
/<0
/<2
/<3
/<5
-
78,97:9;;<,- 78,97:9;;<,0 %=8:'#)
>":9$7,?";8=",@8)" >":9$7,$;)"=,@8)" 87",8;,="&'()
#A$7+"&,B,&)"%,CDE
&'##"&&,CDE
. -/ -. 0/ 0.
/
-
0
1
2
.
3
4
5
6
-/
78,97:9;;<,- 78,97:9;;<,0 %=8:'#)
>":9$7,?";8=",@8)" >":9$7,$;)"=,@8)" 87",8;,="&'()
#A$7+"&,B,&)"%,CDE
(8#F":,&)"%&,CDE
Figure 5: Mean number of locked steps (% of the number
of steps required to reach the target.)
5 DISCUSSION
In this article, we have made a proposition using in-
tervals like in fuzzy control systems (Tunstel, 1995;
Selekwa et al., 2008). The difference is that the result
is not produced by a combination of the fuzzy func-
tions, but by an arbitration among the sets proposed
by the behaviors, i.e. the selected action is not issued
from a fusion operation: the selected action is not a
CONTINUOUS PREFERENCES FOR ACTION SELECTION
61

mixed solution that would risk to satisfy none of the
behaviors (Pirjanian and Mataric, 1999), but one of
the preferred alternatives.
Compared to the other methods based on the vote,
our objective has been to propose solutions to the lim-
itation of the action space and to the weighting prob-
lem (Hostetler and Karrney, 2002; Rosenblatt et al.,
2002). Compared to (Hanon et al., 2005), the contin-
uous values constitute another solution to the indiffer-
ence expression; they allow to decrease the number of
locked steps, but the time taken to make a decision re-
mains high.
Indeed, continuous values comparison, what is re-
alized with the Hausdorff distance in our proposition,
is time consuming. This is certainly the main lim-
itation of the method proposed here. However, in
these first tests, the decision time remains stable ac-
cording to the amount of changes in the environment.
The method should thus be chosen conditioned to stay
under the threshold value determined by the applica-
tion context, e.g. 50 MHz for screen refreshment in
a video game. More generally, the use of continuous
values seems to be relevant when the application con-
text presents three characteristics: the environment is
dynamical, the agent can perform actions that really
belong to continuous domains and the supplement of
time taken to manage the continuous values is accept-
able considering the application constraints.
These results have to be confirmed by comple-
mentary experiments in more complex environments
and situations, and with a higher number of action
components. Additional tests must be done too, in
the aim to compare the proposed method with other
different (non voting based) AS methods.
6 CONCLUSIONS
We have proposed an action selection method for
behavior-based agents that uses continuous values for
the alternatives, allows a fair vote based on one alter-
native proposition per behavior and the expression of
the indifference.
Different versions of the method have been tested
on a small dynamical environment. The results
show that the use of continuous values enables to
avoid some locking situations. Such methods are
more time-consuming than methods processing dis-
crete values, but the difference remains stable even
with an increasing change rate in the environment.
These characteristics must be confirmed by new ex-
periments in larger and various environments, and
with several agents.
The methods discussed here can be integrated in
a lot of different contexts. For example, they could
be used at the reactive low level of a multi-level
agent, composed of other, more cognitive and higher
level competences, such as in (Bryson and Thorisson,
2000). Another idea is to use this action selection pro-
cess to coordinate inter-agent actions, at the macro-
level of a multi-agent system, instead of the internal
behaviors of an agent, at a micro-level. Another in-
teresting perspective is to study these methods associ-
ated with learning mechanisms.
ACKNOWLEDGEMENTS
The authors wish to thank the CISIT, the Nord-Pas
de Calais regional authorities and the FEDER which
contributed to support this research. The authors
gratefully acknowledge the support of these institu-
tions. The authors thank also the anonymous review-
ers for their helpful remarks.
REFERENCES
Antonelli, G., Arrichiello, F., and Chiaverini, S. (2008). The
null-space-based behavioral control for autonomous
robotic systems. Intelligent Service Robotics, 1(1):27–
39.
Arkin, H. (1998). Behavior-based robotics. The MIT Press,
Cambridge.
Brooks, R. (1986). A robust layered control system for a
mobile robot. IEEE Journal of Robotics and Automa-
tion, RA-2:14–23.
Bryson, J. (2002). The behavior-oriented design of modular
agent intelligence. In Int. Workshop on Agent Technol-
ogy and Software Engineering (AgeS).
Bryson, J. and Thorisson, K. R. (2000). Dragons, bats
and evil knights: A three-layer design approach to
character-based creative play. VirtuaI Reality, 5:57–
71.
Cross, V. V. and Sudkamp, T. A. (2002). Similarity and
compatibility in fuzzy set theory: assessment and ap-
plications. Physica-Verlag GmbH, Heidelberg, Ger-
many, Germany.
Dorer, K. (1999). Behavior networks for continuous do-
mains using situation-dependent motivations. In Proc.
16th Int. Joint Conf. on Artificial Intelligence (IJCAI),
pages 1233–1238. Morgan Kaufmann.
Flacher, F. and Sigaud, O. (2003). Coordination spatiale
´
emergente par champs de potentiel. RSTI - TSI, Vie
artificielle(22):171–195.
Hanon, D., Grislin–Le Strugeon, E., and Mandiau, R.
(2005). A behaviour based decisional model us-
ing vote. In Mohammadian, M., editor, Proceedings
IAWTIC’2005 International Conference on Intelligent
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
62

Agents, Web Technologies and Internet Commerce,
ISBN 1740-88247-4.
Hostetler, T. and Karrney, J. (2002). Strolling down the av-
enue with a few close friends. In Eurographics Ireland
2002 Workshop Proceedings, pages 7–14, Dublin, Ire-
land.
Kwong, T. C., Shamsudin, H. A., Rosbi, M., and Jozsef,
K. T. (2002). Using voting technique in mobile robot
behavior coordination for goal-directed navigation.
Jurnal Teknologi, 36(D):55–70.
Maes, P. (1989). The dynamics of action selection. In Pro-
ceedings of the International Joint Conference on Ar-
tificial Intelligence-IJCAI’89. Morgan Kaufmann, De-
troit.
Maes, P. and Brooks, R. (1990). Learning to coordinate
behaviors. In AAAI, pages 796–802, Boston, MA.
Mataric, M. (1992). Behavior-based control: Main prop-
erties and implications. In Proceedings IEEE Interna-
tional Conference on Robotics and Automation, Work-
shop on Architectures for Intelligent Control Systems,
pages 46–54.
Moulin, H. (1988). Axioms of cooperative decision making.
Econometric society monographs. Cambridge Univer-
sity Press.
Pirjanian, P. (1999). Behaviour coordination mechanisms
- state-of-the-art. Research report, Robotics Research
Laboratory, University of Southern California.
Pirjanian, P. and Mataric, M. (1999). Multiple objec-
tive vs. fuzzy behavior coordination. In Lecture
Notes in Computer Science on Fuzzy Logic Techniques
for Autonomous Vehicle Navigation, pages 235–253.
Springer-Verlag.
Reynolds, C. (1999). Steering behaviors for autonomous
characters. In Game Developers Conference.
Rosenblatt, J. (1996). DAMN: A Distributed Architecture
for Mobile Navigation. PhD thesis, Carnegie Mellon
University, Pittsburgh, USA.
Rosenblatt, J., Williams, S., and Durrant-Whyte, H. (2002).
A behavior-based architecture for autonomous under-
water exploration. International Journal of Informa-
tion Sciences, 145(1):69–87.
Scheutz, M. and Andronache, V. (2004). Architectural
mechanisms for dynamic changes of behavior se-
lection strategies in behavior-based systems. IEEE
Transactions on Systems, Man, and Cybernetics, Part
B, 34(6):2377–2395.
Selekwa, M. F., Dunlap, D. D., Shi, D., and Jr., E. G. C.
(2008). Robot navigation in very cluttered environ-
ments by preference-based fuzzy behaviors. Robotics
and Autonomous Systems, 56(3):231–246.
Tunstel, E. (1995). Coordination of distributed fuzzy be-
haviors in mobile robot control. In IEEE International
Conference on Systems, Man,and Cybernetics, pages
4009–4014.
Weber, R. (1978). Reproducing Voting Systems. Cowles
Foundation.
Wilensky, U. (1999). Netlogo. http://ccl.northwestern.edu/
netlogo/. Center for Connected Learning and
Computer-Based Modeling. Northwestern University.
Evanston, IL.
CONTINUOUS PREFERENCES FOR ACTION SELECTION
63