
AUTOMATIC STATE SPACE AGGREGATION
USING A DENSITY BASED TECHNIQUE
Steven Loscalzo
1,2
1
Department of Computer Science, Binghamton University, Binghamton, NY, U.S.A.
Robert Wright
2
2
Information Directorate, Air Force Research Lab, Rome, NY, U.S.A.
Keywords:
State space abstraction, Reinforcement learning.
Abstract:
Applying reinforcement learning techniques in continuous environments is challenging because there are in-
finitely many states to visit in order to learn an optimal policy. To make this situation tractable, abstractions
are often used to reduce the infinite state space down to a small and finite one. Some of the more powerful and
commonplace abstractions, tiling abstractions such as CMAC, work by aggregating many base states into a
single abstract state. Unfortunately, significant manual effort is often necessary in order to apply them to non-
trivial control problems. Here we develop an automatic state space aggregation algorithm, Maximum Density
Separation, which can produce a meaningful abstraction with minimal manual effort. This method leverages
the density of observations in the space to construct a partition and aggregate states in a dense region to the
same abstract state. We show that the abstractions produced by this method on two benchmark reinforcement
learning problems can outperform fixed tiling methods in terms of both the convergence rate of a learning
algorithm and the number of abstract states needed.
1 INTRODUCTION
For reinforcement learning algorithms, learning in
an environment with continuous valued features is a
challenging problem since the state space S will be in-
finite. The objective of a reinforcement learning (RL)
algorithm is to learn an optimal policy π
∗
which en-
codes each action to take to get from some start state
s
i
∈ S to a goal state s
g
∈ S while minimizing a utility
measure. RL algorithms learn π
∗
by repeatedly ex-
periencing states on the way to s
g
. The probability
of reaching the same state twice approaches zero for
problems with continuous features, therefore directly
applying reinforcement learning algorithms in contin-
uous domain problems is infeasible. State space ab-
straction is needed to transform the problem in some
way to reduce the effective size of S to make RL ap-
plicable.
There are many ways to achieve such an abstrac-
tion, and (Li et al., 2006) constructed a five tier cate-
gorization scheme for them depending on the “coarse-
ness” of the abstraction and what parts of the optimal
policy π
∗
get carried over from the original space to
the abstract one. For three levels of coarse-
ness (model-irrelevance, Q
π
-irrelevance, and Q
∗
-
irrelevance) they prove that an optimal policy found
in the abstract space S
′
will also result in an optimal
policy in the groundstate space S . The other two cate-
gories (a
∗
-irrelevance an π
∗
-irrelevance) do not share
this same guarantee, though in some ways are more
valuable because they can abstract down the size of
the state space to a much larger degree than the other
three methods.
One of these classes of abstractions, the a
∗
-
irrelevance abstraction, which aggregate two base
states together if they share the same optimal action,
is the focus of this paper. One of the most popu-
lar types of abstraction techniques, tiling, falls into
this category. Examples of common tile based ab-
stractions include CMAC (Miller et al., 1990), and U-
tile distinction (Mccallum, 1996; Uther and Veloso,
1998). These methods aggregate ranges of a continu-
ous state space to discrete abstract states, resulting in
a finite environment for an RL algorithm to learn in.
While tile based methods have been shown effective
in a number of situations, there are serious drawbacks
249
Loscalzo S. and Wright R..
AUTOMATIC STATE SPACE AGGREGATION USING A DENSITY BASED TECHNIQUE.
DOI: 10.5220/0003150202490256
In Proceedings of the 3rd International Conference on Agents and Artificial Intelligence (ICAART-2011), pages 249-256
ISBN: 978-989-8425-40-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
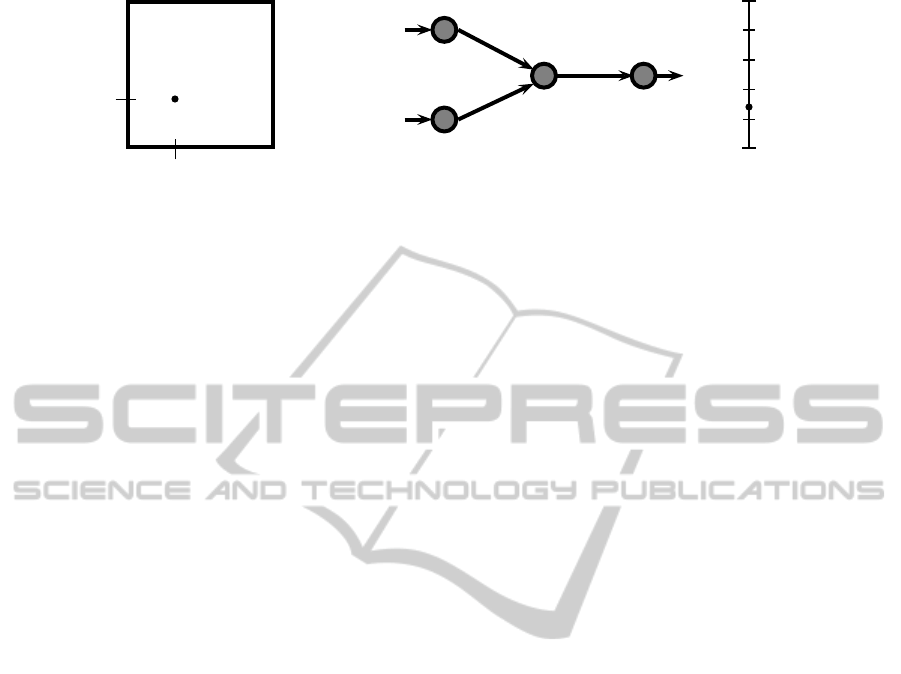
S
s
x
y
Perception X
Perception Y
s
x,y
Artificial Neural Network
x
y
z
S
′
s
′
1
s
′
2
s
′
3
s
′
4
s
′
5
z
0.0
1.0
Figure 1: Overview of the RL-SANE algorithm transforming a ground state s
x,y
in a sample two dimensional state space S to
the abstract state s
′
2
in the one dimensional abstract state space S
′
.
to using them (Sutton, 1996; Whiteson et al., 2007).
Engineering a tiling is typically done by hand, and
it can be very difficult to find an appropriate tiling
for a given problem or to correctly set the parame-
ters in methods that build a tiling during the learning
process. Automatic tiling methods (Whiteson et al.,
2007), that construct tilings during the learning pro-
cess, have shown to be very sensitive to parameter
choices. Recently, tiling methods have been shown
ineffective in the double pole balance setting, a chal-
lenging RL standard problem (Gomez et al., 2006).
Here we develop and evaluate an automatic aggre-
gation method called Maximum Density Separation
that efficiently learns how to abstract a state space but
still allows a learner to converge to the optimal pol-
icy. This abstraction is constructed on the one dimen-
sional state space produced by the RL-SANE algo-
rithm (Wright and Gemelli, 2009) which allows us to
focus on the aggregation technique and not on feature
space dimensionality reduction. This method lever-
ages the distribution of observations to choose intu-
itive abstract states in an effort to improve the speed
of learning. By using density patterns found in the ob-
servations we hope that useful abstractions can be dis-
covered without significant effort by the user. When
used in conjunction with feature space dimensional-
ity reduction techniques, automated state aggregation
methods will greatly increase the scalability and ap-
plicability of existing RL algorithms.
We show via empirical study on a mountain car
and double pole balance benchmark RL problems that
the Maximum Density Separation algorithm allows
the learning algorithm to significantly improve its rate
of convergence to π
∗
when compared to the base RL-
SANE algorithm using a fixed tiling and another more
simplistic automated approach based on random vari-
ations in the number of fixed tiles in the abstraction.
Additionally, we show that our automatic method is
capable of creating a more compact abstract space
than a traditional fixed tiling approach.
In the next section we give background on the RL-
SANE algorithm we use for dimensionality reduction.
Next, the Maximum Density Separation algorithm is
introduced and explained in detail. This method is
then applied to the two problems given in Section 4,
and the results of this study are given in the Section 5.
Finally, the paper concludes with a summary of our
contributions and some future directions.
2 BACKGROUND
The RL-SANE algorithm is a powerful reinforcement
learning and state abstraction algorithm (Wright and
Gemelli, 2009). It combines a neuroevolution ap-
proach to constructing neural networks (Stanley and
Miikkulainen, 2002) with a fixed tiling over a one di-
mensional abstract state space to allow a learner to ef-
ficiently solve complex problems by learning the op-
timal action for each tile in this abstract space. An
overview of this process is given in Figure 1.
For any dimensionality of input space S the artifi-
cial neural network (ANN) layer of RL-SANE takes
the input measured across m dimensions and reduces
it to a single output value z ∈ [0, 1] corresponding to
a single abstract state s
′
i
∈ S
′
. This one dimensional
output space still represents infinitely many states, so
a tiling is applied to it. The fixed tiling simply splits
S
′
into a number of equal sized tiles with no consid-
eration given to the exact position of where each split
occurs. The tile boundaries are suboptimal since no
consideration is given to how observations will gather
in the space. However, the ANNs used is this ap-
proach are not fixed. They are produced and adapted
through the use of the NEAT neuroevolutionary algo-
rithm (Stanley and Miikkulainen, 2002). The NEAT
algorithm adapts the ANNs to fit the observed ground
states to the structure of the abstract state space less-
ing the impact of a sub-optimal tiling. This ability of
RL-SANE to adapt to the structure of a specified ab-
stract state space improves its ability to discover π
∗
over other tile coding approaches.
The original RL-SANE algorithm included a user
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
250

specified parameter β to determine the number of
tiles to lay over S
′
. Evidence displayed in (Wright
and Gemelli, 2009) shows that the algorithm’s overall
convergenceis sensitive to β. In this paper we propose
an adaptive tiling approach to overcome RL-SANE’s
limitations and automatically find a good partition-
ing. We will show how this approach improves RL-
SANE’s ability to quickly convergeto an optimal pol-
icy and eliminates the need to derivean ideal β param-
eter.
3 MAXIMUM DENSITY
SEPARATION
The Maximum Density Separation (MDS) method is
a new approach to derive non-arbitrary discretizations
of the state space. The rationale for this approach is
that there may exist ANNs, used to abstract the state
space, in a population that would provide useful ab-
stractions but do not fit a predetermined tiling. MDS
designs tilings for each ANN based on observationsof
the ANN’s activation. This method intuitively views
dense clusters of observationsas belonging to a single
state, and abstracts the state space so that these dense
clusters are located on separate tiles from one another.
The split between tiles occurs at the farthest point be-
tween two dense regions of observations. This ap-
proach is principled by the idea that nearby states will
prefer the same action, however the size of each of
these groups may vary so we must use an adaptable
solution.
There are two main challenges related to the MDS
approach, the first is how to estimate the density of the
space or otherwise cluster observations, and the sec-
ond is deciding the appropriate time to reassess the
abstraction. In the context of the first problem, MDS
can be thought of as a framework where an appro-
priate clustering or density estimation technique can
be applied at the discretion of the user. In this work,
we model the density of the abstract state space using
a simple histogram approach as it does not require
much additional computation to employ within the
learning algorithm. We partition the one dimensional
space into 1000 equal width bins in our approach.
The number of bins can be taken as a parameter to
the method, however, we found that the algorithm is
not very sensitive to this value. One possible limita-
tion of this simple technique is if all observed states
fall into only a few adjacent bins. This will cause the
algorithm to be unable to find a new partitioning be-
cause there would seem to be only one peak. To com-
bat this and similar situations other clustering or den-
sity estimation techniques may be used. For example,
since we are only interested in the most dense areas of
the space, a kernel density estimation method like the
mean shift algorithm may be employed (Comaniciu
and Meer, 2002). While more complicated clustering
or density estimation methods can be used, the trade
off in terms of possibly more accurate state boundary
identification must be balanced against the time cost
of performing the analysis, which will depend on the
chosen algorithm.
Determining when to repartition the abstract space
can have a large impact on the convergence speed of
the learning algorithm. If the tiles are repartitioned
too frequently the learner may not have time to learn
accurate Q-values on the abstract states, causing the
algorithm to converge to a less than optimal policy.
On the other hand, attempting to learn in a poorly
partitioned space can lead to wasted update cycles as
the Q-values do not give meaningful direction to the
learner. In our implementation of MDS we reparti-
tion the space whenever a failure state is reached by
the learner since it is possible that a new partitioning
might help the learner avoid failing the problem in a
subsequent attempt.
An overview of the MDS method is given in Al-
gorithm 1. For a single run of the problem in a given
RL algorithm, this method records the frequency of
observations across the state space until a failure or
goal state is reached. On a failure, the constructed fre-
quency distribution is searched for relative extrema,
using a soft-thresholding approach to prevent small
fluctuations in the distribution from leading to many
spurious extrema. For example, if consecutive bins
in the histogram respectively include 9, 8, and 10 ob-
servations, peaks are not placed in both the 9 and 10
bins because there was not enough of a decrease be-
tween them. This area is instead treated like a plateau
in the distribution. Once the relative extrema have
been identified, a partition is placed in the space in the
center of every two relative maximums. The splits be-
tween abstract states are made in this fashion in accor-
dance with the maximum margin principle (Mitchell,
Algorithm 1: Maximum Density Separation (MDS).
required: number of bins for frequency distribution
output: new abstract state mapping
≪embedded within an RL algorithm≫
get next state s
′
by following π
∗
from state s
if s
′
!= fail state
s := s
′
increment frequency distribution (s)
else if s
′
== fail state
locate relative extrema in frequency distribution
erase old tiles of S
′
partition S
′
in the center of two rel. maximums
end else if
AUTOMATIC STATE SPACE AGGREGATION USING A DENSITY BASED TECHNIQUE
251

1997), which seeks to minimize the structural vari-
ance in a hypothesis. Positioning the splits as far as
possible from the dense regions of observations mini-
mizes the risk that in the next run of the problem new
observations belonging to one dense region will spill
into an adjacent state and mislead the learning there.
This process is linear in the number of bins used to
measure the frequency distribution, and in practice
had only a negligible impact on the running time of
each generation of the algorithm, and so is a feasible
abstraction algorithm in terms of time complexity.
MDS effectively overcomes the limitations of the
fixed tiling: abstract state partitions can be placed
anywhere in the space and actively work to fit the out-
puts of the neural networks. This allows the bound-
aries to dynamically fit the outputs instead of depend-
ing on expensive evolution to fit the neural networks
to the abstract states. The MDS method does intro-
duce some other limitations, however. It could be the
case that an area of dense observations is not really
homogeneous in terms of preferred action, but were
coincidentally grouped together by the ANN. In this
case, the abstract states might still become successful
if the ANN adapts and separates these states into two
different clusters in a later evolutionary stage. An-
other concern is the additional computational burden
if a more complicated clustering/density estimation
method was used, however our results show that the
simple frequency based approach taken here can be
effective.
4 EXPERIMENTAL SETUP
Here we see what benefit MDS gives the RL-SANE
algorithm in terms of convergence speed and number
of abstract states in the solution. In addition to com-
paring the automatic MDS method against the fixed
tiling of RL-SANE, we include another algorithm in
the study, a mutation method which allows RL-SANE
to mutate the number of abstract states during the evo-
lution of the network. The experiments are carried out
on two benchmark RL problems, mountain car and
double pole balance.
The mutation method simply introduces another
mutation operator into the neural network’s evolution-
ary process which changes the number of tiles used in
the abstraction in the next generation. The number
of tiles can either increase or decrease up to five val-
ues per mutation so that each subsequent abstraction
is somewhat similar to the preceding one. The muta-
tion method is not completely automatic; the number
of tiles to start with will have an impact on how the
algorithm performs. We also present a brief study of
this phenomenon in the results.
The mountain car problem (Boyan and Moore,
1995) consists of a car trying to escape a valley as
illustrated in Figure 2a. The car starts at a random po-
sition in the valley and its goal is to drive over the hill
to the right of the starting position. Unfortunately, the
car’s engine is too weak to drive up the hill directly.
Instead, the driver must build momentum by driving
forward and backward in order to escape the valley.
Only two perceptions are used to define this prob-
lem, the position of the car within the valley X, and
the velocity of the car V. Time is discretized into
small intervals and the learner can choose one of two
actions in each time step: drive forward or backward.
The only reward that is assigned is -1 for each each
action that is taken before the car reaches the goal
of escaping the valley. Since RL algorithms seek to
maximize the reward, the optimal policy is the one
that enables the car to escape the valley as quickly as
possible.
The double inverted pole balancing prob-
lem (Gomez and Miikkulainen, 1999) depicted in
Figure 2b is a very difficult RL benchmark problem.
In this problem, the learner must balance two poles
of different length and mass which are attached to a
moving cart. The problem is further complicated by
maintaining that the cart must stay within a certain
small stretch of track. If the learner is able to prevent
the poles from falling over after a specified amount
of time then the problem is considered solved.
This is a higher dimensional problem than the
mountain car problem, with six perceptions being
given to the learner: the position of the cart X, the
velocity of the cart X
′
, the angle each beam makes
with the cart, θ
1
and θ
2
, and the angular velocities of
the beams, θ
′
1
and θ
′
2
. Once again, time is discretized
into small intervals, and during any such interval the
learner can choose to push the cart to the left or right
or to leave it alone. In our experiment, the learner
only receives a -1 reward for dropping either beam or
exceeding the bounds of the track. If the learner is
able to balance two poles and not exceed the bounds
of the track for 10
6
time steps the problem is taken to
be solved.
On each of the problems the three methods were
evaluated over 25 runs using different random seeds
(the same seed values were used for all three meth-
ods). For each run, both the mountain car and double
pole balance environments used a problem set size of
100 random initial start states. We report the aver-
age values across the 25 runs in our results. It should
be noted that the mutation and the fixed tiling ap-
proaches have a significant dependency on the initial
number of abstract states, while the MDS does not.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
252
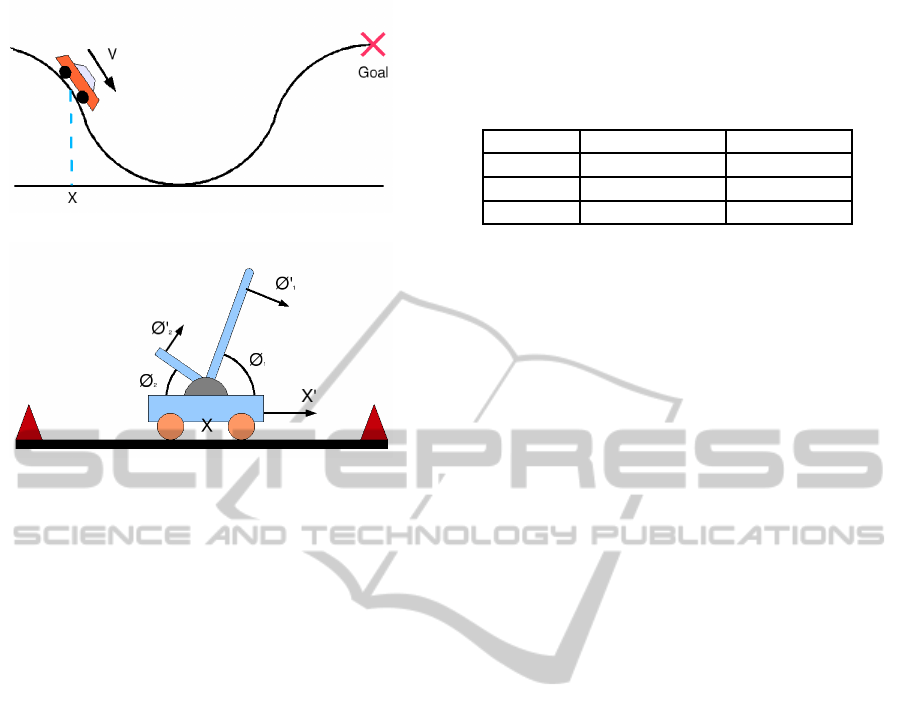
(a)
(b)
Figure 2: Depictions of the mountain car (a) and double
pole balance (b) problem domains.
In the mutation and fixed methods we experimented
with setting the number of initial abstract states from
10, 20, . . . , 100 and the results show either the aver-
age performance of the algorithm over all of these
boundaries, or the best performer from the 10, as in-
dicated. For the RL-SANE algorithm with a fixed ab-
straction, these initial states cannot change during the
learning process, while the mutation method is free to
alter them over time. The MDS method begins with
an arbitrary abstraction over the state space which is
quickly replaced by a more competent estimate after
the first attempt at learning the problem.
The RL-SANE algorithm was set to use a popu-
lation of 100 neural networks per generation, with a
maximum of 200 generations of learning. Neuroevo-
lution is provided by Another NEAT Java Implemen-
tation (ANJI) (James and Tucker, 2004). We used the
Sarsa(λ) learning algorithm with learning and neu-
roevolution parameters set as in (Wright and Gemelli,
2009), and we also limited each learning episode of
the mountain car to 2500 time steps to ensure ter-
mination. The mutation method was allowed to al-
ter the number of states by up to 5 per generation to
provide regularity between generations of neural net-
works. For MDS the density of the observations in the
state space was estimated using a histogram of 1000
evenly spaced bins to collect observations. The exact
value of this parameter is unimportant as long as it is
significantly larger than the number of expected ab-
stract states in the solution and an episode produces
enough observations to partially fill in the space.
Table 1: Average number of final abstract states used ±
standard deviation for MDS and the number of initial states
used to derive the best performance for the mutation and
fixed approaches.
Mountain Car Double Pole
MDS 3.36 ± 1.25 13.5 ± 5.93
Mutation 90 10
Fixed 50 10
5 EXPERIMENTAL RESULTS
5.1 Mountain Car
Figure 3 shows the average number of time steps
taken to leave the valley over the 25 runs for the three
methods. Fewer steps are better. The fixed and muta-
tion curves shown use the best choice of initial num-
ber of abstract states, although all values attempted
gave similar results for this problem and so are omit-
ted for clarity. The mutation method found the opti-
mal policy fastest with 90 initial states, and the fixed
approach did the best on 50 states. The mountain car
problem shows all of the methods performing very
similarly and all rapidly converging to a policy that
takes on average approximately 50 time steps to nav-
igate the car from the valley. The Maximum Den-
sity Separation method lags slightly behind the other
two methods, which indicates that this problem can
be easily learned without complicated abstract state
repartitioning.
Analysis of Table 1 gives an additional explana-
tion for the performance of MDS. The MDS method
consistently finds that there are only roughly three
groups of observations in the space and so only parti-
tions the space into three tiles. It might have taken
additional generations to effectively learn the cor-
rect placement of these partitions, compared with the
larger number of states used by the mutation and fixed
methods. Even though the other methods need to
learn correct values over more states, there are still
relatively few states to learn so they quickly converge.
These results do serve to show that automatic reparti-
tioning of the abstract state space does not degrade the
convergence of the learning algorithm much in prob-
lems where fixed tiling are sufficient.
Table 1 contains the number of abstract states
available to the fixed and mutation methods during
their best run, as well as the number of states that
was determined by the MDS method. We can see
that the MDS method on average uses 3 or 4 abstract
states with a standard deviation of 1.25, meaning that
it was very consistent in the number of states used
AUTOMATIC STATE SPACE AGGREGATION USING A DENSITY BASED TECHNIQUE
253
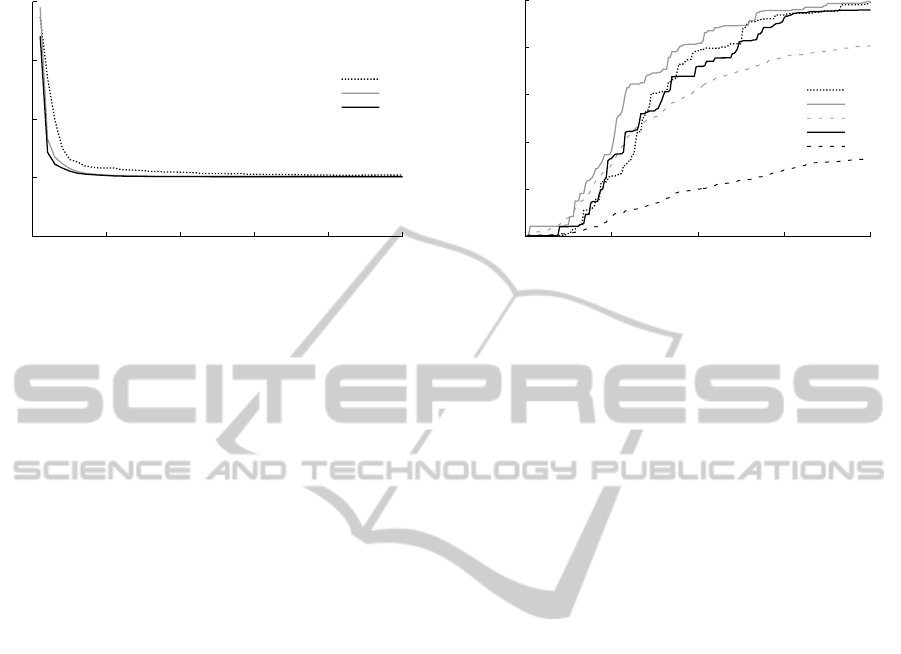
0
50
100
150
200
0 10 20 30 40 50
Time Steps
Generations
Mountain Car
Performance
MDS
Mutation
Fixed
Figure 3: The performance of MDS, mutation and the fixed
abstraction methods on the mountain car. The curves for
the mutation and fixed methods are the results from the best
initial parameter settings.
to learn the problem. The other two methods pre-
ferred many more partitions. However, the number
of those partitions where observations were placed
by the ANNs in the RL-SANE procedure were much
smaller. The fixed method used roughly 19.08 ± 9.08
(average±std) out of the 50 available states, while the
mutation method used 30.40± 22.67 from 90 possi-
ble starting states. From this we can see that it is not
only the number of tiles that is important, but the ef-
fect they have on where the tiles get placed across the
abstract state space. Since each of these two methods
use fixed-width partitioning, the number of abstract
states will cause the boundaries to fall in different
locations, and over-partitioning the space can allow
the learner to use more appropriately positioned tiles.
This is in contrast to the MDS approach which allows
the boundaries to be placed anywhere in the abstract
state and does not need to add additional empty states
solely to adjust the layout of the useful ones.
Another insight that Table 1 brings is that MDS
has by far the most compact and efficient abstraction
for the mountain car problem. Reducing an infinite
state space to such a compact representation is one
of the most important abilities of an abstraction tech-
nique. The fact that MDS is able to achieve such a
representation suggests that it may allow RL algo-
rithms to scale to more complicated problems better
than the other methods shown here.
The disparity in the number of used states between
three methods is interesting. Two possible explana-
tions regarding why the fixed and mutation methods
had a large number of states are that the large num-
ber of initial states induced the learner and ANN to
prefer many small groups of observations throughout
the one dimensional state space, or that many adjacent
states shared the same optimal action preference. In
0
20000
40000
60000
80000
100000
0 50 100 150 200
Time Steps
Generations
Double Pole Balance
Performance
MDS
Mutation Best
Mutation Avg
Fixed Best
Fixed Avg
Figure 4: Learning performance evaluation for each of the
three methods. For comparison, the mutation and fixed
methods include their single best initial parameter setting
as well as their average performance across all parameter
values.
the latter case, these adjacent states could have been
merged together resulting in possibly far fewer states,
though there is no means to do this in these methods.
5.2 Double Pole Balance
Figure 4 shows the average number of time steps the
pole was balanced for each of the three methods, the
solid lines for the mutation and fixed methods are
the best scores achieved by any initial parameter set-
ting (10 states for both methods). The more time
steps, the better the algorithm has learned the prob-
lem. The dashed curves show the average perfor-
mance for the two methods across all tested initial
state boundaries. The MDS has no initial parame-
ter selection and so only has the single dotted line in
the figure. We can see that MDS and the best set-
tings of the other methods show similar trends, with
the score of the two adaptive methods just edging out
the best fixed method. Analysis of the average curves
(dashed lines) gives more information about the gen-
eral performance of the mutation and fixed methods
as compared to the MDS method. While the MDS
method has no choice of initial parameters and still
ends up achieving an excellent overall score, differ-
ent numbers of initial abstract states causes a varied
performance in the other two methods. The mutation
method is relatively robust with regard to the initial
parameter selection as compared to the performance
degradation seen by the fixed method if a bad initial
abstraction is selected.
Figure 5 explores this phenomenon more com-
pletely by showing the performance of the fixed and
mutation methods for all 10 initial parameter settings.
The individual parameter results are shown in faint
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
254
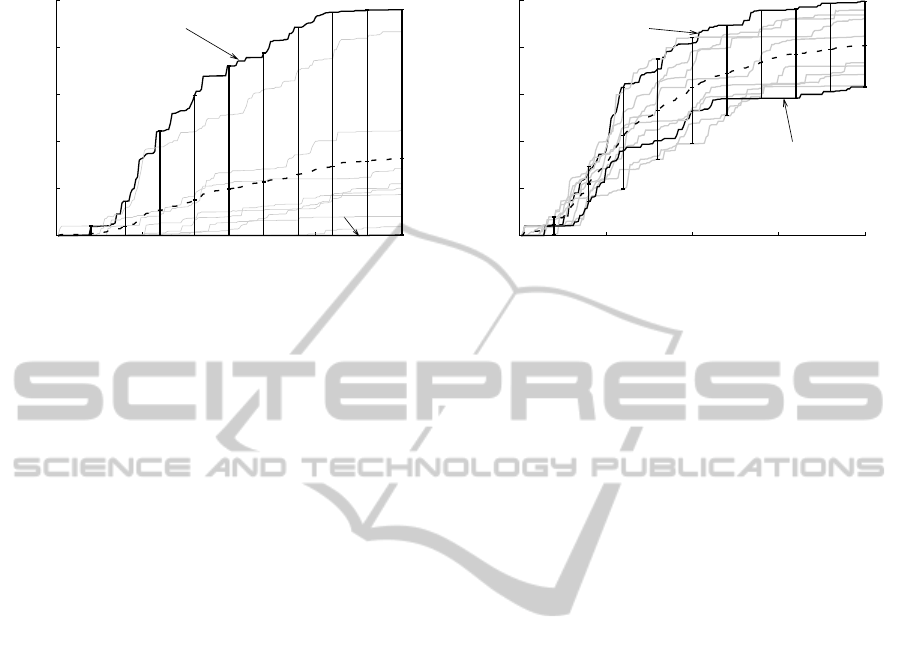
0
20000
40000
60000
80000
100000
0 50 100 150 200
Time Steps
Generations
Parameter Sensitivity
Fixed
10
100
0
20000
40000
60000
80000
100000
0 50 100 150 200
Time Steps
Generations
Parameter Sensitivity
Mutation
10
90
Figure 5: The effect of different numbers of initial abstract states for both the Fixed and Mutation methods on the Double Pole
Balance problem. The dashed line is the average of all values; vertical bars show distance between maximum and minimum
performance.
gray lines except for the best and worst performers
which are solid black lines. The vertical bars span
the space between the best and worst performer and
highlight the sensitivity of the fixed method. Gener-
ally, the smaller parameters perform better than the
larger initial values, and the vertical bars show that
the fluctuation of performance is much smaller in the
mutation method than the fixed method. The rea-
son why the double pole balance problem is much
more sensitive to the initial number of abstract states
as compared to the mountain car problem has to do
with the number of actively used states. In the moun-
tain car problem, as discussed in Section 5.1, even
if many states were available only a fraction of them
were used. This is in contrast to the double pole bal-
ance problem where nearly all of the available states
are used. The mutation method allows the number of
available states to quickly be reduced down to a num-
ber that the learning algorithm can deal with, and thus
improve the rate of convergencecompared to the fixed
method.
All three abstraction methods prefer to use a sim-
ilar number of abstract states for the double pole bal-
ance problem, as indicated by Table 1. The best
fixed tiling began with 10 tiles and used all 10 con-
sistently throughout the learning process. The mu-
tation method also achieved its best performance af-
ter starting with 10 tiles, however the number of tiles
used decreased to 7.56± 3.88 by generation 200. The
MDS method was also in agreement with the other ap-
proaches and by generation 200 was using 13.5± 5.93
tiles. Despite the complexity of the problem, many of
the states in the ground state space can be success-
fully aggregated together, as evidenced by the small
number of states being used.
6 CONCLUSIONS AND FUTURE
DIRECTIONS
We have presented the Maximum Density Separation
algorithm which seeks to automatically partition a
state space based on dense regions of observations.
This method has been shown to improve the learn-
ing rate as compared to using a fixed abstraction or
na¨ıvely altering the number of states during evolution
on the double pole balance problem. MDS did not im-
prove the rate of convergenceon the mountain car, but
it was competitive while using an abstraction made of
far fewer abstract states compared to the others.
This work points to several promising future di-
rections. As illustrated by the mountain car results,
intelligent aggregation is not always beneficial. Iden-
tifying these situations during the abstraction genera-
tion procedure could be one future area of research.
Additionally, there is no need to limit MDS to the
one dimensional state space used by RL-SANE, and
applying this method to the ground state space or in
combinationwith a differentdimensionality reduction
technique may prove useful. In general, the interplay
between state abstraction and dimensionality reduc-
tion could be an interesting avenue of future research.
REFERENCES
Boyan, J. A. and Moore, A. W. (1995). Generalization in re-
inforcement learning: Safely approximating the value
function. In Advances in Neural Information Process-
ing Systems 7, pages 369–376. MIT Press.
Comaniciu, D. and Meer, P. (2002). Mean shift: A robust
approach toward feature space analysis. IEEE Trans.
Pattern Anal. Mach. Intell., 24(5):603–619.
AUTOMATIC STATE SPACE AGGREGATION USING A DENSITY BASED TECHNIQUE
255

Gomez, F., Schmidhuber, J., and Miikkulainen, R. (2006).
Efficient non-linear control through neuroevolution.
In Proceedings of the European Conference on Ma-
chine Learning, pages 654–662.
Gomez, F. J. and Miikkulainen, R. (1999). Solving non-
markovian control tasks with neuroevolution. In
In Proceedings of the 16th International Joint Con-
ference on Artificial Intelligence, pages 1356–1361.
Morgan Kaufmann.
James, D. and Tucker, P. (2004). A comparative analysis of
simplification and complexification in the evolution of
neural network topologies. In Proceedings of the 2004
Conference on Genetic and Evoluationary Computa-
tion (GECCO-04). Springer.
Li, L., Walsh, T. J., and Littman, M. L. (2006). Towards a
unified theory of state abstraction for mdps. In Pro-
ceedings of the Ninth International Symposium on Ar-
tificial Intelligence and Mathematics, pages 531–539.
Mccallum, A. K. (1996). Reinforcement learning with se-
lective perception and hidden state. PhD thesis, The
University of Rochester. Supervisor-Ballard, Dana.
Miller, W.T., I., Glanz, F., and Kraft, L.G., I. (1990). Cmas:
an associative neural network alternative to backprop-
agation. Proceedings of the IEEE, 78(10):1561 –1567.
Mitchell, T. (1997). Machine Learning. McGraw Hill.
Stanley, K. O. and Miikkulainen, R. (2002). Efficient
reinforcement learning through evolving neural net-
work topologies. In GECCO ’02: Proceedings of the
Genetic and Evolutionary Computation Conference,
pages 569–577.
Sutton, R. (1996). Generalization in reinforcement learn-
ing: Successful examples using sparse coarse coding.
In Advances in Neural Information Processing Sys-
tems, volume 8, pages 1038–1044. MIT Press.
Uther, W. T. B. and Veloso, M. M. (1998). Tree based dis-
cretization for continuous state space reinforcement
learning. In AAAI ’98/IAAI ’98: Proceedings of
the fifteenth national/tenth conference on Artificial in-
telligence/Innovative applications of artificial intelli-
gence, pages 769–774, Menlo Park, CA, USA. Amer-
ican Association for Artificial Intelligence.
Whiteson, S., Taylor, M. E., and Stone, P. (2007). Adaptive
tile coding for value function approximation. Tech-
nical Report AI-TR-07-339, University of Texas at
Austin.
Wright, R. and Gemelli, N. (2009). State aggregation
for reinforcement learning using neuroevolution. In
ICAART 2009 - Proceedings of the International Con-
ference on Agents and Artificial Intelligence, pages
45–52.
ICAART 2011 - 3rd International Conference on Agents and Artificial Intelligence
256
