TOWARDS A NEW HOMOGENEOUS IMMUNOASSAY

FOR GONADOTROPIN-RELEASING HORMONE BASED ON

TIME-RESOLVED FLUORESCENCE ANISOTROPY

Peter D. Dowd

Department of Bioengineering, University of Strathclyde, Wolfson Centre, 106 Rottenrow, Glasgow, U.K.

Jan Karolin, Carol Trager-Cowan, David J. S. Birch

Department of Physics, Centre for Molecular Nanometrology, University of Strathclyde, SUPA

John Anderson Building, 107 Rottenrow, Glasgow, G4 0NG, U.K.

William H. Stimson

Strathclyde Institute of Pharmacy and Biomedical Science, University of Strathclyde

Royal College, 204 George Street, Glasgow, U.K.

Keywords: Homogeneous immunoassay, Time-resolved fluorescence depolarisation, Gonadotropin-releasing hormone.

Abstract: A new method for detecting gonadotropin-releasing hormone type 1 (GnRH-1) is proposed. The method is

based on a fluorescence polarisation immunoassay where the GnRH-1 vies for the binding site on the anti-

GnRH (antibody 7B10.1D10) with a labelled peptide consisting of a fragment of GnRH labelled with

fluorescein. Time-resolved anisotropy decays indicate increased correlation times for the labelled fragment

in the presence of 7B10.1D10 compared with the correlation times for the labelled peptide fragment alone.

When GnRH-1 is added to the solution of the labelled peptide in the presence of 7B10.1D10 it has the effect

of reducing the correlation times. The results demonstrate the possibility of introducing the labelled

fragment as a competitor to the antigen in the fluorescence polarisation immunoassay for GnRH-1 and,

more generally, in the case where there is a disadvantage in labelling the antigen, such as GnRH-1, with a

fluorescent probe.

1 INTRODUCTION

In this report we describe a potential method for

detecting gonadotropin-releasing hormone type-1

(GnRH-1) using a fluorescence polarisation

immunoassay (FPI). Conventionally in FPI’s, an

antigen labelled with a fluorescent probe is displaced

from a specific antibody binding site by an

unlabelled antigen. In this method we have replaced

the labelled antigen with a labelled ‘fragment’ of the

antigen thus eliminating the problematic issues

surrounding GnRH-1.

GnRH-1 (the mammalian form of GnRH) is a

hypothalamic hormone and it plays a fundamental

role in the events leading to the synthesis and release

of leuteinising hormone (LH) and follicule

stimulating hormone (FSH) into the circulatory

system (Conn & Crowley, 1991). GnRH is essential

in reproductive function and expression of GnRH

has even been reported in tissues such as the ovary,

breast and prostate (Chen et al, 2002). Although

GnRH influences conditions such as GnRH-

dependent precocious puberty, the expression of

GnRH in tissue areas outside the hypothalamic

region and in the immune system is not fully

understood. Nevertheless, due to the suggestion that

GnRH expression maybe a possible marker for

certain tumours and the success of GnRH agonists

used in a variety of disorders, monitoring the levels

and effects of GnRH are of significant clinical

interest (Tanriverdi et al, 2004).

FPI’S are appealling for medical diagnostic and

point of care testing (POC) applications because

they can be performed in a homogeneous format and

184

Dowd P., Karolin J., Trager-Cowan C., S. Birch D. and Stimson W..

TOWARDS A NEW HOMOGENEOUS IMMUNOASSAY FOR GONADOTROPIN-RELEASING HORMONE BASED ON TIME-RESOLVED FLUORES-

CENCE ANISOTROPY.

DOI: 10.5220/0003152001840188

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2011), pages 184-188

ISBN: 978-989-8425-37-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

with relatively few preparation steps (Price, 2001).

Using antigens labelled with fluorescent markers,

FPI’s rely on the difference in anisotropy (or

polarisation) measurements of a labelled antigen

compared with the anisotropy of the labelled antigen

in association with an antibody (Terpetsching et al,

1994). More specifically, in FPI’s the emission

from the free labelled antigen must be depolarised.

Thus the rotational correlation time for the antigen

must be much shorter than that of the probe.

Therefore, when this method is applied to antigens

with a low molecular weight, fluorescein with a

lifetime near 4ns is typically chosen as the

fluorescent probe (Spencer et al, 1973). In

comparison with the free labelled antigen the

polarisation will increase when the labelled antigen

binds to the antibody.

In the case of GnRH-1, labelling demands either

the addition or removal of an amino acid. The

addition of an amino acid can lead to an alteration in

conformation due to the increase in size and change

in charge. This is less likely to occur if an amino

acid is removed. Therefore, in an attempt to preserve

the antibody binding site which is in the centre of

the peptide (Khan et al, 2003), we describe a method

that incorporates the 9-amino acid fragment of

GnRH-1 labelled with fluorescein to act as a

replacement for the conventional labelled antigen in

the assay. Furthermore, we use time-resolved

anisotropy techniques in an effort to reveal any

underlying issues that may arise from using the

labelled fragment in place of the labelled antigen.

Fluorescence spectroscopy is a technique that offers

sensitivity down to a single-molecule level, with a

signal-to-niose ratio that improves with

measurement duration, and is therefore well placed

for the development of ultrasensitive biosensors

such as fluorescence-based immunoassays.

2 THEORY

The timed-resolved fluorescence anisotropy, r(t), is

an angular correlation function that conveniently is

defined as (Lakowicz, 2006)

() ()

()

() 2 ()

vv vh

tIt

−

(1)

where I

(t) and I

(t) are the recorded fluorescence

intensities at time t following an excitation event at t

= 0, and where the first and second subscript refers

to the orientation of the excitation and emission

polariser respectively. In the simplest case, with a

fluorophore rigidly attached to a macromolecule that

undergoes free isotropic rotational diffusion, the

anisotropy is described by a mono-exponential

decay function

() exp

lobal

rt r

⎛⎞

=−

⎜⎟

⎝⎠

(2)

The time-zero ansiotrpoy r

can take the maximum

value 0.4 for one-photon excitation (assuming the

transition dipoles for absorption and emision are

parallel). The correlation time

global

is related to the

hydrodynamic volume, V, of the macromoleule and

can be calculated form the Stokes-Einstein Debye

relationship

global

= (3)

wher

is the viscosity of the solvent, k

Boltzmann

constant and T the absolute temperature.

It is often observed when analysing the

fluorescence anisotropy recorded from fluorescently

labelled macromolecules, for example proteins, that

the anisotropy expression is given by a bi-

exponential decay law

() exp exp

local global

rt b b

φφ

⎛⎞

=−+−

⎜⎟

⎝⎠

(4)

The correlation times are then often interpreted to

reflect on a local wobbling motion of the

fluorophore in its binding site,

local

, and an overall

rotational diffusion of the macromolecule,

global

. If

global

, it will not be resolved in a time

correlated single-photon counting experiment, and

will only be evident by a plateau value of value r

∞

. If

there is also a fraction of free fluorophore that is not

bound to the macromolecule, as in our case, there

might be a fraction of the antigen that is not bound

to the antibody and then the anisotropy expression

reads

() exp exp

free local

rt b b r

φφ

∞

⎛⎞

−+ − +

⎜⎟

⎝⎠

(5)

In the present work anisotropy data was analysed

according to equation (5).

TOWARDS A NEW HOMOGENEOUS IMMUNOASSAY FOR GONADOTROPIN-RELEASING HORMONE BASED

ON TIME-RESOLVED FLUORESCENCE ANISOTROPY

185

Figure 1: The pyroGlu on GnRH-1 is replaced by a fluorescein that is attached to the peptide backbone of the peptide

fragment by a caproic acid linker.

3 MATERIALS AND METHODS

GnRH-1 is a decapeptide with the amino acid

sequence pyroGlu

-His

-Trp-

-Ser

-Tyr

-Gly

-Leu

Arg

-Pro

-Gly

-NH

. GnRH-1 (cat. no. L7134) and

[des-pGlu

]-RH-LH (cat. no. L8762) were purchased

from Sigma-Aldrich, Inc. The labelled fragment

([des-pGlu

]-RH-LH-Acp-FITC) was purchased

from GL Biochem (Shanghai) Ltd (Figure 1).

Antibody specific to GnRH-1 was produced from

the monoclonal antibody secreting cell line,

7B10.1D10, by using standard cell culture

techniques (Khan et al, 2003). From experiment, the

antibody was found to have an IgG

isotype and was

shown to bind to both GnRH-1 and [des-pGlu

]-RH-

LH by ELISA. The antibody was also shown to bind

to Protein L agarose resin purchased from Pierce

(cat. no. 20510) thus implying that the antibody has

kappa light chains and, more specifically, VκI light

chains. The Protein L agarose resin was used in the

antibody purification procedure following the Pierce

protocol. All solutions for fluorescence

measurements were prepared using a 20 mM sodium

phosphate buffer, pH 7.4.

Time-resolved fluorescence and anisotropy

decay time measurements were performed using the

time-correlated single photon counting technique

(TCSPC) on a FluoroCube (Horiba Jobin Yvon IBH

Ltd, Glasgow), (Apperson et al, 2009). The

excitation source was a 482 nm PicoBrite running at

10 MHz repetition rate and with an instrumental full

width half maximum of 50 ps. The emitted

fluorescence was observed on a TBX-04 detector

and data was analysed in IBH DAS6 software suite.

In the first instance the purpose of the

experiment was to compare the time-resolved

fluorescence measurements of the labelled fragment

with those from the labelled fragment in the

presence of the antibody 7B10.1D10 to confirm that

the altered GnRH structure could be captured by the

antibody. Secondly, it was to assess that the effect

could be reversed by adding GnRH-1 to the mixture

(Figure 2).

Figure 2: Schematic illustrating the initial bulk solution

condition where it is most likely that one labelled

fragment is bound to the antibody and the end bulk

solution condition where the antibody binding sites are

most likely to be occupied by GnRH-1.

The time-resolved fluorescence, recorded in the

magic angle condition, and anisotropy decays of six

different mixtures (Table 1) were measured.

Solution A contained the labelled fragment and

solution B contained the labelled fragment in the

presence of antibody where the number of potential

antibody binding sites is much greater than the

number of labelled fragment molecules in the

solution. GnRH-1 is added to the mixture giving

solutions C-F.

Table 1: The concentrations of antibody, labelled fragment

and GnRH-1 for each mixture.

sample [7B10.1D10]

μM

[labelled fragment]

[GnRH-1]

A - 4.94 -

B 0.33 1.97 -

C 0.33 1.10 0.56×10

-6

D 0.11 0.66 1.13×10

-3

E 0.11 0.66 1.69×10

-3

F 0.11 0.65 5.61×10

-3

Labelled fragment

bound to antibody

GnRH-1

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

186

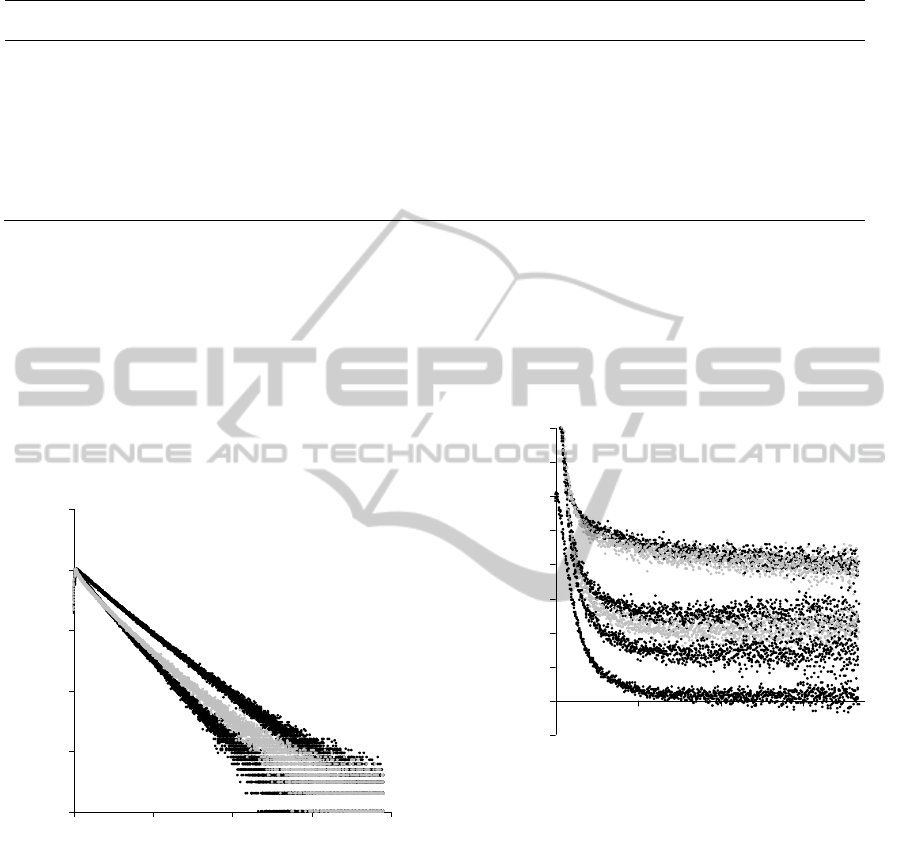
Table 2: Lifetimes resolved into two components

and

and also anisotropies at r

, r

∞

and correlation times

for all

solutions.

sample

/ ns

/ ns χ

/ ns

/ ns r

∞

A 0.76 (8.94%) 2.88 (91.06%) 1.03 0.34 0.22 (29.7%) 0.59 (70.3%) 0.00 1.00

B 1.17 (4.82%) 4.09 (95.18%) 1.03 0.49 1.70 (78.1%) 0.16 (21.9%) 0.20 1.06

C 0.93 (5.46%) 3.99 (94.54%) 1.17 0.37 0.96 (67.7%) 0.24 (32.3%) 0.21 1.10

D 0.61 (10.19%) 3.25 (89.71%) 1.43 0.31 0.00 (0.0%) 0.41 (100.0%) 0.13 1.18

E 0.68 (10.55%) 3.26 (89.45%) 1.43 0.36 0.14 (9.4%) 0.43 (90.6%) 0.10 0.94

F 0.90 (13.98%) 3.21 (86.02%) 1.21 0.37 0.12 (10.8%) 0.47 (89.2%) 0.07 1.03

4 RESULTS

On examining the time-resolved intensity decay

times of each mixture it is evident that the decay

time must be resolved into two or more components.

Analysis for two components is shown in Table 2.

The trend is more clearly shown qualitatively in the

decay curves.

100

1000

10000

100000

0 10203040

Time /ns

Counts

Figure 3: Time-resolved decays showing qualitatively the

difference between decay times of the labelled fragment

(A), the labelled fragment in the presence of antibody (B)

and when an excess of GnRH-1 is added to the solution

(D).

The most dramatic changes are shown in Figure

3 where the greatest difference in the decay time is

seen between the labelled fragment (A) and the

labelled fragment in the presence of antibody

(B).When an excess of GnRH-1 is added to the

solution (D) the mean decay time is reduced and the

photophysics is also altered.

A similar pattern is repeated in the time-resolved

anisotropy measurements and the greatest change in

anisotropy occurs between the labelled fragment (A)

and the labelled fragment in the presence of

antibody (B) (Figure 4).

-0.05

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0246

Time /ns

Anisotropy

Figure 4: Time resolved anisotropy decays for all

solutions. The anisotropy reduces as more GnRH-1 is

added to the solution (C-F).

As more GnRH-1 is added to the solution the

anisotropy falls suggesting that more of the labelled

fragment is spending more time free in solution than

bound to the antibody thus revealing the competition

between the labelled fragment and the GnRH-1 for

the 7B10.1D10 binding sites. Time-resolved

anisotropy decay measurements reveal information

about the rotational motion of the labelled peptide

molecules. Again, in almost all cases there are two

significant contributions to the rotational motion but

no attempt has been made as yet to explain the

results quantitatively.

TOWARDS A NEW HOMOGENEOUS IMMUNOASSAY FOR GONADOTROPIN-RELEASING HORMONE BASED

ON TIME-RESOLVED FLUORESCENCE ANISOTROPY

187

5 CONCLUSIONS

As a first step in designing an FPI for GnRH-1 we

used time-resolved fluorescence techniques (where

the antigen GnRH-1 competes with a synthetic

labelled fragment for the binding sites on the

specific GnRH-1 antibody). We demonstrated

qualitatively that the labelled fragment can bind to

the antibody and that competition between the

labelled fragment and the GnRH-1 for the binding

sites on the antibody 7B10.1D10 does occur.

ACKNOWLEDGEMENTS

This work was supported by a grant from the

EPSRC to the University of Strathclyde Medical

Devices Doctoral Training Centre.

REFERENCES

Apperson, K., Karolin, J., Martin, R. W., Birch, D. J. S.,

2009 Nanoparticle Metrology Standards Based on

Time-resolved Fluorescence Anisotropy of Silica

Colloids. Meas. Sci. Technol. 20, 025310

Chen, A., Kaganovsky, E., Rahimipour, S., Ben-Aroya,

N., Okon, E., Koch, Y., 2002 Two Forms of

Gonadotropin-releasing Hormone (GnRH) are

Expressed in Human Breast Tissue and Over

expressed in Breast Cancer: A Putative Mechanism for

the Antiproliferative Effect of GnRH by Down-

Regulation of Acidic Ribosomal Phosphoproteins P1

and P21. Cancer Research. 62, 1036–1044

Conn, P. M., Crowley, W. F., Jr. 1991 Gonadotropin

releasing Hormone and its Analogues. N. Engl. J.

Med. 324, 93-103

Khan M. A. H., Ferro V. A., Stimson W. H. 2003 Use of a

Highly Specific Monoclonal Antibody Against the

Central Variable Amino Acid Sequence of

Mammalian Gonadotropin Releasing Hormone to

Evaluate GnRH-1 Tissue Distribution Compared with

GnRH-1 Binding Sites in Adult Male Rats. AJRI. 49,

239-248

Lakowicz J. R., 2006 Principles of Fluorescence

Spectroscopy, 3rd ed. Kluwer Academic/Plenum

Publishers, New York City, New York

Price, C. P., 2001 Clinical Review: Point of Care Testing.

BMJ, 322, 1285-1288

Spencer, R. D., Toledo, F.B., Williams, B.T., and Yoss,

N.L 1973 Design, Construction, and 2 Applications

for an Automated Flow-cell Polarization Fluorometer

with Digital Read Out-Enzyme-Inhibitor (Antitrypsin)

Assay and Antigen-antibody (Insulin-insulin

Aantiserum) Assay. Clin. Chem. 19, 838-844

Tanriverdi, F., Silveira, L., Ganzalez-Martinez, D., Hu,Y.,

Bouloux, P., Kelestimur, F. 2004 Gonadotropin-

releasing Hormone Type-I (GnRH-1) Expression in

Peripheral Lymphocytes Aand Possible Immune

Action. Erciyes Tıp Dergisi (Erciyes Medical

Journal). 26 (3), 105-112

Terpetsching, E., Szmacinski, H., Lakowicz J. R., 1995

Fluorescence Polarization Immunoassay of a High-

Molecular-Weight Antigen Based on a Long-Lifetime

Ru-Ligand Complex. Anal. Biochem. 227, 140-147

BIODEVICES 2011 - International Conference on Biomedical Electronics and Devices

188