ON VACCINATION CONTROLS FOR THE SEIR EPIDEMIC

MODEL WITH SUSCEPTIBLE PLUS IMMUNE

POPULATIONS TRACKING THE WHOLE POPULATION

M. De la Sen, S. Alonso-Quesada

Department of Electricity and Electronics, Faculty of Science and Technology, University of the Basque Country

Campus of Leioa, 48940-Leioa, Bizkaia, Spain

A. Ibeas

Departmento de Telecomunicación e Ingeniería de Sistemas, Escuela Técnica Superior de Ingeniería

Universitat Autònoma, Barcelona, Spain

Keywords: Epidemic models, Control, SEIR epidemic models, Tracking objective, Vaccination control, Positivity

stability.

Abstract: This paper presents a simple continuous-time linear vaccination-based control strategy for a SEIR

(susceptible plus infected plus infectious plus removed populations) propagation disease model. The model

takes into account the total population amounts as a refrain for the illness transmission since its increase

makes more difficult contacts among susceptible and infected. The control objective is the asymptotically

tracking the joint susceptible plus the removed-by-immunity population to the total population while

achieving simultaneously the remaining population (i.e. infected plus infectious) to asymptotically tend to

zero.

1 INTRODUCTION

Important control problems nowadays related to Life

Sciences are the control of ecological models like,

for instance, those of population evolution

(Beverton-Holt model, Hassell model, Ricker model

etc.) via the online adjustment of the species

environment carrying capacity, that of the

population growth or that of the regulated harvesting

quota as well as the disease propagation via

vaccination control. In a set of papers, several

variants and generalizations of the Beverton-Holt

model (standard time-invariant, time-varying

parameterized, generalized model or modified

generalized model) have been investigated at the

levels of stability, cycle-oscillatory behavior,

permanence and control through the manipulation of

the carrying capacity (De la Sen, 2008a, 2008b, De

la Sen and Alonso-Quesada, 2008a, 2008b, 2009).

The design of related control actions has been

proved to be important in those papers at the levels,

for instance, of aquaculture exploitation or plague

fighting. On the other hand, the literature about

epidemic mathematical models is exhaustive in

many books and papers. A non-exhaustive list of

references is given in this manuscript (Erturk and

Momani, 2008, Keeling and Rohani, 2008, Khan et

al., 2009, Mollison, 2003, Mukhopadhyay and

Battacharyya, 2007, Ortega et al., 2003, Song et al.,

2009, Yildirim and Cherruault, 2009, Zhang et al.,

2009). The sets of models include the most basic

ones (Keeling and Rohani, 2008, Mollison, 2003):

• SI models where not removed-by-immunity

population is assumed. i.e., only susceptible and

infected populations are assumed,

• SIR models, which include susceptible, infected

and removed-by-immunity populations, and

• SEIR models where the infected populations is

split into the “infected”, which incubate the

disease but do not still have any disease

symptoms, and the “infectious” or “infective”,

which do have the external disease symptoms.

Those models have also two major variants,

namely, the so-called “pseudo-mass action models”,

where the total population is not taken into account

165

De la Sen M., Alonso-Quesada S. and Ibeas A..

ON VACCINATION CONTROLS FOR THE SEIR EPIDEMIC MODEL WITH SUSCEPTIBLE PLUS IMMUNE POPULATIONS TRACKING THE WHOLE

POPULATION .

DOI: 10.5220/0003152901650172

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 165-172

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

as a relevant disease contagious factor and the so-

called “true-mass action models”, where the total

population is more realistically considered as an

inverse factor of the disease transmission rates.

There are many variants of the above models, for

instance, including vaccination of different kinds:

constant (Yildirim and Cherruault, 2009), impulsive

(Song et al., 2009, Zhang et al., 2009), discrete-time

etc., incorporating point or distributed delays (Song

et al., 2009), oscillatory behaviors (Mukhopadhyay

and Battacharyya, 2007) and so on. In this paper, a

continuous-time vaccination control strategy is given

for a SEIR epidemic model which makes directly the

susceptible plus removed- by-immunity populations

to asymptotically track the whole population. It is

assumed that the total population remains uniformly

bounded through time while being nonnegative as

they are all the partial populations of susceptible,

infected, infectious and immune. Thus, the disease

transmission is not critical, and the SEIR-model is of

the above mentioned true-mass action type. Note

that although all the partial populations and the total

one are all nonnegative for all time in the real

problem under study, the property has to be

guaranteed for the mathematical SEIR-model (1)-(4)

as well.

2 SEIR EPIDEMIC MODEL

Let S(t) be the “susceptible” population of infection,

E(t) the “infected”, I(t ) the “infectious” population,

and R(t) the “removed by immunity” (or “immune”)

population at time t. Consider the SEIR-type

epidemic model:

()

S(t)I(t)

S(t) S(t) R(t) N(t) 1 V(t)

N(t)

=−μ +ω −β +ν −



(1)

S(t)I(t)

E(t) ( )E(t)

N(t)

=β − μ+σ



(2)

I(t) ( )I(t) E(t)=−μ+γ +σ



(3)

R(t) ( )R(t) (1 )I(t) N(t)V(t)=−μ+ω +γ −ρ +ν



(4)

subject to initial conditions

S(0) 0≥ , E(0) 0≥ ,

I(0) 0≥ and R(0) 0≥ under the vaccination

function

→\\, with

{}

zz0

∈≥\ \ .

The vaccination control is either the vaccination

function itself or some appropriate four dimensional

vector depending on it defined “ad-hoc” for some

obtained equivalent representation of the SEIR-

model as a dynamic system. In the above SEIR-

model, N(t) is the total population, μ is the rate of

deaths from causes unrelated to the infection,

the rate of losing immunity,

is the transmission

constant (with the total number of infections per

unity of time at time t being

S(t)I(t)

(t)

β ),

−

σ and

−

are, respectively, the average durations of the

latent and infective periods. All the above

parameters are nonnegative. The parameter

means the rate of immunity lost since it makes the

susceptible to increase and then the immune to

decrease. The usual simplified SEIR-model is

obtained with

=μ and

. In that case,

[]

N(t) S(t) E(t) I(t) R(t)

N(t) S(t) E(t) I(t) R(t) 0 t

N(t) S(t) E(t) I(t) R(t) N(0) N 0

=+++

=μ − − − − = ∀ ∈

⇒+++==>







>μ then the new-born lost of maternal

immunity is considered in the model. If

ν<μ then

there is a considered mortality incidence by external

causes to the illness. The parameter

(

]

0, 1ρ∈ is the

per-capita probability of dying from the infection. If

either

≠μ and

or ν=μ and

0ρ≠

, and

otherwise,

()N(t)

I(t)

ν−μ

ργ

occurs eventually on a

set of zero measure only, then the total population

varies through time as obtained by correspondingly

summing up both sides of (1)-(4). Furthermore, (1)

and (4) and (2) and (3) might be separately summed

up to obtain the evolution dynamics of the separate

populations of joint susceptible and immune and

joint infected and infectious. This leads to:

N(t) ( )N(t) I(t)= ν−μ −ργ



(5)

[

]

()

S(t) R(t) S(t) R(t)

S(t)

1 I(t) N(t)

N(t)

+=−μ+

⎛⎞

+γ −ρ−β +ν

⎜⎟

⎝⎠



(6)

[]

S(t)

E(t) I(t) E(t) I(t) I(t)

N(t)

⎛⎞

+=−μ + −γ−β

⎜⎟

⎝⎠



(7)

Note that (5) is identically zero if

0ν−μ=ρ=

From (5)-(7), it follows that:

()t ()(t)

N(t) e N(0) e I( )d

ν−μ ν−μ −τ

−ργ τ τ

∫

(8)

[

]

(t )

S(t) R(t) e S(0) R(0)

S( )

e N() (1 ) I()d

N( )

−μ

−μ −τ

+= +

⎡

⎤

⎛⎞

ν τ + γ −ρ −β τ τ

⎢

⎥

⎜⎟

⎝⎠

⎣

⎦

∫

(9)

[

]

(t )

E(t) I(t) e E(0) I(0)

S( )

eI()d

N( )

−μ

−μ −τ

+= +

⎛⎞

−

γ−β τ τ

⎜⎟

⎝⎠

∫

(10)

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

166

In order to further solve (9), an integration by parts

is performed as follows:

[]

tt t

(t )

00 0

( )dq(t, ) p( )q(t, )d N( )e d

N( )q(t, ) q(t, )N( )d

−μ −τ

ττ=τττ≡τ τ

=τ τ− τττ

∫∫ ∫

∫



(11)

where:

[]

(t )

q(t) e d q(t, )

q(t, t) q(t,0)

−μ −τ

−μ

⎡⎤

τ= = τ

⎢⎥

⎣⎦

−

==−

∫



(12)

so that q(t, t) 1/

=μ,

q(t,0) e /

−μ

=μ and then,

using (5) in (11) yields:

[]

(t ) t

(t )

N( )e d N(t) e N(0)

e ( )N( ) I( ) d

−μ −τ −μ

−μ −τ

⎡⎤

ττ=−

⎣⎦

−ν−μτ−ργττ

∫

(13)

which, after grouping identical terms, leads to:

(t )

t(t)

N( )e d

N(t) e N(0) e I( )d

−μ −τ

−μ −μ −τ

ττ

⎡⎤

=− +ργ ττ

⎢⎥

⎣⎦

∫

(14)

Thus, combining (9)-(10) and (14) yields:

[]

S(t) R(t) N(t) E(t) I(t)

S( )

e S(0) R(0) N(0) e I( )d

N( )

S( )

e E(0) I(0) e I( )d

N( )

−μ μτ

+−=− +

⎡⎤

⎛⎞

=+−+γ−βττ

⎢⎥

⎜⎟

⎝⎠

⎣⎦

⎡⎤

⎛⎞

=− + − γ−β τ τ

⎢⎥

⎜⎟

⎝⎠

⎣⎦

∫

(15)

3 VACCINATION CONTROL

If the control objective S(t) N(t) /=γ β for all time

is achieved with a positive vaccination control in

[]

0, 1 , it is proven below that the whole population

converges exponentially to the sum of the

susceptible population plus the immune population

while both the infectious and infective converge

exponentially to zero. This is theoretically the ideal

objective since the infection is collapsing as time

increases while the susceptible plus the immune

populations are approximately integrating the whole

population for large time. Other alternative objective

has been that the immune population be the whole

one but this is a more restrictive practical objective

since the whole susceptible population should

asymptotically track the immune one even those of

the susceptible who are not contacting the disease.

Theorem 1. Assume that

0β>γ≥

and that the

vaccination function is such that S(t) N(t) /=γ β

∀∈\ with a vaccination control in

[]

0, 1 for all

time. Then, the SEIR model (1)-(4) is positive for all

time. Furthermore,

[

]

[][]

S(t) R(t) N(t) E(t) I(t)

e S(0) R(0) N(0) e E(0) I(0)

−μ −μ

+−=− +

=+−=−+

(16)

for all time what implies the following constraint for

the initial conditions:

[]

N(0)

S(0) E(0) I(0) R(0)

γγ

== ++

ββ−γ

(17)

As a result,

[

]

[]

R(t) N(t) S(t) e E(0) I(0)

N(t) e E(0) I(0)

N(t) e R(0) S(0) N(t)

−μ

=−− +

β−γ

=−+

⎡⎤

β−γ β−γ β−γ

=+− ≤

⎢⎥

βγβ

⎣⎦

(18)

∀∈\ . Then, R(t) N(t)

β−γ

→

as t →∞.

Furthermore, the following two limits exist:

{

}

{

}

lim S(t) R(t) N(t) lim E(t) I(t) 0

→∞ →∞

−= +=

(19)

If, in addition,

−μ=ρ=

then

{

}

{} {}

(t) N(0) N lim S(t) R(t)

lim E(t) lim I(t) 0

→∞

→∞ →∞

=== +

(20)

Proof: The mathematical SEIR-model (1)-(4) is

positive since the vaccination control is in

[]

0, 1 for

all time so that no population takes negative values

at any time. On the other hand, (16) and (19) follow

directly from (15) and S(t) N(t) /=

γβ

for all time.

Finally, (20) follows from (16) and (19) since

−μ=ρ=

implies

(t) 0≡



∀∈\ , i.e.,

(t) N(0)≡

∀∈\ from (5). ***

An associate stability result follows:

Theorem 2. Assume that

0ργ ≥

. Then, the

following properties hold:

ON VACCINATION CONTROLS FOR THE SEIR EPIDEMIC MODEL WITH SUSCEPTIBLE PLUS IMMUNE

POPULATIONS TRACKING THE WHOLE POPULATION

167

(i) The SEIR-model is globally stable if

0 ≤ν≤μ

and the vaccination law fulfils

[]

V: 0, 1

→\ .

(ii) If

S(t) N(t) /=

γβ

and

0ν>μ≥

then the

conditions

{}

()

with 0

(0) e I( )d , lim N(t) 0

∞

ν−μτ

→∞

μ<ν<μ+ργ ργ>

=ργ τ τ =

∫

are jointly necessary for global stability under

Theorem 1.

(iii) If

0ν>μ≥

and I(t) ( )N(t)=ν−μ ργ

t t (finite)

∀≥ ∈\ then global stability of the

SEIR-model (1)-(4) is guaranteed if

[]

V: 0, 1

→\ . If

>μ≥

[

]

V: 0, 1

→\

and

I(t) ( )N(t)=ν−μ ργ is replaced with the

weaker condition

I(t) ( )N(t) o(e )

−α

−ν−μ ργ= for some

α∈\ then the SEIR-model (1)-(4) is globally

stable.

Proof:

(i)

0 ≤ν≤μ

and

0ργ ≥

then:

(t) ( )N(t) I(t) ( )N(t) 0=ν−μ −ργ ≤ν−μ ≤



∀∈\ so that N(t) N(0)≤<∞

∀∈\ . Since

the SEIR-model is positive if

[]

V: 0, 1

→\ then

all the populations are nonnegative and upper-

bounded by N(0).

(ii) On the other hand, the solution of (5) for any

initial conditions is:

()t ()

(t) e N(0) e I( )d

ν−μ − ν−μ τ

⎡⎤

=−ργττ

⎢⎥

⎣⎦

∫

which is uniformly bounded for all time only if

()

(0) e I( )d

∞

−ν−μτ

=ργ τ τ

∫

since

0ν>μ≥

. Also,

N(t) <∞

∀∈\ only if

(t) 0≤



on a non-

necessarily connected set of infinite Lebesgue

measure. Thus, there is a finite sufficiently large

finite time “t” such that:

[]

I(t) N(t) S(t) E(t) I(t) R(t)

1 I(t) S(t) E(t) R(t)

I(t) S(t) E(t) R(t)

ν−μ ν−μ

≥=+++

ργ ργ

⎛⎞

ν−μ ν−μ

⇔− ≥ + +

⎜⎟

ργ ργ

⎝⎠

ν−μ

⇔≥ + +

μ+ργ−ν

which requires the parametrical conditions

γ>

and

<ν<μ+ργ. Since I(t) is of exponential order

of at most

−

μ from Theorem 1 [see (16)] then

S(t) E(t) R(t)++ is also of exponential of order of

at most

−

μ so that N(t) extinguishes exponentially

as they do all the populations of susceptible,

infected, infectious and immune.

(iii) If

I(t) N(t)

ν−μ

ργ

with ν>μ after some finite

time

t then

N(t) N(t )

<∞

tt∀≥ and the

SEIR-model is positive since

[

]

V: 0, 1

→\ .

Thus, global stability follows. If

I(t) ( )N(t) o(e )

−α

−ν−μ ργ= replaces the above

stronger condition

I(t) ( )N(t)

ν−μ ργ after a

finite time then

(t)



is of exponential order

−

α so

that

)t(N is uniformly bounded for all time and the

global stability still holds. ***

3.1 Control Law Synthesis

Note that the case

>μ is not feasible in practice

for

γ=

since the population diverges. If

γ>

it requires a collapsing effect of the illness on the

population which is also unfeasible in practical

situations. It is now discussed how the vaccination

law is generated to keep simultaneously the SEIR-

model positivity plus the tracking objective of

Theorem 1 which requires positivity. The tracking

objective S(t) N(t) /

γβ for all time is equivalent

to any of the subsequent equivalent identities below:

[]

(t) N(t)/ E(t) I(t) R(t)

(t) E(t) I(t) R(t)

R(t) N(t) E(t) I(t)

γβ+++

⎛⎞

β−γ

⇔=++

⎜⎟

⎝⎠

⇔= ++

β−γ

⇔= −−

(21)

which requires as necessary condition

0β>γ≥

Although unrelated to the physical problem at hand,

the necessary condition will be also accomplished

with

and

≤

with S(t) N(t) /=γ β.

The solution of (4) matches (21) for all time if

and only if:

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

168

[]

(

)

()t ()

R(t) N(t) E(t) I(t) N(t) e E(0) I(0)

e R(0) e (1 )I( ) N( )V( ) d

−μ

−μ+ω μ+ωτ

β−γ β−γ

=−−=−+

ββ

=+γ−ρτ+ντττ

∫

(22)

where (10), with S(t) N(t) /=γ β, has been used.

Define an everywhere time-differentiable

auxiliary function

→\\ defined as:

[]

h(t) h(0) (1 )I( ) N( )V( ) d=+γ−ρτ+ντττ

∫

(23)

such that,

h(t) (1 )I(t) N(t)V(t)

V(t) h(t) (1 )I(t)

N(t)

=γ −ρ +ν

⎡⎤

⇔= −γ−ρ

⎣⎦



(24)

for all time so that the last right-hand-side additive

term in (23) becomes after integration by parts:

()t ()

()t()t ()

eeh()d

e e h(t) h(0) ( ) e h( )d

−μ+ω μ+ωτ

−μ+ω μ+ω μ+ωτ

ττ

⎡⎤

=−−μ+ωττ

⎢⎥

⎣⎦

∫



(25)

The replacement of (25) into (22) yields:

[]

()t t

()

()t ()

e N(t) e E(0) I(0)

R(0) e (1 )I( ) N( )V( ) d

R(0) e h(t) h(0) ( ) e h( )d

μ+ω ω

μ+ω τ

μ+ω μ+ω τ

β−γ

−+

=+ γ−ρτ+ντττ

=+ −−μ+ω ττ

∫

(26)

and equivalently:

[]

()

()t

()(t) t

()(t)

h(t) N(t) e h(0) R(0)

( ) e h( )d e E(0) I(0)

N(t) ( ) e h( )d

e e h(0) R(0) E(0) I(0)

−μ+ω

− μ+ω −τ −μ

− μ+ω −τ

−μ −ω

β−γ

=+ −

+μ+ω τ τ− +

β−γ

=+μ+ω ττ

+−−−

∫

(27)

generated from:

[]

[][]

()t t

2()(t)

h(t) ( )N(t) I(t)

( )e h(0) R(0) e E(0) I(0)

()e h()d()h(t)

−μ+ω −μ

−μ+ω −τ

−

= ν−μ −ργ

−μ+ω − +μ +

− μ+ω τ τ+ μ+ω

∫



(28)

so that:

[][]

()t t

2()(t)

()( )

h(t) (1 )I(t) N(t) 1 I(t)

( )e h(0) R(0) e E(0) I(0)

( ) e h( )d ( )h(t)

−μ+ω −μ

− μ+ω −τ

⎛⎞

β−γ ν−μ γρ

−γ −ρ = +γ −

⎜⎟

ββ

⎝⎠

−μ+ω − +μ +

−μ+ω τ τ+μ+ω

∫



(29)

The vaccination law which ensures the positivity

of the mathematical SEIR-model (1)-(4) is generated

as follows:

[]

V(t) if V(t) 0, 1

V(t) 1 if V(t) 1

0 if V(t) 1

⎧

∈

⎪

⎨

⎪

⎩

(30)

where:

h(t) (1 )I(t)

V(t)

N(t)

−γ −ρ



(31)

Define the indicator function i(t) as follows:

[]

0 if V(t) 0, 1

i(t)

1 otherwise

⎧

∈

⎪

⎨

⎪

⎩

(32)

Then, one has instead of (15):

[

]

S(t) R(t) N(t) E(t) I(t)

S( )

e S(0) R(0) N(0) e I( )i( )d

N( )

S( )

e E(0) I(0) e I( )i( )d

N( )

−μ μτ

+−=− +

⎡

⎤

⎛⎞

+−+ γ−β τττ

⎢

⎥

⎜⎟

⎝⎠

⎣

⎦

⎡⎤

⎛⎞

=− + − γ−β τ τ τ

⎢⎥

⎜⎟

⎝⎠

⎣⎦

∫

(33)

which coincides with (15) for all time if the indicator

function is identically zero, that is, if h(t)



is such

that the auxiliary vaccination law (31) is in

[

]

0, 1

for all time. Also, one gets from (15) that:

(t )

S( )

N(t) S(t) R(t) e I( )i( )d

N( )

−μ −τ

⎛⎞

−

−≤ε+ β −γτττ

⎜⎟

⎝⎠

∫

(34)

1 N(0) S(0) R(0)

tT() ln

−−

⎛⎞

∀≥ ε

⎜⎟

με

⎝⎠

 for any given

real 0

> . The right-hand-side integral of (34) takes

into account the tracking deterioration if there is a

time interval of nonzero Lebesgue measure such that

V(t) V(t)≠

∀∈\ . The following result is

important to discuss stability when the vaccination

law

[

]

V(t) 0, 1∈ but it is not identically equal to

V(t) . In fact, the positivity part of Theorem 1 still

holds because of the SEIR-model is positive since

[

]

V(t) 0, 1∈

∀∈\ and the whole population

evolution is independent of the vaccination law

according to (5). However, the whole susceptible

plus immune does not asymptotically track the

whole population. In summary, one has:

Theorem 3. The vaccination law (28), (30)-(31)

makes the SEIR–model (1)-(4) positive and globally

stable under Theorem 2. Furthermore,

ON VACCINATION CONTROLS FOR THE SEIR EPIDEMIC MODEL WITH SUSCEPTIBLE PLUS IMMUNE

POPULATIONS TRACKING THE WHOLE POPULATION

169

{

}

(t )

lim N(t) S(t) R(t)

S( )

lim sup e I( )i( )d

N( )

→∞

−μ −τ

→∞

−−

⎡⎤

⎛⎞

≤β−γτττ

⎢⎥

⎜⎟

⎝⎠

⎣⎦

∫

***

A more practical vaccination law is defined as

follows:

{

}

{}

aux

min S(t), R(t) 0 and

V(t) if

V(t)

min E(t), I(t) 0

V (t) otherwise

⎧

⎪

⎨

≥

⎨

⎪

⎩

⎪

⎩

(35)

with

V(t) given by (31) and

aux

V (t) obtained from:

aux

1 if S(t) 0 and / or R(t) 0

V(t)

0 otherwise

⎧

⎨

⎩

(36)

Remark 1. The inclusion of the auxiliary function

aux

V (t) in (35) guarantees the non-negativity of the

susceptible and remove-by-immunity populations. In

this sense, note that large values of

V(t) could

eventually do negative S(t) or R(t) from (1)-(4).

This fact is avoided with such a construction of

V(t) since

aux

V(t) V (t)= at the time instants where

S(t) 0= and/or R(t) 0= guarantees that S(t) 0≥



and R(t) 0≥



∀∈\ . Moreover, the non-

negativity for S(t) and R(t) guarantees the non-

negativity of the infected and infectious populations

from (2) and (3). Finally, note that the construction

of the vaccination function (35)-(36) lets that E(t)

and I(t) reach zero, which is the ideal objective for

the eradication of the infection from the population.

In summary, such an alternative control law

guarantees the positivity property for the SEIR-

epidemic model by the proper construction of the

law. In this sense, the condition

[

]

V: 0, 1

→\ in

Theorem 1 is a sufficient, but a non-necessary,

condition to ensure the positivity of the system. ***

4 SIMULATION EXAMPLE

An example based on the rabbit hemorrhagic disease

in United Kingdom is considered to illustrate the

theoretical results presented in the paper. An initial

population of

(0) 1000= rabbits is used. Such an

epidemic can be described by the SEIR model (1)-

(4) with the parameter values:

0.01 per day (p. d.)μ= , 0.017 p. d.ν= ,

0.936 p. d.β= , 0.0333 p. d.ω= ,

0.9314ρ=

and

0.025 p. d.σ=γ= . Such values are commonly used

in the literature (Keeling and Rohani, 2008, White et

al., 2004). The main characteristic of such an

infection is its high mortality, note the value of the

probability of dying from the infection (

0.9314ρ=

)

close to 1. The initial conditions for the individual

populations are given by: S(0) 800= , E(0) 80

I(0) 50

and R(0) 70

The time evolution of the system in the free-

vaccination case, i.e. if V(t) 0=

∀∈\ is

displayed in Figure 1. The population of rabbits

disappears because of the high mortality of the

infection as it can be seen in such a figure. As a

consequence, a vaccination strategy has to be

applied if the persistence of the rabbits is required.

In this sense, Figure 2 displays the evolution of the

total, the susceptible and the removed-by-immunity

populations if the vaccination control law defined by

(28), (31), (35) and (36), with the initial condition

h(0) 0

, is applied. On the other hand, the time

evolution of the infected and the infectious

population with such a vaccination strategy is shown

in Figure 3. The total population of the rabbits

monotonically grows through time as it can be seen

from Figure 2. Moreover, the infected and infectious

population decrease to zero as time grows as it is

seen in Figure 3. In other words, the infection is

eradicated after a time interval and then, the

population of rabbits grows in a fast way, like it

occurs in absence of disease. Finally, the time

evolution of the vaccination function is displayed in

Figure 4.

0 200 400 600 800 1000 1200 1400 1600 1800 2000

200

400

600

800

1000

1200

Time (days)

Total and partial populations

N(t)

S(t)

E(t)

I(t)

R(t)

Figure 1: Time evolution of the total and individual

populations without vaccination.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

170

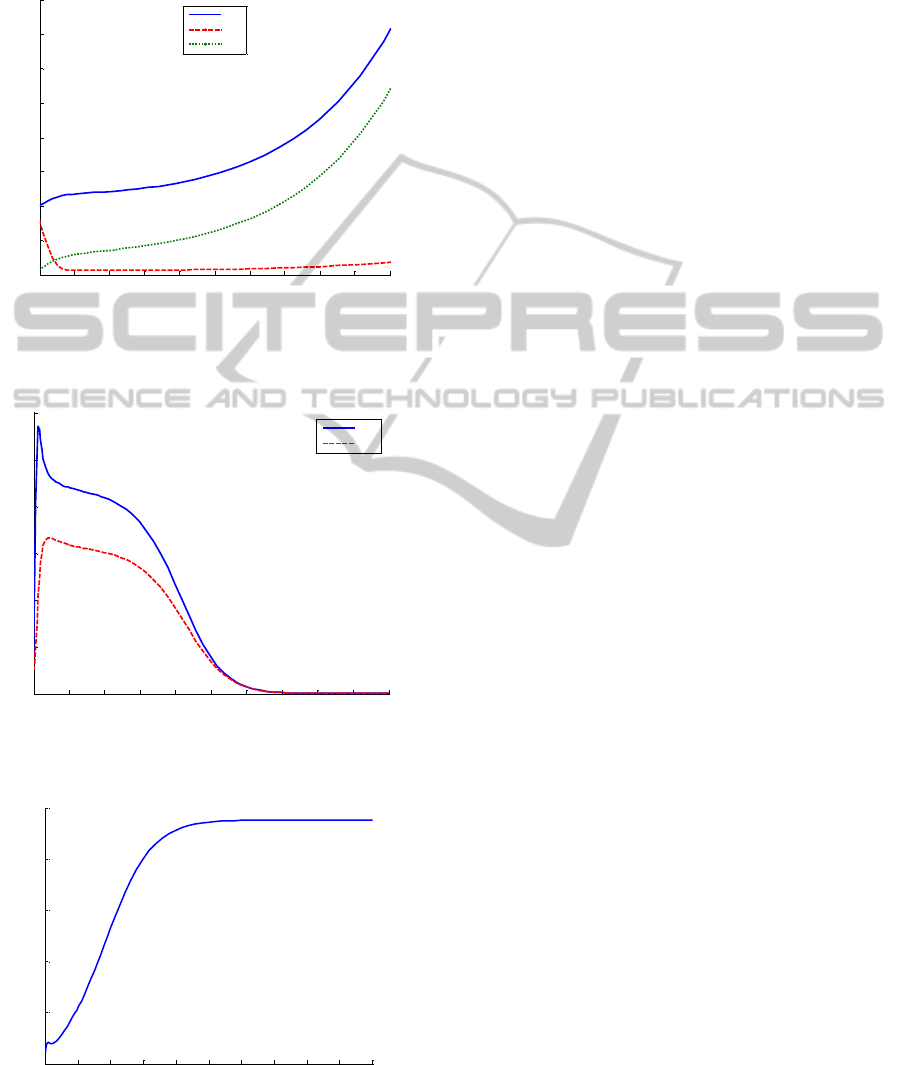
These simulation results point out the improvement

of the use of a vaccination strategy in order to

guarantee the suitable growth of a population against

a high mortality infectious disease.

0 50 100 150 200 250 300 350 400 450 500

500

1000

1500

2000

2500

3000

3500

4000

Time (day s )

Total, susceptible and remove-by-inmmunity populations

N(t)

S(t)

R(t)

Figure 2: Time evolution of the total, susceptible and

removed-by-immunity populations with the proposed

vaccination control law.

0 200 400 600 800 1000 1200 1400 1600 1800 2000

100

200

300

400

500

600

Time (days)

Infected and infectious populations

E(t)

I(t)

Figure 3: Time evolution of the infected and infectious

populations with the proposed vaccination control law.

0 200 400 600 800 1000 1200 1400 1600 1800 2000

0.5

1.5

2.5

Time (days)

Vaccination function

Figure 4: Time evolution of the vaccination associated to

the control law.

5 CONCLUSIONS

A vaccination control strategy has been presented to

eradicate the propagation of infectious diseases. The

SEIR mathematical model has been used to design a

control action via a vaccination strategy, which

modifies suitably the system dynamics in order to

get the disease eradication objective. The

performance of such a vaccination strategy has been

illustrated via some simulation results based on the

rabbit hemorrhagic disease. Such results show that

continuous-time vaccination through the population

could be carried out in order to eradicate the

epidemic

. Otherwise, the rabbits population

extinguishes due to the high mortality associated to

such an epidemic disease.

Future research is in progress to deal with more

general models to describe propagations of diseases.

Also, other types of control strategies based on

impulsive or discrete-time vaccinations are going to

be treated.

ACKNOWLEDGEMENTS

The authors thank to the Spanish Ministry of

Education by its support of this work through Grant

DPI2009-07197 and to the Basque Government by

its support through Grants IT378-10, SAIOTEK

SPE07UN04 and SAIOTEK SPE09UN12.

REFERENCES

De la Sen, M., 2008. About the properties of a modified

generalized Beveron-Holt equation in ecology models.

Discrete Dynamics in Nature and Society 2008,

Article ID 592950, 23 pages, doi:

10.1155/2008/592950.

De la Sen, M., 2008. The generalized Beverton-Holt

equation and the control of populations. Applied

Mathematical Modelling 32, pp. 2312-2328.

De la Sen, M., Alonso-Quesada, S., 2008. A control theory

point of view on Beverton-Holt equation in population

dynamics and some of its generalizations. Applied

Mathematics and Computation 199, pp. 464-481.

De la Sen, M., Alonso-Quesada, S., 2008. Model-

matching-based control of the Beverton-Holt equation

in Ecology. Discrete Dynamics in Nature and Society

2008, Article ID 793512, 21 pages, doi:

10.1155/2008/793512.

De la Sen, M., Alonso-Quesada, S., 2009. Control issues

for the Beverton-Holt equation in ecology by locally

monitoring the environment carrying capacity: Non-

adaptive and adaptive cases. Applied Mathematics and

ON VACCINATION CONTROLS FOR THE SEIR EPIDEMIC MODEL WITH SUSCEPTIBLE PLUS IMMUNE

POPULATIONS TRACKING THE WHOLE POPULATION

171

Computation 215, pp. 2616-2633.

Erturk, V. S., Momani, S., 2008. Solutions to the problem

of prey and predator and the epidemic model via

differential transform method, Kybernetes 37, pp.

1180-1188.

Keeling, M. J., Rohani, P., 2008. Modeling Infectious

Diseases in Humans and Animals, Princeton

University Press, Princeton and Oxford.

Khan, H., Mohapatra, R. N., Varajvelu, K., Liao, S. J.,

2009. The explicit series solution of SIR and SIS

epidemic models. Applied Mathematics and

Computation 215, pp. 653-669.

Mollison, D., 2003. Epidemic Models: Their Structure and

Relation to Data, Publications of the Newton Institute.

Cambridge University Press.

Mukhopadhyay, B., Battacharyya, R., 2007. Existence of

epidemic waves in a disease transmission model with

two-habitat population. International Journal of

Systems Science 38, pp. 699-707.

Ortega, N., Barros, L. C., Massad, E., 2003. Fuzzy gradual

rules in epidemiology. Kybernetes, 32, pp. 460-477.

Song, X. Y., Jiang, Y., Wei, H. M., 2009. Analysis of a

saturation incidence SVEIRS epidemic model with

pulse and two time delays. Applied Mathematics and

Computation 214, pp. 381-390.

White, P. J., Trout, R. C., Moss, S. R., Desai, A., Armesto,

M., Forrester N. L., Gould, E. A., Hudson, P. J., 2004.

Epidemiology of rabbit haemorrhagic disease virus in

the United Kingdom: evidence for seasonal

transmission by both virulent and avirulent modes of

infection. Epidemiology and Infection 132, pp. 555-

567.

Yildirim, A., Cherruault, Y., 2009. Anaytical approximate

solution of a SIR epidemic model with constant

vaccination strategy by homotopy perturbation

method. Kybernetes 38, pp. 1566-1575.

Zhang, T. L., Liu, J. L., Teng, Z. D., 2009. Dynamic

behaviour for a nonautonomous SIRS epidemic model

with distributed delays. Applied Mathematics and

Computation 214, pp. 624-631.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

172