ROBUSTNESS OF EXON CGH ARRAY DESIGNS

Tomasz Gambin

, Pawel Stankiewicz

, Maciej Sykulski

and Anna Gambin

3,4

Institute of Computer Science, Warsaw University of Technology, 15/19 Nowowiejska, 00-665 Warsaw, Poland

Department of Molecular and Human Genetics, Baylor College of Medicine, Houston, U.S.A.

Institute of Informatics, University of Warsaw, 2 Banacha, 02-097 Warsaw, Poland

Mossakowski Medical Research Centre Polish Academy of Sciences, 5 Pawinskiego, 02-106 Warsaw, Poland

Keywords:

aCGH, Segmentation, Noise robustness, Design optimization, DNA copy.

Abstract:

Array-comparative genomic hybridization (aCGH) technology enables rapid, high-resolution analysis of ge-

nomic rearrangements. With the use of it, genome copy number changes and rearrangement breakpoints can

be detected and analyzed at resolutions down to a few kilobases. An exon array CGH approach proposed

recently accurately measures copy-number changes of individual exons in the human genome. The crucial

and highly non-trivial starting task is the design of an array, i.e. the choice of appropriate (multi)set of oligos.

The success of the whole high-level analysis depends on the quality of the design. Also, the comparison of

several alternative designs of array CGH constitutes an important step in development of new diagnostic chip.

In this paper we deal with these two often neglected issues.

We propose new approach to measure the quality of array CGH designs. Our measures reﬂect the robustness of

rearrangements detection to the noise (mostly experimental measurement error). The method is parametrized

by the segmentation algorithm used to identify aberrations. We implemented the efﬁcient Monte Carlo method

for testing noise robustness within DNAcopy procedure. Developed framework has been applied to evaluation

of functional quality of several optimized array designs.

1 INTRODUCTION

DNA copy number aberrations that cause a gain or

loss of chromosomal material are associated with

many types of genomic disorders like mental retar-

dation, congenital malformations or autism (Lupski,

2009; Shaw et al., 2004). Moreover, genetic aber-

rations are characteristic of many cancer types and

are thought to drive some cancer pathogenesis pro-

cess (O’Hagan et al., 2003; Snijders et al., 2005;

Wang et al., 2006; Lai et al., 2007).

Array comparative genomic hybridization

(aCGH) became the standard protocol for identifying

segmental copy number alterations in disease state

genomes (Pollack et al., 1999; Perry et al., 2008).

In typical experiment each DNA (e.g. diseased

patient vs. healthy donor, or normal tissue vs. tumor)

is labeled by different ﬂuorescent dye, and then

hybridized to an array. Signal ﬂuorescent intensities

of each spot from both samples are considered to be

proportional to the amount of respective genomic

sequence present.

One can classify the CGH arrays into two types.

The ﬁrst kind, targeted CGH arrays provide high-

resolution coverage of the genome primarily in areas

containing known, clinically signiﬁcant aberrations,

see e. g. (Thomas et al., 2005; Caserta et al., 2008).

The second kind, whole-genome arrays, provide high

resolution coverage of the entire genome (Barrett

et al., 2004). However in many applications the

design of the array should combine these two ap-

proaches: the exploration of the whole genome with

the special focus on some speciﬁc regions (e.g. con-

taining genes related to the disease under study).

Related Research. The array design is the starting

point of the study on genomic disorders underlying

a given disease (Lemoine et al., 2009). There is a

large body of research concerning array design task,

see e.g. (Lipson et al., 2002; Lipson et al., 2007).

Similarly many papers consider the issues of normal-

ization and detrending array CGH data (Chen et al.,

2008; van Hijum et al., 2008; Staaf et al., 2007; Kreil

and Russell, 2005).

However, while conducting the large-scale

173

Gambin T., Stankiewicz P., Sykulski M. and Gambin A..

ROBUSTNESS OF EXON CGH ARRAY DESIGNS.

DOI: 10.5220/0003153201730182

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 173-182

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

biomedical research projects it is a reasonable

practice to provide several prototype array designs.

A matter of fundamental importance here is how to

compare the functional quality of different arrays

to choose the best one for further experiments.

Moreover, often for this comparison task researchers

dispose of only limited amount of experimental data.

In contrast to array design and normalization stud-

ies, there are only few approaches proposed so far

in the literature to the problem of comparison be-

tween different array designs. There are some stan-

dard statistics calculated for purpose of array com-

parison. They comprise usually: Signal to Noise Ra-

tio, Derivative Log Ratio Standard Deviation, Back-

ground Noise, etc (Carter, 2002). In (Coe et al., 2007)

to compare the resolution of different arrays the new

performance measure called ”functional resolution”

was proposed. This measure incorporates the unifor-

mity of element spacing on the array and the sensitiv-

ity of the array to single-copy alterations.

Our Results. Analogously to other high-

throughput technologies (like mass spectrometry

or expression microarrays) various sources of tech-

nical and biological variation affect the array CGH

experiment. The measurement noise comes from

the preparation of the microarray slide and the

hybridization process, while the biological variability

arises from the heterogeneity of the cells in the

inspected samples (e.g. mosaicism (Iourov et al.,

2008)). However, despite increasing resolution of

CGH arrays the variation in signal measurements

cannot be eliminated. Therefore the methods capable

to detect aberrations even in very noisy data are of

great interest. Most of proposed solutions rely on

so-called segmentation methods that try to divide the

data into segments representing aberrant and normal

regions (Cahan et al., 2008; Daz-Uriarte and Rueda,

2007; Ben-Yaacov and Eldar, 2008; Lipson et al.,

2006).

According to several comparative studies pub-

lished so far (Willenbrock and Fridlyand, 2005) one

of the best performing method for ﬁnding copy num-

ber segments is Circular Binary Segmentation (CBS),

a segmentation approach based on ﬁnding change-

points in data (implemented e.g. in DNAcopy (Olshen

et al., 2004) R package).

Our goal in this study was to develop the frame-

work for performance comparison of different CGH

array designs. We decided to explore the concept of

robustness. The proposed methodology follows the

general concept of robust statistics (Hampel et al.,

2005), quoting B.D. Ripley an important area that is

used a lot less than it ought to be.

In our approach we consider the design robust

when it is effective in the detection of aberrations in

the presence of noise. The segmentation obtained for

the given design is treated here as a robust estimator

of rearrangement regions. Better designs correspond

to more robust estimators, i.e., those approximating

the aberrations for the data contaminated with the

noise. To our best knowledge, this work is the ﬁrst

method that uses the noise sensitivity of segmentation

algorithm to compare different array designs. Aiming

in testing the robustness of a design we enhance the

DNAcopy method by incorporating parametrized

noise model. The R package named DNAcopyNoise

is provided as supplementary material available at

http://bioputer.mimuw.edu.pl/software/DNAcopyNoise.

Our results are twofold: ﬁrstly, using synthetic

data we demonstrate the usefulness of robustness

measure for array performance comparison. Sec-

ondly, we apply the concept of robustness to select

the best one from several optimized designs. The op-

timization aimed in reducing array size while keeping

the same rearrangements detection ability.

Organization of the Paper. Section Methods con-

tains the description of datasets used in our experi-

mental study. We decided to test our method on syn-

thetic datasets representing designs of different qual-

ity. Then we present the 180 K exon array design.

The enhancement of DNAcopy package is presented

and our performance quality measures are deﬁned. In

the Results Section we present the evaluation of our

measure for hybridization experiments and robustness

based comparison of optimized designs. In Conclu-

sions we summarize our approach and sketch further

developments.

2 METHODS

2.1 Synthetic Array Design

Aiming in validation of robustness approach we gen-

erate several datasets using framework from (Willen-

brock and Fridlyand, 2005). Two types of datasets

generators are considered: they correspond to differ-

ent genomic rearrangements structure (high density of

relatively short segments, like in cancer tissues versus

rare long aberrant segments characteristic to genomic

disorders). For each type of data we consider differ-

ent array designs. E.g., for data of ﬁrst type, dataset

(a) presented in Figure 1 is the exemplary output of

aCGH experiments performed on well designed array.

Dataset (b) corresponds to experimental data from the

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

174

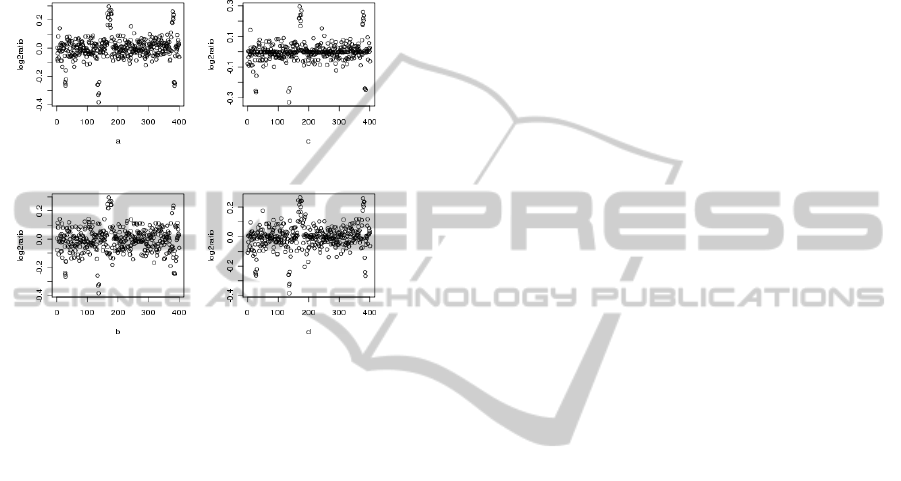
design, in which the inappropriate probe selection re-

sulted in poor hybridization. The generator (b) is ob-

tained as the following modiﬁcation of the original

generator (a). We choose uniformly at random 20

percent of probes and multiply their signal intensity

by the coefﬁcient sampled from beta distribution with

shape parameters α = 2 and β = 20 (unimodal distri-

bution deﬁned on the interval [0, 1]).

Figure 1: Plots show log2ratio (y-axis) vs. genomic location

(x-axis) for synthetic datasets corresponding to four differ-

ent array designs: (a) original datasets, (b) dataset with sim-

ulated poor hybridization effect, (c) dataset with simulated

error-prone analysis procedures, (d) dataset with both ef-

fects.

The generator corresponding to array design (c)

mimics the problems arising from erroneous anal-

ysis protocol that results in signiﬁcant background

noise. We assume here, that some probes may be er-

roneously analysed already during the scanning pro-

cess and only one from Red (cy5) and Green (cy3)

signal is detected. To model such situation we choose

uniformly at random 15% of probes and sample their

intensities from the beta distribution with parameters

α = 0.7 and β = 0.7. Such readouts correspond to

the probe signals not well scattered around zero in the

typical MA plot. The design (d) suffers from both

shortcomings. We generate 40 datasets using each de-

sign. One synthetic genome hybridization experiment

measure the signal intensities of 10000 probes located

on 10 chromosomes.

2.2 Exon CGH Array Design

Our new design quality measure has been tested on

samples obtained in aCGH experiments. The dataset

come from 60 arrays hybridized with DNA from sub-

jects with epilepsy, autism, heart defects and men-

tal disorders. Each experiment was performed on the

180 K exon targeted oligonucleotide array.

Prototype Design. The design of the chip involved

two stages. First, the prototype covering only ex-

onic and microRNA regions was constructed. The

main aim at this stage was to develop the array that

allows detecting DNA copy number changes of the

single exon. Therefore, it was postulated to cover

each exon by the same number of oligos. For a given

set of 1714 selected genes (including those related to

epilepsy, autism, heart defects, mental disorders and

other known pathologies) it was decided that each

exon would be covered by approximately 6 probes.

Cleaning Stage. The prototype coverage was two

times denser than the desired one in the ﬁnal ver-

sion. A set of hybridizations was performed with the

prototype version. Performance score of each probe

was computed as following: segmentation was per-

formed on data from these experiments. Let us call

the empirical cumulative distribution function for dis-

tribution of logratios deviations from their segments

means F . The distribution F was estimated from

all experiments from the prototype version. For each

probe we perform two sided Kolomogorov-Smirnov

(K-S) test comparing the logratio deviation from seg-

ment mean with distribution F . We assign the p-value

obtained in this test as a score of the probe.

Next step involved combining the prototype de-

sign with backbone, i.e., probes putted uniformly

across the genome. Densely covered regions, ex-

onic double covered regions were thinned with heuris-

tic approach which considered previously assigned

scores and uniformity of nascent coverage (sizes of

introduced gaps).

2.3 Enhancement of DNACopy

DNAcopy package for R environment implements

circular binary segmentation algorithm (Olshen et al.,

2004). CBS algorithm ﬁnds segmentation by recur-

sively splitting subsequent segments into three, or two

smaller ones. Each segment cut is found by maximiz-

ing the following statistic:

= max

1≤i< j≤n



i j



(1)

where t

i j

is t-statistic for probes resulting from parti-

tion of the cyclic logratio series at points i, j into two

samples: probes inside the interval (i,j), and its com-

plement.

Segmentation proceeds when the null hypothesis

is rejected, that is when Z

is above upper α−quantile

of null distribution Z

∗

ROBUSTNESS OF EXON CGH ARRAY DESIGNS

175

CBS algorithm estimates the null distribution with

the use of permutation method and tail probability es-

timation.

To estimate robustness of a segment we introduce

a Gaussian noise to the logratio data. We are inter-

ested in ﬁnding minimal level of noise that is very

likely to make the considered segment undetectable,

i.e., the maximal level that still guarantees that seg-

ment persists. Detecting these numbers through sim-

ulation requires extensive sampling since the intro-

duced noise is highly dimensional random variable.

To avoid running CBS algorithm many times, we in-

troduced the noise inside the sampling phase. CBS

use sampling to estimate the null distribution, by per-

mutation method. In our algorithm, every permuta-

tion is sampled with random noise added with zero

mean and η standard deviation. This changes the Z

∗

distribution and the sought quantile. This is com-

pared with the previously computed, however scaled

accordingly to introduced noise variance, t

i j

statistic

for the analyzed segment.

By tuning CBS parameters, speciﬁcally by, in-

creasing the number of permutations in each step, the

answer we obtain (if the segment is detectable with in-

troduced noise level η) is statistically signiﬁcant. To

assign η

to each aberrant segment k we follow the

original, not noisy, CBS segmentation sequence, and

introduce noise in binary search fashion up to desired

precision.

2.4 Robustness Measure

It is inevitable that the measurement precision vary

considerably between probes depending on the hy-

bridization efﬁciency. Hence some regions of the

genome are analyzed with signiﬁcantly higher preci-

sion than others (Baldocchi et al., 2005). Therefore

it is desirable to model the effectiveness of speciﬁc

array region in detecting aberrations. We propose an

approach that allows to evaluate the quality measure

for a whole array but also to focus on speciﬁc set

of probes. In our method we measure the quality of

array design using noise robustness of segmentation

algorithm performed for all accessible aCGH experi-

ments.

The intuition behind this approach can be ex-

plained in simple terms. Segmentation algorithm pro-

vides the information about comparative hybridiza-

tion experiment. Aberrant segments are easily de-

tectable if they are represented by good quality

probes. Good probes should tolerate higher level of

measurement noise than poor quality probes. There-

fore we conduct segmentation procedure for several

increasing noise levels and observe the behavior of

aberrant segments. There is certain number of seg-

ments found for original experimental data. Then

we simulate some measurement noise and repeat seg-

mentation algorithm. Some segments (consisted of

poor quality probes) disappear and we continue this

process, memorizing for each segment the maximal

noise level, for which this segment is still identiﬁ-

able (for a ﬁxed segment k we denote this value by

). The output of several segmentation stages for 2

different (synthetic) designs is presented in Figure 2.

Clearly, the left panel corresponds to more robust de-

sign.

Let us ﬁx the aCGH experiment and let η

denote

the noise level of the maximal noise resistance of kth

segment deﬁned as above. The level of noise is mea-

sured with reference to baseline variation (standard

deviation of probes in non aberrant regions). The ro-

bustness of probe k is deﬁned as:

length(k) · |mean(k)|

(2)

where length(k) is the length of segment k (measured

in the number of probes), and |mean(k)| is the abso-

lute value of mean of signal intensities along the seg-

ment. We assign the segment robustness to all the

probes it contains.

Now we combine the segmentation robustness of

several aCGH experiments into the measure of array

design quality. The robustness score for an array is

composed from robustness of probes it consists of.

Note that, we can estimate the quality only for those

probes that are witnesses of some aberration. Con-

sider a single probe k and assume, that it belongs to

aberrant segment in some samples (according to seg-

mentation algorithm run for original data). To this

probe robustness scores θ

, θ

, . . . θ

have been as-

signed in experiments i

, . . . i

. Assume, that there are

m accessible experiments in total. As an overall qual-

ity of this probe we can take the median of the empir-

ical distribution of robustness scores θ

, θ

, . . . θ

However in the case of limited number of acces-

sible experimental data we encounter here the prob-

lem of insufﬁcient statistic, because a single probe

can be the witness of only few aberrations. To avoid

this difﬁculty we apply the sliding window approach.

The empirical distribution of probe robustness is com-

posed for all probes contained in the window of pre-

deﬁned length n (depending on the resolution of an

array). The median of this distribution is calculated

yielding the smoothed version of the overall probe

quality.

The next neighboring window is shifted by the

half of the window length. Therefore any single

probe contributes to exactly two window statistics

(the boundary probes are ignored). Assume that the

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

176

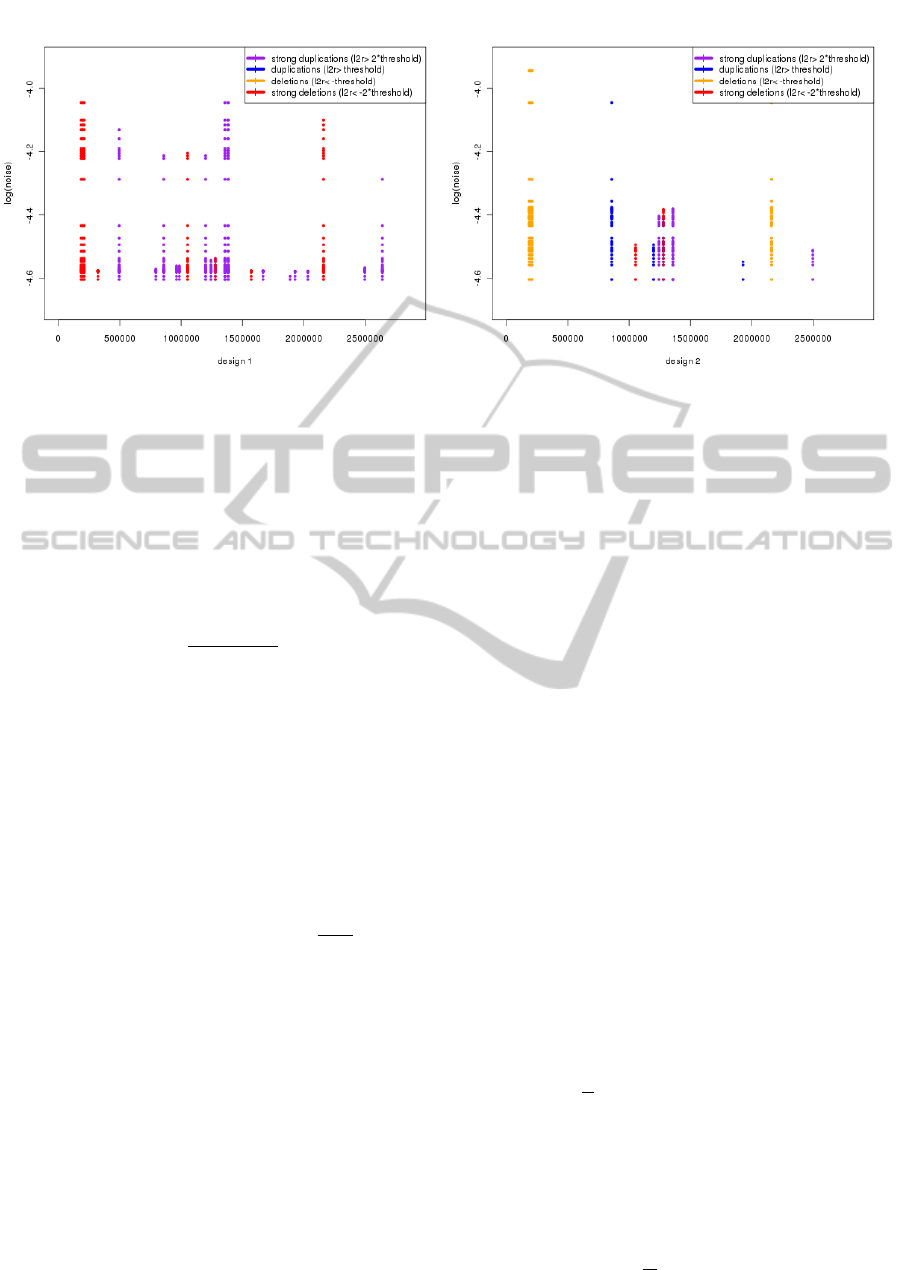
Figure 2: The resistance of aberrant segments for increasing noise. y-axis correspond to increasing noise level (logarithmized),

different segments are placed along x-axis (genomic location), the logratios are color-coded.

median (µ

) from the ﬁrst window is calculated for i

events (aCGH experiments in which this probe lies in

the aberrant segment) and the second µ

for i

events.

Then the ith probe robustness for the array A is de-

ﬁned as:

+ i

(3)

The robustness of array design A (containing N

probes) can be calculated by taking the average ro-

bustness of all probes.

However, the important issue here is that the cal-

culation of robustness for some probes relies on many

detected aberrations containing this probe, while for

others the robustness measure is supported by only

few witnesses. Consider once more the probe i and

two windows containing it. A support for the ith

probe robustness Θ

is deﬁned as s

i.e., the

percent of experiments in which this probe or its sur-

rounding probes are witnesses of some aberration.

The support vector is composed of all probe sup-

ports s

= s

, . . . , s

. This vector is further

transformed into importance weights vector ω

, . . . , ω

by appropriate normalization and scaling

(the scaling function ﬂatten out the support vector, as

higher support values have roughly the same impact).

Finally, the robustness of array design A is deﬁned as:

= Σ

(4)

In the next Section plots illustrating the robustness for

all probes use logarithmic scale for Θ

2.5 Optimizing Exon CGH Array

Design via Relative Robustness

The robustness measure Θ

deﬁned for a given ar-

ray design A allows to estimate the functional per-

formance of A i.e., the efﬁciency of rearrangements

detection for noisy data. In this section we study the

problem of array design optimization. Our goal is to

eliminate certain percent of probes to obtain smaller

design which has comparable performance.

Here we assume that the segmentation Π found

for the original design reﬂects the real genomic aber-

rations. We refer to segmentation Π while measuring

the robustness of smaller designs. We compare the

optimized array with the original one looking at its

segmentation’s evolution for increasing noise level.

Let us ﬁx the noise level η and deﬁne the distance

between two segmentations (say the original Π and

another one Π

) σ

(Π, Π

) similarly to raw distance

in (Liu et al., 2006), i.e., if both samples have a gain

(or loss) at the same genomic interval τ we consider

them identical, otherwise this genomic interval con-

tributes to the total distance. The contribution from

single interval is deﬁned as its length (measured in

nucleotides) divided by the length of whole genome

(Γ), i.e.:

(Π, Π

) =

∑

τ:τ differs between Π and Π

length(τ) (5)

To calculate the total distance σ

tot

we sum up the

contributions for all genomic intervals that differ be-

tween two samples and take the average over all m

experiments.

tot

∑

i=1

(Π, Π

) (6)

ROBUSTNESS OF EXON CGH ARRAY DESIGNS

177

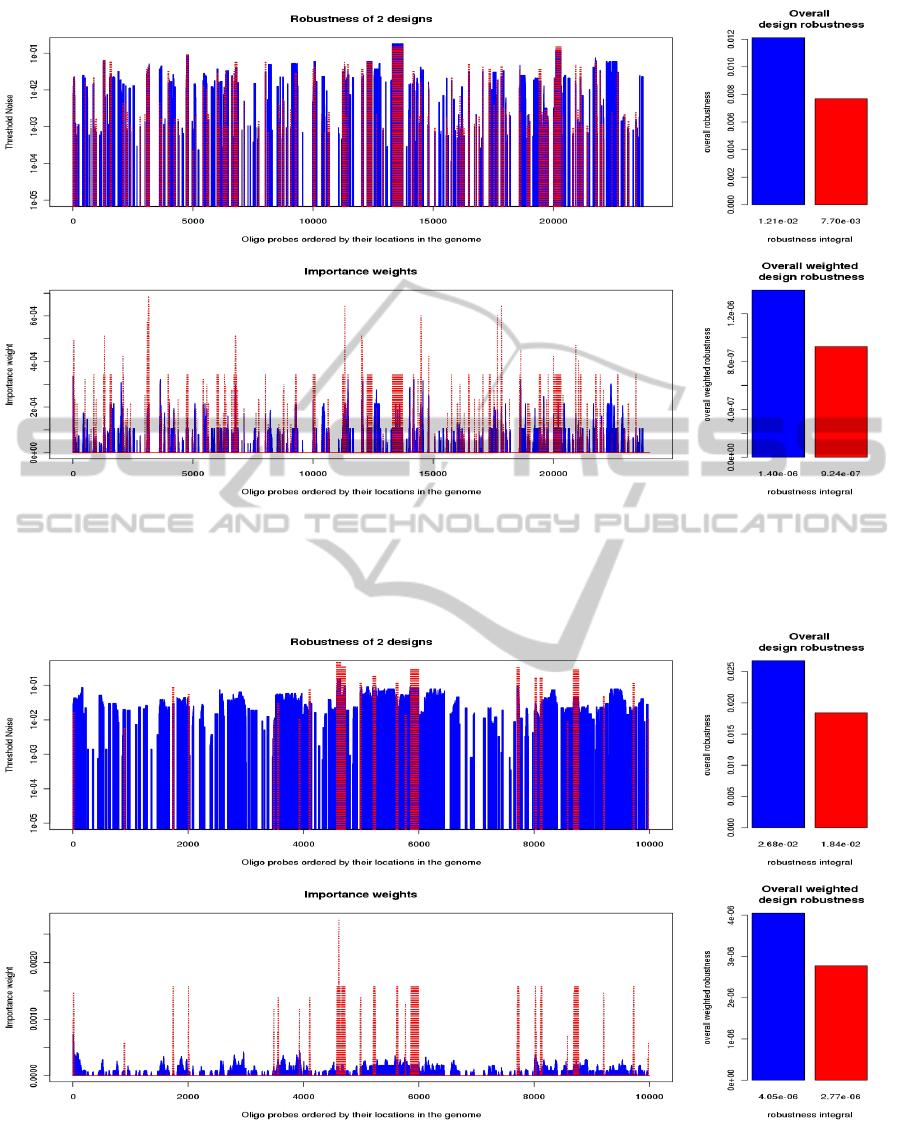
Figure 3: The robustness compared for two synthetic designs. The robustness has been calculated for all probes (upper plot)

as well as corresponding weights importance (lower plot). The structure of genomic rearrangements mimics the abnormalities

in cancer cells. Good design is coded in blue. Red design contains 20% of poorly hybridizing probes and 15% of outliers

(probes causing erroneous scanning).

Figure 4: The robustness compared for two synthetic designs. The robustness has been calculated for all probes (upper plot)

as well as corresponding weights importance (lower plot). The structure of genomic rearrangements mimics the abnormalities

in classical genetic disorder (relatively rare long aberrant segments). Good design is coded in blue. Red design contains 15%

of outliers (probes causing erroneous scanning).

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

178

Figure 5: Comparison of segmentations on optimized and original designs. Figure (a) shows the part of logratio data (1000

oligos on chr 15 - x-axis) obtained in 60 aCGH experiments (y-axis). There can be seen some common copy number changes

for all experiments (probably CNV’s), e.g., small duplications near oligo 600-th (red and yellow vertical line), and larger

deletions near 800-th (blue vertical line). On the Figure (b) we present the p-values from K-S tests performed for each oligo

on original design. For each probe three tests were done, which refer to the goodness of ﬁt of oligo in case it is included

in normal, deleted or duplicated segment. These p-values were then used to prepare optimized designs. Figure (c) refers to

the segmentations on the original design. Figures (d), (e), (f) show the results of segmentations performed on the optimized

(reduced) designs. Segmentations on the Figure (d) come from reduced design, that was obtained by uniform removing

random probes from original one. Segmentations on the Figure (e) come from reduced design, that was obtained by uniform

removing most deviated (from segment mean) oligos (lowest p-values from K-S tests). Segmentations on the Figure (f) come

from reduced design, that was obtained by uniform removing least deviated (from segment mean) oligos (highest p-values

from K-S tests).

Summarizing, the robustness measure used in the

optimization context called relative robustness of

smaller array design A with respect to original one

O is deﬁned as follows:

A|O

max

∑

η=η

min

tot

(7)

ROBUSTNESS OF EXON CGH ARRAY DESIGNS

179

The optimization procedure were preceded by cal-

culation of per-oligo quality score. For each probe in

original design we computed, cumulative properties,

which reﬂects the oligo suitability in the context of its

surrounding. For a given oligo the K-S tests were per-

formed, which compare the distribution of this oligo

logratio deviations to the distribution of logratio de-

viations taken from the neighborhood of this probe.

The KS-test were performed separately for logratio

assigned to duplicated, deleted and non-aberrated re-

gions. As a result, we obtained three p-values, that

describe the probe functional performance (see Fig-

ure 5b). Those p-values were then used to prepare

optimized designs. Details are presented in Results

Section.

3 RESULTS AND DISCUSSION

3.1 Synthetic Data

Figure 3 presents the comparison of two designs eval-

uated on (synthetic) samples characterized by many

relatively short segments (like in cancer tissues). The

blue color corresponds to good design. Weaker de-

sign (coded in red) contains 20% of poorly hybridiz-

ing probes and 15% of outliers. Hence it corresponds

to generator (d) from the previous Section.

For all oligo probes we present their robustness

(upper plot) in logarithmic scale and correspond-

ing importance weights vector ω

(lower plot). It

is clearly visible, that the robustness is signiﬁcantly

higher for better (blue) design.

The evaluation of two other designs tested on typ-

ical genomic disorder (not cancer) datasets is illus-

trated in Figure 4. Blue color codes the outcome for

good design and red color corresponds to design con-

taining 15% of poor probes (yielding logratio read-

outs classiﬁed as outliers), i. e. datasets from this

design are obtained from generator of type (c). Anal-

ogously as for previous example, the better design

yields higher array robustness.

3.2 Testing Robustness of Optimized

Designs

In previous sections we have shown, that robustness

measure can be useful for estimation of the design

performance in detecting aberrated regions. Below

we present several approaches to aCGH design opti-

mization and the application of robustness in evalua-

tion of those designs quality.

Optimized designs were prepared, based on the

data from 60 aCGH experiments, performed on the

180 K array. The goal was to select 80% of oligos

from original design and keep the ability to detect all

aberrated segments.

Note that our approach operates on different level

of abstraction than those presented in (Xia et al.,

2010) where the probe design factor where calculated.

In our study the research focus is on the functional

performance, i.e., the ability of recovering the real

segmentation.

To investigate the inﬂuence of design optimization

strategy on relative array design robustness several

approaches for probes selection were tested, includ-

ing uniform sampling (A

design) and most/least suit-

able oligo removal (A

and A

respectively). Some of

those methods reduced the number of probes with a

little loss of relative robustness. One can beneﬁt from

this strategy especially for targeted arrays used for the

diagnosis of speciﬁc chromosomal aberrations.

The comparison shown on the Figure 5 of three

optimized designs to the original one revealed that

segmentations presented on the Figure 5e are the clos-

est to the segmentations on original design - Fig-

ure 5c. Moreover, segmentations on the Figure 5e,

thanks to removing the worst performing probes, de-

tects more aberrations than it is shown on Figure 5c

(see area near oligos 600-th and 800-th).

On the Figure 6 we present the comparison of rel-

ative robustness Θ

for three different optimized

designs A

, i = 1, 2, 3 with respect to the original de-

sign O. On the y-axis the distance σ

tot

to the original

segmentation Π is shown, while x-axis presents the

increasing value of noise η.

It is clear that for low values of noise segmen-

tation from optimized and original designs are simi-

lar, which implies the small distance between them.

When the noise is higher, then some of the segments,

that were detected before, disappear. In consequence

the distances between segmentations are growing.

From the Figure 6 we can observe that the de-

sign, obtained by removing most deviated oligos, has

the largest relative robustness (keep the smallest dis-

tance to original segmentation while increasing noise

value).

4 CONCLUSIONS

In this paper we introduced new measures for qual-

ity of CGH array performance. In contrast to previ-

ously proposed approaches we focus on the noise ro-

bustness of segmentation procedure. The method is

tested using appropriately enhanced DNACopy seg-

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

180

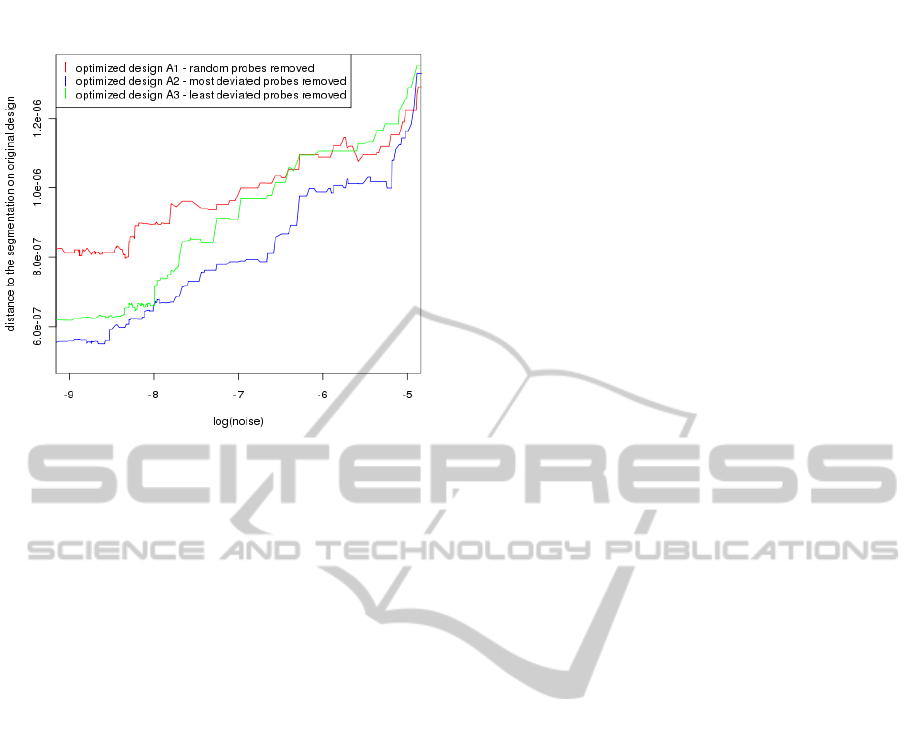
Figure 6: Comparison of relative robustness Θ

for three

optimized designs.

mentation algorithm (Olshen et al., 2004). Our exper-

iments on real datasets justify the applicability of the

robustness approach. Besides the estimation of the

array performance quality we propose the method to

reduce the array size while keeping its quality on the

reasonable level.

The investigation shows that while optimizing the

design it is crucial to ﬁnd a tradeoff between keeping

uniform distribution and selecting the best performing

probes. We discovered that the results of design com-

parisons greatly depends on the deﬁnition of distance

between two segmentations. Finally, we found new

measure of relative robustness very useful for evalu-

ation of optimized design performance in rearrange-

ments detection.

Several improvements are possible. The chal-

lenging problem is whether DNAcopy segmenta-

tion method may be replaced by more efﬁcient one

(e.g. new segmentation method based on a wavelet

decomposition (Ben-Yaacov and Eldar, 2008)). Also

the noise model used in testing the robustness could

better reﬂect the real experimental problems.

Authors Contributions. TG, MS and PS designed

the 180 K exon array. TG and MS implemented pro-

grams and carried out the experiments. TG, MS and

AG led the analysis of the experimental results. AG

and PS inspired the robustness approach and super-

vised the project. All authors contributed to the writ-

ing of this manuscript, and have read and approved

the ﬁnal manuscript.

ACKNOWLEDGEMENTS

This research is supported in part by Polish Ministry

of Science and Educations grants N301 065236, N206

356036 and R13 0005 04. It was also supported by

the Foundation for Polish Science and the European

Social Fund and the State Budget from the Integrated

Regional Operational Program, Action 2.6 ”Regional

Innovation Strategies and Knowledge Transfer”, the

project of Mazovia Voivodship ”Mazovia Doctoral

Scholarship”.

REFERENCES

Baldocchi, R. A., Glynne, R. J., Chin, K., Kowbel, D.,

Collins, C., Mack, D. H., and Gray, J. W. (2005). De-

sign considerations for array CGH to oligonucleotide

arrays. Cytometry. Part A: The Journal of the Inter-

national Society for Analytical Cytology, 67(2):129–

136.

Barrett, M. T., Scheffer, A., Ben-Dor, A., Sampas, N., Lip-

son, D., Kincaid, R., Tsang, P., Curry, B., Baird, K.,

Meltzer, P. S., Yakhini, Z., Bruhn, L., and Laderman,

S. (2004). Comparative genomic hybridization using

oligonucleotide microarrays and total genomic DNA.

Proceedings of the National Academy of Sciences of

the United States of America, 101(51):1776517770.

Ben-Yaacov, E. and Eldar, Y. C. (2008). A fast and ﬂexible

method for the segmentation of aCGH data. Bioinfor-

matics (Oxford, England), 24(16):i139–145.

Cahan, P., Godfrey, L. E., Eis, P. S., Richmond, T. A.,

Selzer, R. R., Brent, M., McLeod, H. L., Ley, T. J.,

and Graubert, T. A. (2008). wuHMM: a robust al-

gorithm to detect DNA copy number variation using

long oligonucleotide microarray data. Nucleic Acids

Research, 36(7):e41.

Carter (2002). Comparative analysis of comparative ge-

nomic hybridization micro array technologies: report

of a workshop sponsored by the wellcome trust. Cy-

tometry, 49(2):43–48.

Caserta, D., Benkhalifa, M., Baldi, M., Fiorentino, F., Qum-

siyeh, M., and Moscarini, M. (2008). Genome pro-

ﬁling of ovarian adenocarcinomas using pangenomic

BACs microarray comparative genomic hybridization.

Molecular Cytogenetics, 1:10.

Chen, H. H., Hsu, F., Jiang, Y., Tsai, M., Yang, P., Meltzer,

P. S., Chuang, E. Y., and Chen, Y. (2008). A probe-

density-based analysis method for array CGH data:

sim ulation, normalization and centralization. Bioin-

formatics (Oxford, England), 24(16):1749–1756.

Coe, B. P., Ylstra, B., Carvalho, B., Meijer, G. A.,

Macaulay, C., and Lam, W. L. (2007). Resolving the

resolution of array CGH. Genomics, 89(5):647–653.

Daz-Uriarte, R. and Rueda, O. M. (2007). ADaCGH: a par-

allelized web-based application and r package for the

analysis of aCGH data. PloS One, 2(1):e737.

ROBUSTNESS OF EXON CGH ARRAY DESIGNS

181

Hampel, F. R., Ronchetti, E. M., Rousseeuw, P. J., and Sta-

hel, W. A. (2005). Robust Statistics: The Approach

Based on Inﬂuence Functions. Wiley Series in Proba-

bility and Statistics.

Hijum, S. A. F. T. V., Baerends, R. J. S., Zomer, A. L.,

Karsens, H. A., Martin-Requena, V., Trelles, O., Kok,

J., and Kuipers, O. P. (2008). Supervised lowess

normalization of comparative genome hybridization

data–application to lactococcal strain comparisons.

BMC Bioinformatics, 9:93.

Iourov, I. Y., Vorsanova, S. G., and Yurov, Y. B. (2008).

Chromosomal mosaicism goes global. Molecular Cy-

togenetics, 1:26.

Kreil, D. P. and Russell, R. R. (2005). There is no silver

bullet–a guide to low-level data transforms and nor-

malisation methods for microarray data. Brieﬁngs in

Bioinformatics, 6(1):86–97.

Lai, C., Horlings, H. M., de Vijver, M. J. V., Beers, E. H. V.,

Nederlof, P. M., Wessels, L. F., and Reinders, M. J.

(2007). SIRAC: supervised identiﬁcation of regions

of aberration in aCGH datasets. BMC Bioinformatics,

8:422.

Lemoine, S., Combes, F., and Crom, S. L. (2009). An evalu-

ation of custom microarray applications: the oligonu-

cleotide design challenge. Nucleic Acids Research,

37(6):17261739.

Lipson, D., Aumann, Y., Ben-Dor, A., Linial, N., and

Yakhini, Z. (2006). Efﬁcient calculation of interval

scores for DNA copy number data analysis. Journal of

Computational Biology: A Journal of Computational

Molecular Cell Biology, 13(2):215–228.

Lipson, D., Webb, P., and Yakhini, Z. (2002). Designing

speciﬁc oligonucleotide probes for the entire s. cere-

visiae transcriptome. Algorithms in Bioinformatics,

pages 491–505.

Lipson, D., Yakhini, Z., and Aumann, Y. (2007). Optimiza-

tion of probe coverage for high-resolution oligonu-

cleotide acgh. Bioinformatics, 23:e77–83.

Liu, J., Mohammed, J., Carter, J., Ranka, S., Kahveci, T.,

and Baudis, M. (2006). Distance-based clustering of

CGH data. Bioinformatics, 22(16):1971–1978.

Lupski, J. R. (2009). Genomic disorders ten years on.

Genome Medicine, 1(4):42.

O’Hagan, R. C., Brennan, C. W., Strahs, A., Zhang, X.,

Kannan, K., Donovan, M., Cauwels, C., Sharpless,

N. E., Wong, W. H., and Chin, L. (2003). Array

comparative genome hybridization for tumor classiﬁ-

cation and gene discovery in mouse models of malig-

nant melanoma. Cancer Res, 63:5352–5356.

Olshen, A. B., Venkatraman, E. S., Lucito, R., and Wigler,

M. (2004). Circular binary segmentation for the analy-

sis of array-based dna copy number data. Biostatistics

(Oxford, England), 5:557–72.

Perry, G. H., Ben-Dor, A., Tsalenko, A., Sampas, N.,

Rodriguez-Revenga, L., Tran, C. W., Scheffer, A.,

Steinfeld, I., Tsang, P., Yamada, N. A., Park, H. S.,

Kim, J.-I., Seo, J.-S., Yakhini, Z., Laderman, S.,

Bruhn, L., and Lee, C. (2008). The ﬁne-scale and

complex architecture of human copy-number varia-

tion. American journal of human genetics, 82:685–95.

Pollack, J. R., Perou, C. M., Alizadeh, A. A., Eisen, M. B.,

Pergamenschikov, A., Williams, C. F., Jeffrey, S. S.,

Botstein, D., and Brown, P. O. (1999). Genome-wide

analysis of dna copy-number changes using cdna mi-

croarrays. Nature genetics, 23:41–6.

Shaw, C. J., Shaw, C. A., Yu, W., Stankiewicz, P., White,

L. D., Beaudet, A. L., and Lupski, J. R. (2004). Com-

parative genomic hybridisation using a proximal 17p

bac/pac array detects rearrangements responsible for

four genomic disorders. J Med Genet, 41:113–119.

Snijders, A. M., Schmidt, B. L., Fridlyand, J., Dekker, N.,

Pinkel, D., Jordan, R. C. K., and Albertson, D. G.

(2005). Rare amplicons implicate frequent deregula-

tion of cell fate speciﬁcation pathways in oral squa-

mous cell carcinoma. Oncogene, 24:4232–42.

Staaf, J., Jonsson, G., Ringner, M., and Vallon-Christersson,

J. (2007). Normalization of array-cgh data: inﬂuence

of copy number imbalances. BMC Genomics, 8:382.

Thomas, R., Scott, A., Langford, C. F., Fosmire, S. P.,

Jubala, C. M., Lorentzen, T. D., Hitte, C., Karls-

son, E. K., Kirkness, E., Ostrander, E. A., Galibert,

F., Lindblad-Toh, K., Modiano, J. F., and Breen, M.

(2005). Construction of a 2-Mb resolution BAC mi-

croarray for CGH analysis of canine tumors. Genome

Research, 15(12):18311837.

Wang, Y., Makedon, F., and Pearlman, J. (2006). Tumor

classiﬁcation based on dna copy number aberrations

determined using snp arrays. Oncology reports, 15

Spec no.:1057–9.

Willenbrock, H. and Fridlyand, J. (2005). A comparison

study: applying segmentation to array cgh data for

downstream analyses. Bioinformatics, 21:4084–4091.

Xia, X.-Q., Jia, Z., Porwollik, S., Long, F., Hoemme, C.,

Ye, K., Muller-Tidow, C., McClelland, M., and Wang,

Y. (2010). Evaluating oligonucleotide properties for

DNA microarray probe design. Nucl. Acids Res.,

38(11):e121.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

182