AUTOMATIC SEGMENTATION OF CONDUCTIVITY CHANGES

IN ELECTRICAL IMPEDANCE TOMOGRAPHY IMAGES

A. Zifan, P. Liatsis, P. Kantartzis and R. Vargas-Canas

School of Engineering and Mathematical Sciences, City University, London, U.K.

Keywords: Electrical impedance tomography, Mesh, Probabilistic modeling and segmentation.

Abstract: In this paper, we propose a novel method for the automatic segmentation of Electrical Impedance

Tomography (EIT) lung images. EIT is a non-invasive technique, which produces low-spatial and high-

temporal resolution images of the internal resistivity of the region of the body probed by currents. EIT is the

only technology that reliably quantifies regional lung volumes non-invasively. The problem is non-linear

and ill-conditioned and can be solved using 2D or 3D finite element methods (FEMs) subject to using

appropriate regularisation strategies. The usual method of segmenting EIT lung images is to manually select

a region of interest and derive statistical measures. This procedure is not suitable for FEM-based models as

it works on rectangular pixels, as well as making the task tedious and time consuming. We propose an

alternative segmentation framework, which operates directly on the resulting FEM meshes, prior to

rasterisation in order to prevent the propagation of errors in the reconstructed resistivity regions, due to

mapping onto a rectangular grid. We use a spatio-temporal probabilistic method to segment conductivity

changes in the EIT thorax images. Application of the proposed method offers a much needed alternative to

interactive segmentation currently favoured by EIT researchers and clinicians.

1 INTRODUCTION

EIT is a non-invasive technique, which produces

images of the internal conductivity or resistivity of

the region of the body probed by alternating currents

(Brown, 2003). EIT could be applied to imaging

both structural and functional abnormalities in the

human lungs. It has several advantages over existing

chest-imaging techniques, including low cost,

portability, its non-invasive and non-ionizing nature,

the potential for ambulatory or ICU measurements

and fast acquisition speed. EIT is the only non-

invasive technique that provides insight into the

regional distribution of ventilation. Current

strategies to provide lung protective ventilation rely

on avoiding lung over distension by reducing tidal

volumes and on opening atelectasis by applying

adequate positive end-expiratory pressure. However,

it is currently impossible to continuously measure

regional lung over distension and atelectasis while a

patient is ventilated, but it would be extremely

relevant information that could lead to reducing

ventilator-induced lung injury. EIT can resolve

changes in the distribution of lung volumes between

dependent and non-dependent lung regions as

ventilator parameters change. Thus, EIT

measurements may be used to control the specific

ventilator settings to maintain lung protective

ventilation on an individual patient basis (Frerichs et

al, 2006).

In EIT, current density flow within the body is

described by Maxwell’s equations. Typically,

multiple electrodes are placed on a person's thorax

and a sinusoidal current excitation is imposed. The

governing equation for the voltage field produced by

placing a current across a material is

()0

ωε ϕ

∇

⋅+ ∇=

(1)

which is an elliptic partial differential equation,

where σ is the electric impedance of the medium, φ

is the electric potential, ω is the frequency, and ε is

the electric permittivity (Molinari, 2003). Equation

(1) is reduced to the standard governing equation for

EIT

, ()0

∇

⋅∇ = when the angular frequency is

sufficiently low or direct current is used.

By repeating these steps and scanning around

various electrode pairs, it is possible to calculate the

approximate current distribution inside the body

through inverse solution of Maxwell's equations

using two or three-dimensional finite element

215

Zifan A., Liatsis P., Kantartzis P. and Vargas-Canas R..

AUTOMATIC SEGMENTATION OF CONDUCTIVITY CHANGES IN ELECTRICAL IMPEDANCE TOMOGRAPHY IMAGES.

DOI: 10.5220/0003157002150220

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 215-220

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

methods. A medical image can then be

reconstructed, since the structures within the human

body have different resistivities. However, this

requires the solution of a non-linear, ill-conditioned

inverse problem. The non-linearity arises in σ, since

the potential distribution. φ, is a function of the

impedance, φ= φ(σ), and the ill-conditioning stems

from the fact that small errors in the measurements

or in the forward modelling step may introduce large

errors in the reconstruction. The forward problem in

EIT is to estimate the induced electrical

measurements at the electrodes, given an excitation

signal and permittivity distribution. The inverse

problem estimates the permittivity distribution based

on the excitation signal and the terminal electrical

measurements. Once images have been

reconstructed, following regularization of the

inverse problem, in the final stage, FEM

triangulation results are rasterised to cover a

rectangular grid for subsequent image processing.

2 EIT LUNG IMAGES

2.1 Low Spatial Resolution of EIT

Images

It is well known that a reconstructed EIT image is

unique for noise-free complete boundary data

(Sylvester and Uhlmann, 1986). However, in

comparison to magnetic resonance imaging (MRI)

and computed tomography (CT), EIT suffers from

poor spatial resolution due to noise, low sensitivity

of boundary voltages to inner conductivity

perturbations and a limited number of boundary

voltage measurements (Clay and Ferree , 2002).

Moreover, the reconstructed images are usually

subtracted from a reference frame in order to

minimize errors due to electrode movement or

unknown boundary shape. A comparison of an EIT

image and its CT counterpart of the thorax is shown

in Figure 1. In spite of the above, EIT is very useful

in monitoring patient lung volume, because the air

has a large conductivity contrast compared to other

tissues in the thorax. The large change in lung

impedance with respiration, and the ease of use of

impedance tomography as a monitoring technique,

has led to a significant body of research in lung

impedance (Frerichs, 2000). However, the spatial

resolution of the EIT images reduces further with the

rasterisation process, where FEM model results are

mapped onto a rectangular grid for further image

processing. This rasterisation step introduces further

fuzziness to the reconstructed regions of

conductivity changes in the EIT images of the lungs,

and makes it even harder to determine the outline of

these rapidly changing regions during the breathing

cycle.

(a) (b)

Figure 1: (a) CT image of the thorax (Ackermann, 1995)

(b) EIT difference image (brighter regions correspond to

larger conductivity changes).

2.2 Feasibility of EIT Image

Segmentation

Due to the aforementioned problems regarding the

poor spatial resolution of EIT images, a question

arises as to whether it is possible to introduce a

robust adaptive EIT segmentation method.

Currently, there exists no method, which could

automatically segment regions with significant

conductivity changes, corresponding to the lobes for

an entire EIT breathing cycle sequence. The usual

method of segmenting or interrogating images is to

select a region of interest (a pixel or a small region)

on the image and then derive statistical measures for

the selected regions (Smallwood, 1999).

An additional problem is that EIT patient

histories generally include data from a limited

battery of tests, thus, making it difficult to train a

sufficiently complete probabilistic model.

Traditional background subtraction algorithms are

not appropriate due to the slower inflation/ deflation

rate of the lungs compared to the acquisition frame

rate (i.e., 13 fps), hence changes in the lung lobe

conductivity images appear slow moving or

temporarily stationary. Under these conditions, the

background becomes corrupted and object/blob

detection becomes erroneous.

To address the above issues, in the following

section a two-fold approach is proposed to tackle

this. In the first step, we carry out segmentation on

the FEM meshes prior to the rasterisation stage. This

prevents regions becoming even fuzzier and

facilitates the estimation of accurate measurement

results, which is a prerequisite for the extraction of

much needed ventilation parameters. In the second

step, we use a probabilistic model, which

accommodates both temporal and spatial contiguity

of mesh element values in order to segment and

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

216

extract regions of conductivity changes directly from

the EIT lung FEM meshes.

3 METHOD

3.1 Dealing with Non-rectangular

Grids

The basis of the proposed approach is segmentation

of conductivity changes on the actual FEM meshes,

rather than the post-processed, rasterised images.

This necessitates assigning a label to each triangular

or tetrahedral element on the FEM mesh in order to

access their coordinate positions. Unlike traditional

images, which are typically based on rectangular

grids, meshes can be of any shape and their

constitutive elements maybe triangles in 2D or

tetrahedra/ hexahedra in 3D. This restricts the

applicability of image processing approaches, which

are commonly implemented on rectangular grids. In

the proposed method, we use the centroid of each

triangular element composing the mesh (in our case,

a 2D cross section of the thorax) as the

representative of that particular element and we

repeat this for all elements in the mesh. The

coordinates of the centroids form the inputs for

subsequent processing. A visual interpretation of the

centroid concept on a sample mesh of the thorax

obtained from EIDORS (Adler, 2006) is shown in

Figure 2.

The next stage of the method consists of three

steps. Firstly, we use anatomical information

regarding the position of the lungs in the thorax to

extract elements belonging to the background and

obtain a prior model of the background by fitting a

Gaussian to the trajectory of each background

element value,

Bkg

E , as it varies in time. Secondly,

the change of mesh element values through time is

modelled as an ‘element process’ and a Gaussian

probability distribution is fitted to this

trajectory,

ele

E . Thirdly, an additional model,

corresponding to the change of the sum of each

element’s neighbourhood associations through time,

is formed by fitting a Gaussian probability model.

The term ‘neighbourhood association’, denotes the

connectivity neighbourhood value

.conn

E of mesh

element

),(

rE , where ),(

r are the polar

coordinates of the elements’ centroid, which consists

of the number of adjacent triangles in the mesh that

share a common edge with the current element. An

example of neighbourhood association of the 251

element is shown in red patches in the mesh of

Figure 2.

Figure 2: Centric assigned to each mesh element.

For this particular element the connectivity

parameter will be

()

∑

−=

),(),(

iiconn

rErEE

θθ

(2)

This parameter will be calculated for all elements

in each frame in the sequence and a Gaussian model

will be fitted to its trajectory. Finally, each new

mesh element is classified by the closeness of its fit

to the three Gaussian distributions (i.e.,

Bkg

ele

and

.conn

E ).

3.2 Statistical Background Model

As previously discussed, the first task involves

modeling of the background. This is achieved by

using anatomical structure of the lung lobes. As

observed in Figure 1(a), several layers exist between

the lung lobes and the surface of the skin, i.e., skin

tissue, fat layers, muscles covering the thorax and

the thoracic skeleton, which protects the lungs.

(a)

(b)

Figure 3: (a) Image progression is from left to right, top to

bottom. Full-breath cycle is shown. (b) Variance mesh

(Brighter regions correspond to higher conductivity

variance).

AUTOMATIC SEGMENTATION OF CONDUCTIVITY CHANGES IN ELECTRICAL IMPEDANCE TOMOGRAPHY

IMAGES

217

This suggests that elements close to the boundary

of the thorax do not form part of the lung lobes and

thus background samples maybe extracted from

these regions. In order to validate this hypothesis,

we consider a sequence of reconstructed EIT FEM

images corresponding to one of the patients in our

dataset. The cycle is shown in Figure 3(a).

Next, we calculate the variance of each element

over this period, and produce a variance image, as

shown in Figure 3(b). As it is clearly seen, the lung

lobes display the highest conductivity changes,

followed by the adjacent darker region (depicted in

red and black colours), which separates them from

the other layers; we were able to reproduce such

variance ‘pattern’ images for all patients in the

dataset. Hence, the two most distant element layers

from the mesh centre were used as background

samples. For all of these elements in a frame

sequence, we model their change trajectory as a

random variable that follows a Gaussian

distribution

),(~

,,, jijiji

σμ

)(

)),(

(

πσ

−−

(3)

where

is a pixel-wise random variable which

follows a Gaussian distribution, located at the

position in the

i EIT frame sequence. ),(

are

the corresponding mean and standard deviation

parameters of the Gaussian distribution. Hence,

background mesh element values over time are

modelled as a time series, which is called an element

process.

Methods employing time-adaptive per-pixel

mixture of Gaussians (MoG) are a popular choice

for modelling scene backgrounds at the pixel level

(Stauffer, 1999). In our application, one Gaussian

sufficed, and moreover such methods are not

appropriate for EIT, since we are not interested to

merely segment out the foreground, but rather the

lung lobes. This is better understood by examining

Figure 3(b). It can be clearly seen that the current

background model is not sufficient for lung lobe

conductivity change segmentation. Specifically, the

central region mesh elements also exhibit constant

changes of conductivity; however, they do not

belong to the lung lobes. For example, if we

threshold the elements of this mesh using the 75

percent Quantile of the variance values we get the

FEM shown in Figure 4.

As it can be seen in this figure, central regions

also show a large degree of change in conductivity,

Figure 4: Thresholded variance image.

hence a Gaussian model fitted to the mesh element

trajectories could indeed belong to the foreground;

however, it may not necessarily form part of the

lobes, which is the objective of this work. In order to

resolve this problem, we build two further element

process models, namely

ele

E and

.conn

E , the first

representing changes of an individual element in

time (excluding previous elements used for the

background model) and the second representing the

region attribute process in time, as discussed before.

So, if the new element centroid was not classified as

part of the initial background model, it would be part

of the foreground but it may or not correspond to the

lobe regions that we are after. Next, by comparing

its value to our other two probabilities calculated

for

ele

E and

.conn

E we can then calculate whether it

maximizes both these probabilities ensuring which

only an element in the lobe region might do.

3.3 Element Classification

Each background element has its own threshold

value, which can be obtained from the

corresponding standard deviation. In this respect, the

proposed method is similar to the adaptive method

described in (Stauffer, 1999), i.e., a per-element/per-

distribution thresholding method. The details of the

algorithm are as follows:

1) Calculate Background model

),(

bgbg

σμ

2) For each element in current frame calculate

}2,1{),,( =−=Η etrE

ieiie

μθ

ieie

bgbg

4) if

bgie

T<Η

then element is background,

update background. Go to Step 6 else it’s a

possible lobe

5) if

bgie

ieie

element belongs

to the lung lobe region. Go to Step 2.

6) ),,()1( trE

iieie

−

),,()1( trE

iieie

−

Here,

),,( trE

is an element in a current frame

(

i in the sequence),

is the mean of the

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

218

element-wise Gaussian distribution,

is the mean

for the regional attribute distribution,

are

the corresponding element-wise standard deviations,

respectively,

Η is the absolute difference between

E and the distribution means,

and

T are the

element-wise thresholds for

Bkg

E ,

ele

E and

.conn

E ,

is the learning rate of the background and

the threshold gain.

),(

bgbg

σμ

is pre-calculated

and is not updated to accommodate for faster

computation speed.

4 EXPERIMENTS AND RESULTS

4.1 Data Acquisition and Processing

Data were collected from a group of 10 male

subjects with no known respiratory or cardiac

abnormalities (age: mean 32; age range, 27-42). In

each case, the 16 element adjacent electrodes were

placed around the subject’s lower thorax (4

-6

intercostal space on the mid-clavicular line). The

subjects lay supine, and were asked to relax and

breathe normally during a 3 min recording. A total

of 2340 frames were recorded using a Sheffield

mark 1 EIT system, using a 50 kHz current drive

(Brown B. H. and Seagar A. D., 1987).

The measured voltage data were then imported

into EIDORS and the inverse problem was solved

using the Gauss-Newton reconstruction algorithm on

a 2D, 576-element thorax mesh model, shown in

Figure 2. The FEM triangulation results were not

parameterized on a 2D pixel grid after the

reconstruction, in order to prevent further resolution

deterioration.

4.2 Gaussian Fitting and Element

Classification

Next, the normalized element value trajectory

alongside the regional attribute trajectory was fitted

by two separate Gaussian models. More specifically,

the recent history of each element,

)},,(,),1,,({ trErE

eleele

…

alongside the sum of

its regional attributes

)},,(,),1,,({ trErE

connconn

…

were modelled by the two Gaussian distributions.

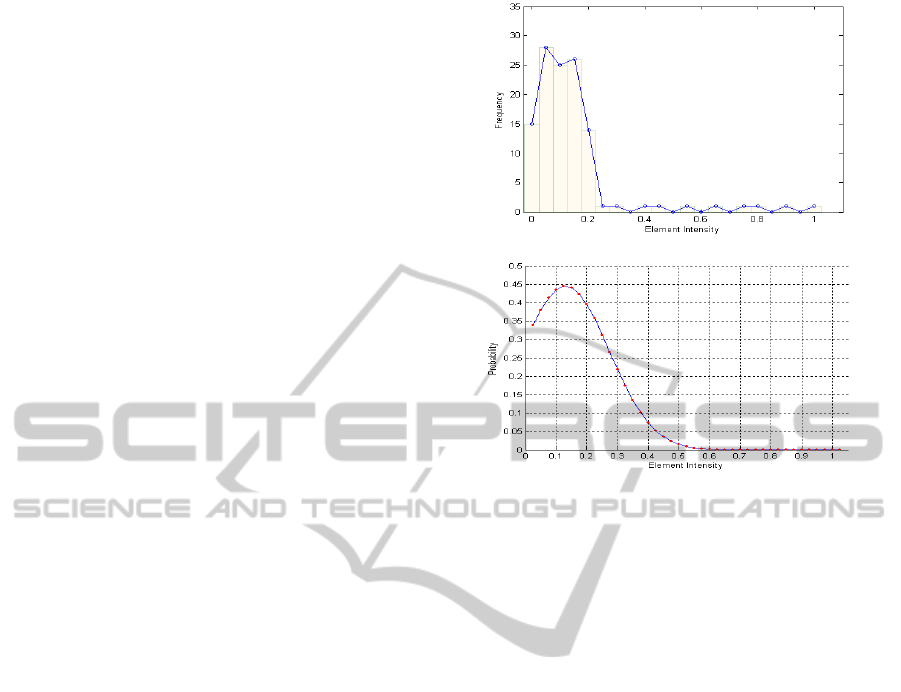
The process of fitting the 251

element of the mesh

of figure 2, which is located in the upper left region

of the mesh, is shown in Figure 5 for

ele

E .

Finally, for each new frame, each of its elements

(a)

(b)

Figure 5: (a) Intensity histogram for the 251

element in

time (b) Fitted Gaussian probability distribution.

is classified to background or lung lobe region

according to the algorithm described in section III.

For the experiments, the learning rate parameter

was set to 0.002, while

= 2.5 gave the best

classifications. The results of the proposed method

on the EIT sequence of Figure 3(a) are shown in

Figure 6.

The effectiveness of the proposed method can be

seen from Figure 6. It shows that the probability

models were able to separate out the non-lung lobe

regions and picked out only areas of high

conductivity changes produced by the lobes without

producing outliers. With the proposed approach, the

use of regional information of each element as it

evolves through time permits the detection of the

globality of the change, recovering the correct

changes in the lobes.

5 CONCLUSIONS

The work proposes a novel, probabilistic method for

extracting regions of conductivity changes in EIT

lung images. The method involves modelling each

mesh element and its regional attribute as a time

series process fitted by a Gaussian model. Moreover,

a prior model of the background was also obtained

using anatomical structure of the thorax. The results

obtained from the different patient data show that

AUTOMATIC SEGMENTATION OF CONDUCTIVITY CHANGES IN ELECTRICAL IMPEDANCE TOMOGRAPHY

IMAGES

219

(a)

(b)

Figure 6: Segmentation results; image progression is from

left to right, top to bottom. Full-breath cycle is shown. (a)

proposed method (b) time-adaptive per-pixel MOG

method described in (Stauffer, 1999).

this new approach can be successfully applied to

automatically segment regions of conductivity

changes in EIT lung images. The procedure requires

minimal input fine-tuning and can capture the

dynamics of distinctly different regions in EIT

images. Further work involves the use of parallel

processing to speed up the segmenta-ion process so

that it can be used in real-time, for longer time

periods, and the extension of the framework to

segmentation on 3D meshes.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge financial

support of this research through the grant provided

by the Engineering and Physical Sciences Research

Council (EPSRC) under Grant EP/E029868/1.

REFERENCES

Ackermann M.J., 1995. The Visible Human Project.

http://www.nlm.nih.gov, 1995. The authors gratefully

acknowledge financial support of this research through

the grant provided by the Engineering and Physical

Sciences Research Council (EPSRC) under Grant

EP/E029868/1.

Adler A. and Lionheart W. R. B., 2006. Uses and abuses

of EIDORS: An extensible software base for EIT.

Physiol Meas, 27:S25 {S42}

Brown B. H. and Seagar A. D., 1987. The Sheffield data

collection system, Clin. Phys. Physiol. Meas., 8,

(Suppl A) 91{97}.

Brown, B.H., 2003. Electrical impedance tomography

(EIT): a review, J Med Eng Technol. vol.:27, pp.97-

108.

Clay M.T. and Ferree T.C., 2002. Weighted regularization

in electrical impedance tomography with applications

to acute cerebral stroke. IEEE Trans. Med. Imaging,

Vol. 21, pp.629–37.

Frerichs I., 2000. Electrical impedance tomography (EIT)

in applications related to lung and ventilation: a review

of experimental and clinical activities. Physiological

Measurement, Vol. 21, no. 2, p. R1.

Frerichs, I., Scholz, J., and Weiler, N., 2006. Electrical

Impedance Tomography and its Perspectives in

Intensive Care Medicine. In J.L. Vincent (Ed.),

Yearbook of Intensive Care and Emergency Medicine,

Berlin: Springer, vol.10, pp. 437-444,

Molinari, M., 2003. High Fidelity Imaging in Electrical

Impedance Tomography. Ph.D. thesis, University of

Southampton, Southampton, United Kingdom.

Smallwood R. H., Hampshire A.R., Brown B.H., R. A.,

Primhak, Marven S. S., and Nopp P., 1999. A

comparison of neonatal and adult lung impedances

derived from EIT images. Physiological Measurement,

Vol. 20, pp. 401-413.

Stauffer M. C., and W. Grimson, 1999. Adaptive

background mixture models for real-time tracking.

IEEE Computer Society Conference on Computer

Vision and Pattern Recognition (Cat. No PR00149).

IEEE Comput. Soc. Part Vol. 2.

Sylvester J. and G. Uhlmann, G., 1986. A uniqueness

theory for an inverse boundary value problem in

electrical prospection. Commun. Pure Appl. Math.,

Vol.39, pp.91–112.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

220