UNIFIED MODELING OF SEVERAL PERTURBATION

EXPERIMENTS IN SYSTEMS BIOLOGY

A Case Study on the Glucose Uptake of Lactococcus Lactis

Andr´as Hartmann

1,∗

, Susana Vinga

1,2

and Jo˜ao M. Lemos

1,3

INESC-ID, R. Alves Redol 9, 1000-029 Lisboa, Portugal

FCM-UNL, C. M´artires P´atria 130, 1169-056 Lisboa, Portugal

IST-UTL, Av. Rovisco Pais, 1049-001 Lisboa, Portugal

Keywords:

Systems biology, Lactococcus lactis, Modeling, Glucose uptake.

Abstract:

Dynamic modeling of the metabolism is one of the main research areas of systems biology. A typical but

yet unresolved problem is the modeling of glucose uptake of Lactococcus lactis bacteria upon in-vivo NMR

measurements in perturbation experiments. Most modelers are focusing on the inverse problem, namely to

identify the parameters of a set of differential equations using the available dataset. Majority of the available

models suffer from the drawback that even if a perfect ﬁt to a single experiment was achieved, they can not

explain the systems’ behavior in different experimental conditions.

The aim of this study is to introduce an appropriate method and a model to ﬁt one set of parameters to several

different experiments, enabling unify modeling of the glucose decay of the bacteria.

With the proposed approach a good overall ﬁt was obtained to the dataset. The results conﬁrm that this could

be a future way towards uniﬁed modeling of data with heterogeneous experimental conditions.

1 INTRODUCTION

The aim of inverse modeling is to capture the systems’

dynamic in a set of parameterized Ordinary Differen-

tial Equation (ODE). However, in systems biology the

modeling task is still not certain. Problems can arise

from the available dataset: the distribution of the mea-

surement points might be uneven, and the values are

often manually transcribed. The measurements are in

many cases corrupted with unknown noise, and only

a subset of metabolites are measurable. Other prob-

lems are caused by the the model itself: to capture

the dynamic, nonlinear models are needed, but the

identiﬁcation of this type of models is far from triv-

ial (Ashyraliyev et al., 2009). Too many parameters

in the model may lead to overparametrisation (Vinga

et al., 2008), sloppyness (Daniels et al., 2008; Vilela

et al., 2009) and / or identiﬁability problems (Srinath

and Gunawan, 2010), not to mention the need of enor-

mous computationalcapacity because of the exponen-

tially growing parameter space. Finally, many mod-

els are ﬁtted to a single experiment only. Neverthe-

less, the so identiﬁed models might explain the given

dataset, but in many cases lack in predictive power

to other experiments. An another consequence of the

above is that even if a very close ﬁt has been achieved

to a single experiment, deterministic models might be

ﬁtted to the unknown noise as well.

The signiﬁcance of good modeling of the glucose

uptake of Lactococcus lactis bacteria is crucial, be-

cause all the other metabolite concentrations of in-

terest depend on this process, see eg. in (Neves

et al., 2005). Recently, (Castro et al., 2009) revealed

the pathways of glucose uptake, however to our best

knowledge, no unique model ﬁt to different experi-

ments of the glucose uptake has been published before

in the literature. This might be due to the fact that the

sigmoidal shape observed in perturbation experiments

is typically difﬁcult to represent with a simple power-

law function (Goel et al., 2008). Modelers often dis-

regard a good ﬁt to external glucose, as (Goel et al.,

2008), or treat the glucose as input function, eg. (Voit

et al., 2006), even the models that accomplish a good

ﬁt, provide different parameters for different experi-

ments, eg. (Vinga et al., 2008).

Here we introduce an approach based on Particle

Swarm Optimization (PSO) , and a model to glucose

uptake of Lactococcus lactis in perturbation experi-

ments. Our approach has proven useful to ﬁt one set

of model parameters to several different experimental

309

Hartmann A., Vinga S. and M. Lemos J..

UNIFIED MODELING OF SEVERAL PERTURBATION EXPERIMENTS IN SYSTEMS BIOLOGY - A Case Study on the Glucose Uptake of Lactococcus

Lactis.

DOI: 10.5220/0003158103090312

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2011), pages 309-312

ISBN: 978-989-8425-36-2

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

conditions.

This paper is organized as follows: In section 2

we introduce our method of identiﬁcation, in section 3

the results are described, and further discussed in sec-

tion 4, ﬁnally in section 5 conclusion is drawn and we

point to future work directions.

2 METHODS

In this section ﬁrst we describe the used dataset, then

the method of identiﬁcation is introduced, ﬁnally we

detail the model of the glucose uptake.

2.1 The Dataset

In vivo Nuclear Magnetic Resonance (NMR) mea-

surements open new horizons for systems biology, al-

lowing measurement of metabolite concentrations in

the living cell (Neves et al., 2005). Unfortunately,

in the case of Lactococcus lactis only the extracel-

lular glucose concentration is measured, and the glu-

cose transport should be modeled. Three perturbation

datasets were used, where a bolus of

C labeled glu-

cose was introduced of 20, 40 and 80 mM respectively

to starving bacteria in anaerobe conditions. We also

observed, that the multiple bolus experiments do not

differ much from the single bolus regarding the shape

of the glucose decay.

2.2 Identiﬁcation Method

Particle Swarm Optimization (PSO) (Kennedy and

Eberhart, 1995) is a population based stochastic op-

timization method inspired by the collective intelli-

gence of simple interacting individuals. The tradi-

tional example for such systems is a bird ﬂock seek-

ing for food. The birds do not know the location of the

food, but their distance from it. Sharing this knowl-

edge with the other members of the ﬂock allows them

to follow the bird that is closest to the food.

In practice, PSO is initialized with a set of possi-

ble solutions, called particles (S

) and associated ran-

dom velocities (v

). In every iteration (k) the speed

and location of each particle in the parameter space is

updated as

(k) = wv

(k− 1) + c

(pbest

− S

(k− 1))

+ c

(gbest − S

(k− 1)) (1)

(k) = S

(k− 1) + v

(k), (2)

where w is the inertia describing the impact of the pre-

vious velocity to the current one. The positive con-

stants c

and c

correspond to the acceleration rate

towards the local and global optima respectively. r

and r

are uniform distributed random variables en-

suring the stochastic behavior of the method, pbest

the best solution discovered so far by the i

particle

and gbest is the best solution found in the iteration.

The particle velocities are lower and upper bounded

as v

min

< v

max

. The method can be summarized

in the following steps:

1. Initialize a set of particles

2. Evaluate the objective function to all the particles

3. Update gbest and pbest

for all particles

4. Count the the new velocities using eq(1)

5. Update the particles’ position using eq (2)

6. Repeat from step 2. until the desired precision or

the limit of iterations is reached.

The objective function here is evaluated in terms of

Mean Squared Errors (MSE) of the ﬁt. This method

was already successfully put into practice for infer-

ring metabolic networks (Naval et al., 2006). Our ap-

proach here is different in the sense that we do not aim

to identify all the metabolites, but only focus on glu-

cose, and instead of ﬁtting to one experiment we use

data of three different experiments (see section 2.1).

2.2.1 Fitting to Multiple Experiments

The trivial way to ensure a ﬁt to multiple datasets is

to use a (weighted) objective function, where the ob-

jective to all the datasets are contributing, for example

by taking the sum of them. The drawback of this ap-

proach is that the summarized error surfaces might be

very complex, and the particles might show very slow

convergence or stuck in a local optima. Thus here we

propose an extension to the method by introducing a

random variables to the objective function as follows

G = q

+ q

+ ... + q

, (3)

where G is the objective function, G

...G

are the

MSE values according to the datasets 1...n, and

...q

are random values with the following proper-

ties:

∑

i=1

= 1 and E(q

) =

2.3 The Model

The idea behind our model is to suppose a variable

(θ), and the glucose concentration (x) depends from it

in a power law manner as shown in eqs (4) and (5).

˙x = −kθ

x (4)

θ =

, (5)

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

310

where k and β are parameters, and c is a constant.

Solving eq (5) results the following simple time de-

pendence: θ = α +

, introducing a new parameter:

α. To make the model more ﬂexible, we also intro-

duce the constant fraction to the x variable. The ﬁnal

model is shown in eq (6).

˙x = −k



α+



(6)

3 RESULTS

First we tested if our model is able to capture the dif-

ferent sigmoidal dynamics derived from the different

glucose uptake time-series. To do this, we applied the

model with the constant c = 1 to the single experi-

ments separately. The model was ﬁtted in 100 inde-

pendent runs of the standard PSO algorithm to each

experiment. The identiﬁed parameters and the simu-

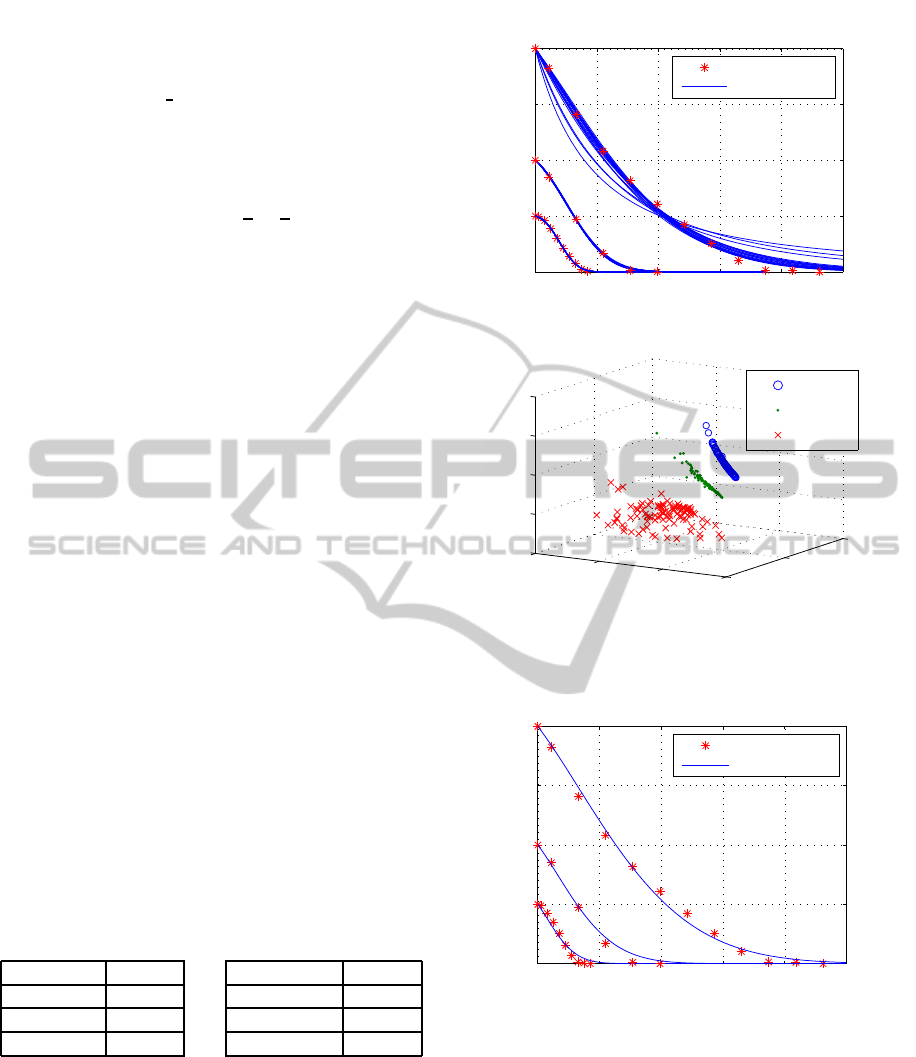
lated time-series are shown in ﬁgure 1. As it can be

seen, this approach allows a good identiﬁcation, how-

ever for the different experimentsthe best revealedpa-

rameters are distinct sets.

For the uniﬁed modeling of the different exper-

iments we have chosen c proportional to the initial

glucose pulse as c

= 1, c

= 2, c

= 4 for the 20,

40 and 80 mMol experiment respectively. Here the

extended version of PSO was used for identiﬁcation

to change the weights dynamically as described in the

previous section. As seen on ﬁgure 2 we managed

to achieve an overall good ﬁt to all the three experi-

ments. Using 50 particles, the method discovered the

parameters seen in table 1, here the Mean Squared Er-

rors (MSE) to the experimental data are also shown in

table.

Table 1: The parameters obtained for our model on the three

experiments using the extended version of PSO (left) and

the MSE values to the experiment (right).

Parameter Value

k 0.2631

α 1.0557

β 0.8347

Experiment MSE

20 mM 2.0718

40 mM 2.2654

80 mM 2.9335

4 DISCUSSION

In connection to many models of systems biology it

can be argued that the parameters may not be unique

even within the same experiments. This phenomena

can be interpreted either from the side of the biologi-

cal system as sloppyness, or from the modelers point

of view a poorly constrained model resulting in bad

0 5 10 15 20 25

Time (min)

Concentration (Mm)

measurements

estimated

−1

20 mM

40 mM

80 mM

Figure 1: The ﬁt to the time-series (top) stars are the mea-

sured values, solid lines denotes for the estimates via the

100 identiﬁed parameter sets on each experiment (bottom).

0 5 10 15 20 25

Time (min)

Concentration (Mm)

measurements

estimated

Figure 2: The original data points and the estimations with

the best ﬁtting the model.

identiﬁability. As (Daniels et al., 2008) points out,

different conditions may attract different sets of pa-

rameters of the same biological model. The param-

eters of interest should be chosen from the intersec-

tions of these sets, since using those ensures the good

description of the system within the different condi-

tions. Unfortunately, in the case of using the same

constant c = 1 in the model for different glucose bo-

lus, the explored parameter sets to the single exper-

UNIFIED MODELING OF SEVERAL PERTURBATION EXPERIMENTS IN SYSTEMS BIOLOGY - A Case Study on

the Glucose Uptake of Lactococcus Lactis

311

iments do not overlap, see ﬁgure 1. In our interpre-

tation this indicates the inadequacy of this approach.

However the model ﬁts remarkably to individual ex-

periments, we would like to point out that this only

proves the models ﬂexibility to capture the different

sigmoidal shapes.

By introducing a constant to the model, propor-

tional to the initial glucose bolus we managed to

achieve a good overall ﬁt of the model with the same

set of parameters on different experiments (ﬁgure 2).

The trade-off is that MSE values to particular exper-

iments are moderately high. We found that our ap-

proach was adequate in ﬁtting several experiments.

The random variables in the objective function re-

sulted that the algorithm is dynamically changing the

weights between the experiments, and ensures a good

convergence even if the sum of the error surfaces

would get difﬁcult.

The sigmoid shape of the glucose uptake was found

slightly varying on the different experiments. This

might be a consequence of the different activity of

the glucose uptake systems revealed by (Castro et al.,

2009), or the differences between the transport of the

glucose monomers. We are also aware of that the glu-

cose uptake might be inﬂuenced by other factors, for

example the biomass, a feedback mechanism from the

inside of the cell or the energy level of the cell accord-

ing to (Papagianni et al., 2007). The model could be

extended to involve these aspects.

5 CONCLUSIONS AND FUTURE

WORK

Here we introduced a model to Lactococcus lactis

glucose uptake, and an approach based on PSO to ﬁt it

to three glucose perturbation experiments with differ-

ent glucose input. With our approach a good overall

ﬁt was achieved to the data using one set of parame-

ters. We think that this could be a future way towards

uniﬁed modeling of data with different experimental

conditions.

We can not exclude that our model is not complete,

and additional terms might be missing from it. Our

future work will aim to identify these terms. We

are also considering the distinct modeling of the glu-

cose monomers and to extend the identiﬁcation of the

model to aerobic conditions.

ACKNOWLEDGEMENTS

This work was supported by project DynaMo

(PTDC/EEA-ACR/69530/2006) FCT, Portugal.

REFERENCES

Ashyraliyev, M., Fomekong-Nanfack, Y., Kaandorp, J. a.,

and Blom, J. G. (2009). Systems biology: parameter

estimation for biochemical models. The FEBS jour-

nal, 276(4):886–902.

Castro, R., Neves, A. R., Fonseca, L. L., Pool, W. a., Kok,

J., Kuipers, O. P., and Santos, H. (2009). Charac-

terization of the individual glucose uptake systems

of Lactococcus lactis: mannose-PTS, cellobiose-PTS

and the novel GlcU permease. Molecular microbiol-

ogy, 71(3):795–806.

Daniels, B. C., Chen, Y.-J., Sethna, J. P., Gutenkunst, R. N.,

and Myers, C. R. (2008). Sloppiness, robustness, and

evolvability in systems biology. Current opinion in

biotechnology, 19(4):389–95.

Goel, G., Chou, I.-C., and Voit, E. (2008). System estima-

tion from metabolic time-series data. Bioinformatics,

24(21):2505.

Kennedy, J. and Eberhart, R. (1995). Particle swarm opti-

mization. of IEEE international conference on neural,

4:1942–1948.

Naval, P., Sison, L., and Mendoza, E. (2006). Metabolic

network parameter inference using particle swarm op-

timization. In International Conference on Molecular

Systems Biology, pages 3–4.

Neves, A. R., Pool, W. a., Kok, J., Kuipers, O. P., and San-

tos, H. (2005). Overview on sugar metabolism and its

control in Lactococcus lactis - the input from in vivo

NMR. FEMS microbiology reviews, 29(3):531–54.

Papagianni, M., Avramidis, N., and Filiousis, G. (2007).

Glycolysis and the regulation of glucose transport in

Lactococcus lactis spp. lactis in batch and fed-batch

culture. Microbial cell factories, 6:16.

Srinath, S. and Gunawan, R. (2010). Parameter identiﬁabil-

ity of power-law biochemical system models. Journal

of biotechnology.

Vilela, M., Vinga, S., Maia, M. a. G. M., Voit, E. O., and

Almeida, J. S. (2009). Identiﬁcation of neutral bio-

chemical network models from time series data. BMC

systems biology, 3:47.

Vinga, S., Thomaseth, K., Lemos, J., Neves, A., Santos,

H., and Freitas, A. (2008). Structural analysis of

metabolic networks: a case study on lactococcus lac-

tis. In 8th Portuguese Conference on Automatic Con-

trol (CONTROLO2008), pages 566–571.

Voit, E., Neves, A., and Santos, H. (2006). The intricate

side of systems biology. Proceedings of the National

Academy of Sciences, 103(25):9452.

BIOINFORMATICS 2011 - International Conference on Bioinformatics Models, Methods and Algorithms

312