
INFERENCE OF BRAIN MENTAL STATES FROM
SPATIO-TEMPORAL ANALYSIS OF EEG SINGLE TRIALS
Yehudit Hasson-Meir, Andrey Zhdanov
The Balvatnik School of Computer Science, Tel-Aviv University, Tel-Aviv, Israel
Talma Hendler
1
, Nathan Intrator
2
1
The Functional Brain Imaging Unit, Wohl Institute for Advanced Imaging, Tel Aviv Sourasky Medical Center, Israel
2
The Balvatnik School of Computer Science, Tel-Aviv University, Tel-Aviv, Israel
Keywords: EEG, Brain computer interface, Regularization, Spatio-temporal analysis.
Abstract: We present an efficient and robust computational model for brain state interpretation from EEG single trials.
This includes identification of the most relevant time points and electrodes that may be active and contribute
to differentiation between the mental states investigated during the experiment. The model includes a
regularized logistic regression classifier trained with cross-validation to find the optimal model and its
regularization parameter. The proposed framework is generic and can be applied to different classification
tasks. In this study we applied it to a classical visual task of distinction between faces and houses. The
results show that the obtained single trial prediction is significantly better than chance. Moreover, correct
choice of the regularization parameter significantly improves classification results. In addition, the obtained
spatial-temporal information of brain activity can give an indication to correlated activity of regions of the
brain (spatial) as well as temporal activity correlations between and within EEG electrodes. This spatial-
temporal analysis can render a far more holistic interpretability for visual perception mechanism without
any a priori bias on certain time periods or scalp locations.
1 INTRODUCTION
A major challenge in neuroscience is inferring how
momentary mental states are mapped into a
particular pattern of brain activity. Inference, which
is based on EEG single-trial (i.e. short segment of
the EEG) has practical implementations for brain
computer interface (BCI) applications. Those BCI
applications are designated for people suffering from
physical disabilities, by helping them to
communicate with an electronic device through
decoding their brain signals in real time (Wolpaw
et al., 2002; Allison et al., 2007; Dornhege et al.,
2007; Blankertz et al., 2007).
The most common way to analyze EEG single-
trials is through classification (for review, see Lotte
et al., 2007). One of the main challenges of
classifying EEG single-trial signals is the amount of
data needed to properly describe the different states.
The later increases exponentially with the
dimensionality of the data; this is known as the curse
of dimensionality problem (Bellman, 1961).
To reduce the dimension of the data, many feature
selection methods have been developed for
identifying and choosing an optimal subset of
features from the data. Often, researchers focus on
few electrodes based on algorithms for channel
selection, which pick the most promising channels
for classification. Muller et al. (2000) utilized
Spatial Pattern Analysis and PCA for channel
selection and compared it to a set of four electrodes
chosen based on prior knowledge.
As a result,
Spatial pattern analysis enhanced the higher
classification rate; (Palaniappan et al., 2002) and
(Schröder et al., 2003) found the appropriate
channels via a Genetic Algorithm; (Lal et al., 2004)
used Recursive Feature Elimination and Zero-Norm
Optimization to reduce the number of electrodes
from 39 to 12. (Tomika and Muller, 2010) reduced
the dimension of the data by down-sampling the
signals.
59
Hasson-Meir Y., Zhdanov A., Hendler T. and Intrator N..
INFERENCE OF BRAIN MENTAL STATES FROM SPATIO-TEMPORAL ANALYSIS OF EEG SINGLE TRIALS.
DOI: 10.5220/0003159800590066
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 59-66
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Another way to alleviate the curse of
dimensionality is via regularization methods, which
stabilize the solutions by introducing prior
knowledge or by restricting the solution (Jain et al.,
2000; Duda et al., 2001). Cross-validation can be
used to find the optimized model and its
regularization parameter (Tomioka and Muller,
2010; Christoforou et al., 2008; Tomioka et al.,
2007; Zhdanov et al., 2007).
As data is becoming more readily available, it is
more desirable to let the data guide the choice of the
model (namely, determine the most relevant
electrodes and most relevant time points) while
minimizing a-priori assumptions. Therefore, a two-
dimensional representation of the spatio-temporal
predictive information of the brain activity is highly
needed for research and diagnosis, especially for
development of new paradigms, for which the neural
correlates may not be known in advance (Murray et
al., 2008).
Modern data-driven analyses, such as microstate
segmentation (Lehmann and Skrandies
, 1980;
Lehmann et al., 1987), have been developed and
used to study the spatio-temporal activity in the
brain. Microstate segmentation uses the spatial
distribution of the ERP which involves averaging
over multiple trials of similar brain activity (for
review, see Murray et al., 2008). Such a predictive
map lacks the correlated activity between electrodes.
This correlation information is lost in the traditional
ERP approach. Moreover, the ability to assess the
trial-to-trial variability in event-related potential
experiments can provide new insights into brain
function which may be ignored during ERP
averaging.
(Tomioka and Muller, 2010) suggested an EEG
single trials spatio-temporal interpretation, which
was based on three different regularizers. The
regularizers were used to reveal different and
complementary aspects of the localization of the
discriminative information. (The channel selection
regularizer was used for spatially localizing the
discriminative information, the temporal-basis
selection regularizer localized the discriminative
information in the temporal domain and the DS
regularizer provided a small number of pairs of
spatial and temporal filters that showed both spatial
and temporal localization of the discriminative
information in a compact manner). The regularizers
were applied on a block diagonal data matrix
concatenated first order changes (short segment of
filtered EEG signal with C channels and T sampled
time-points) and second order changes (the
covariance matrix of a short segment of band-pass
filtered EEG). The proposed model has shown
competitive performance against conventional
methods.
However, the deriving complexity of the learning
problem is high due to the size of the data matrix.
Moreover, using down sampling for reducing the
data dimension does not solve the problem, as it
ignores important properties of the signal, which are
visible in the EEG high temporal resolution. The use
of different regularizers (Tomioka and Muller, 2010)
may be problematic as it may produce contrasting
interpretations with no clear ability to determine
which of them is more accurate.
In this work, we follow the framework introduced
by (Zhdanov et al., 2007) and present an efficient
and robust computational model for brain state
interpretation from EEG single trials. Our approach
is based on the use of regularization techniques to
optimize the classifier coefficients and find the
correct model. We further demonstrate how to
identify the most relevant time points and electrodes
that might be most pertinent in contributing to
differentiation between the mental states
investigated.
Our approach employs a two-step classification:
First we locate the most informative time points and
the most active electrodes in these time points. Then
we try to combine some time points together to
analyze the information flow in the brain related to
the paradigm. This two-step framework allows us to
use a small number of parameters (dozens of
parameters compared with thousands parameters in
(Tomioka and Muller, 2010)) and maintain a high
temporal resolution of the EEG data. In addition, our
spatio-temporal analysis of the brain activity is
presented in one model, which makes it clear and
easy to interpret.
The proposed framework is generic and can be
applied to different classification tasks. In this study
we applied it to a classical visual task of distinction
between faces and houses.
2 MATERIALS AND METHODS
2.1 Experiment Setup
Four subjects (SUBJ1-SUBJ4, 4 females, two left
handed, aged 23-28), participated in this experiment.
All subjects gave informed consent to participate in
the study, which was approved by the ethics
committee of the Tel Aviv Sourasky Medical
Center. Subjects were presented with images from
two different categories-faces and houses. The
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
60

images of faces were taken from the (Ekman and
Friesen, 1976) and (Lundqvist et al., 1998) databases
and include fearful or neutral facial expression.
The experiment included 4 sessions, each of 138
epochs 2- seconds-long. During each epoch, the
subject was presented with one image of a fearful
face, neutral face, house or blank (32, 32, 64 and 10
epochs respectively). To achieve visual field
segregation, participants were explicitly instructed to
ignore the pictures and to concentrate on a fixation
dot at the center of the screen. Throughout the
experiment, participants were asked to report the
color change of the central fixation dot.
2.2 EEG Data Acquisition
Continuous EEG data was recorded simultaneously
with fMRI acquisition. In this study, we are focusing
on the EEG data and have set aside the combined
fMRI data for further research. Good signal-to-noise
ratio of the EEG data in the combined approach was
previously shown at our lab (Sadeh et al., 2008;
Ben-Simon et al., 2008).
We used a 32-channel BrainCap electrode cap
with
sintered Ag/AgCl ring electrodes (30 EEG
channels, 1 ECG channel and 1 EOG cannel, Falk
Minow Services, Herrsching-Breitbrunn, Germany)
and a MR-compatible, 32-channel, battery-operated
amplifier (Brain Products, GmBH, Germany). The
electrodes were positioned according to the 10/20
system. The reference electrode was between Fz and
Cz (
Laufs et at., 2003). The signal was amplified,
and sampled at 5000 Hz using the Brain Vision
Recorder software (Brain Products). The EEG data
was transmitted from the scanner room via an
optical fiber to a PC in the control room. The exact
timing of stimulus onset and MRI scanner gradient
switching was transmitted to the EEG amplifier and
recorded together with the EEG signal.
2.3 EEG Analysis
EEG analysis were performed with EEGLAB 6.01
software package (Schwartz Center for
Computational Neuroscience, University of
California, San Diego), MATLAB software and
FMRIB plug-in for EEGLAB, provided by the
University of Oxford Centre for Functional MRI of
the Brain (FMRIB). Pre-processing of the EEG data
included the following steps: MR gradient artifacts
removal and Cardio-ballistic artifacts removal using
a FASTR algorithm implemented in FMRIB plug-in
for EEGLAB (Sadeh et al., 2008; Ben-Simon et al.,
2008).
For computational efficiency, the EEG signals
were down-sampled to 250 Hz and eye blinking
artifacts were removed using ICA (Delorme et al.,
2001). The data was then filtered with a 0.5–45 Hz
band-pass filter and segmented into epochs starting
100 ms before the stimulus onset and ending 600
after the stimulus onset. Baseline correction was
performed using the 100ms of pre-stimulus activity.
In this manner for each subject, we obtained
several dozens of epochs, each containing 32
(number of channels) x 175 (number of time
sampling points in the segmented interval) values.
Each epoch was associated with a class label "face"
or "house" according to the stimulus which was
presented.
3 BRAIN STATE MODELLING
In this section, we introduce the proposed brain state
modelling approach for EEG single trials spatio-
temporal analysis. Figure 1 shows the flowchart of
the ensemble method.
Figure 1: Brain state modelling flow chart.
The essence of the modelling approach is creating a
parametric family of classifiers and seeking an
optimal member of this family by model selection
techniques. The parameter which forms the
collection of classifiers controls the bias/variance
tradeoff (i.e. regularization parameter), thus a
classifier with optimal bias/variance is chosen
INFERENCE OF BRAIN MENTAL STATES FROM SPATIO-TEMPORAL ANALYSIS OF EEG SINGLE TRIALS
61
(Geman and Bienenstock, 1992). Each member of
the family attempts to predict the mental states of the
brain by finding the coefficients of the model which
mostly differentiate the EEG data into two mental
states. The selection of the optimal member is done
based on the classifier ability to predict the mental
states of the brain.
3.1 Model Estimation
Cross-validation is used for choosing the best model
and estimating its predictive accuracy. This method
is computationally expensive but is especially
important when the number of samples is small.
Cross-validation is applied twice: first for dividing
the original data into train and test sets. We search
for the optimal model on the train sets and check its
accuracy on the test sets. For this we used m-k-fold
cross validation, where k is the number of unique
test sets, and m is the number of times, this process
is repeated. Second, an additional inner n-fold
cross-validation procedure is applied for selecting
the optimal model on the training sets, where n is the
number of averaged cross-validation iterations.
In the first cross validation procedure, the original
data is partitioned into k disjoint sets. A single
dataset is retained as the test data for testing the
model, and the remaining k − 1 disjoint datasets are
used as training data. The cross-validation process is
then repeated k times, with each of the k sets used
exactly once as the test data. We repeat this process
m times. The training sets are used for choosing the
best model and the test sets are used to check its
predictive accuracy. The predictive accuracy of the
model is defined as the number of wrongly predicted
samples divided by the overall number of samples.
The second cross-validation operation is used for
choosing the optimal model. The training dataset is
randomly splitted, n times, into 80-20% training and
validation sets respectively. The classifier runs on
the training set with different values of the
regularization parameter (within the range of
interest) and selects the one that yields the best
results (i.e. bring mean square error, MSE, to
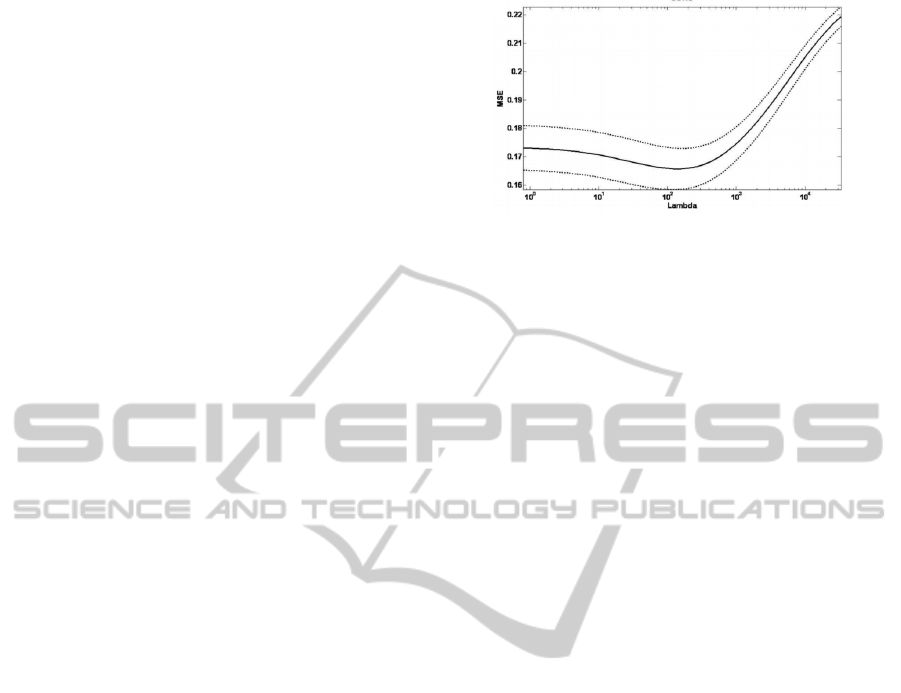
minimum) (see Figure 2).
The range of regularization values of interest is
determined using the singular values, which are
obtained from SVD decomposition of the processed
data matrix (used for training and testing). The range
is bounded between the minimal and the maximal
singular values. For computational efficiency, the
actual regularization values in that range are
distributed uniformly on the logarithmic scale (i.e.
the ratio of the two successive samples is constant).
Figure 2: MSE received on the validation set at the best
time point versus the log of the regularization parameter.
The lambda that minimizes the average error across
iterations is chosen to be the optimal regularization
parameter for the model.
3.2 Regularized Logistic Regression
The proposed regularized brain state interpretation
can be used with a variety of linear and nonlinear
classifiers. The, logistic regression model is the
appropriate one for a binary classification task. It is
also optimal in terms of simplicity, interpretability
of its coefficients and speed (Hosmer and
Lemeshow
, 1989; Friedman et al., 2001).
A useful variable is the odds ratio, which is
defined as the ratio of the probability that an event
occurs to the probability that it fails. The logit (log
odds) of the logistic regression model is given by the
following equations, where
i
w are the model's
coefficients:
pp
xwxwxwwxg ++
+
+
=
...)(
22110
(1)
)1/()()|1(
)()( xgxg
eexxYP +===
π
(2)
)()))(1/()(log(log xgxxodds =−
=
π
π
(3)
The coefficients are often estimated via the
Maximum Likelihood Estimation (MLE) method,
which seeks to maximize the log likelihood over the
entire observed data:
)|(log)(
1
∑
=
==
n
i
ii
xyYPwl
(4)
The log likelihood value represents how likely the
dependent variable can be predicted from the
observed values of the independent variables.
Maximization of the above expression can be done
in various ways, most popular being the Newton-
Raphson (NR) algorithm.
The regularized version of the logistic regression
algorithm seeks to find the weights (w) which
maximizes the equation:
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
62

wwwlwl
T
2
)()(
λ
λ
−=
(5)
We use the Matlab-based MVPA toolbox (Detre
et al., 2006), which implements regularized logistic
regression following notes from (Minka, 2003).
3.3 Features Selection
As mentioned before, one of the main challenges
while working with EEG signals is the high data
dimensionality. In this case, feature selection is
important for reducing the dimensionality of the
input signal, removing noise, improving learning
performance, speeding up the learning process and
improving predictive accuracy.
Feature selection is defined as the process of
choosing an optimal subset of features according to
a certain criterion. The problem of feature selection
has been extensively researched by the machine
learning/pattern recognition community over the
years (Lotte et al., 2007).
In this study, we implement a two step feature
selection algorithm. First we employ the selection of
32 electrodes from a single time point as an input for
the classifier in the same manner as in (Zhdanov et
al., 2007), second, we combine informative time-
points together as an input for the classifier.
We obtain a set of T trials labeled data samples,
each represented by NxM signal matrix, where N is
the number of channels and M is the number of time
sampling points in the segmented interval. For each
time point (from M), we create a feature vector that
contains the EEG data of the entire electrodes in this
time point. (This reduces the dimension of the data
from 32
175 to 32). Afterwards, a family of
classifiers is constructed with different
regularization parameters and applied on the
different time points. The model which achieved the
minimum MSE on the validation set, over the entire
time points, is chosen.
After selecting the model, we evaluate the
predictive accuracy of each time point using the test
sets, by applying the best model on each time point
and averaging the results. The outcome of this stage
is a ranking of the entire time points according to the
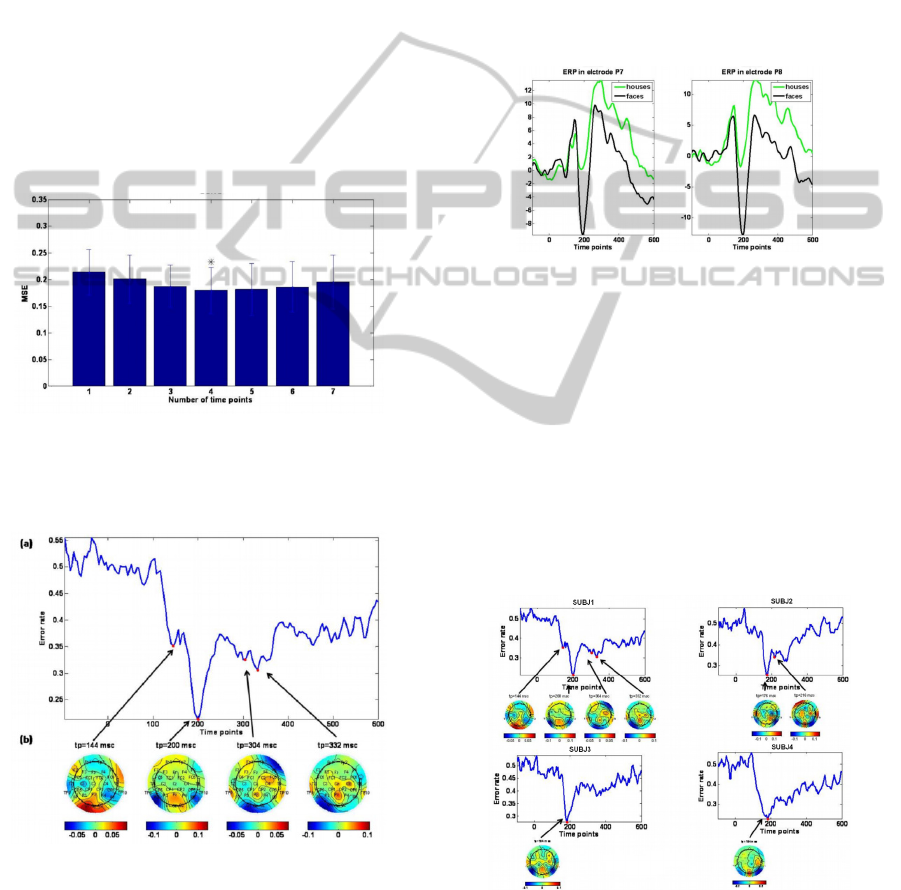
performance of the model (Figure 3). The best time
point with the lowest error rate, best separates
between the brain mental states. The coefficients of
the regression equation at the time point where
minimal prediction error is achieved indicate the
contribution of activity in different electrodes in this
time point towards the prediction. This can be
interpreted as the strength of activity in electrodes
Figure 3: (a) Predictive accuracy of each time point, on the
testing set. The black line show the average error rate over
the cross-validation iterations and the blue line represents
control results obtained using the same algorithm on data
with randomly scrambled target labels. It can be seen that
the best prediction is achieved around 200ms after the
stimulus onset (N170). (b) The coefficients of the
regression equation in the best time point. The coefficients
indicate the most contributing electrodes in this time point;
Blue color indicates strong negative effect of faces
compared to houses.
which best contributes to the mental states
separation.
The formulation presented so far indicates the
most predictive time point and the configuration of
electrodes at that time point. This spatial coding,
where the prediction depends on a configuration of
electrodes activity as a single time point, may not be
the optimal code used by the brain in interpreting the
stimuli. Therefore it is possible that a temporal or
spatio/temporal coding is more appropriate.
The presented model can address this question,
although the computational problem involved
becomes too big for a single computer to handle, but
thanks to a computer grid of several hundred
personal computers, the model can be extended in
this direction.
In this aspect we sort the local minima in the
prediction graph to find different distinct temporal
locations with prediction error minimum. The
sorting was done in an increasing order (starting
from the most predictable time point to the least
predictable time point). Then a collection of models
is applied, each using an increasing amount of
information, where new time points (electrode
information) are added into the model. In each such
input data configuration we perform the full cross-
validation estimation to estimate optimal
regularization and prediction error.
Time points were sequentially added to the model
using a wrapper algorithm (Kohavi and John, 1997),
which is a feature selection technique for selecting
an optimal subset of features from a large search
INFERENCE OF BRAIN MENTAL STATES FROM SPATIO-TEMPORAL ANALYSIS OF EEG SINGLE TRIALS
63
space. The features were assessed according to their
usefulness to a given predictor and added to the
subset, one by one. The ten most predictable time
points were included in this process and they were
added to the model according to their contribution to
the overall prediction.
We compared the outcome of the classifier for a
different number of time points and choose the ideal
number of time points which has significantly lower
error prediction (Figure 4). Increasing the input
vector adds electrode activity data, but also adds free
parameters to the model leading to higher chance of
overfitting the training data. We thus search for the
ideal number of time points which balances between
the two effects. Figure 5 shows the best time points
found for one subject and the electrodes activity in
these time points contributing towards mental state
discrimination.
Figure 4: prediction error vs. number of time points. For
this subject the optimal is 4, namely there was a
significant prediction improvement up to that point
(**p<0.05).
Figure 5: (a) The ideal number of time points chosen as
input for the classifier. (b) The regression coefficients
received in those time points.
4 RESULTS
4.1 Spatio-Temporal Analysis
Many studies have shown that pictures of faces elicit
a much larger ERP of negative polarity than other
object categories. This component peaks at occipital-
temporal electrode sites at about 170 ms following
stimulus onset (Bentin et al., 1996). The larger
response of the N170 complex to faces is an
undisputed observation among researchers in the
field of face processing. (Figure 6).
Figure 6: ERP in electrodes P7 and P8.
We reinforce this result using EEG single trial
classification (Figure 7). For all subjects the best
prediction achieved around 200 ms after the stimulus
onset and the electrodes that contribute to the
maximum separation between the mental states
investigated are located in the occipital area. The
coefficients obtained on single trial training
correlated to the ERP of the corresponding
electrodes. Negative coefficients indicate the ERP
for faces is lower than the ERP for houses. In
addition, both occipital electrodes (P7 and P8) are
correlated in that time point.
Figure 7: Best time points found and the coefficients in
these time points for different subjects in the houses and
faces experiment. As expected, for the entire subjects the
best prediction is achieved around 200ms after the
stimulus onset and the most activated electrodes are in the
occipital-temporal area.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
64
The resulting spatial-temporal weight matrix
provides a summary representation which is easily
interpretable. A result of the dimensionality
reduction, which is performed during the pre-
processing stage, where relevant time points and
electrodes are chosen, leads to simpler
computational model training. This is in contrast to
reducing the dimensionality via reducing the
sampling rate (Tomioka and Muller, 2010).
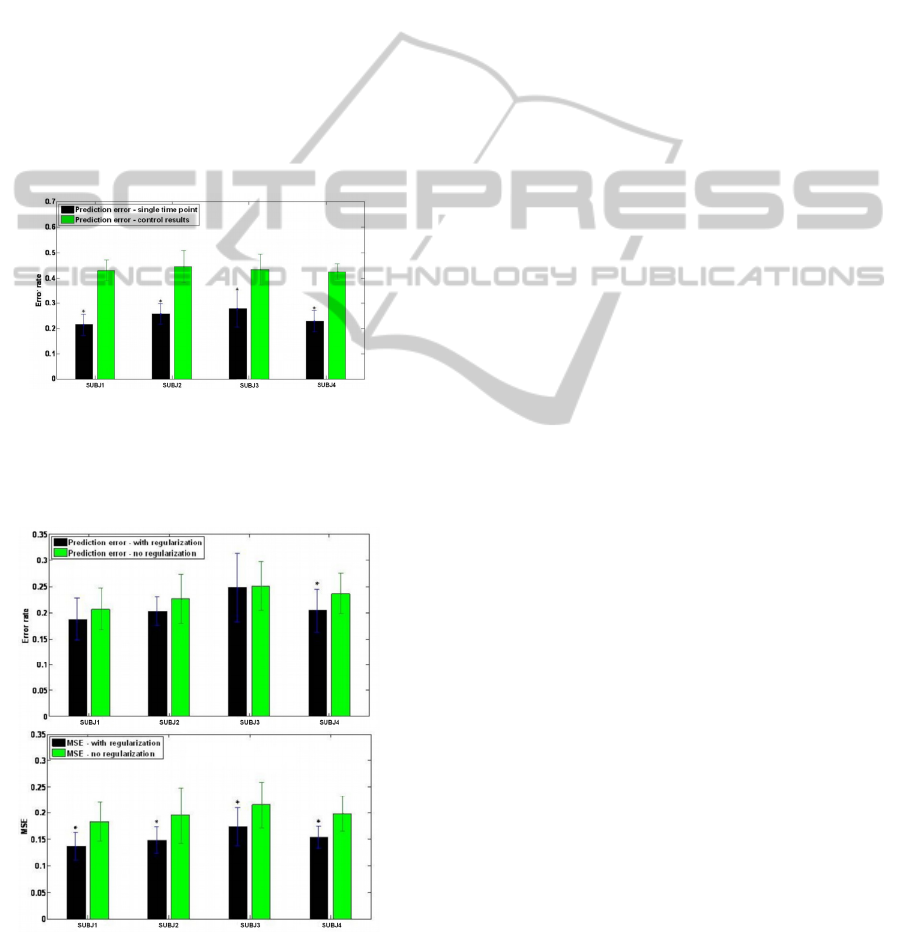
The lowest error rates achieved for each subject
using a single time point are summarized in Figure 8
(the prediction error with the optimal number of
time points is lower). The results were compared to
the control experimental results, which were
obtained using the same algorithm on randomly
scrambled labels. The difference between the mean
error estimates is significant for all subjects (P <
0.05).
Figure 8: Classification error rate for all 4 subjects. The
classification error is compared to control results obtained
using the same algorithm on randomly scrambled labels.
The difference between the mean error estimates is
significant for all subjects (*p<0.05).
Figure 9: Prediction error (Error rate and MSE) received
for 3 best time points chosen, with and without
regularization. These figures show that results with
regularization are significantly better (*p<0.05).
4.2 The Impact of Regularization
The amount of data needed to properly describe the
different mental states increases exponentially with
the dimensionality of the feature vectors. As the
amount of training data is small compared to the size
of the feature vectors, the classifier is likely to
overfit to the training data and thus producing a
model which does not uncover the true brain state
discrimination. The only way to avoid this and still
get a reliable brain state interpretation is a robust
training with a regularizer which has to be carefully
picked. To demonstrate the effect of non optimal
regularization selection, we applied the same
algorithm, with and without a regularization
parameter on feature vector of size 96 (three best
time points). As it can be seen in Figure 9, the
classification error with regularization is
significantly lower (P < 0.05).
5 CONCLUSIONS
We have proposed a robust and efficient framework
for brain state interpretation using EEG single trials.
This framework is based on extensive feature
selection using a regularized logistic regression
classifier and can be used for spatial-temporal
analysis of the EEG data. This spatial-temporal
analysis, which indicates best electrodes and best
time points, can render a far more holistic
interpretability without any a priori information on
certain optimal time points or electrode locations. It
can thus indicate whether the coding related to the
brain state discrimination task is spatial, temporal or
joint, and can indicate the network of information
propagation (at high temporal resolution) following
the stimuli. This method, which can also be applied
to a Time/Frequency representation of the signal,
can also reveal the different frequency bands at
which brain state discrimination is optimal.
ACKNOWLEDGEMENTS
This research was supported by Israeli Scientific
Foundation converging technologies program.
REFERENCES
Allison, B. Z., Wolpaw, E. W., Wolpaw, J. R., 2007. Brain
computer interface systems: progress and prospects.
Expert review of medical devices, 4 (4), pp.463-
474(12).
INFERENCE OF BRAIN MENTAL STATES FROM SPATIO-TEMPORAL ANALYSIS OF EEG SINGLE TRIALS
65

Bellman, R. E, 1961. Adaptive Control Processes.
Princeton University Press, Princeton, NJ.
Ben-Simon, E., Podlipsky, I., Arieli, A., Zhdanov, A.,
Hendler, T., 2008. Never resting brain: Simultaneous
representation of two alpha related processes in
humans. Plos One, 3 (12), e3984.
Bentin, S., Allison, T., Puce, A., Perez, E., McCarthy, G.,
1996. Electrophysiological studies of faces perception
in humans. Journal of Cognitive Neuroscience, 8(6),
pp. 551-565.
Blankertz, B., Dornhege, G., Krauledat, M., Müller, K. R.,
Curio, G., 2007. The noninvasive Berlin brain-
computer interface: fast acquisition of effective
performance in untrained subjects. NeuroImage, 37(2),
pp. 539–550.
Christoforou, C., Sajda, P., Parra, L. C., 2008. Second
order bilinear discriminant analysis for single trial
EEG analysis. Advances in Neural Information
Processing Systems, 20, pp. 313–320.
Delorme, A., Makeig, S., Sejnowski, T., 2001. Automatic
artifact rejection for EEG data using high-order
statistics and independent component analysis.
Proceedings of the 3rd International ICA Conference.
Detre, G., Polyn, S. M., Moore, C., Natu, V., Singer, B.,
Cohen, J., Haxby, J. V., Norman, K. A., 2006. The
Multi-Voxel Pattern Analysis (MVPA) Toolbox.
Poster presented at the Annual Meeting of the
Organization for Human Brain Mapping, Italy.
Dornhege, G., Millán, J. del R., Hinterberger, T.,
McFarland, D., Müller, K.-R. (Eds.), 2007. Towards
Brain-Computer Interfacing. MIT Press.
Duda, R. O., Hart, P. E., Stork, D. G., 2001. Pattern
Recognition 2nd edn (New York: Wiley-Interscience)
Ekman, P., Friesen, W., 1976. Pictures of facial affect,
Consulting Psychologists Press, Palo Alto, CA.
Friedman, J., Hastie, T., Tibshirani, R., 2001. The
elements of statistical learning. Springer.
Geman, S., Bienenstock , E., 1992. Neural networks and
the bias/variance dilemma. Neural Computation, 4 (1),
pp. 1–58.
Hosmer , D. W., Lemeshow, S., 1989. Applied logistic
regression. New York: John Wiley, pp. 118-24.
Jain, A. K., Duin, R.P.W.,Mao, J., 2000. Statistical pattern
recognition: a review IEEE Trans. Pattern Anal.
Mach. Intell. 22, pp.4–37
Kaper, M., Meinicke, P., Grossekathoefer, U., Lingner, T.,
Ritter, H., 2004. BCI competition 2003–data set llb:
support vector machines for the p300 speller paradigm
IEEE Trans. Biomed. Eng. 51, pp.1073–6.
Kohavi, R., John, G., 1997. Wrappers for feature subset
selection. Artificial Intelligence, 97 (1-2), pp. 273-324.
Lal, T., Schröder, M., Hinterberger, T., Weston, J.,
Bogdan, M., Birbaumer, N., Schölkopf, B., 2004.
Support vector channel selection in BCI. IEEE Trans.
Biomed. Eng., 51(6), pp. 1003–1010.
Laufs, H., Krakow. K., Sterzer. P., Eger. E., Beyerle. A.,
Salek-Haddadi. A., Kleinschmidt. A., 2003.
Electroencephalographic signatures of attentional and
cogntive default modes in spontaneous brain activity
fluctuations at rest. Proceedings of the National
Academy of Sciences, U.S.A., 100, 11053–11058.
Lehmann, D., Skrandies, W., 1980. Reference-free
identification of components of checkerboard-evoked
multichannel potential fields. Electroencephalogr Clin
Neurophysiol, 48 (6), pp. 609–621.
Lehmann, D., Ozaki, H. and Pal, I. 1987. EEG alpha map
series: brain microstates by space-oriented adaptive
segmentation. Electroenceph. clin. Neurophysiol., 67
(3), pp. 271-288.
Lotte, F., Congedo, M., Lécuyer, A., Lamarche, F.,
Arnaldi, B., 2007. A review of classifcation algorithms
for eeg-based brain-computer interfaces. Journal of
Neural Engineering, 4 (2), pp. R1.R13.
Lundqvist, D., Flykt, A., Ohman, A.,1998. The Karolinska
Directed Emotional Faces (KDEF), Department of
Neurosciences, Karolinska Hospital, Stockholm, UK.
Minka, T., 2003. A Comparison of Numerical Optimizers
for Logistic Regression. technical report, Dept. of
Statistics, Carnegie Mellon University.
Muller, T., Ball, T., Kristeva-Feige, R., Mergner, T.,
Timmer, J., 2000. Selecting relevant electrode
positions for classification tasks based on the electro-
encephalogram. Medical and Biological Engineering
and Computing, 38(1), pp. 62–67.
Murray, M. Brunet, M., Brunet, D., Michel, C. 2008.
Topographic ERP analyses: step-by-step tutorial
review. Brain Topography, 20 (4), 249–269.
Palaniappan, R., Raveendran, P., Omatu, S., 2002. VEP
optimal channel selection using genetic algorithm for
neural network classification of alcoholics. IEEE
Transactions on Neural Networks, 13(2), pp. 486–491.
Sadeh, B., Zhdanov, A., Podlipsky, I., Hendler, T., Yovel,
G., 2008. The validity of the face-selective ERP N170
component during simultaneous recording with
functional MRI. Neuroimage, 42 (2), pp.778–786.
Schröder, M., Bogdan, M., Rosenstiel, W., Hinterberger,
T., Birbaumer, N., 2003. Automated EEG Feature
Selection for Brain Computer Interfaces, Proceedings
of 1st International IEEE EMBS Conference on Neural
Engineering, Capri Island, Italy.
Tomioka, R., Aihara, K., Müller, K. R., 2007. Logistic
regression for single trial eeg classification. In:
Schölkopf, B., Platt, J., Hoffman, T. (Eds.), Advances
in Neural Information Processing Systems 19. MIT
Press, Cambridge, MA, pp. 1377–1384.
Tomioka, R., Müller, K. R., 2010. A regularized
discriminative framework for EEG analysis with
application to brain-computer interface. Neuroimage.
49 (1), pp.415-32.
Wolpaw, J. R., Birbaumer, N., McFarland, D. J.,
Pfurtscheller, G., Vaughan, T. M., 2002. Brain–
computer interfaces for communication and control
Clin. Neurophysiol. 113 (6), pp. 767–91.
Zhdanov, A., Hendler, T., Ungerleider, L., Intrator, N.,
2007. Inferring functional brain States using temporal
evolution of regularized classifiers. Comput. Intell.
Neurosci, p. 52609.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
66
