AUTOMATIC DEPTH ELECTRODE LOCALIZATION

IN INTRACRANIAL SPACE

Janis Hofmanis, Valerie Louis-Dorr, Olivier Caspary and Louis Maillard

Research Centre for Automatic Control, Institut National Polytechnique de Lorraine

2, av. de la fort de Haye, Vandoeuvre-les-Nancy, France

Keywords:

Electrode localization, SEEG, Coregistration, Matter segmentation, Epilepsy, CT.

Abstract:

Localization and precise targeting of depth electrodes in the regions of the human brain is critical for accurate

clinical diagnoses and treatment as well as for epileptical source localization and studies of in-vivo electrical

propagation. By using magnetic resonance imaging (MRI) combined with computed tomography (CT), the

authors present a method based on image processing and object recognition that improves electrode local-

ization in different brain anatomies and matter. This method permits the quantiﬁed localization of electrode

placements in cortex and white matter, and gives the precise position of each electrode, allowing a more de-

tailed study of intra-cranial electrical stimulation, propagation and properties of conductivity related to the

brain. Such methods can be extended to depth-scalp signal analysis using simultaneously registered SEEG

and EEG measurements.

1 INTRODUCTION

When investigating the brain processes using stereo

electroencephalography (SEEG) (Talairach et al.,

1974), the main question is how to relate given mea-

surements with spatio-temporal neural source activ-

ity. To do this, it is important to build a model that

incorporates all unknown parameters. Using recent

studies of simultaneously recorded scalp and intrac-

erebral EEG combining with deep brain stimulation

(DBS), it could be possible to relate measurements on

scalp and intracerebral activity. However, to build a

model, one must know the precise position of the elec-

trodes where DBS is executed. It is also important to

understand how the electrical conductivity is affected

by white matter, precisely, ﬁbers of axons. To anal-

yse this in detail, we must know which depth elec-

trodes are located in white and which in gray matter.

There already exist few studies of depth electrode lo-

calization in brain anatomies. Oya (Oya et al., 2009)

presented an atlas based on SEEG electrode localiza-

tion in the amygdala. Ekstrom (Ekstrom et al., 2009)

showed how to use MRI, and 2D computational un-

folding can localize electrodes in the subregions of the

hippocampus and the parahippocampal gyrus. Both

these methods concentrate on anatomy structure seg-

mentation and not so much on electrode placements

in three dimensional brain space. Miller (Miller et al.,

2007) has constructed the Matlab package ”Location

on Cortex” to help localize subdural electrodes using

lateral X-ray images. However, this method enables

to apply subdural electrode arrays onto a standardized

template brain volume and requires neurologists to

pinpoint each electrode position manually. There are

also applications like BioImage Suite (Yale Univer-

sity, USA) (Duncan et al., 2004) that allow to edit and

place manually multicaptors or grid of electrodes ac-

cording to their position in CT scan image. This, how-

ever, is time-consuming when working with many pa-

tients and multicaptors. In this paper, the objective of

electrode localization is to develop an automatic rou-

tine that ﬁnds the origin of each electrode in 3-D CT

scan.

1.1 Acquisition Methods

Usually, the collector of electrodes, called multicap-

tor, consists of 10 or 15 separate electrodes each 2mm

wide and 0.8mm in diameter separated by 1.5mm of

isolator. For one patient, 10 multicaptors can be im-

planted, of total from 100 to 150 electrodes. Before

surgery of multicaptors, MR imaging (3D SPGR T1

weighted-sequence, TR: 20 ms, TE: 6 ms; matrix 512

X 512, with double injection of gadolinium) is applied

459

Hofmanis J., Louis-Dor V., Caspary O. and Maillard L..

AUTOMATIC DEPTH ELECTRODE LOCALIZATION IN INTRACRANIAL SPACE.

DOI: 10.5220/0003160204590462

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 459-462

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

to obtain the conﬁguration of brain anatomy for par-

ticular patients. After implementation, CT with voxel

size variating from 0.5 x 0.5 x 0.7 mm to 0.6 x 0.6 x

0.7 mm is done.

2 SEEG ELECTRODE

LOCALIZATION IN MATTER

Finding the position of intracranial electrodes and

their location with respect to brain matter can be de-

scribed in three steps: 1. Register the electrodes

in CT. 2. Co-register CT and preimplant MRI (ﬁnd

transformation matrix). 3. Do matter segmentation

in MRI volume. The ﬁnal step consists in calculating

the electrodes position by use of the transformation

matrix. If the boundaries are known, then we can de-

termine each electrode in matter spaces (see Figure 1).

The following sections explain these steps in detail.

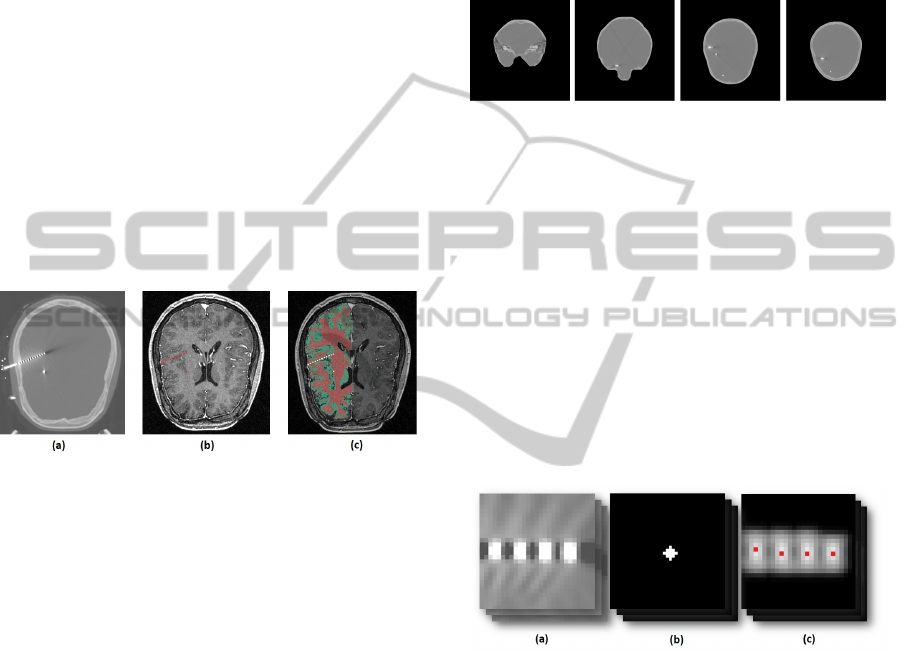
Figure 1: (a) - A slice of a CT image with electrodes, (b) -

slice of MRI with approximate position of electrodes (red),

sition of electrodes (white).

2.1 Electrodes Localization in CT Scan

• skull stripping;

• correlation of the pattern;

• identiﬁcation of the multicaptor;

• optimization of 3D localization.

Each of these steps is explained in detail below.

2.1.1 Skull Stripping

In order to make electrode recognition routines work

optimally, extraneous artifacts that do not contain

depth electrodes, must be removed from the images.

This includes all data outside the skull and intracra-

nial space where multicaptors are located. There are

many studies for fast skull stripping in MRI (Dale

et al., 1999; Hahn and Peitgen, 2000) and CT scan

(Maldjiana et al., 2001; Lee et al., 2008). Suggestions

for skull stripping together with implanted depth elec-

trodes was not found. Furthermore, some electrodes

can be located in the skull itself, so we need a method

for segmenting the area of intracranial space together

with the skull. To satisfy these conditions, we devel-

oped a procedure based on intensity level threshold-

ing and image morphological processing methods to

segment intracranial space. The result of four seg-

mented slices is shown in the Figure 2 below.

Figure 2: CT image slices after skull stripping.

2.1.2 Correlation of the Pattern

In the next step we apply a 3D correlation to seg-

mented (skull stripped) intracranial volume with a

simulated pattern, which is an approximation of one

electrode. The retained pattern is a little sphere whose

size is determined by the size of the voxel (Figure 3

(b)). We use the spherical object because it has ro-

tation invariant properties and it is more robust in a

blurred environment. The correlation of CT scan and

pattern gives local maximums (in voxel space), where

the pattern matches the electrodes (Figure 3 (c) - red

points).

Figure 3: (a) - Blurred electrodes in slice of CT scan, (b) -

approximated pattern of electrode, (c) image of correlation

result (maximums marked as red points).

Unfortunately, as the mask used for the skull strip-

ping retains some parts of the headholder (which is

close to the boundary of the skull), the pattern corre-

lation results in several false maximums that do not

correspond to the electrodes, and for some multicap-

tors, due to angle with CT slice, electrodes were so

blurred that correlation produced several maximums

for one electrode.

2.1.3 Identiﬁcation of the Multicaptor

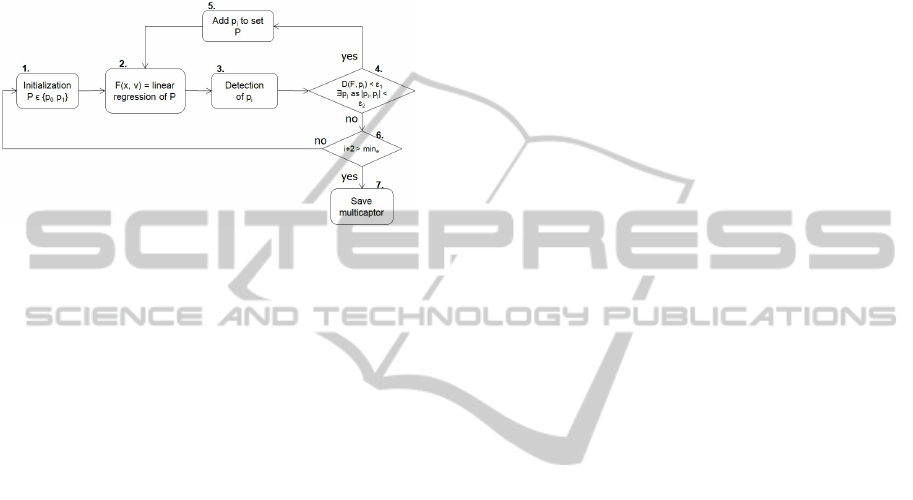
A improved method which correctly interprets the lo-

cal maximums of the 3D correlation function is pro-

posed for separation and recognition of multicaptors

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

460

and recognition of each electrode in these multicap-

tors. First, this method analyses given local maxi-

mum points, detects all sets of points corresponding

to the multicaptor and eliminates all other points. This

method can be summarized in 7 steps that are repeated

until all multicaptors are identiﬁed (see chart in Fig-

ure 4):

Figure 4: Action diagram of registration of multicaptors.

1. Initialize ﬁrst points P = {p

, p

} for multicaptor.

2. Do 3D linear regression as F(x,~v) =

argmin

x,~v

∑

N−1

j=0

[(p

− F(x,~v))

], where x and ~v

is line’s F midpoint and direction vector, re-

spectively, and N is the number of points in set

3. Detect p

= g

, where g

= argmin

[D(F, g

)], g is

the set of all points and D is the distance from

point g

to line F.

4. IF D(F, p

) < ε

AND ∃p

∈P as | p

− p

|< ε

DO step 5 ELSE DO step 6. The operator | · |

denotes the vector norm.

5. Add p

to P and repeat all steps starting form step

6. IF i + 2 (number of electrodes) > min

DO step 7

ELSE go to step 1. Here, min

is minimal elec-

trode amount for one multicaptor (given by neu-

rologists).

7. Save P as multicaptor and remove points of set P

from set g.

For the algorithm, we choose value of ε

as 5.75mm

(this corresponds to one distance and a half between

two electrodes alongside) and ε

as 2mm (adjusted

from a priori knowledge of the mean electrode for 4

patients).

2.1.4 Optimization of 3D Localization

Usually, after the correlation and identiﬁcation

phases, points of multicaptors are not distributed

equally on the line and have some shifts along differ-

ent directions. Therefore, the electrodes of one multi-

captor need to be corrected according to the real elec-

trode position with a priori knowledge of the space

between electrodes. This is carried out by minimizing

the error function for each multicaptor set P found in

the previous subsection:

error

(δ) =

∑

j=1

argmin

| p

− s

− δ |, (1)

where S = {s

,.. .,s

} is the simulated real

multicaptor with M referring to the number of the

equally spaced electrodes in the same direction as the

multicaptor P = {p

, p

,. . . , p

}. The δ is the shift-

ing variable in direction of the multicaptor and | · | is

the vector norm. Thus we calculate the sum of errors

(distance between real and simulated points of elec-

trodes) for which we ﬁnd the global minimum that

corresponds best to the real multicaptor.

2.2 CT and MRI Co-registration

Considering that electrodes are localized correctly

in post-surgery CT scan, to know their location ac-

cording to matter, two images, CT and MRI, co-

registration must be taken. We resort to Statistical

Parametric Mapping 8 toolbox for Matlab (Trust Cen-

tre for Neuroimaging, UK) in order to register post-

implanted CT with pre-implanted MRI. Registration

is achieved by adjusting the relative position and ori-

entation until the mutual information between the im-

ages is maximized (Wells et al., 1996; Collignon

et al., 1995):

T = argmax

I(u(x), v(T (x))), (2)

where, u is the reference (template) and v is the

test volume (image), x - the random variable of co-

ordinates for the voxel, T is a transformation of the

coordinate frame of the reference volume into the test

volume and I is mutual information between two vol-

umes.

2.3 Matter Segmentation in MRI

The ﬁnal step is labeling the electrode position with

respect to brain matter (white or gray). In the studies

of matter segmentation, several recent methods have

been presented. Hidden Markov Chain models (Bricq

et al., 2008) or Expectation Maximization algorithm

(Dugas-Phocion et al., 2004) can be used to segment

3D data. But in the context of this paper we do not

search for the best performance segmentation but for

the most efﬁcient implementation. So, surface-based

AUTOMATIC DEPTH ELECTRODE LOCALIZATION IN INTRACRANIAL SPACE

461

pipeline method (Dale et al., 1999; Hahn and Peitgen,

2000) introduced in FreeSurfer (Martinos Center for

Biomedical Imaging, USA) is applied.

The segmentation stage allows to extract the

topology of gray/white matter with respect to the po-

sition of each electrode.

3 RESULTS

Four patients underwent MR imaging studies prior to

depth electrode placement (the number of multicap-

tors for the ﬁrst patient was 10, for the second - 11,

the third - 9, and the fourth - 8), altogether 456 elec-

trodes. In those 4 cases CT scan was made to track

the electrode positions. In all CT scans, electrodes

were noticeably blurred and artifacts of wires, hold-

ing frames, were visible. Successful skull stripping

was carried out. After applying correlation with pat-

tern to CT, not only true but also many false electrode

points were calculated. Mainly the false maximum

were located in the area of end of the multicaptors

and in the headholders. Nevertheless, all multicap-

tors were found and center of electrodes were located.

Due to the end of the multicaptor artifact, the algo-

rithm provides 14 false electrodes additionally. How-

ever, for each multicaptor, the number of electrodes

is known, and false electrodes can be eliminated au-

tomatically. Once the electrodes had been identiﬁed,

each patient’s MRI and CT co-registration were com-

puted, and then, transformations of the electrode po-

sitions were calculated. Finally, matter segmentation

was applied respectfully of the gray/white matter.

4 CONCLUSIONS

The electrode localization in the matter can be ap-

plied automatically (except in few minor cases at seg-

mentation stage). A electrode recognition in CT scan

image, and a register of MRI together with CT was

done. Lastly we segment the matter and calculate the

electrode’s position in the brain matter. We put for-

ward a new approach for automatic electrode local-

ization in CT and used some already developed tech-

niques which presented the full circle of automatic

depth electrode localization in the brain matter. This

proposed method is preprocessing stage of forward

modeling within the framework of electrophysiologi-

cal propagation in cerebral structures.

REFERENCES

Bricq, S., Collet, C., and Armspach, J. (2008). Unify-

ing framework for multimodal brain MRI segmenta-

tion based on Hidden Markov Chains. Medical Image

Analysis, 12(6):639–652.

Collignon, A., Maes, F., Delaere, D., Vandermeulen, D.,

Suetens, P., and Marchal, G. (1995). Automated

multi-modality image registration based on informa-

tion theory. Information Processing in Medical Imag-

ing, 1(1):263–274.

Dale, A., Fischl, B., and Sereno, M. (1999). Cortical

surface-based analysis. i. segmentation and surface re-

construction. Neuroimage, 9:179–194.

Dugas-Phocion, G., Ballester, M., Malandain, G., Lebrun,

C., and Ayache, N. (2004). Improved EM-based tis-

sue segmentation and partial volume effect quantiﬁ-

cation in multi-sequence brain MRI. Medical Im-

age Computing and Computer-Assisted Intervention,

pages 26–33.

Duncan, J., Papademetris, X., Yang, J., Jackowski, M.,

Zeng, X., and Staib, L. (2004). Geometric strategies

for neuroanatomic analysis from mri. Neuroimage,

23:34–45.

Ekstrom, A., Suthana, N., Behnke, E., Salamon, N.,

Bookheimer, S., and Fried, I. (2009). High-resolution

depth electrode localization and imaging in patients

with pharmacologically intractable epilepsy. Stereo-

tactic and Functional Neurosurgery, 4(108):812–815.

Hahn, H. and Peitgen, H. (2000). The skull stripping prob-

lem in mri solved by a single 3d watershed transform.

Medical image computing and computer-assisted in-

tervention, 1935:134–143.

Lee, T., Fauzi, M., and Komiya, R. (2008). Segmentation

of ct head images. BioMedical Engineering and In-

formatics, 2:233–237.

Maldjiana, J., Chalelaa, J., Kasnera, S., Liebeskinda, D.,

and Detrea, J. (2001). Automated ct segmentation and

analysis for acute middle cerebral artery stroke. Amer-

ican Journal of Neuroradiology, 22:1050–1055.

Miller, K., Makeig, S., Hebbb, A., Raoc, R., Dennijs, M.,

and Ojemannb, J. (2007). Cortical electrode local-

ization from x-rays and simple mapping for electro-

corticographic research: The location on cortex (loc)

package for matlab. Journal of Neuroscience Meth-

ods, 162:303–308.

Oya, H., Kawasaki, H., Dahdaleh, N., Wemmie, J., and

Howard, M. (2009). Stereotactic atlas-based depth

electrode localization in the human amygdala. Stereo-

tactic and Functional Neurosurgery, 4(87):219–228.

Talairach, J., Bancoud, J., Szikla, G., Bonis, A., Geier, S.,

and Vedrenne, C. (1974). New approach to the neu-

rosurgery of epilepsy. stereotaxic methodology and

therapeutic results. 1. introduction and history. Neu-

rochirurgie, 20:1–240.

Wells, W., Viola, P., Atsumi, H., Nakajima, S., and Kiki-

nis, R. (1996). Multi-modal volume registration by

maximisation of mutual information. Medical Image

Analysis, 1(1):35–51.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

462