TOWARDS A STATISTICAL DESCRIPTION OF EXPERIMENTAL

DATA FOR DETECTION-ESTIMATION PROBLEMS IN DNA

TRANSLOCATIONS THROUGH NANOPORES

S. Michelet

, J-P. Barbot

, O. Franc¸ais

, P-Y. Joubert

, P. Larzabal

R. Kawano

, H. Sasaki

, T. Osaki

, S. Takeuchi

and B. Le Piouﬂe

SATIE, ENS Cachan, CNRS, UniverSud, 61 Avenue du Pr´esident Wilson, Cachan, France

KAST and IIS, University of Tokyo, Tokyo, Japan

Keywords:

Signal processing, Stochastic framework, Detection, Estimation, Characterization of DNA translocations.

Abstract:

This paper investigates the properties of DNA translocations signals in a stochastic framework. The considered

signals are relative to the translocation of single strand DNA through natural nanopores, and are obtained

using a planar patch clamp method. The stochastic signal analysis is carried out considering the statistical

distribution of DNA translocation parameters, considered as random variables including the amplitude, the

duration and the apparition of the DNA translocation events as well as the no-translocation signal features.

For each of these variables, a distribution function is proposed and assessed using a Kolmogorov-Smirnov

test, and their features are estimated. The DNA translocation signal stochastic analysis enables to characterize

the detection and/or estimation performances of existing algorithms, such as a breakdown detection algorithm,

in a stochastic framework. Moreover, it opens the way to the design of model based algorithms such as

detection tests using a likelihood ratio or joint detection-estimation algorithms using a maximum likelihood

approach, for an enhanced characterization of DNA translocations.

1 INTRODUCTION

In view of the DNA sequencing, a biochip dedicated

to the DNA translocation through natural nanopores

reconstituted on an artiﬁcial biomimetic membrane

was designed in (Osaki et al., 2009). The biochip

consists in a partition between a ﬂuidic chamber and

a channel, made with a thin ﬁlm of parylen obtained

by chemical vapor deposition, and micromachined

through oxygen plama (see ﬁgure 1).

The biomimetic artiﬁcial membrane is built up on

this partition, by the successive ﬂow of lipids and

buffers into the channel, as described in (Osaki et al.,

2009) and the nanopore is created thanks to the in-

sertion of an α-hemolysin natural membrane protein.

The application of a voltage on both sides of the mem-

brane induces the movements of ions, and therefore

the apparition of a current through the channel. The

DNA strand crossing through the membrane induces

a current blockade, measured thanks to a patch clamp

ampliﬁer. The amplitude and duration of this block-

ade characterizes the DNA composition and length.

The blockade current constitutes the informative sig-

nal which is sampled and digitalized by the experi-

Figure 1: Presentation of the biochip used for DNA translo-

cation detection.

mental setup. In order to avoid aliasing during the

acquisition process, a so called anti-aliasing low pass

ﬁlter is used to process the experimental data.

Getting DNA translocation signals is a delicate ex-

periment, since the obtained signals depend on many

parameters, such as temperature, humidity, sealing of

the artiﬁcial membrane or surface conditions of the

electrodes.

In this study, in order to avoid repetitive exper-

iments required to adjust the acquisition parameters

221

Michelet S., Barbot J., Francais O., Joubert P., Larzabal P., Kawano R., Sasaki H., Osaki T., Takeuchi S. and Le Piouﬂe B..

TOWARDS A STATISTICAL DESCRIPTION OF EXPERIMENTAL DATA FOR DETECTION-ESTIMATION PROBLEMS IN DNA TRANSLOCATIONS

THROUGH NANOPORES.

DOI: 10.5220/0003160702210226

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 221-226

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

left to the users and the dedicated data processing

techniques, artiﬁcial signals are generated. The prop-

erties of these artiﬁcial signals are determined through

the statistical investigations of actual biosignals. In

section 2 the statistical properties of the signal are

estimated, including the no-translocation current, the

amplitude and duration of the DNA translocations

events, and the delay between events. In section

3, corresponding artiﬁcial signals are generated and

used to optimally design an amplitude-duration char-

acterization algorithm based on a breakdown detec-

tion approach, and used to evaluate the amplitude-

duration characterization performances. In section 4,

thanks to the proposed statistical framework, the rele-

vance of model based approachesis pointed out, in or-

der to develop i) a detection test using likelihood ratio,

and ii) a joint detection-estimation algorithm based on

a maximum likelihood method.

2 A STATISTICAL DESCRIPTION

OF THE DNA

TRANSLOCATION SIGNAL

In this study, the investigation is carried out

in a stochastic framework for the current ﬂow-

ing through the nanopore. The considered ex-

perimental data are relative to the transloca-

tions of a 41mer ssDNA TTTTTTTTTCACTGAC-

CTGGGGGAGTATTGCGGAGGAAGGT, the con-

centration of which is 45 µM in a 1.0 M KCl, 10

mM PBS, 1 mM EDTA buffer featuring pH=7.4. The

DNA translocations are conducted thanks to a 80 mV

voltage applied between both sides of the lipid bi-

layer.

The stochastic characterization of DNA signals

consists in the evaluation of the statistical distribution

of the amplitude, denoted AMP, the duration (DUR),

the delay between translocation (DBT), and the no-

translocation signal (NTS), which are deﬁned in ﬁg-

ure 3.

2.1 Properties of the Current through

Nanopore in Absence of

Translocation

Firstly we examine the statistical properties of the

actual current ﬂowing through an open α-hemolysin

channel nanopore without any DNA stand transloca-

tion. An example of the current ﬂowing through the

nanopore is shown in ﬁgure 4.

An histogram of this no-translocation signal is

shown on ﬁgure 5, which seems to exhibit a Gaussian

205.9 205.95 206 206.05

100

Time (sec)

Current amplitude (pA)

Translocation

Attempt

Figure 2: Examples of current blockades relative to DNA

translocation and translocation attempts.

232.556 232.558 232.56 232.562 232.564 232.566

100

Time (sec)

Current amplutide (pA)

AMP

DBT

DUR

NTS

Figure 3: Features of the DNA translocation signal.

0.496 0.498 0.5 0.502 0.504

Time (sec)

Current amplitude (pA)

Figure 4: Real current variations through α-hemolysin

channel without any translocation event.

90 91 92 93 94 95 96 97 98

Current amplitude

Number of elements

Figure 5: Histogram of no-translocation experimental cur-

rent samples (n=1982 samples).

distribution. The mean and standard deviation param-

eters of the distribution, respectively denoted µ and σ,

are estimated using:

µ =

∑

k=1

x[k] (1)

n−1

∑

k=1

(x[k] −µ)

(2)

where x is the signal and n the number of samples.

Considering the available experimental data, the esti-

mation using eq. (1) and eq. (2) leads to µ

NTS

= 93.7

pA and σ

NTS

= 1 pA.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

222

In order to attest the assumed Gaussian distribu-

tion of the no-translocation signal, a Kolmogorov-

Smirnov (KS) test was implemented. The KS test ac-

tually quantiﬁes the distance between the cumulative

distribution function (CDF) of the considered exper-

imental data, denoted F

(x), and the CDF of a refer-

ence distribution denoted F(x) (Kendall and Stuart,

1979). This KS will be prefered to the Chi-2 test

which is sensitive to a lack of data in the experimental

histogram. The KS distance is expressed by:

√

n×sup

|F(x) −F

(x)| (3)

where n is the number of samples of the exper-

imental data. If this distance D

is greater than a

predeﬁned threshold, then the hypothesis according

to which the experimental data distribution is close to

the candidate reference distribution is rejected. The

threshold is adjusted for a false reject rate of 1%.

Here, the KS test validates the normal distribution

of the no-translocation current, as shown on ﬁgure 6,

which exhibits the CDF F

(x) and F(x).

90 91 92 93 94 95 96 97 98

0.2

0.4

0.6

0.8

Amplitude value

Cumulative distribution function

Gaussian model

Data

Figure 6: Cumulative distribution functions F

(x) (Gaus-

sian) F(x) (experimental data).

2.2 Statistical Properties of

Translocations Events

In this section, we characterize the translocation

events through their duration and amplitude distribu-

tion. Indeed, the translocation event provokes a cur-

rent blockade featured by a duration and an amplitude

which give biological information on the ssDNA. The

amplitude vs time duration graph permits to deter-

mine the length of the DNA, and provides information

about its composition, such as the discrimination be-

tween polyU, polyC or polyA, (Akeson et al., 1999).

As usually admitted (Kasianowicz et al., 1996),

only translocations with a current amplitude decreas-

ing more than 80% of the initial value correspond to

complete translocations. Others are translocation at-

tempts which are not considered here.

2.2.1 Amplitude and Duration of the

Translocation Events

Thanks to equations (1) and (2) the amplitude dis-

tribution mean value and standard deviation of the

translocation amplitude AMP can be estimated: µ

AMP

= 89.2 pA and σ

AMP

= 7.33 pA.

In this study, the translocation current amplitude

AMP is assumed to be normally distributed, and a KS

test implemented has validated this assumption.

In (Meller et al., 2000), the distribution of the

translocation duration was approximated using a mix-

ture of a Gaussian law and an exponentially decaying

law. Here, for tractability purposes, a Rayleigh law

(Eq. 4) seems to be more adequate to ﬁt the DUR

actual distribution law, and will therefore be prefered

(Figure 7). The KS test validates this distribution law.

f(DUR) =

DUR

exp



−

DUR



(4)

For the duration distribution the Rayleigh param-

eter r is estimated according to equation (5).

DUR

∑

k∈[1,n]

(DUR[k])

= 924 µsec (5)

0 0.5 1 1.5 2 2.5 3

x 10

−3

0.2

0.4

0.6

0.8

Duration time (s)

Cumulative distribution function

Rayleigh model

Real data

Figure 7: Cumulative distribution functions F

and F rela-

tive to the Rayleigh distribution of DUR.

2.2.2 Statistics of Delay between Translocations

Events

The distribution of the delay between translocations

(DBT) is considered in this section and assumed to be

a decreasing exponential, expressed by :

f(DBT) = αexp(−αDBT) (6)

where:

α =

∑

i=1

DBT(i)

(7)

α = (17.6ms)

−1

2.2.3 Statistical Description of the DNA

Translocation Signal

Finally, the distribution features of the random vari-

ables AMP, DUR, DBT and NTS, estimated from ex-

perimental DNA translocation signals are gathered in

table 1.

TOWARDS A STATISTICAL DESCRIPTION OF EXPERIMENTAL DATA FOR DETECTION-ESTIMATION

PROBLEMS IN DNA TRANSLOCATIONS THROUGH NANOPORES

223

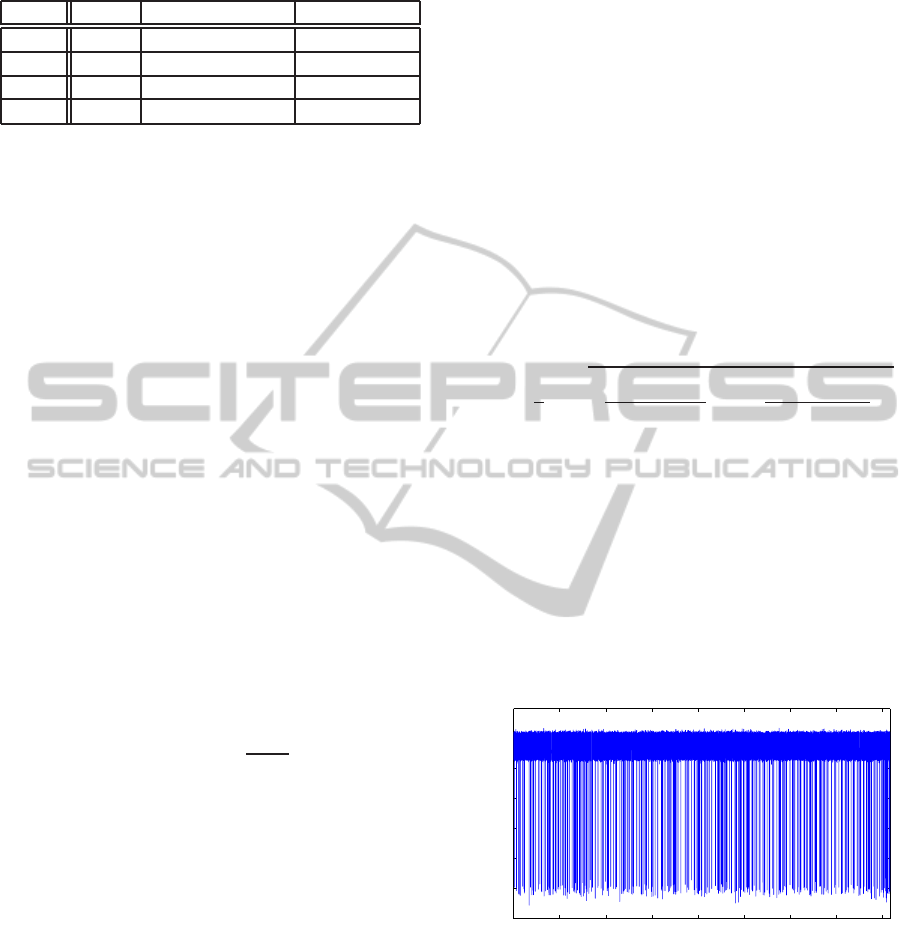
Table 1: Distributions features.

Dist param. 1 param. 2

NTS Gaus. µ = 93.7 pA σ = 1 pA

AMP Gaus. µ = 89.2 pA σ = 7.33 pA

DUR Ray. r = 924 µs

DBT Exp. α = (17.6 ms)

−1

3 PERFORMANCES OF A

NO-PARAMETRIC

AMPLITUDE-DURATION

ESTIMATION ALGORITHM

In this section, the DNA translocation signal charac-

terization results are used to evaluate, in a stochas-

tic framework, the performances of an elementary

translocation characterization algorithm. The con-

sidered algorithm is based on a breakdown detec-

tion technique, presented in (Osaki et al., 2010)

which allows to estimate the amplitude and duration

of translocation events, respectively denoted

[

AMP

and

[

DUR. To evaluate the performances of this char-

acterization algorithm for various signal features, we

build up artiﬁcial biomimetic signal considering the

AMP, DUR, DBT and NTS distributions estimated in

the previous section. Moreover, in order to take the

possible experimental noise variance variations into

account relative to the experimental set-up, we elab-

orate artiﬁcial signals featured by various signal to

noise ratios (SNR), deﬁned as:

SNR = 20log|

AMP

NTS

| (8)

An example of a 319 translocation signal se-

quence featured by a 30 dB SNR is represented in

ﬁgure 8, and ﬁgure 9 exhibits the detail of a sin-

gle artiﬁcial translocation event. The implementation

of the breakdown detection algorithm applied to this

translocation sequence allows the AMP and DUR val-

ues of the 319 translocations to be estimated. The cor-

responding amplitude vs duration representation dia-

gram is depicted in ﬁgure 10.

In order to quantify the characterization perfor-

mances of the algorithm, we compute the true posi-

tive rate and the false positive rate of the character-

ization algorithm, considering SNRs ranging from 6

to 46 dB. The true positive rate (TPR) is computed

as the rate of the estimated AMP-DUR values of each

considered translocation event which are close to the

actual values whithin a prediﬁned distance ν. On

the other hand, the false positive rate (FPR) is de-

ﬁned as the rate of the estimated AMP-DUR values

which are wrongly positionned at a distance smaller

than a varying distance ν. Then, the receiver opera-

tional characteristic (ROC) which plots the TPR as a

function of FPR for various values of ν can be con-

sidered to quantify the characterization performances

(Bradley, 1997). ROC curves obtained for the con-

sidered translocations data are presented in ﬁgure 11.

One can note for example that a 90 % TPR is reached

at the cost of a 0.01 % FPR considering a transloca-

tion sequence with SNR = 28 dB, and that the same 90

% TPR is reached at the cost of a 1 % FPR when the

SNR falls down to 18 dB. An other means of quanti-

fying the performance of the amplitude-duration esti-

mation algorithm is to evaluate the mean square error

(MSE) deﬁned in equation (9), of the characterization

as a function of the SNR of the translocation signal.

MSE =

∑

i=1

[

AMP

−AMP

AMP

[

DUR

−DUR

DUR

(9)

where

[

AMP and

[

DUR are the estimated values

of AMP and DUR respectively, n is the number of

translocations equal to 319, and where the contribu-

tion of the amplitude and duration errors are normal-

ized by their mean values in order to give them the

same weight in the computation of the MSE. The

MSE computed according to equation (9) and ex-

pressed in percent is represented in ﬁgure 12. One can

note that the MSE falls from 30 % to 0.02 % when the

SNR rises from 6 dB up to 46 dB, respectively.

Time (sec)

Current amplitude (pA)

50 60 70 80

-20

100

120

Figure 8: Generated artiﬁcial signal.

4 DISCUSSION

We have proposed a statistical characterization of

nanopore DNA translocation current allowing well

known methods of amplitude/duration characteriza-

tions (Basseville and Nikiforov, 1993) to be imple-

mented and evaluated using intensive computer simu-

lations.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

224

replacements

Time (sec)

Current amplitude (pA)

0.636

0.638

0.64 0.642 0.644 0.646

-20

100

120

Figure 9: Single translocation event in the artiﬁcial signal.

Duration (sec)

Current amplitude decreasing (pA)

0.5

1.5

2.5

3.5 4

×10

−3

100

Figure 10: Diagram duration vs amplitude for the artiﬁcial

translocations.

0 0.005 0.01 0.015 0.02 0.025

0.2

0.4

0.6

0.8

False positive rate

True positive rate

6 dB

12 dB

18 dB

32 dB

28 dB

Figure 11: ROC of the duration-amplitude characterization.

More challenging now is the use of this statis-

tical characterization to optimally build new model

based approaches to improve the characterization per-

formances. The proposed modelling of translocation

signals opens this way. As a complete statistical char-

acterisation of a steplike signal is now available, sev-

eral ways of investigation are opened. Let us brieﬂy

point out two of them for further works:

i) a model based segmentation procedure which

detects multiple change points in a steplike signal can

be built on a generalized likelihood ratio test or on

0 10 20 30 40 50

−2

SNR (dB)

MSE (%)

Figure 12: MSE (eq 9) of the amplitude-duration estima-

tion.

information theoretic criterion such as Akaike infor-

mation criterion like tests. Moreover, since this seg-

mentation technique considers the DNA translocation

signal as a whole sequence, it avoids the well known

drawbacks relative to sliding window data processing

approaches.

ii) a regularized maximum likelihood method can

be built, looking for the unknown parameters θ as:

θ = argmin

{ks∗(t) −s(θ)k

+ λk∇s(θ)k

} (10)

with

θ = [t

, t

...t

, a

...a

]

where t

are the step

location parameters and a

are the step amplitude pa-

rameters.

∇s(θ) is the gradient of the solution. As we are

looking for a steplike signal, for regularization pur-

poses a l

norm will be used for the gradient.

s ∗(t) is the actual recorded signal and s(θ) is a

candidate signal. Recent developments in convexe

constraint optimisation open the way to an efﬁcient

optimisation of the criterium expressed in equation

(10). λ is a parameter used to adjust the contribution

of each terms of the regularization criterion.

This provides a statistical framework for DNA

translocation characterisation.

ACKNOWLEDGEMENTS

This work was supported by grants of a joint CNRS-

JST research program.

REFERENCES

Akeson, M., Branton, D., Kasianowicz, J. J., Brandin,

E., and Deamer, D. W. (1999). Microsecond

time-scale discrimination among polycytidylic acid,

polyadenylic acid, and polyuridylic acid as homopoly-

mers or as segments within single rna molecules. Bio-

physical Journal Volume 77.

Basseville, M. and Nikiforov, I. V. (1993). Detection of

abrupt changes : theory and applications. Prentice-

Hall, Englewood Cliff, NJ.

TOWARDS A STATISTICAL DESCRIPTION OF EXPERIMENTAL DATA FOR DETECTION-ESTIMATION

PROBLEMS IN DNA TRANSLOCATIONS THROUGH NANOPORES

225

Bradley, A. P. (1997). The use of the area under the

roc curve in the evaluation of machine learning algo-

rithms. Pattern Recognition Lett 30(7):1145159.

Kasianowicz, J. J., Brandin, E., Branton, D., and Deamer,

D. W. (1996). Characterization of individual polynu-

cleotide molecules using a membrane channel. Proc.

Natl. Acad. Sci. USA 93.

Kendall, M. G. and Stuart, A. (1979). The Advanced Theory

of Statistics, volume 2. Charles Grifﬁn, 4th edition.

Meller, A., Nivon, L., Brandin, E., Golovchenko, J., and

Branton, D. (February 2000). Rapid nanopore dis-

crimination between single polynucleotide molecules.

PNAS vol. 97.

Osaki, T., Barbot, J., Kawano, R., Sasaki, H., Francais, O.,

Piouﬂe, B. L., and Takeuchi, S. (September 2010).

A rupture detection algorithm for the dna transloca-

tion detection though biological nanopore. accepted

in Proc. Eurosensors XXIV.

Osaki, T., Suzuki, H., Piouﬂe, B. L., and Takeuchi, S.

(2009). Multichannel simultaneous measurements

of single-molecule translocation in α-hemolysin

nanopore array. Analytical Chemistry 81.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

226