FEATURE SELECTION FOR INTER-PATIENT SUPERVISED

HEART BEAT CLASSIFICATION

G. Doquire

, G. de Lannoy

1,2

, D. Franc¸ois

and M. Verleysen

ICTEAM Institute, Machine Learning Group, Universit

e catholique de Louvain

pl. du Levant 3, 1348 Louvain-la-Neuve, Belgium

Institute of Neuroscience, Universit

e catholique de Louvain, av. Hippocrate 54, 1200 Bruxelles, Belgium

Keywords:

Feature selection, Electrocardiogram signal, Heart beat classiﬁcation, AAMI standards.

Abstract:

Supervised and inter-patient classiﬁcation of heart beats is primordial in many applications requiring long-term

monitoring of the cardiac function. Several classiﬁcation models able to cope with the strong class unbalance

and a large variety of ECG feature sets have been proposed for this task. In practice, over 200 features are

often considered and the features retained in the ﬁnal model are either chosen using domain knowledge or an

exhaustive search in the feature sets without evaluating the relevance of each individual feature included in the

classiﬁer. As a consequence, the results obtained by these models can be suboptimal and difﬁcult to interpret.

In this work, feature selection techniques are considered to extract optimal feature subsets for state of the art

ECG classiﬁcation models. The performances are evaluated on real ambulatory recordings and compared to

previously reported feature choices using the same models. Results indicate that a small number of individual

features actually serve the classiﬁcation and that better performances can be achieved by removing useless

features.

1 INTRODUCTION

The diagnosis of cardiac pathologies requires moni-

toring the cardiac function by recording and process-

ing the electrocardiogram (ECG) signal. The diagno-

sis may rely on just a few transient factors of short

duration such as intermittent arrhythmia; long-term

ECG recordings are therefore usually required. The

manual analysis of such long-term ECG signals, con-

taining hundreds to thousands of heart beats to evalu-

ate proves tedious and error-prone.

Several computer-aided heart beat classiﬁcation

algorithms have recently been proposed for this task.

These algorithms can be divided in two categories:

inter-patient or intra-patient classiﬁcation systems

(De Lannoy et al., 2010). Intra-patient classiﬁcation

requires labeled beats from the tested patient in the

training of the model. By contrast, inter-patient mod-

els classify the beats of a new tested patient accord-

ing to a reference database built from data coming

from previously diagnosed patients. In real situations,

labeled beats are usually not timely available for a

new patient which makes the intra-patient classiﬁca-

tion not applicable. For this reason, this work focuses

on inter-patient classiﬁcation.

The ﬁrst study to establish a reliable inter-patient

classiﬁcation methodology is (Chazal et al., 2004),

where a weighted linear discriminant analysis (LDA)

model is trained to classify the beats in the four

classes deﬁned by the standards of the AAMI (As-

sociation for the Advancement of Medical Instru-

mentation, 1998). In (Park et al., 2008), hierarchi-

cal SVMs are considered and in (De Lannoy et al.,

2010), a support vector machine classiﬁer optmizing

a weighted cost function is introduced. These studies

perform feature selection using either domain knowl-

edge (Park et al., 2008) or an exhaustive search at the

group level (De Lannoy et al., 2010; Chazal et al.,

2004) without evaluating the relevance of each indi-

vidual feature included in the classiﬁer. Furthermore,

distinct features groups are considered in each study

which makes it difﬁcult to assess their discriminative

power on a fair basis.

As a consequence, the results obtained by these

models can be suboptimal; indeed it has been shown

in many classiﬁcation tasks that spurious features

can harm the classiﬁer, especially in the presence of

unbalanced classes and a large number of features

(Franc¸ois, 2008; Nguyen et al., 2009). Moreover, fea-

ture selection serves the interpretability of the classi-

Doquire G., de Lannoy G., François D. and Verleysen M..

FEATURE SELECTION FOR INTER-PATIENT SUPERVISED HEART BEAT CLASSIFICATION.

DOI: 10.5220/0003163200670073

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 67-73

ISBN: 978-989-8425-35-5

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

ﬁer, since discriminative features are identiﬁed. This

property is especially useful in medical applications

where the selected features may help to understand

the causes and the origin of the pathologies.

In this work, a large number of features previ-

ously proposed for heart beat classiﬁcation are ex-

tracted and two feature selection methods are inves-

tigated to select optimal feature subsets: the wrapper

and the ﬁlter approaches. Experiments are conducted

on real ambulatory signals from the MIT arrhythmia

database. Section 2 provides a short overview of the

theoretical background on the methods used in this

work. Section 3 details the database used in the exper-

iments and the processing of the ECG signals. Section

4 details the experiments and presents the results.

2 THEORETICAL BACKGROUND

Let us deﬁne the ith p-dimensional observation x

,...,x

} and the associated class value y

for a

given heart beat i with i ranging from 1 to N, N being

the total number of heart beats in the dataset. Tra-

ditional classiﬁers optimizing the accuracy make the

hidden assumption that the classes are equally bal-

anced (Nguyen et al., 2009). However, in a heart

beat classiﬁcation task, around 90% of beats are nor-

mal beats while all the pathological classes represent

the other 10%. For this reason, weights have to be

introduced in the classiﬁer to handle that situation.

Two distinct models are considered in this work: the

weighted LDA model (Chazal et al., 2004) and the

weighted SVM model (De Lannoy et al., 2010).

2.1 Weighted LDA

Let us ﬁrst deﬁne the mean class vectors µ

and the

covariance matrix Σ of the features as

∑

i∈k

(1)

Σ =

∑

k=1

∑

i∈k

− µ

)(x

− µ

)

∑

k=1

(2)

where N

is the number of elements in class k, the

sum over i ∈ k denotes the beats belonging to class k,

and the w

values are the weights introduced in the

covariance matrix to handle the class imbalance.

The weighted LDA is a linear classiﬁer that clas-

siﬁes the beats according to the estimated posterior

probabilities P(y = k|x) using

P(y = k|x) =

exp( f

(x))

∑

k=1

exp( f

(x))

(3)

where K is the total number of classes and

(x) = −(1/2)µ

−1

+ µ

−1

x. (4)

2.2 Weighted SVM

SVMs are linear machines that rely on a preprocess-

ing to represent the features in a high dimension, typ-

ically much higher than the one of the original fea-

ture space. With an appropriate non-linear mapping

ϕ(x) to a sufﬁciently high-dimensional space, ﬁnite

data from two categories can indeed always be sepa-

rated by a hyperplane. In SVMs, this hyperplane is

chosen as the one with the largest margin. The two-

class SVM model for unbalanced data is described in

this section; it can be extended to multi-class tasks

by using the one-against-one or one-against-all ap-

proaches.

Assume each observation x

has been transformed

to z

= ϕ(x

). The soft-margin formulation of the

SVM allows examples to be misclassiﬁed or to lie in-

side the margin by introducing slack variables ξ

the problem constraints:

min.

w,b,ξ

||w||

+C.

N+

∑

{i|y

=1}

N−

∑

{i|y

=−1}

(5)

s.t.



(

w,z

+ b) ≥ 1 − ξ

∀i = 1..N

≥ 0 ∀i = 1..N

(6)

where w and b are the parameters of the hyperplane,

and N

−

denote respectively the number of posi-

tive and negative examples and C is a hyper-parameter

to be tuned. In this SVM formulation, different penal-

ties are introduced for each class in the objective func-

tion so that a convex approximation of the Balanced

Classiﬁcation Rate (BCR) is optimized rather than the

accuray as in the classical SVM formulation. In the

dual form, the explicit form of the mapping function

ϕ must not be known as long as the kernel function

K(x

) = ϕ(x

)ϕ(x

) is deﬁned.

2.3 Mutual Information

The mutual information (MI), introduced by Shannon

in 1948 (Shannon, 1948), has proven to be a very ef-

fective criteria in the context of feature selection as

it is able to detect non-linear relationships between

(groups of) features. The MI of a pair of random vari-

ables X,Y is a symmetric measure of the dependence

between these two variables and is deﬁned as:

MI(X,Y ) = H(X) + H(Y ) − H(X,Y ) (7)

where H(X) is the entropy of X . The entropy is de-

ﬁned for a continuous random variable as:

H(X) = −

(ζ

)log f

(ζ

) dζ

(8)

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

where f

is the probability density function (pdf) of

X. The mutual information can then be rewritten as

I(X ;Y ) =

Z Z

X,Y

(ζ

,ζ

)log

X,Y

(ζ

,ζ

)

(ζ

) f

(ζ

)

dζ

(9)

Unfortunately in practice neither f

, f

nor f

X,Y

are known. The MI cannot thus be directly computed;

it has to be estimated from the available samples.

Several methods have been proposed for this task,

including a histogram based estimator (Moddemei-

jer, 1989), a Parzen-window based estimator (Steuer

et al., 2002) and a k-NN based estimator (Gomez-

Verdejo et al., 2009).

3 METHODOLOGY

Previous work on inter-patient heart beat classiﬁca-

tion use features extracted from the heart beat signal

using either a priori knowledge or by comparing sev-

eral combinations of feature sets. There is thus a lack

of assessment of the relevance of indivual features.

In this work, two feature selection techniques are in-

vestigated to select the individual features serving the

classiﬁcation task. A large number of features are

considered and compared on a fair basis. This section

introduces the methodology followed in our experi-

ments.

3.1 ECG Data

The standard MIT-BIH arrhythmia database (Gold-

berger et al., 2000) is used in the experiments. It

contains 48 half-hour long ambulatory recordings ob-

tained from 48 patients, for a total of approximatively

110’000 heart beats manually labeled into 15 distinct

beat types. According to the AAMI standards, the

four recordings including paced beats are rejected for

a total of 44 experimental recordings (Association for

the Advancement of Medical Instrumentation, 1998).

For each recording, two signals from two distinct

leads are available. The sampled ECG signals are

ﬁrst ﬁltered using the same ﬁltering procedure as in

(Chazal et al., 2004; Park et al., 2008; De Lannoy

et al., 2010) to remove unwanted artifacts such as

baseline wanderings due to respiration, powerline in-

terference and other high frequency artifacts.

The 44 available recordings are divided in two

independent datasets of 22 recordings each with ap-

proximatively the same ratio of heart beats classes

(Chazal et al., 2004). The ﬁrst dataset is the train-

ing set, and is used to build the model. The second

dataset is the test set, and is used to obtain an inde-

pendent measure of the performances of the classiﬁer.

The R spike annotations provided with the

database are used as a marker to separate and iden-

tify the beats. The MIT-BIH heart beat labeled types

are then grouped according to the AAMI recommen-

dations into four more clinically relevant heart beat

classes (see Tab. 1 for grouping details). Table 2

shows the number of beats in each class and their fre-

quencies in the two datasets.

3.2 Feature Extraction

The popular feature groups previously proposed for

heart beat classiﬁcation are extracted from the heart

beat time series: R-R intervals (used in almost all

previous works), segmentation intervals (Christov

et al., 2006; Chazal et al., 2004), morphological fea-

tures (Chazal et al., 2004; Melgani and Bazi, 2008),

Hermite basis function expansion coefﬁcients (HBF)

(Lagerholm et al., 2000; Osowski et al., 2004; Park

et al., 2008) and higher order statistics (Osowski and

Hoai, 2001; Park et al., 2008). The following of this

section describes the features included in each of the

groups.

1. Segmentation Intervals (24 Features). The

ECG characteristic points, corresponding to the

onset and offset of P, QRS and T waves, are an-

notated using the standard ecgpuwave

segmenta-

tion software provided with the MIT-BIH arrhyth-

mia database. A large variety of 24 features are

then computed from the annotated characteristic

waves:

(a) QRS wave: ﬂag, area, maximum, minimum,

positive area, negative area, standard devia-

tion, skewness, kurtosis, length, QR length, RS

length;

(b) P wave: ﬂag, area, maximum, minimum,

length;

length, QT length, ST length.

When the characteristic points needed to compute

a feature failed to be detected in the heart beat an-

notation step, the feature value is set to the pa-

tient’s mean feature value.

2. R-R Intervals (8 Features). This group consists

of four features built from the original R spike an-

notations provided with the MIT-BIH database;

the previous R-R interval, the next R-R interval,

See http://www.physionet.org/physiotools/software-

index.shtml

FEATURE SELECTION FOR INTER-PATIENT SUPERVISED HEART BEAT CLASSIFICATION

Table 1: Grouping of the MIT-BIH labeled heart beat types according to the AAMI standards.

Normal beats (N) Supraventricular ectopic

beats (S)

Ventricular ectopic beats

(V)

Fusion beats (F)

Normal beats Atrial premature beat Premature ventricular

contraction

Fusion of ventricular and

normal beats

Left bundle branch block

beats

Aberrated atrial prema-

ture beat

Ventricular escape beats

Right bundle branch

block beats

Nodal (junctional) pre-

mature beats

Atrial escape beats Supraventricular prema-

ture beats

Nodal (junctional) es-

pace beats

Table 2: Distribution of heart beat classes in the two independent datasets.

N S V F Total

Training 45809 942 3784 413 50948

89.91% 1.85% 7.43% 0.81% 100%

Test 44099 1836 3219 388 49542

89.01% 3.71% 6.50% 0.78% 100%

the average R-R interval in a window of 10 sur-

rouding R spikes and the signal mean R-R inter-

val. The same four features are also computed us-

ing the R spikes detected by the annotation algo-

rithm.

3. Morphological Features (19 Features). Ten fea-

tures are derived by uniformly sampling the ECG

amplitude in a window deﬁned by the onset and

offset of the QRS complex, and nine other fea-

tures in a window deﬁned by the QRS offset and

the T-wave offset. As the ECG signals were al-

ready sampled, linear interpolation was used to

estimate the intermediate values of the ECG am-

plitude. Here again, when the onset or offset

points needed to compute a feature were not de-

tected, the feature value is set to the patient’s mean

feature value.

4. HBF Coefﬁcients (20 Features). The parameters

for computing the HBF expansion coefﬁcients as

deﬁned in (Park et al., 2008) are used. The order

of the Hermite polynomial is set to 20, and the

width parameter σ is estimated so as to minimize

the reconstruction error for each beat.

5. Higher Order Statistics (30 Features). The 2nd,

3rd and 4th order cumulant functions are com-

puted. The parameters as deﬁned in (Osowski

et al., 2004) are used: the lag parameters range

from -250 msec to 250 msec centered on the R

spike and 10 equally spaced sample points of each

cumulant function are used as features, for a total

of 30 features.

6. Normalized R-R Intervals (6 Features). These

features correspond to the same features as in the

R-R interval group except that they are normal-

ized by their mean value for each patient. These

features are thus independent from the mean nor-

mal behavior of the heart of patients, which can

naturally be very different between individuals,

possibly misleading the classiﬁer.

7. Normalized Segmentation Intervals (21 Fea-

tures). This group contains the same features

as in the segmentation group, except that they

are normalized by their mean value for each pa-

tient. The normalization is obviously not applied

to boolean segmentation features. Here again,

the objective is to make each feature independent

from the mean behavior of the heart of a patient,

because it can naturally be very different between

individuals.

Several studies have shown that using the infor-

mation from both leads can increase the classiﬁcation

performances (Chazal et al., 2004; Llamedo-Soria

and Martinez, 2007); all features are therefore com-

puted independently on both leads (except the four R-

R intervals and the three normalized reference R-R in-

tervals computed from original annotations which are

common to both leads), for a total of 249 individual

features.

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

3.3 Feature Selection

Feature selection can be achieved either by wrap-

per or ﬁlter approaches. The exhaustive wrapper ap-

proach consists in feeding a model with the 2

N−1

pos-

sible feature subsets (N being the total number of fea-

tures) and to choose the one for which the model per-

forms the best. The exhaustive wrapper approach is

therefore the optimal feature selection technique for

a given model. However, such an exhaustive search

is untractable in practice since it would require the

training (including the time-consuming optimization

of potential hyper-parameters) of 2

N−1

different mod-

els.

When simple and fast (e.g. linear) models are con-

sidered, one can nevertheless circumvent this issue by

using an incremental wrapper approach. One of the

most common incremental search procedures is the

forward selection algorithm. Its principle is to select

at each step the feature whose addition to the current

subset leads to the highest increase in prediction per-

formances. More precisely, the procedure usually be-

gins with the empty set of features. The ﬁrst selected

feature is then the one which individually maximises

the performances of the model. The second step con-

sists in ﬁnding the feature from the feature set which

leads to the best increase in performance when com-

bined to the previously selected feature. The proce-

dure is repeated until no feature can increase the per-

formance anymore.

Although this incremental search is not guaranted

to converge to the selection of the optimal subset of

features, it has been proven to be very efﬁcient in

practice and reduces the required number of models

to train from 2

N−1

to O(N). Since the training of the

weighted LDA model does not require the estimation

of any hyper-parameter and has a closed-form solu-

tion, a wrapper algorithm based on a forward search

strategy can be used for the weighted LDA classiﬁer.

Wrapper approaches, when affordable, are often pref-

ered to ﬁlter approaches because they are expected to

produce better results since they are designed for a

speciﬁc model.

On the other hand, when it is not affordable to

train tens or hundreds of prediction models, feature

selection should rather be achieved by the ﬁlter ap-

proach. Filter approaches are based on a criterion in-

dependent of the performances of the model. Those

methods are thus much faster than wrapper proce-

dures and are well suited in conjunction with more

sophisticated (i.e. non-linear) models. For example,

if the one-against-one approach is used for the multi-

class weighted SVM classiﬁer, N ∗ (N −1)/2 models

must be trained for one choice of features and each

model itself requires the tuning of two hyper-

parameters by cross-validation. In such situations,

even an incremental wrapper approach would be in-

tractable and a ﬁlter strategy must therefore be con-

sidered.

Since MI is able to detect relationships between

random variables and is naturally suitable for multi-

class problems, it is a powerful criterion for ﬁlter pro-

cedures. However, MI can detect non-linear relation-

ships and a linear classiﬁer using the given features

could possibly fail in grasping the required non-linear

dicriminative information. For this reason, only the

weighted SVM model with a non-linear kernel should

be tested on the variables selected by the MI ranking

procedure.

4 EXPERIMENTS AND RESULTS

For the reasons detailed in Section 3.3, two distinct

approaches to the feature selection problem are fol-

lowed, depending on the complexity of the classiﬁca-

tion model employed: a wrapper procedure with the

weighted LDA model using a forward search strat-

egy and a ranking procedure with the weighted SVM

model using the MI criterion. As in heart beat clas-

siﬁcation problems around 90% of data points corre-

spond to normal beats, a trivial model always predict-

ing the normal class would reach an accuracy of 90%.

The accuracy itself is thus not well suited for this

problem and the balanced classiﬁcation rate (BCR)

is rather considered in this work (De Lannoy et al.,

2010). According to preliminary experiments and ex-

pert opinions, the maximum number of allowed fea-

tures is arbitrarily set to 10.

For the weighted LDA model, the weights are set

to the same values as in (Chazal et al., 2004). The

forward selection is performed on the training set and

the BCR obtained at each step on both the test set and

the training set is shown in Fig. 1. Altough a BCR of

more than 80% can be reached on the training set, the

best performance achieved on the test set is a BCR of

73% with only two features.

As far as the weighted SVM model is considered,

the one-against-one approach is used for multi-class

classiﬁcation and the polynomial kernel is used to

achieve non-linear predictions. The weights for the

class imbalance in the cost function are set to the same

values as in (De Lannoy et al., 2010). A leave-one-

patient-out cross-validation procedure is used on the

training set to ﬁnd the best regularization and kernel

parameter values. The MI value between each feature

and the class labels is computed using a histogram-

based estimator (Moddemeijer, 1989) on the training

FEATURE SELECTION FOR INTER-PATIENT SUPERVISED HEART BEAT CLASSIFICATION

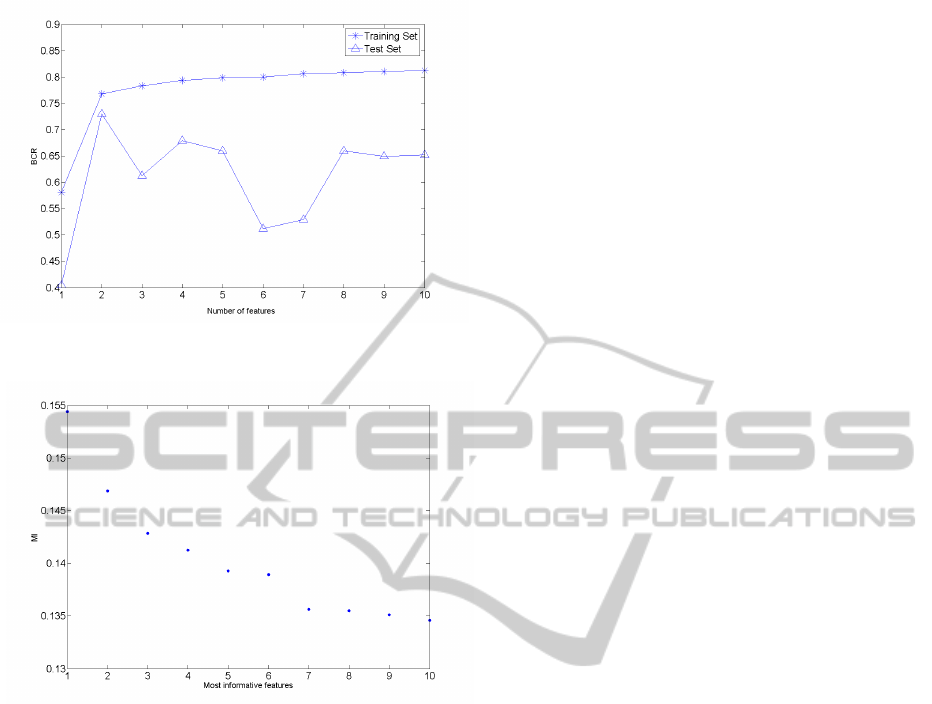
Figure 1: BCR obtained with the LDA and a forward wrap-

per feature selection procedure.

Figure 2: MI of the ten most informative features with the

class labels.

set to score the features.

It is important to note that unlike the correlation,

the MI is not bounded and the choice of the sig-

niﬁcantly informative features is not straightforward

(Steuer et al., 2002). For this reason, and in order to

keep the computational time reasonable, the number

of features is chosen by looking at the sorted MI val-

ues for the 10 most informative features as shown in

Fig. 2. It can observed in Fig. 2 that a number of six

features seems to be a good choice.

Table 3 summarizes the performances achieved by

the two feature selection approaches together with the

performances obtained with previously reported fea-

ture choices for the same models. The classiﬁcation

accuracy for each class is presented, together with the

BCR.

The results in Tab. 3 show that performing feature

selection is of great importance, since the weighted

SVM with only 6 features signiﬁcantly outperforms

all other classiﬁcation procedures with up to 50 fea-

tures. As far as linear classiﬁcation is concerned, an

improvement of less than 1% of BCR can be achieved

by using 50 features instead of only the 2 features se-

lected by the wrapper method.

From the 6 features selected with the MI criterion,

the ﬁrst one is the normalized previous R-R interval,

the second one is the normalized height of the T-wave

and the last four ones are high-order statistics. This is

in accordance with (De Lannoy et al., 2010), were the

best performances are obtained using R-R, normal-

ized R-R and HOS feature sets and the second best

performances with normalized interval features.

It is important to note that the performances re-

ported in Tab. 3 are different to the ones published in

(Chazal et al., 2004) and in (De Lannoy et al., 2010).

This can be explained by differences in methodolo-

gies. In (Chazal et al., 2004), the authors made a

tremendous work by manually correcting all the R

spike annotations. Since the R-R features are clearly

one of the most important features, this may explain

the differences in performances. However, manually

annotating all the signal is a time consuming pro-

cess which is not affordable in practice when thou-

sands of beats have to be evaluated. The difference

in performance with (De Lannoy et al., 2010) can

be explained by the fact that the authors select the

hyper-parameters of the SVM by measuring the per-

formances directly on the test set rather than a by us-

ing a cross-validation procedure on the training set

which is a less advantageous but more realistic situ-

ation.

5 CONCLUSIONS

The selection of discriminative features is of great im-

portance to help interpreting models and to increase

the performances by removing spurious features. In

this work, two feature selection strategies are evalu-

ated on real ambulatory recordings. The ﬁrst one is

a incremental wrapper procedure and the second one

is a ﬁlter approach. The wrapper is expected to per-

form better than the ﬁlter for a given model but re-

quires a large number of trainings. As a consequence,

it can only be affordable for models where no hyper-

parameter has to be tuned by cross-validation or for

models having a closed form training solution.

For this reason, the wrapper method is used with a

weighted LDA model using a forward search strategy.

Results show that the best performances on the test

set are obtained with only two features. These results

are similar to the performances of the same model us-

ing previously reported feature selection, where up to

50 features where required to attain the same perfor-

mances.

The ranking approach is used in conjunction with

BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing

Table 3: Classiﬁcation performances of the two feature selection methods compared to previously reported feature choices.

Model Feature selection Features BCR N S V F

wLDA Wrapper wLDA 2 73.00% 81.88% 70.53% 70.77% 68.81%

wLDA (Chazal et al., 2004) 50 73.83% 88.63% 44.66% 80.58% 81.44%

wSVM Ranking MI 6 82.99% 75.88% 82.63% 85.06% 88.40%

wSVM (De Lannoy et al., 2010) 36 71.55% 77.54% 42.86% 79.19% 86.60%

the weighted SVM classiﬁer and the MI criteria to

score the features. Six features are empirically se-

lected from the ranking results. Results with the

weighted SVM classiﬁer using only these 6 features

are signiﬁcantly higher than the performances with

the same model using previously reported feature

choices with up to 36 features. In particular, the accu-

racy for the S class is improved by almost 40%. The

six selected features are the normalized previous R-R

interval, the normalized height of the T-wave and four

high order statistics.

ACKNOWLEDGEMENTS

G. Doquire and G. de Lannoy are funded by a Belgian

F.R.I.A grant.

REFERENCES

Association for the Advancement of Medical Instrumenta-

tion (1998). Testing and reporting performance results

of cardiac rhythm and st segment measurement algo-

rithms. ANSI/AAMI EC38:1998.

Chazal, P. D., O’Dwyer, M., and Reilly, R. B. (2004). Auto-

matic classiﬁcation of heartbeats using ecg morphol-

ogy and heartbeat interval features. Biomedical Engi-

neering, IEEE Transactions on, 51:1196–1206.

Christov, I., G

omez-Herrero, G., Krasteva, V., Jekova, I.,

Gotchev, A., and Egiazarian, K. (2006). Comparative

study of morphological and time-frequency ecg de-

scriptors for heartbeat classiﬁcation. Med. Eng. Phys.,

28(9):876–887.

De Lannoy, G., Francois, D., Delbeke, J., and Verleysen, M.

(2010). Weighted svms and feature relevance assess-

ment in supervised heart beat classiﬁcation. Commu-

nications in Computer and Information Science (Se-

lected and extended papers of the BIOSIGNALS2010

conference), TO APPEAR.

Franc¸ois, D. (2008). Feature selection. In Wang, J., ed-

itor, Encyclopedia of data mining and warehousing,

second edition, Information Science Reference. Idea

Group Publishing.

Goldberger, A., Amaral, L., Glass, L., Hausdorff, J., Ivanov,

P. C., Mark, R., Mietus, J., Moody, G., Peng, C.-K.,

and Stanley, H. (2000). PhysioBank, PhysioToolkit,

and PhysioNet: Components of a new research re-

source for complex physiologic signals. Circulation,

101(23):e215–e220.

Gomez-Verdejo, V., Verleysen, M., and Fleury, J. (2009).

Information-theoretic feature selection for functional

data classiﬁcation. NEUROCOMPUTING, 72(16-18,

Sp. Iss. SI):3580–3589.

Lagerholm, M., Peterson, C., Braccini, G., Edenbrandt,

L., and Sornmo, L. (2000). Clustering ecg com-

plexes using hermite functions and self-organizing

maps. Biomedical Engineering, IEEE Transactions

on, 47(7):838–848.

Llamedo-Soria, M. and Martinez, J. (2007). An ecg classi-

ﬁcation model based on multilead wavelet transform

features”. In Computers in Cardiology, volume 35.

Melgani, F. and Bazi, Y. (2008). Classiﬁcation of electro-

cardiogram signals with support vector machines and

particle swarm optimization. Information Technology

in Biomedicine, IEEE Transactions on, 12(5):667–

677.

Moddemeijer, R. (1989). On estimation of entropy and mu-

tual information of continuous distributions. Signal

Processing, 16(3):233–246.

Nguyen, G. H., Bouzerdoum, A., and L., P. S. (2009).

Learning Pattern Classiﬁcation Tasks with Imbal-

anced Data Sets. INTECH.

Osowski, S. and Hoai, L. (2001). Ecg beat recognition us-

ing fuzzy hybrid neural network. Biomedical Engi-

neering, IEEE Transactions on, 48(11):1265–1271.

Osowski, S., Hoai, L., and Markiewicz, T. (2004). Sup-

port vector machine-based expert system for reliable

heartbeat recognition. Biomedical Engineering, IEEE

Transactions on, 51(4):582–589.

Park, K., Cho, B., Lee, D., Song, S., Lee, J., Chee, Y., Kim,

I., and Kim, S. (2008). Hierarchical support vector

machine based heartbeat classiﬁcation using higher

order statistics and hermite basis function. In Com-

puters in Cardiology, pages 229–232.

Shannon, C. E. (1948). A mathematical theory of com-

munication. Bell Systems Technical Journal, 27:379–

423,623–656.

Steuer, R., Kurths, J., Daub, C. O., Weise, J., and Selbig, J.

(2002). The mutual information: Detecting and eval-

uating dependencies between variables. Bioinformat-

ics, 18(suppl 2):S231–240.

FEATURE SELECTION FOR INTER-PATIENT SUPERVISED HEART BEAT CLASSIFICATION