
A PULSE WAVEFORM DATA DECOMPOSITION BASED ON
MULTI COMPONENT CURVE FIT COMPARED WITH SECOND
DERIVATIVE PHOTOPLETHYSMOGRAPHY AND PHASE
PLANE PLOT
M. Huotari
1
, K. Maatta
2
and J. Kostamovaara
2,3
Department of Electrical and Information Engineering,
1
Microelectronics and Materials Physics Laboratories
2
Electronics
Laboratory, University of Oulu, Pentti Kaiteran tie 1, FIN-90014 Oulu, Finland
3
Academy of Finland, PO Box 99, FIN-00501 Helsinki, Finland
Keywords: Pulse wave analysis, Photoplethysmography, Arterial stiffness, Lognormal function, Second derivative,
Phase plane plot.
Abstract: With a new photoplethysmographic (PPG) device we have been attending to photoplethysmographic signals
of different ages for signal decomposition purpose. Because PPG is a non-invasive, and easily attachable
measurement technique both suitable in health care applications we concentrated on its comprehensive
signal analysis and waveform interpretation. By means of PPG it is easy to capture data for further analysis.
In the world cardiovascular diseases are the frequent cause of death that’s why we are concern on
cardiovascular diseases. The main cause of incidents can be high arterial stiffness which is symptomless and
increases the risk as a function of age causing cardiovascular diseases. Arteries stiffen normally as a
consequence of age, but also because of insalubrious mores and many diseases. Normal age related stiffness
occurs when the elastic fibers within the arterial walls begin to weaken due to age, but diseases as
arteriosclerosis accelerate this process. However, we believe that it is possible to prevent arterial stiffening
if detected early enough. For this reason we have derived indexes to indicate a possible arterial stiffness
value..
1 INTRODUCTION
Many photoplethysmographic (PPG) devices exist,
but they are not practical and not accurate enough
for the purpose of the recent study. Infra red light
emitting diode (LED) is used as the light source as it
is cheap, small, secure to human eye and energy-
friendly.
Cardiovascular diseases or even arterial stiffness
does not cause any symptoms, but after the person
exercises the symptoms appear. During the first
symptoms 60% of the affected persons die. These
persons are and have been in danger for long time.
But measuring blood pressure is not enough,
because it do not see the arterial stiffness at all.
That’s why we have been developing an optical
device for arterial stiffness measurement and
software for analysis of the measurement results.
The extracted PPG pulse wave was evaluated by
a pulse waveform analysis for 10-20 s every single
pulse of the finger and toe records.
2 MATERIALS AND METHODS
The new PPG system consists of two optical
measurement probes, one for a finger and the other
for a toe, and a compound electronics unit for
handling the optically measured signals based on
phase sensitive detection (PSD). The measurement
head consists of two LEDs and one large area
semiconductor photo detector for collecting light
emitted by the LEDs through the finger or toe. The
compound electronic unit contains electronics for
driving the LEDs (940 nm), two preamplifiers for
signals, four PSD channels, an analog-to-digital
converter and an USB-interface for transferring the
digitized results onto a laptop. In addition, parallel
methods of electrocardiogram (ECG) and
phonocardiogram (PCG) have been measured
simultaneously to support the later PPG analyses.
The subjects were measured a.m. in supine position
without coffee or tobacco in the morning. Each
measurement took about five minutes to obtain
477
Huotari M., Maatta K. and Kostamovaara J..
A PULSE WAVEFORM DATA DECOMPOSITION BASED ON MULTI COMPONENT CURVE FIT COMPARED WITH SECOND DERIVATIVE
PHOTOPLETHYSMOGRAPHY AND PHASE PLANE PLOT.
DOI: 10.5220/0003163804770480
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), pages 477-480
ISBN: 978-989-8425-35-5
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
consecutive 300 pulses, of which parallel 10 to 20
most stable were selected for pulse wave
decomposition analysis.
In this research, the index
finger and index toe were always under
measurement. After measurements we depict the toe
PPG as a function of the finger PPG which describe
complex non-harmonic motion in all cases. The
phase shifts were apparent that delay semantics can
be difficult to define and used with a causal system
relations.
In the pulse wave decomposition analysis, each
pulse wave was divided into four lognormal wave
components. The compound decomposed
waveforms were after computation and fitting
visually compared to the original waves to make
sure the best fitting. This comparison and the four
lognormal functions can be used to obtain a residual
error curve and its chi-square value will describe the
goodness of the fit. The verification of multi-
lognormal functions can be justified as they well
represent the vascular network with many
asymmetric arterial double-branching and lognormal
distribution of the length of capillary arteries and
also the blood flow velocities in these capillaries
(Qian et al. 2000).
The Origin 7.5 (OriginLab
®) lognormal
procedure was utilized for analyzing the pulse waves
in time domain to obtain best mathematical fitting
with minimal residual error. In this procedure, the
Levenberg-Marquart algorithm (LMA) is a very
popular curve-fitting algorithm used in many
applications for solving non-linear curve-fitting
problems, e.g., logarithmic normal function curves.
LMA provides a numerical solution to the problem
of minimizing a function which can be nonlinear,
over a space of parameters of the function. In our
case we have selected four similar lognormal
components which have 4x3 parameters and the
requirement for the correlation coefficients (R
2
) to
be 0.995 or over. We used the peak time values of
the 1
st
and the 2
nd
lognormal function, called
percussion and tidal component to find out arterial
stiffness values for the population measurements.
We also determined the 2
nd
derivative function of the
PPG wave which contains the parameters a, b, c, d,
and e, respectively in each pulse wave. The second
derivative of the finger photoplethysmography
(SDPPG) has been applided as a rapid and
convenient method for pulse-wave inspection. The
determination of vascular aging is possible
throughout the SDPPG, but especially effective it is
through the third derivative of the finger PPG
(TDPPG). In the case of typical SDPPG waveform
were characteristic waves are missing, the TDPPG
can still more uncover the characteristic waves. PPG
waveforms are varied by very little with each
subject. Therefore there are some cases when
characteristic wave of PPG was not found by one
technique we selected another one. The derivatives
of waveforms are changed by the area, width and the
function’s peak value.
3 RESULTS AND DISCUSSION
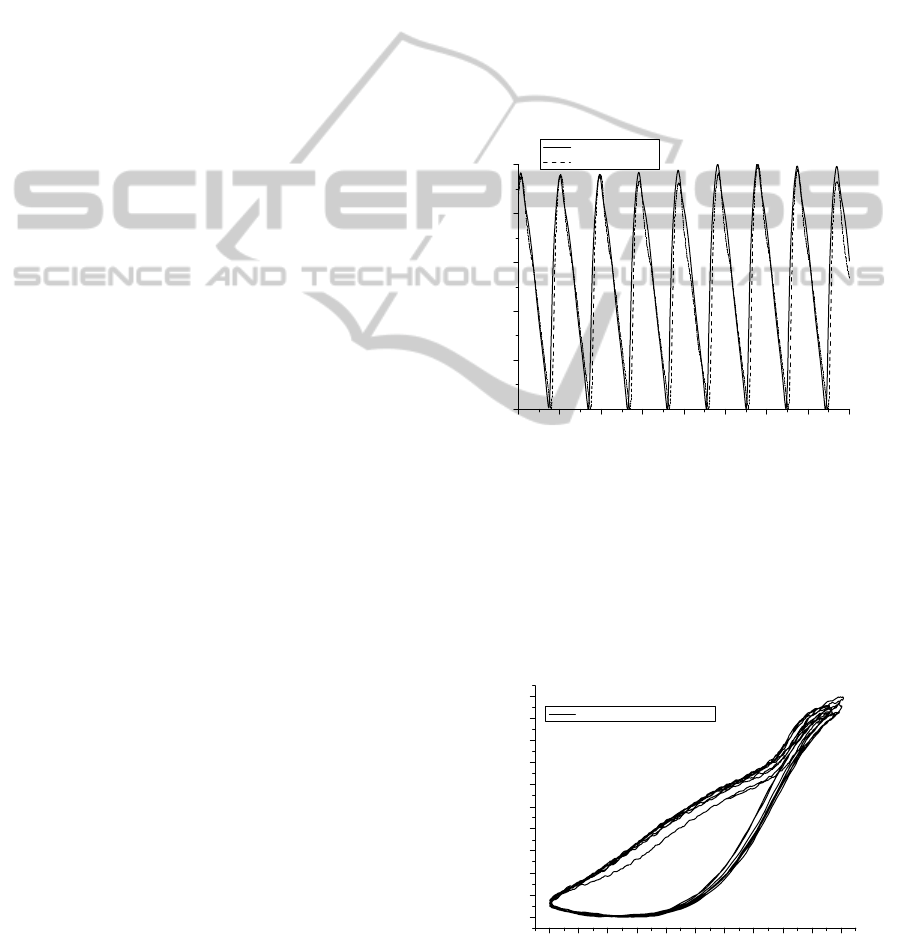
In Figure 1 it is shown as an example consecutive
PPG waveforms of the pulse wave signal at 940 nm
(IR) measured through the index finger tip pulse
wave (PPG1, straight) and the second toe tip (PPG2,
dash). Signals are normalized for the amplitude.
012345678
0,0
0,2
0,4
0,6
0,8
1,0
PPG
relative
t[s]
BTTL72_PPG1
D PPG2
Figure 1: The finger (straight) and toe (dash) PPG of a 72
years male person.
Figure 2 shows the causal relation between the
PPG1 and PPG2 in a phase plane, the PPG2 as a
function of the PPG1. When the PPG1 increases the
PPG2 still decreases, but after a certain value of the
PPG1 the PPG2 begins to increase. After the peak
value, the both signals decreases almost linearly to
the end of each pulse wave.
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
PPG2
rel
PPG1
rel
F TTLL72 PPG2 vs PPG1
Figure 2: PPG2 vs. PPG1 of the pulse waves in Figure 1.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
478

In Figure 3 it is illustrated an analyzed
compound finger PPG waveform. It contains the
typical PPG components. In this case the PPG
waveform analyses are covering the following four
pulse components in each pulse wave: percussion,
tidal, dichrotic, and peripheral reflection component.
Percussion is caused by the contraction of the heart
left ventricular muscle. The second component is the
tidal wave, occurring during the later part of the
systole, caused by the elastic properties of aorta. The
dichtrotic component is the reflected pulse from
lower periphery elasticity and vessel branching (A G
Scandurra et al. 2007).
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0,0
0,2
0,4
0,6
0,8
1,0
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
-0,050
-0,025
0,000
0,025
0,050
0,16221
0,27575
0,4704
0,71372
t
2
PPG1
rel
Residual error
t[s]
t´= t
2
-t
1
=0.05354s ; t´-t
1
= Δt= -0.10867s ; t
2
/t
1
=1.7000
Data: Data8_B
Model: LogNormal
Equation:
y = y0 + A/(sqrt(2*PI)*w*x)*exp(-(ln(x/xc))^2/(2*w^2))
Weighting:
y No weighting
Chi^2/DoF = 0.00037
R^2 = 0.99595
y0 0 ±0
xc1 0.27539 ±0.00779
w1 0.7163 ±0.0101
A1 0.29007 ±0.00777
xc2 0.28766 ±0.00337
w2 0.21826 ±0
A2 0.05006 ±0.00246
xc3 0.5124 ±0.00606
w3 0.26652 ±0.01688
A3 0.15757 ±0.00531
xc4 0.72135 ±0
w4 0.12946 ±0.01189
A4 0.02792 ±0.00522
t[s]
t
1
Figure 3: An analyzed finger PPG waveform which
contains the percussion component (green), the tidal
component (blue), the dicrotic component (magneta), and
the peripheral reflection component (navy). The lower part
of the figure shows the residual error and R
2
=0.99595.
5 101520253035404550556065707580
1,00
1,25
1,50
1,75
2,00
2,25
2,50
2,75
Linear Regression for Data2_B:
Y = A + B * X
Parameter Value Error
--------------------------------------------
A 2,341 0,09292
B -0,0123 0,00197
---------------------------------------------
RSDNP
-0,813 0,1797 22 <0.0001
B
Linear Fit of Data2_B
t
T
/t
P
age [years]
Figure 4: The tidal peak time divided by the percussion
peak time as a function of the age for 22 persons of
different ages (R=-0.813).
Figure 4 shows the tidal peak time divided by the
percussion peak time of each PPG waveform R=-
0.813 which is rather good correlation coefficient.
012345678
-0,5
-0,4
-0,3
-0,2
-0,1
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
0,14063
0,74805
0,92969
1,08398
1,70313
1,88281
2,04102
2,65625
2,81836
2,98633
3,61133
3,78906
3,94531
4,55469
4,73047
4,90625
5,51758
5,69531
5,85547
6,48242
6,6543
6,83008
7,4394
7,61914
7,77344
0,06055
0,82031
1,01367
1,77734
1,95898
2,73438
2,9043
3,68555
3,86133
4,63086
4,81836
5,59375
5,78125
6,55273
6,74219
7,51563
7,68945
e
d
c
b
d
2
PPG1/dt
2
t[s]
B TTLL72; d
2
PPG1/dt
2
a
Figure 5: The SDPPG waveform for the PPG1 in Figure 4.
The 2
nd
derivative of PPG1 contains the parameters a, b, c,
d, and e for each consecutive pulse wave. All peaks were
completely found in this case, but only marked for the first
pulse wave.
In Figure 5 it is shown a 2
nd
derivative of the
finger PPG waveform. They well hit into the search
window and all the peaks were found. However,
their biophysical meaning is open. It is known that
the components a, b c, and d belong to the first part
of systole, and e belongs to the late part of the
systole (J Hashimoto et al. 2002).
The characteristic points of the finger PPG can
be also extracted using the 3
rd
derivative PPG
(TDPPG) as shown in the Figure 6. The positions of
the peak of the percussion wave and the dicrotic
wave can be evaluated also from the inflection
points, where the third derivative of the PPG
changes sign, such as the zero crossing points.
0,0918
0,72656
0,84766
1,0332
1,68164
1,80859
2,00586
2,64063
2,75781
2,94922
3,59375
3,71094
3,91016
4,5332
4,65625
4,85352
5,49609
5,61914
5,8125
6,45898
6,58203
6,7793
7,4277
3
7,54102
7,72656
0,03906
0,77539
0,98242
1,72852
1,93945
2,67969
2,88477
3,63867
3,8418
4,58398
4,78711
5,54492
5,75
6,50977
6,7168
7,45898
7,66992
012345678
-30
-20
-10
0
10
20
30
TDPPG1
rel
t[s]
21 point S-G Derivative Smoothing of Data1_B TTLL72_TDPPG1
Figure 6: The TDPPG waveform for the PPG1 in Figure 1.
The 3
rd
derivative of PPG1 contains more clearly that the
SDPPG the similar parameters a, b, c, d, and e for each
consecutive pulse wave.
Figure 7 shows that the tidal peak times divided
by the percussion peak times of each PPG waveform
have clearly concentrated on the value 0.5 and the
A PULSE WAVEFORM DATA DECOMPOSITION BASED ON MULTI COMPONENT CURVE FIT COMPARED
WITH SECOND DERIVATIVE PHOTOPLETHYSMOGRAPHY AND PHASE PLANE PLOT
479
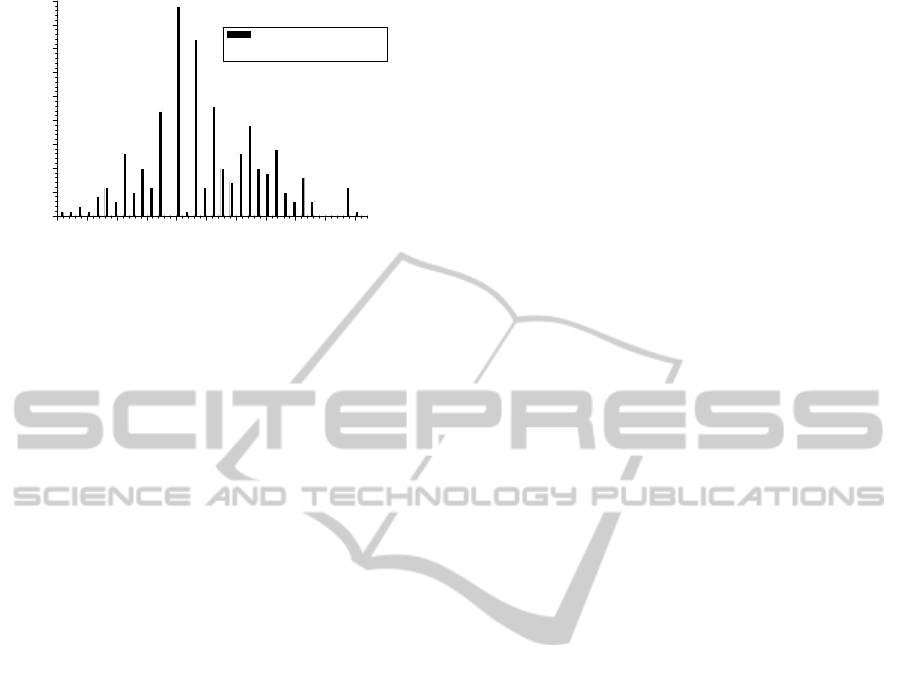
0,30 0,35 0,40 0,45 0,50 0,55 0,60 0,65 0,70 0,75 0,80
0
5
10
15
20
25
30
35
40
45
0.7143
0.46666
0.41666
0.53333
0.5625
0.62497
0.66668
Count
t
1
/t
2
Count 293 events of t
1
/t
2
as a functio of value t
1
/t
2
0.5
Figure 7: The percussion peak time divided by the tidal
peak time count as a function of the percussion peak time
divided by the tidal peak time for 293 events in 83 persons
of different ages. (see also Figure 3).
on some discrete values in 83 persons for 293 PPG
pulses.
This research studies the potential of PPG for
early diagnosis of arterial stiffness. PPG technology
is widely available at the pulse oxygen saturation
measurements and is relatively cheap and does not
require special expertise. PPG can be utilized for
detecting pulse waveforms. In the blood circulatory
system, the arterial pulse wave reflections depend on
the arterial wall stiffness. This study includes
creating a mathematical model for pulse wave-forms
for analyzing the four wave components of the
human pulse. This information based on the second
derivative photoplethysmogram can be further used
for estimating arterial stiffness which is normally
determined based on pulse wave velocity (A Qasem,
A Avolio 2008).
4 CONCLUSIONS
The location of a tidal wave seems to drift earlier by
the age, while the percussion wave drifts to the
opposite direction. By analyzing the four
components, one may be able to make conclusions
relating to arterial stiffness. It might be beneficial to
measure pulse waves instead of blood pressure due
to more information being available on the condition
of veins.The use of lagged gamma function might
also prove interesting (Qian et al. 2000).
Because the tidal peak time divided by the
percussion peak time of each PPG waveform (R=-
0.813) which is rather good correlation coefficient as
a function of age, this could be used as a measure of
arterial aging. The further investigation would be
warranted to see if a predictive index of blood
pressure changes might be obtained from pulse wave
analysis of PPG waveforms. The determination of
age-related changes in the arterial pulse wave by the
high fidelity PPG device, thus, provides important
supplementary information to that obtained by use of
the blood pressure measurements.
ACKNOWLEDGEMENTS
The research grant from the Finnish Cultural
Foundation is acknowledged for MH.
REFERENCES
H Qian, J. B. Bassingthwaighte (2000) A Class of Flow
Bifurcation Models with Lognormal Distribution and
Fractal Dispersion, Journal of theoretical Biology 205,
261-268.
A. G. Scandurra, G. J. Meschino, L. I. Passoni, A. L. Dai
Pra, A. R. Introzzi and F. M. Clara (2007)
Optimization of arterial age prediction models based
in pulse wave, Journal of Physics: Conference Series
90 012080.
J. Hashimoto et al. (2002) Pulse wave velocity and the
second derivative of the finger photoplethysmogram in
treated hypertensive patients: their relationship and
associating factors Journal of Hypertension, Vol 20
12; 2415-2422.
A. Qasem, A. Avolio (2008) Determination of aortic pulse
wave velocity from waveform decomposition of the
central aortic pressure pulse, Hypertension 51;188-
195.
BIOSIGNALS 2011 - International Conference on Bio-inspired Systems and Signal Processing
480
